1.1: Solving Linear Equations and Inequalities
- Page ID
- 48347
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Verify linear solutions.
- Use the properties of equality to solve basic linear equations.
- Clear fractions from equations.
- Identify linear inequalities and check solutions.
- Solve linear inequalities and express the solutions graphically on a number line and in interval notation.
Prerequisite Skills
Before you get started, take this prerequisite quiz.
1. Simplify \(2-6(4-7)^2\) without using a calculator.
- Click here to check your answer
-
\(-52\)
If you missed this problem, review here. (Note that this will open a different textbook in a new window.)
2. Evaluate \(6x−4\) when \(x=−2\).
- Click here to check your answer
-
\(-16\)
If you missed this problem, review here. (Note that this will open a different textbook in a new window.)
3. Evaluate \(-5x^2−x+9\) when \(x=-3\).
- Click here to check your answer
-
\(-33\)
If you missed this problem, review here. (Note that this will open a different textbook in a new window.)
4. Simplify \(7x−1−4x+5\).
- Click here to check your answer
-
\(3x+4\)
If you missed this problem, review here. (Note that this will open a different textbook in a new window.)
Solving Basic Linear Equations
An equation129 is a statement indicating that two algebraic expressions are equal. A linear equation with one variable130, \(x\), is an equation that can be written in the standard form \(ax + b = 0\) where \(a\) and \(b\) are real numbers and \(a ≠ 0\). For example
\(3 x - 12 = 0\)
A solution131 to a linear equation is any value that can replace the variable to produce a true statement. The variable in the linear equation \(3x − 12 = 0\) is \(x\) and the solution is \(x = 4\). To verify this, substitute the value \(4\) in for \(x\) and check that you obtain a true statement.
\(\begin{aligned} 3 x - 12 & = 0 \\ 3 ( \color{Cerulean}{4}\color{Black}{ )} - 12 & = 0 \\ 12 - 12 & = 0 \\ 0 & = 0 \:\: \color{Cerulean}{✓} \end{aligned}\)
Alternatively, when an equation is equal to a constant, we may verify a solution by substituting the value in for the variable and showing that the result is equal to that constant. In this sense, we say that solutions “satisfy the equation.”
Example \(\PageIndex{1}\):
Is \(a=2\) a solution to \(−10a+5=−25\)?
Solution
Recall that when evaluating expressions, it is a good practice to first replace all variables with parentheses, and then substitute the appropriate values. By making use of parentheses, we avoid some common errors when working the order of operations.
\(\begin{align*} - 10 a + 5 &= -25 \\ - 10 ( \color{Cerulean}{2} \color{Black}{ ) +} 5 & = -25 \\ -20 + 5 & = -25 \\ -15 &\neq 25\:\: \color{red}{✗}\end{align*}\)
Answer:
No, \(a=2\) does not satisfy the equation and is therefore not a solution.
Developing techniques for solving various algebraic equations is one of our main goals in algebra. This section reviews the basic techniques used for solving linear equations with one variable. We begin by defining equivalent equations132 as equations with the same solution set.
\(\left. \begin{aligned} 3 x - 5 & = 16 \\ 3 x & = 21 \\ x & = 7 \end{aligned} \right\} \quad \color{Cerulean}{Equivalent \:equations}\)
Here we can see that the three linear equations are equivalent because they share the same solution set, namely, \(\{7\}\). To obtain equivalent equations, use the following properties of equality133. Given algebraic expressions \(A\) and \(B\), where \(c\) is a nonzero number:
| Addition property of equality: | If \(A=B\), then \(A\color{Cerulean}{+c}\color{Black}{=} B\color{Cerulean}{+c}\) |
|---|---|
| Subtraction property of equality: | If \(A=B\), then \(A\color{Cerulean}{-c}\color{Black}{-}B\color{Cerulean}{-c}\) |
| Multiplication property of equality: | If \(A=B\), then \(\color{Cerulean}{c}\color{Black}{A}=\color{Cerulean}{c}\color{Black}{B}\) |
| Division property of equality: | If \(A=B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black}{=}\frac{B}{\color{Cerulean}{c}}\) |
Table 1.1.1
Note
Multiplying or dividing both sides of an equation by \(0\) is carefully avoided. Dividing by \(0\) is undefined and multiplying both sides by \(0\) results in the equation \(0 = 0\).
We solve algebraic equations by isolating the variable with a coefficient of 1. If given a linear equation of the form \(ax + b = c\), then we can solve it in two steps. First, use the appropriate equality property of addition or subtraction to isolate the variable term. Next, isolate the variable using the equality property of multiplication or division. Checking the solution in the following examples is left to the reader.
Example \(\PageIndex{2}\):
Solve: \(7x − 2 = 19\).
Solution
\(\begin{aligned} 7 x - 2 & = 19 \\ 7 x - 2 \color{Cerulean}{+ 2} & = 19 \color{Cerulean}{+ 2} & & \color{Cerulean}{Add\: 2\: to\: both\: sides.} \\ 7 x & = 21 \\ \frac { 7 x } { \color{Cerulean}{7} } & = \frac { 21 } { \color{Cerulean}{7} } & & \color{Cerulean}{Divide\: both\: sides\: by\: 7.} \\ x & = 3 \end{aligned}\)
Answer:
The solution is \(3\).
Example \(\PageIndex{3}\):
Solve: \(56 = 8 + 12y\).
Solution
When no sign precedes the term, it is understood to be positive. In other words, think of this as \(56 = +8 + 12y\). Therefore, we begin by subtracting \(8\) on both sides of the equal sign.
\(\begin{aligned} 56 \color{Cerulean}{- 8} & = 8 + 12 y \color{Cerulean}{- 8} \\ 48 & = 12 y \\ \frac { 48 } { \color{Cerulean}{12} } & = \frac { 12 y } { \color{Cerulean}{12} } \\ 4 & = y \end{aligned}\)
It does not matter on which side we choose to isolate the variable because the symmetric property134 states that \(4 = y\) is equivalent to \(y = 4\).
Answer:
The solution is \(4\).
Example \(\PageIndex{4}\):
Solve: \(\frac { 5 } { 3 } x + 2 = - 8\).
Solution
Isolate the variable term using the addition property of equality, and then multiply both sides of the equation by the reciprocal of the coefficient \(\frac{5}{3}\) .
\begin{aligned} \frac { 5 } { 3 } x + 2 & = - 8 \\ \frac { 5 } { 3 } x + 2 \color{Cerulean}{- 2} & = - 8 \color{Cerulean}{- 2}\quad \color{Cerulean}{Subtract\: 2\: on\: both\: sides.} \\ \frac { 5 } { 3 } x & = - 10 \\ \color{Cerulean}{\frac { 3 } { 5 }} \color{Black}{ \cdot} \frac { 5 } { 3 } x & = \color{Cerulean}{\frac { 3 } { \cancel{5} }} \color{Black}{\cdot} ( \overset{-2}{\cancel{-10}} )\quad \color{Cerulean}{Multiply \:both \:sides\: by\: \frac{3}{5}.} \\ 1x & = 3 \cdot ( - 2 ) \\ x & = - 6 \end{aligned}
Answer:
The solution is \(−6\).
In summary, to retain equivalent equations, we must perform the same operation on both sides of the equation.
Exercise \(\PageIndex{1}\)
Solve: \(\frac { 2 } { 3 } x + \frac { 1 } { 2 } = - \frac { 5 } { 6 }\).
- Answer
-
\(x=-2\)
Video Solution: www.youtube.com/v/cQwqXs9AD6M
General Guidelines for Solving Linear Equations
Typically linear equations are not given in standard form, and so solving them requires additional steps. When solving linear equations, the goal is to determine what value, if any, will produce a true statement when substituted in the original equation. Do this by isolating the variable using the following steps:
- Step 1: Simplify both sides of the equation using the order of operations and combine all like terms on the same side of the equal sign.
- Step 2: Use the appropriate properties of equality to combine like terms on opposite sides of the equal sign. The goal is to obtain the variable term on one side of the equation and the constant term on the other.
- Step 2a: Add or subtract as needed to isolate the variable.
- Step 2b: Divide or multiply as needed to isolate the variable.
- Step 3: Check to see if the answer solves the original equation.
We will often encounter linear equations where the expressions on each side of the equal sign can be simplified. If this is the case, then it is best to simplify each side first before solving. Normally this involves combining same-side like terms.
Note
At this point in our study of algebra the use of the properties of equality should seem routine. Therefore, displaying these steps in this text, usually in blue, becomes optional.
Example \(\PageIndex{5}\):
Solve: \(- 4 a + 2 - a = 1\).
Solution
First combine the like terms on the left side of the equal sign.
\(\begin{aligned} - 4 a + 2 - a = 1 & \quad \color{Cerulean}{ Combine\: same-side\: like\: terms.} \\ - 5 a + 2 = 1 & \quad\color{Cerulean} { Subtract\: 2\: on\: both\: sides.} \\ - 5 a = - 1 & \quad\color{Cerulean} { Divide\: both\: sides\: by\: - 5.} \\ a = \frac { - 1 } { - 5 } = \frac { 1 } { 5 } \end{aligned}\)
Always use the original equation to check to see if the solution is correct.
\(\begin{aligned} - 4 a + 2 - a & = - 4 \left( \color{OliveGreen}{\frac { 1 } { 5 }} \right) + 2 - \color{OliveGreen}{\frac { 1 } { 5 }} \\ & = - \frac { 4 } { 5 } + \frac { 2 } { 1 } \cdot \color{Cerulean}{\frac { 5 } { 5 }}\color{Black}{ -} \frac { 1 } { 5 } \\ & = \frac { - 4 + 10 + 1 } { 5 } \\ & = \frac { 5 } { 5 } = 1 \:\:\color{Cerulean}{✓} \end{aligned}\)
Answer:
The solution is \(\frac{1}{5}\) .
Given a linear equation in the form \(ax + b = cx + d\), we begin the solving process by combining like terms on opposite sides of the equal sign. To do this, use the addition or subtraction property of equality to place like terms on the same side so that they can be combined. In the examples that remain, the check is left to the reader.
Example \(\PageIndex{6}\):
Solve: \(−2y − 3 = 5y + 11\).
Solution
Subtract \(5y\) on both sides so that we can combine the terms involving y on the left side.
\(\begin{array} { c } { - 2 y - 3 \color{Cerulean}{- 5 y}\color{Black}{ =} 5 y + 11 \color{Cerulean}{- 5 y} } \\ { - 7 y - 3 = 11 } \end{array}\)
From here, solve using the techniques developed previously.
\(\begin{aligned} - 7 y - 3 & = 11 \quad\color{Cerulean}{Add\: 3\: to\: both\: sides.} \\ - 7 y & = 14 \\ y & = \frac { 14 } { - 7 } \quad\color{Cerulean}{Divide\: both\: sides\: by\: -7.} \\ y & = - 2 \end{aligned}\)
Answer:
The solution is \(−2\).
Solving will often require the application of the distributive property.
Example \(\PageIndex{7}\):
Solve: \(- \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x )\).
Solution
Simplify the linear expressions on either side of the equal sign first.
\(\begin{aligned} - \frac { 1 } { 2 } ( 10 x - 2 ) + 3 = 7 ( 1 - 2 x ) & \quad\color{Cerulean} { Distribute } \\ - 5 x + 1 + 3 = 7 - 14 x & \quad\color{Cerulean} { Combine\: same-side\: like\: terms. } \\ - 5 x + 4 = 7 - 14 x & \quad\color{Cerulean} { Combine\: opposite-side\: like\: terms. } \\ 9 x = 3 & \quad\color{Cerulean} { Solve. } \\ x = \frac { 3 } { 9 } = \frac { 1 } { 3 } \end{aligned}\)
Answer:
The solution is \(\frac{1}{3}\) .
Example \(\PageIndex{8}\):
Solve: \(5(3−a)−2(5−2a)=3\).
Solution
Begin by applying the distributive property.
\(\begin{aligned} 5 ( 3 - a ) - 2 ( 5 - 2 a ) & = 3 \\ 15 - 5 a - 10 + 4 a & = 3 \\ 5 - a & = 3 \\ - a & = - 2 \end{aligned}\)
Here we point out that \(−a\) is equivalent to \(−1a\); therefore, we choose to divide both sides of the equation by \(−1\).
\(\begin{array} { c } { - a = - 2 } \\ { \frac { - 1 a } { \color{Cerulean}{- 1} }\color{Black}{ =} \frac { - 2 } { \color{Cerulean}{- 1} } } \\ { a = 2 } \end{array}\)
Alternatively, we can multiply both sides of \(−a=−2\) by negative one and achieve the same result.
\(\begin{aligned} - a & = - 2 \\ \color{Cerulean}{( - 1 )}\color{Black}{ (} - a ) & = \color{Cerulean}{( - 1 )}\color{Black}{ (} - 2 ) \\ a & = 2 \end{aligned}\)
Answer:
The solution is \(2\).
Exercise \(\PageIndex{2}\)
Solve: \(6 - 3 ( 4 x - 1 ) = 4 x - 7\).
- Answer
-
\(x=1\)
Video Solution: www.youtube.com/v/NAIAZrFjU-o
The coefficients of linear equations may be any real number, even decimals and fractions. When this is the case it is possible to use the multiplication property of equality to clear the fractional coefficients and obtain integer coefficients in a single step. If given fractional coefficients, then multiply both sides of the equation by the least common multiple of the denominators (LCD).
Example \(\PageIndex{9}\):
Solve: \(\frac { 1 } { 3 } x + \frac { 1 } { 5 } = \frac { 1 } { 5 } x - 1\).
Solution
Clear the fractions by multiplying both sides by the least common multiple of the given denominators. In this case, it is the \(LCD (3, 5) = 15\).
\(\begin{aligned} \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 3 } x + \frac { 1 } { 5 } \right) & = \color{Cerulean}{15}\color{Black}{ \cdot} \left( \frac { 1 } { 5 } x - 1 \right) \quad \color{Cerulean}{Multiply\: both\: sides\: by\: 15.} \\ \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 3 } x + \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } & = \color{Cerulean}{15}\color{Black}{ \cdot} \frac { 1 } { 5 } x - \color{Cerulean}{15}\color{Black}{ \cdot} 1\quad\color{Cerulean}{Simplify.} \\ 5 x + 3 & = 3 x - 15\quad\quad\quad\color{Cerulean}{Solve.} \\ 2 x & = - 18 \\ x & = \frac { - 18 } { 2 } = - 9 \end{aligned}\)
Answer:
The solution is \(−9\).
It is important to know that this technique only works for equations. Do not try to clear fractions when simplifying expressions. As a reminder:
| Expression | Equation |
|---|---|
| \(\frac { 1 } { 2 } x + \frac { 5 } { 3 }\) | \(\frac { 1 } { 2 } x + \frac { 5 } { 3 }=0\) |
Table 1.1.2
We simplify expressions and solve equations. If you multiply an expression by \(6\), you will change the problem. However, if you multiply both sides of an equation by \(6\), you obtain an equivalent equation.
| Incorrect | Correct |
|---|---|
|
\( \frac { 1 } { 2 } x + \frac { 5 } { 3 }\) \(\begin{aligned} \neq & \color{red}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} \\ = & 3 x + 10 \quad \color{red}{✗} \end{aligned}\) |
\(\begin{aligned} \frac { 1 } { 2 } x + \frac { 5 } { 3 } & = 0 \\ \color{Cerulean}{6 \cdot}\color{Black}{ \left( \frac { 1 } { 2 } x + \frac { 5 } { 3 } \right)} & = \color{Cerulean}{6 \cdot}\color{Black}{ 0} \\ 3 x + 10 & = 0\quad\color{Cerulean}{✓} \end{aligned}\) |
Table 1.1.3
Applications Involving Linear Equations
Algebra simplifies the process of solving real-world problems. This is done by using letters to represent unknowns, restating problems in the form of equations, and by offering systematic techniques for solving those equations. To solve problems using algebra, first translate the wording of the problem into mathematical statements that describe the relationships between the given information and the unknowns. Usually, this translation to mathematical statements is the difficult step in the process. The key to the translation is to carefully read the problem and identify certain key words and phrases.
| Key Words | Translation |
|---|---|
| Sum, increased by, more than, plus, added to, total | \(+\) |
| Difference, decreased by, subtracted from, less, minus | \(-\) |
| Product, multiplied by, of times, twice | \(\cdot\) |
| Quotient, divided by, ratio, per | \(÷\) |
| Is, total, result | \(=\) |
Table 1.1.4
When translating sentences into mathematical statements, be sure to read the sentence several times and parse out the key words and phrases. It is important to first identify the variable, “let x represent…” and state in words what the unknown quantity is. This step not only makes our work more readable, but also forces us to think about what we are looking for.
Example \(\PageIndex{10}\):
When \(6\) is subtracted from twice the sum of a number and \(8\) the result is \(5\). Represent this as an algebraic equation and find the number.
Solution
Let n represent the unknown number.
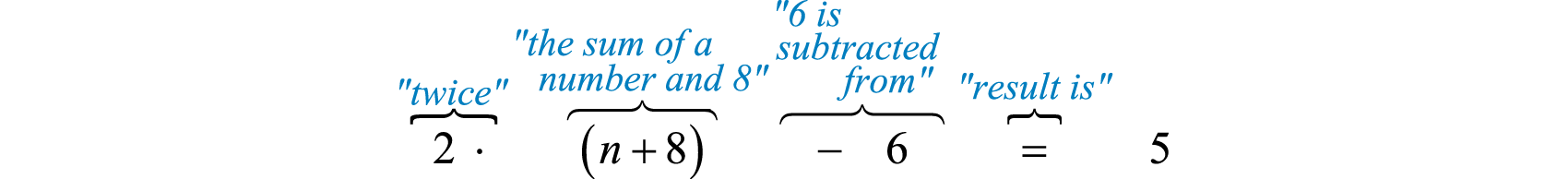
To understand why we included the parentheses in the set up, you must study the structure of the following two sentences and their translations:
|
“twice the sum of a number and 8” |
2(n+8) |
|
“the sum of twice a number and 8” |
2n+8 |
Table 1.1.5
The key was to focus on the phrase “twice the sum,” this prompted us to group the sum within parentheses and then multiply by \(2\). After translating the sentence into a mathematical statement we then solve.
\(\begin{aligned} 2 ( n + 8 ) - 6 & = 5 \\ 2 n + 16 - 6 & = 5 \\ 2 n + 10 & = 5 \\ 2 n & = - 5 \\ n & = \frac { - 5 } { 2 } \end{aligned}\)
Check.
\(\begin{aligned} 2 ( n + 8 ) - 6 & = 2 \left( \color{Cerulean}{- \frac { 5 } { 2 }}\color{Black}{ +} 8 \right) - 6 \\ & = 2 \left( \frac { 11 } { 2 } \right) - 6 \\ & = 11 - 6 \\ & = 5 \quad\color{Cerulean}{✓}\end{aligned}\)
Answer:
The number is \(−\frac{5}{2}\).
General guidelines for setting up and solving word problems follow.
- Step 1: Read the problem several times, identify the key words and phrases, and organize the given information.
- Step 2: Identify the variables by assigning a letter or expression to the unknown quantities.
- Step 3: Translate and set up an algebraic equation that models the problem.
- Step 4: Solve the resulting algebraic equation.
- Step 5: Finally, answer the question in sentence form and make sure it makes sense (check it).
For now, set up all of your equations using only one variable. Avoid two variables by looking for a relationship between the unknowns.
Linear Inequalities
A linear inequality138 is a mathematical statement that relates a linear expression as either less than or greater than another. The following are some examples of linear inequalities, all of which are solved in this section:
| \(5 x + 7 < 22\) | \(- 2 ( x + 8 ) + 6 \geq 20\) | \(- 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 )\) |
Table 1.1.5
A solution to a linear inequality139 is a real number that will produce a true statement when substituted for the variable.
Example \(\PageIndex{11}\):
Are \(x=−4\) and \(x=6\) solutions to \(5x+7<22\)?
Solution
Substitute the values in for \(x\), simplify, and check to see if we obtain a true statement.
|
Check \(x=−4\) |
Check \(x=6\) |
|---|---|
|
\(\begin{array} { r } { 5 ( \color{Cerulean}{- 4}\color{Black}{ )} + 7 < 22 } \\ { - 20 + 7 < 22 } \\ { - 13 < 22 } \:\:\color{Cerulean}{✓} \end{array}\) |
\(\begin{array} { c } { 5 ( \color{Cerulean}{6} \color{Black}{)} + 7 < 22 } \\ { 30 + 7 < 22 } \\ { 37 < 22 } \:\:\color{red}{✗} \end{array}\) |
Table 1.1.6
Answer:
\(x=−4\) is a solution and \(x=6\) is not
Linear inequalities have either infinitely many solutions or no solution. If there are infinitely many solutions, we graph the solution set on a number line and/or express the solution using interval notation.
Expressing Solutions to Linear Inequalities
What number would make the inequality \(x>3\) true? Are you thinking, "\(x\) could be four"? That’s correct, but \(x\) could be 6, too, or 137, or even 3.0001. Any number greater than three is a solution to the inequality \(x>3\). We show all the solutions to the inequality \(x>3\) on the number line by shading in all the numbers to the right of three, to show that all numbers greater than three are solutions. Because the number three itself is not a solution, we put an open parenthesis at three.
We can also represent inequalities using interval notation. There is no upper end to the solution to this inequality. In interval notation, we express \(x>3\) as \((3,\infty)\). The symbol \(\infty\) is read as “infinity.” It is not an actual number. Figure \(\PageIndex{2}\) shows both the number line and the interval notation.
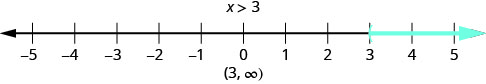
We use the left parenthesis symbol, (, to show that the endpoint of the inequality is not included. The left bracket symbol, [, would show that the endpoint is included.
The inequality \(x\leq 1\) means all numbers less than or equal to one. Here we need to show that one is a solution, too. We do that by putting a bracket at \(x=1\). We then shade in all the numbers to the left of one, to show that all numbers less than one are solutions (Figure \(\PageIndex{3}\)). There is no lower end to those numbers. We write \(x\leq 1x\leq 1 \)in interval notation as \((−\infty,1]\). The symbol \(−\infty\) is read as “negative infinity.”
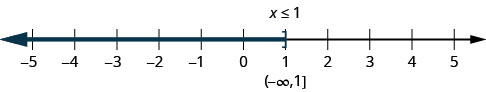
Figure \(\PageIndex{4}\) shows both the number line and interval notation.
INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

The notation for inequalities on a number line and in interval notation use the same symbols to express the endpoints of intervals. Notice that \(\infty\) and \(-\infty\) always use parentheses in interval notation, never brackets.
Example \(\PageIndex{12}\)
Graph each inequality on the number line and write in interval notation.
- \(x\geq −3\)
- \(x<2.5\)
- \(x\leq −\frac{3}{5}\)
- Answer
-
a.
\( x \geq -3 \) Shade to the right of \(−3\), and put a bracket at \(−3\). 
Write in interval notation. \( [-3, \infty) \) b.
\( x < 2.5 \) Shade to the left of 2.5 and put a parenthesis at 2.5. 
Write in interval notation. \( (-\infty, 2.5) \) c.
\( x \leq -\dfrac{3}{5} \) Shade to the left of \(−\frac{3}{5}\), and put a bracket at \(−\frac{3}{5}\). 
Write in interval notation. \( \bigg( -\infty, \dfrac{3}{5}\bigg] \)
Exercise \(\PageIndex{3}\)
Graph each inequality on the number line and write in interval notation:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<−\frac{2}{3}\).
- Answer
-
ⓐ
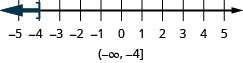
ⓑ

ⓒ
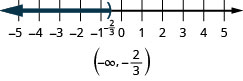
Solving Linear Inequalities
All but one of the techniques learned for solving linear equations apply to solving linear inequalities. You may add or subtract any real number to both sides of an inequality, and you may multiply or divide both sides by any positive real number to create equivalent inequalities. For example:
\[\begin{align*} 10 &> - 5 \\[4pt]
10{\color{Cerulean}{-7}}\,&{\color{Black}{>}} -5{\color{Cerulean}{-7}} & & {\color{Cerulean}{Subtract\: 7\: on\: both\: sides.}}\\[4pt]
3 &> - 12 & & \color{Cerulean}{✓}\quad\color{Cerulean}{True.} \\[20pt]
10 &>-5\\[4pt]
\frac{10}{\color{Cerulean}{5}}\,&\color{Black}{>}\frac{-5}{\color{Cerulean}{5}} & & \color{Cerulean}{Divide\: both\: sides\: by\: 5.}\\[4pt]
2 &>-1 & & \color{Cerulean}{✓\:\:True} \end{align*} \]
Subtracting \(7\) from each side and dividing each side by positive \(5\) results in an inequality that is true.
Example \(\PageIndex{13}\):
Solve and graph the solution set: \(5x+7<22\).
Solution
\(\begin{array} { c } { 5 x + 7 < 22 } \\ { 5 x + 7 \color{Cerulean}{- 7}\color{Black}{ < 22}\color{Cerulean}{ - 7} } \\ { 5 x < 15 } \\ { \frac { 5 x } {\color{Cerulean}{ 5} } < \frac { 15 } { \color{Cerulean}{5} } } \\ { x < 3 } \end{array}\)

It is helpful to take a minute and choose a few values in and out of the solution set, substitute them into the original inequality, and then verify the results. As indicated, you should expect \(x=0\) to solve the original inequality and that \(x=5\) should not.
|
Check \(x=0\) |
Check \(x=5\) |
|---|---|
|
\(\begin{array} { r } { 5 ( \color{Cerulean}{0}\color{Black}{ )} + 7 < 22 } \\ { 7 < 22 }\:\:\color{Cerulean}{✓} \end{array}\) |
\(\begin{array} { r } { 5 ( \color{Cerulean}{5}\color{Black}{ )} + 7 < 22 } \\ { 25 + 7 < 22 } \\ { 32 < 22 } \:\:\color{red}{✗} \end{array}\) |
Table 1.1.7
Checking in this manner gives us a good indication that we have solved the inequality correctly.
We can express this solution in two ways: using set notation and interval notation.
\(\begin{array} { r } { \{ x | x < 3 \} } &\color{Cerulean}{Set\: notation} \\ { ( - \infty , 3 ) } &\color{Cerulean}{Interval\: notation} \end{array}\)
In this text we will choose to present answers using interval notation.
Answer
\((−∞, 3) \)
When working with linear inequalities, a different rule applies when multiplying or dividing by a negative number. To illustrate the problem, consider the true statement \(10 > −5\) and divide both sides by \(−5\).
\(\begin{array} { l } { 10 > - 5 } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{>} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Divide\: both\: sides\: by\: -5.} \\ { - 2 \color{red}{>}\color{Black}{ 1} \quad \color{red}{✗} \color{Cerulean}{ False } } \end{array}\)
Dividing by \(−5\) results in a false statement. To retain a true statement, the inequality must be reversed.
\(\begin{array} { l } { 10 \color{OliveGreen}{>}\color{Black}{ - 5} } \\ { \frac { 10 } { \color{Cerulean}{- 5} } \color{Black}{<} \frac { - 5 } { \color{Cerulean}{- 5} } } \quad \color{Cerulean}{Reverse\: the\: inequality.} \\ { - 2 \color{OliveGreen}{<}\color{Black}{ 1} \quad \color{Cerulean}{✓} \color{Cerulean}{ True } } \end{array}\)
The same problem occurs when multiplying by a negative number. This leads to the following new rule: when multiplying or dividing by a negative number, reverse the inequality. It is easy to forget to do this so take special care to watch for negative coefficients. In general, given algebraic expressions \(A\) and \(B\), where \(c\) is a positive nonzero real number, we have the following properties of inequalities140:
| Addition property of inequalities: | If \(A<B\) then, \(A \color{Cerulean}{+c}\:\color{Black}{<}\:B\color{Cerulean}{+c}\) |
|---|---|
| Subtraction property of inequalities: | If \(A<B\) then, \(A \color{Cerulean}{-c}\:\color{Black}{<}\:B\color{Cerulean}{-c}\) |
| Multiplication property of inequalities: |
If \(A<B\), then \(\color{Cerulean}{c}\color{Black}{A}\:<\:\color{Cerulean}{c}\color{Cerulean}\color{Black}{B}\) If \(A<B\), then \(\color{Cerulean}{-c}\color{Black}{A}\:\color{OliveGreen}{>}\:\color{Cerulean}{-c}\color{Cerulean}\color{Black}{B}\) |
| Division property of inequalities: |
If \(A<B\), then \(\frac{A}{\color{Cerulean}{c}}\color{Black}{<}\frac{B}{\color{Cerulean}{c}}\) If \(A<B\), then \(\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\frac{\color{Black}{B}}{\color{Cerulean}{-c}}\) |
Table 1.1.8
We use these properties to obtain an equivalent inequality141, one with the same solution set, where the variable is isolated. The process is similar to solving linear equations.
Example \(\PageIndex{14}\):
Solve and graph the solution set: \(−2(x+8)+6≥20\).
Solution
\(\begin{aligned} - 2 ( x + 8 ) + 6 & \geq 20 \quad\color{Cerulean}{Distribute.} \\ - 2 x - 16 + 6 & \geq 20 \quad\color{Cerulean}{Combine\: like\: terms.} \\ - 2 x - 10 & \geq 20 \quad\color{Cerulean}{Solve\: for\: x.} \\ - 2 x & \geq 30 \quad\color{Cerulean}{Divide\: both\: sides\: by\: -2.} \\ \frac { - 2 x } { \color{Cerulean}{- 2} } & \color{OliveGreen}{\leq} \frac { \color{Black}{30} } { \color{Cerulean}{- 2} } \quad\color{Cerulean}{Reverse\: the\: inequality.} \\ x & \leq - 15 \end{aligned}\)
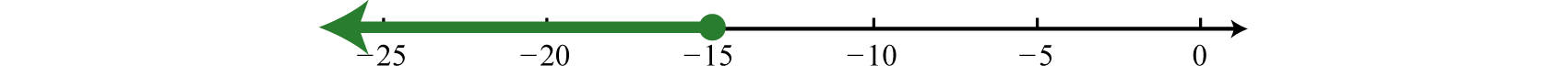
Answer:
Interval notation \((−∞, −15] \)
Example \(\PageIndex{15}\):
Solve and graph the solution set: \(−2(4x−5)<9−2(x−2)\).
Solution
\(\begin{array} { c } { - 2 ( 4 x - 5 ) < 9 - 2 ( x - 2 ) } \\ { - 8 x + 10 < 9 - 2 x + 4 } \\ { - 8 x + 10 < 13 - 2 x } \\ { - 6 x < 3 } \\ { \frac { - 6 x } { \color{Cerulean}{- 6} } \color{OliveGreen}{>} \frac { \color{Black}{3} } { \color{Cerulean}{- 6} } }\color{Cerulean}{Reverse\:the\:inequality.} \\ { x > - \frac { 1 } { 2 } } \end{array}\)

Answer:
Interval notation \((−\frac{1}{2}, ∞)\)
Example \(\PageIndex{16}\):
Solve and graph the solution set: \(\frac{1}{2}x−2≥\frac{1}{2}(\frac{7}{4}x−9)+1\).
Solution
\(\begin{array} { c } { \frac { 1 } { 2 } x - 2 \geq \frac { 1 } { 2 } \left( \frac { 7 } { 4 } x - 9 \right) + 1 } \\ { \frac { 1 } { 2 } x - 2 \geq \frac { 7 } { 8 } x - \frac { 9 } { 2 } + 1 } \\ { \frac { 1 } { 2 } x - \frac { 7 } { 8 } x \geq - \frac { 7 } { 2 } + 2 } \\ { - \frac { 3 } { 8 } x \geq - \frac { 3 } { 2 } } \\ { \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left(\color{Black}{ - \frac { 3 } { 8 } x} \right) \leq \left( \color{Cerulean}{- \frac { 8 } { 3 }} \right) \left( \color{Black}{-} \frac { 3 } { 2 } \right) \quad \color{Cerulean} { Reverse\: the\: inequality. } } \\ { x \leq 4 } \end{array}\)

Answer:
Interval notation: \((−∞, 4]\)
Exercise \(\PageIndex{4}\)
Solve and graph the solution set: \(10 - 5 ( 2 x + 3 ) \leq 25\)
- Answer
-
\([ - 3 , \infty )\);

Figure \(\PageIndex{9}\) Video Solution: www.youtube.com/v/COLLNtwYFm8
Translation of Linear Inequalities
Some of the key words and phrases that indicate inequalities are summarized below:
| Key Phrases | Translation |
|---|---|
| A number is at least \(5\). | \(x\geq 5\) |
| A number is \(5\) or more inclusive. | \(x\geq 5\) |
| A number is at most \(3\). | \(x\leq 3\) |
| A number is \(3\) or less inclusive. | \(x\leq 3\) |
| A number is strictly less than \(4\). | \(x<4\) |
| A number is less than \(4\), noninclusive. | \(x<4\) |
| A number is greater than \(7\). | \(x>7\) |
| A number is more than \(7\), noninclusive. | \(x>7\) |
| A number is in between \(2\) and \(10\). | \(2<x<10\) |
| A number is at least \(5\) and at most \(15\). | \(5\leq x\leq 15\) |
| A number may range from \(5\) to \(15\). | \(5\leq x\leq 15\) |
Table 1.1.9
Key Takeaways
- Solving general linear equations involves isolating the variable, with coefficient \(1\), on one side of the equal sign. To do this, first use the appropriate equality property of addition or subtraction to isolate the variable term on one side of the equal sign. Next, isolate the variable using the equality property of multiplication or division. Finally, check to verify that your solution solves the original equation.
- If solving a linear equation leads to a true statement like \(0 = 0\), then the equation is an identity and the solution set consists of all real numbers, \(ℝ\).
- If solving a linear equation leads to a false statement like \(0 = 5\), then the equation is a contradiction and there is no solution, \(Ø\).
- Clear fractions by multiplying both sides of an equation by the least common multiple of all the denominators. Distribute and multiply all terms by the LCD to obtain an equivalent equation with integer coefficients.
- Simplify the process of solving real-world problems by creating mathematical models that describe the relationship between unknowns. Use algebra to solve the resulting equations.
- Inequalities typically have infinitely many solutions. The solutions are presented graphically on a number line or using interval notation or both.
- All but one of the rules for solving linear inequalities are the same as solving linear equations. If you divide or multiply an inequality by a negative number, reverse the inequality to obtain an equivalent inequality.
Footnotes
129Statement indicating that two algebraic expressions are equal.
130An equation that can be written in the standard form \(ax + b = 0\), where \(a\) and \(b\) are real numbers and \(a ≠ 0\).
131Any value that can replace the variable in an equation to produce a true statement.
132Equations with the same solution set.
133Properties that allow us to obtain equivalent equations by adding, subtracting, multiplying, and dividing both sides of an equation by nonzero real numbers.
134Allows you to solve for the variable on either side of the equal sign, because \(x = 5\) is equivalent to \(5 = x\).
135Equations that are true for particular values.
136An equation that is true for all possible values.
137An equation that is never true and has no solution.

