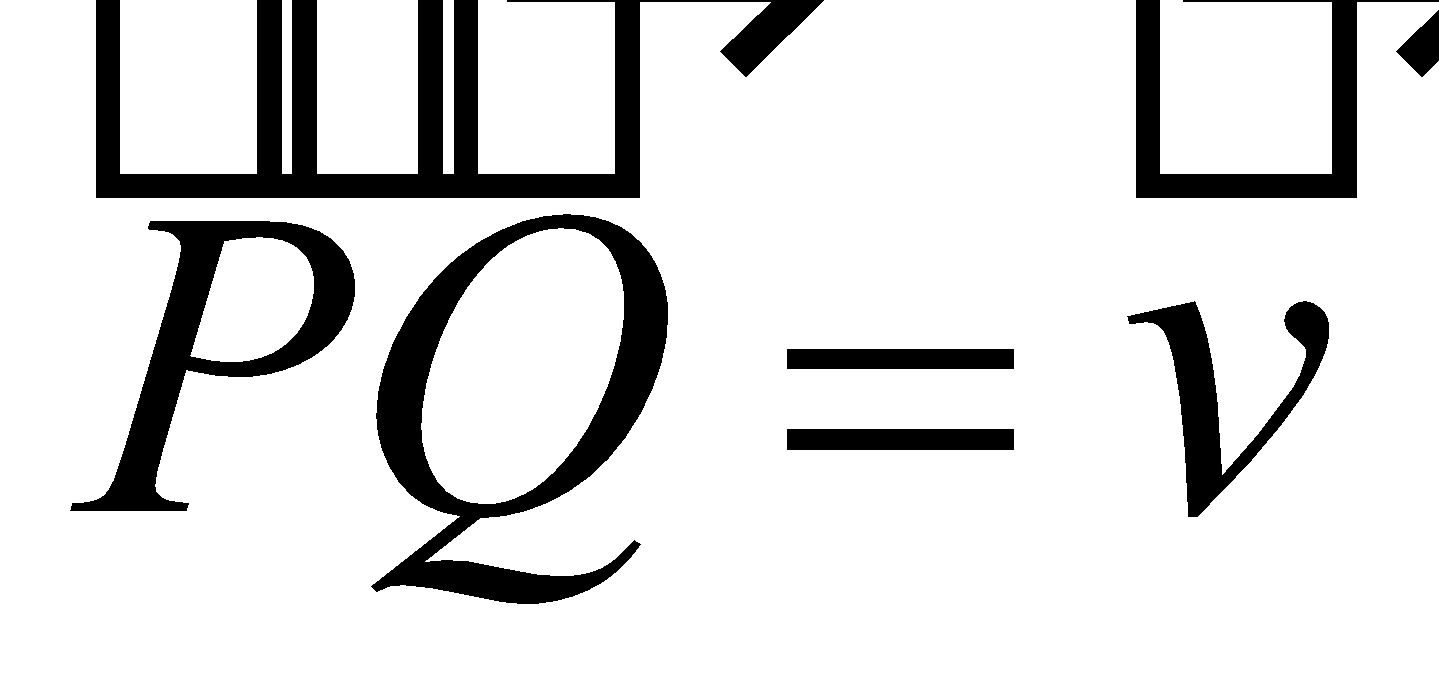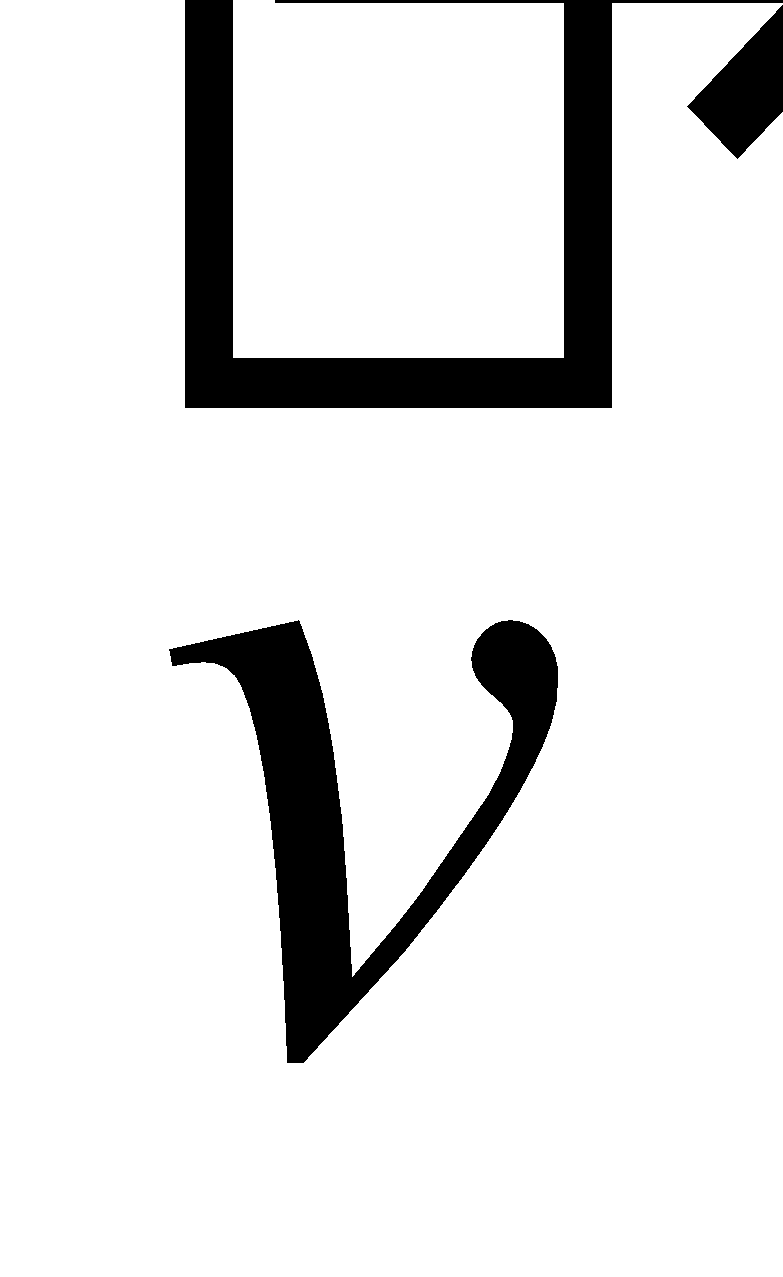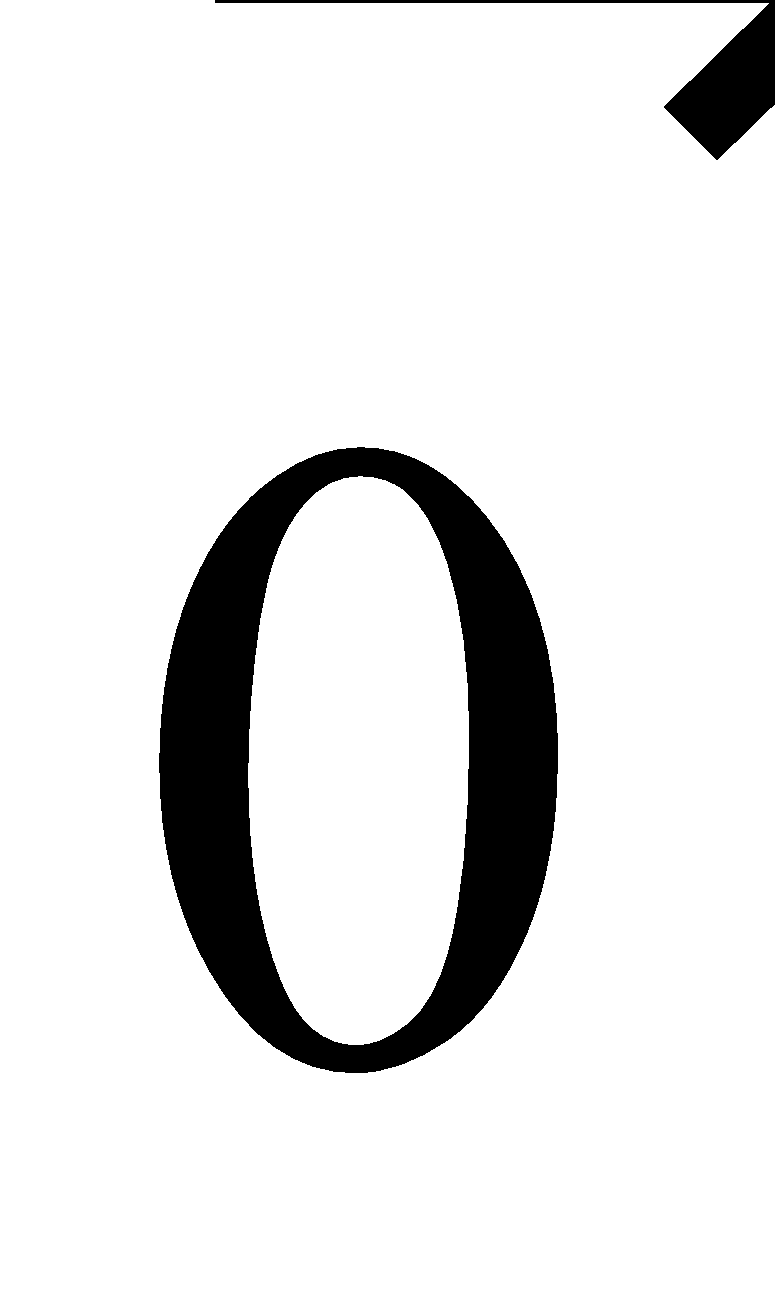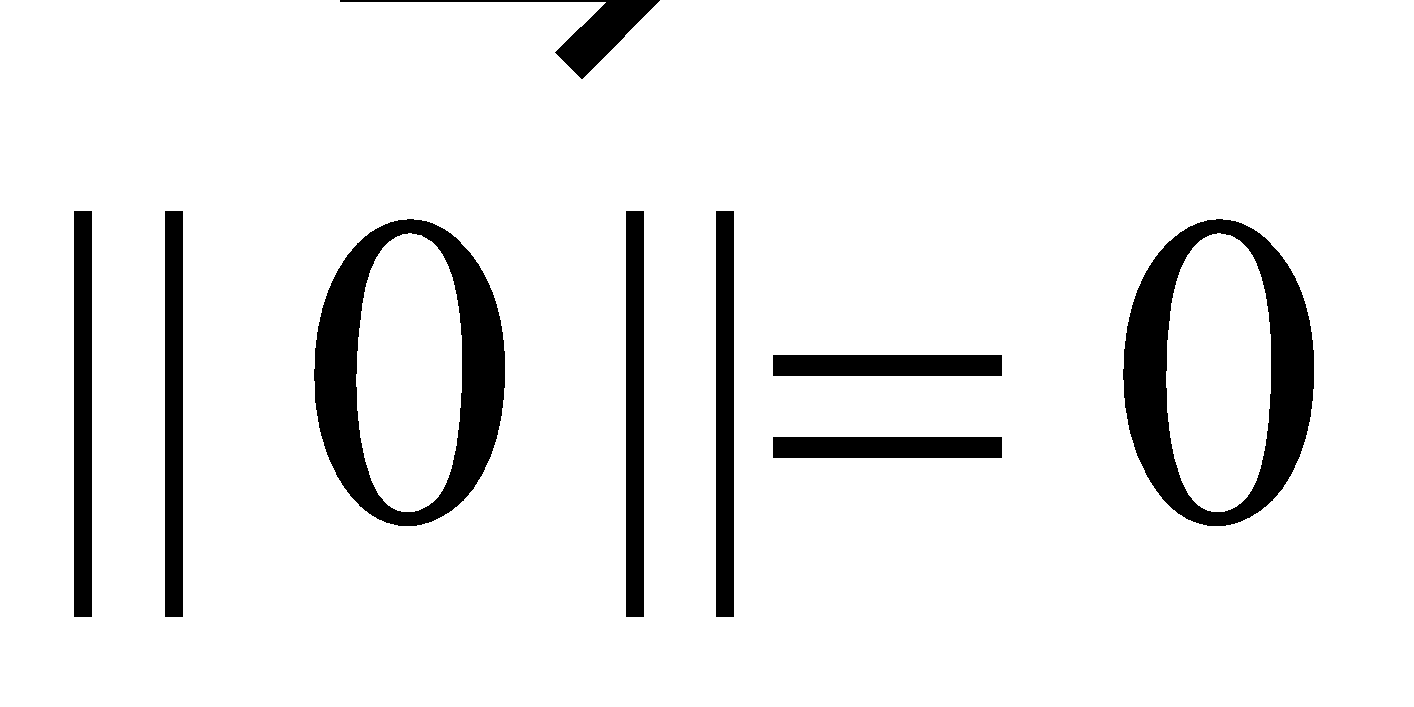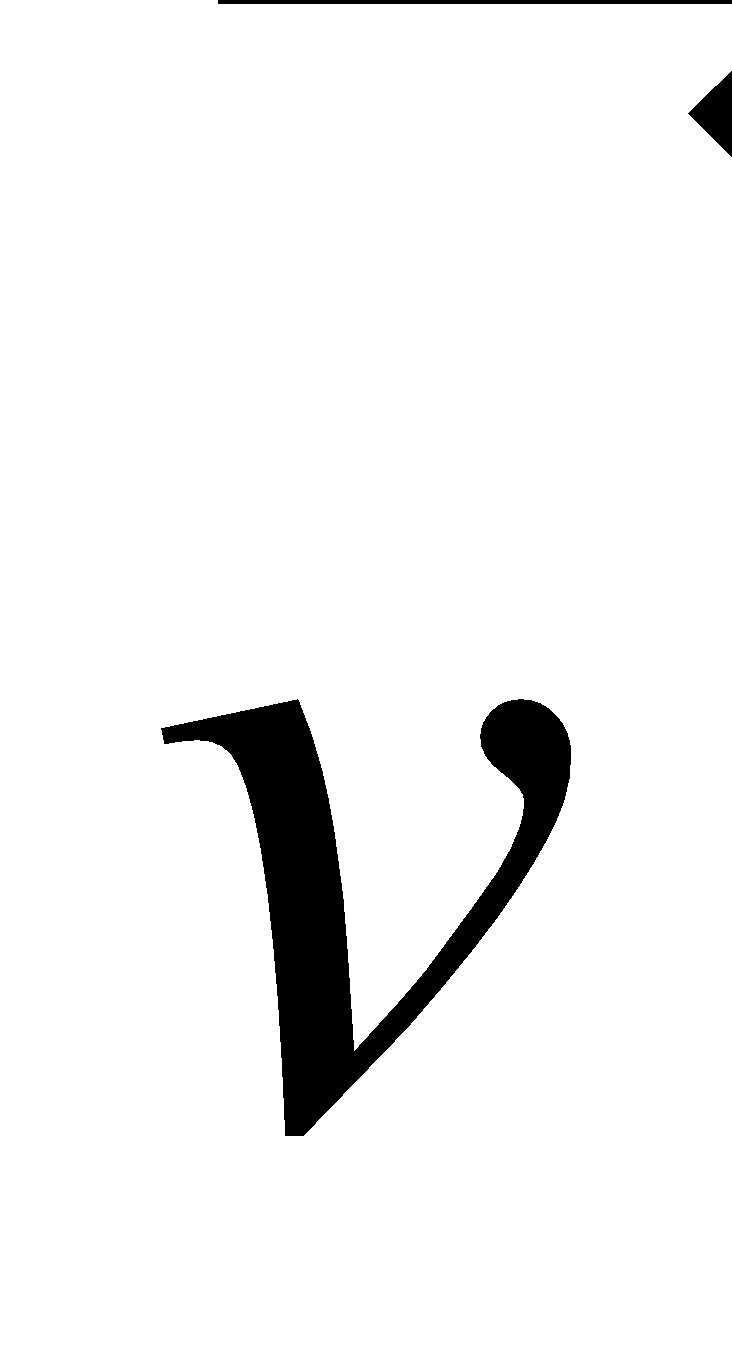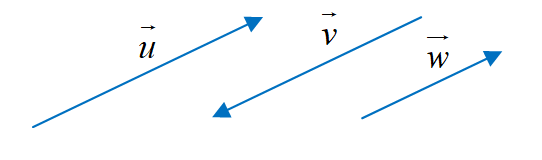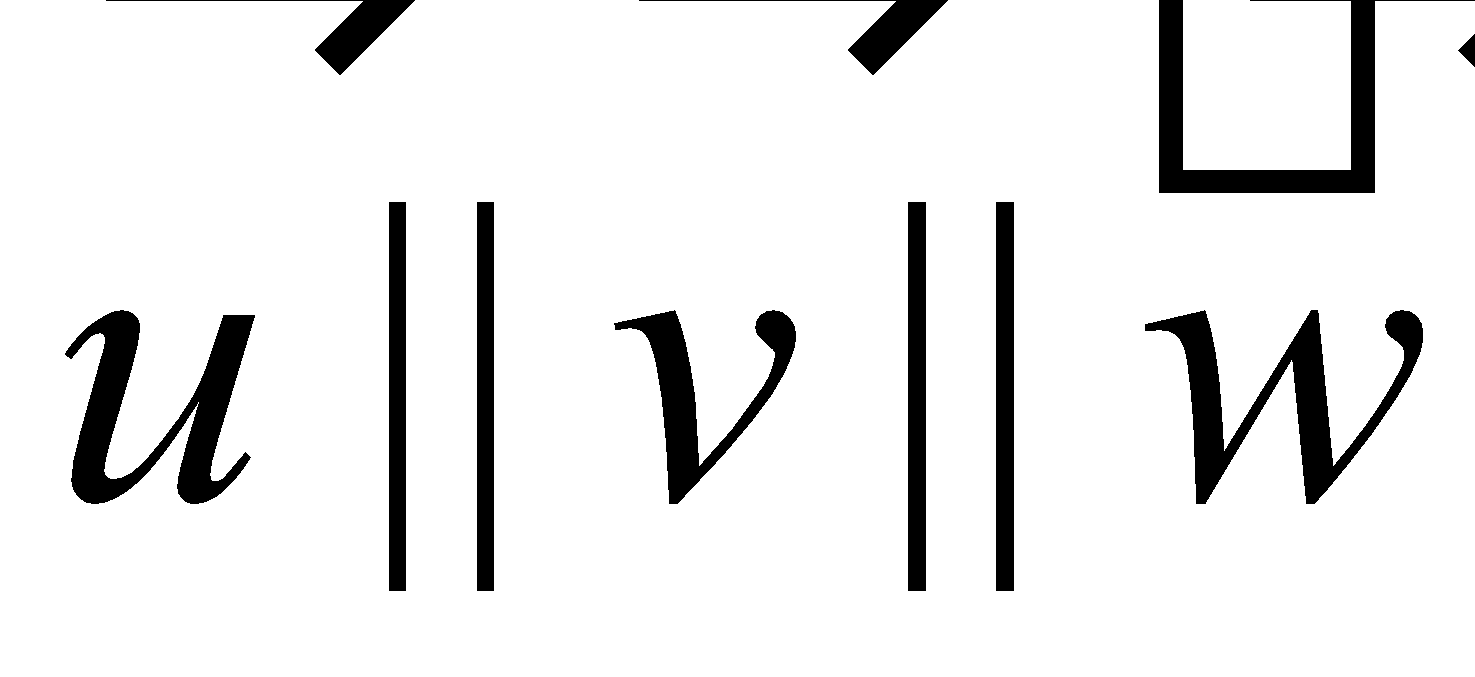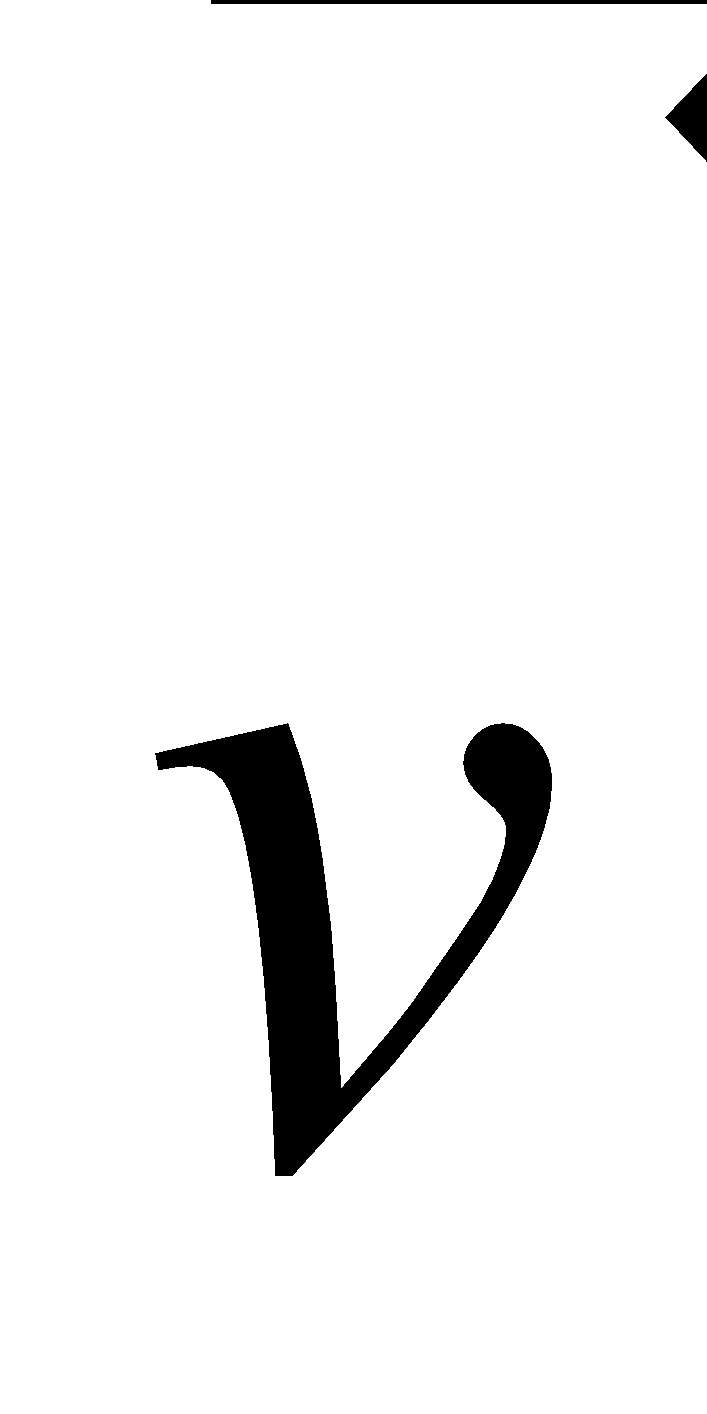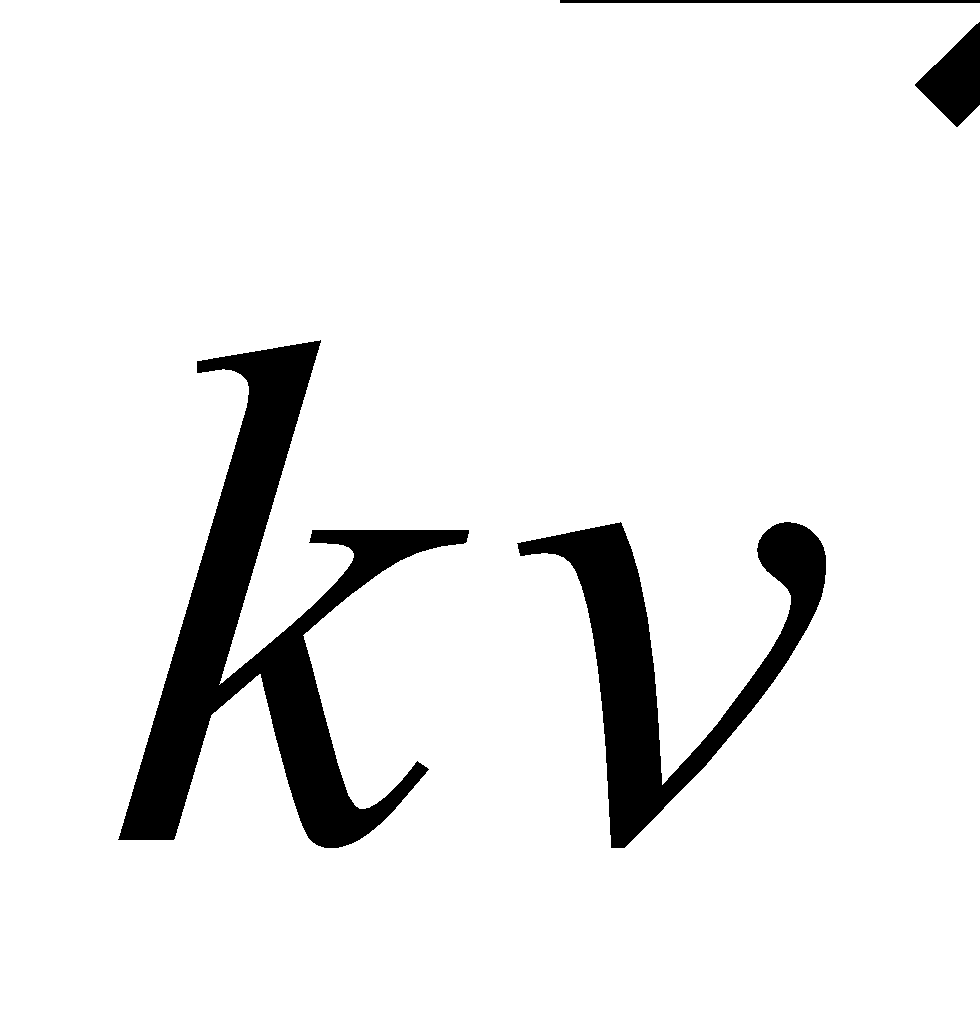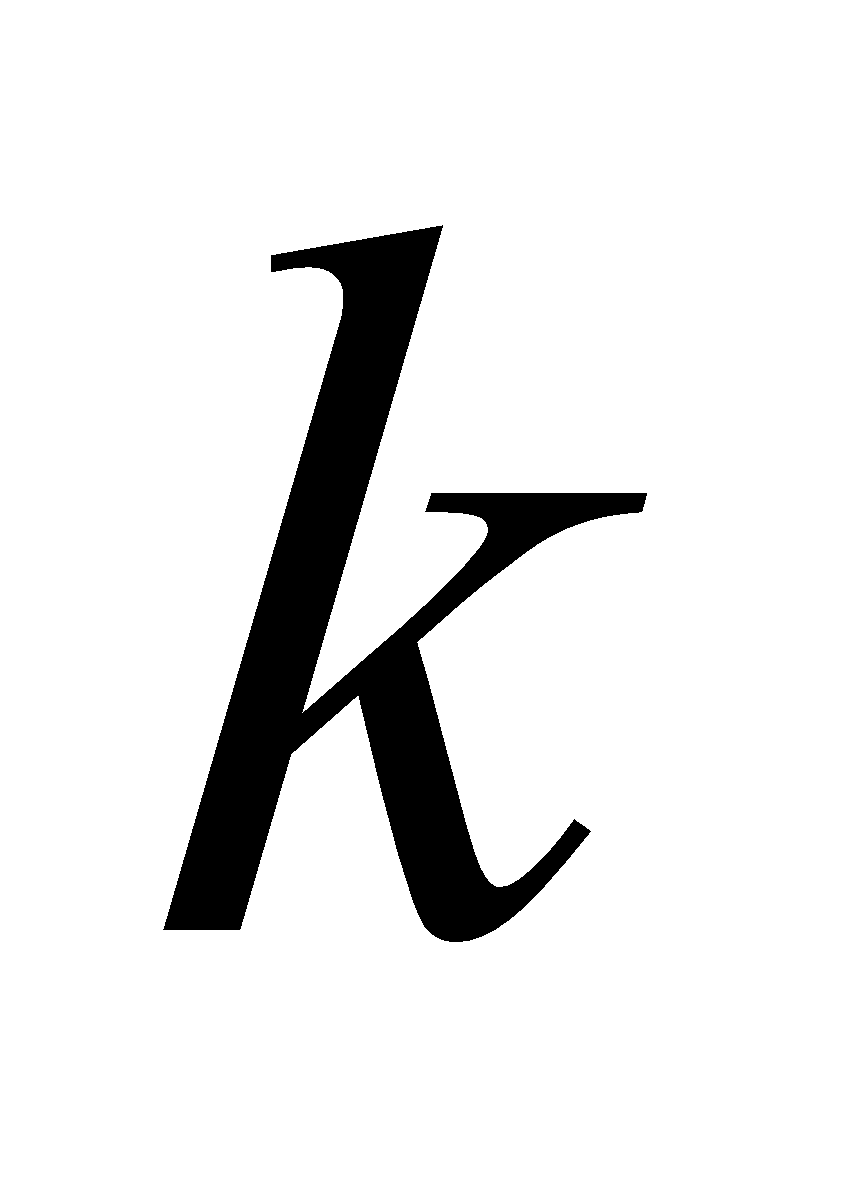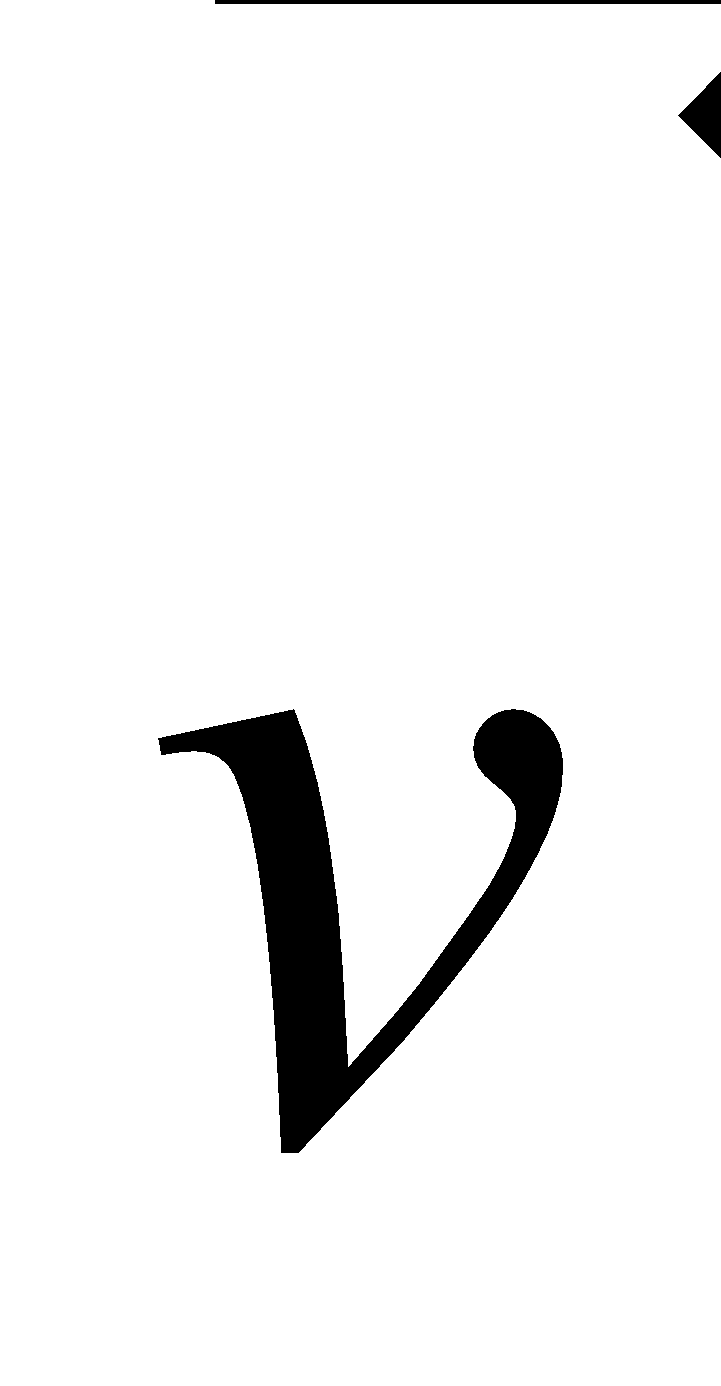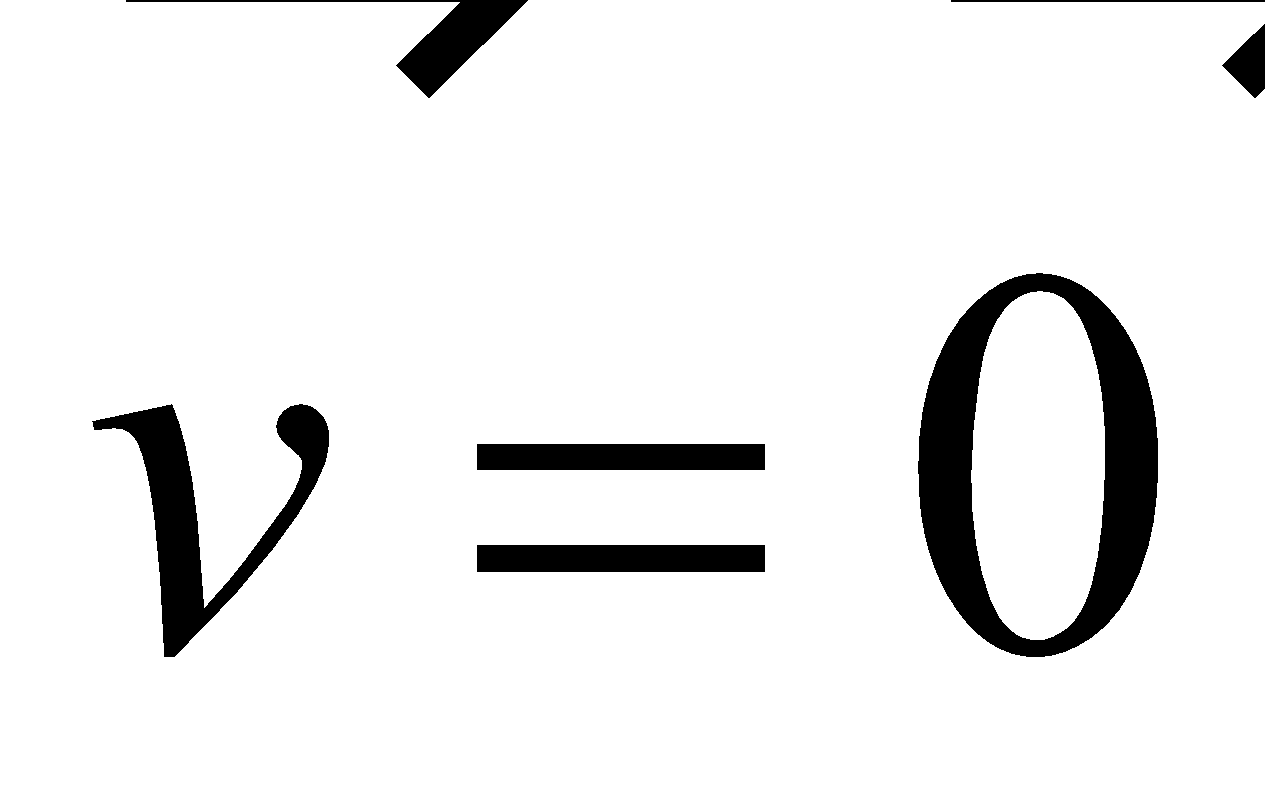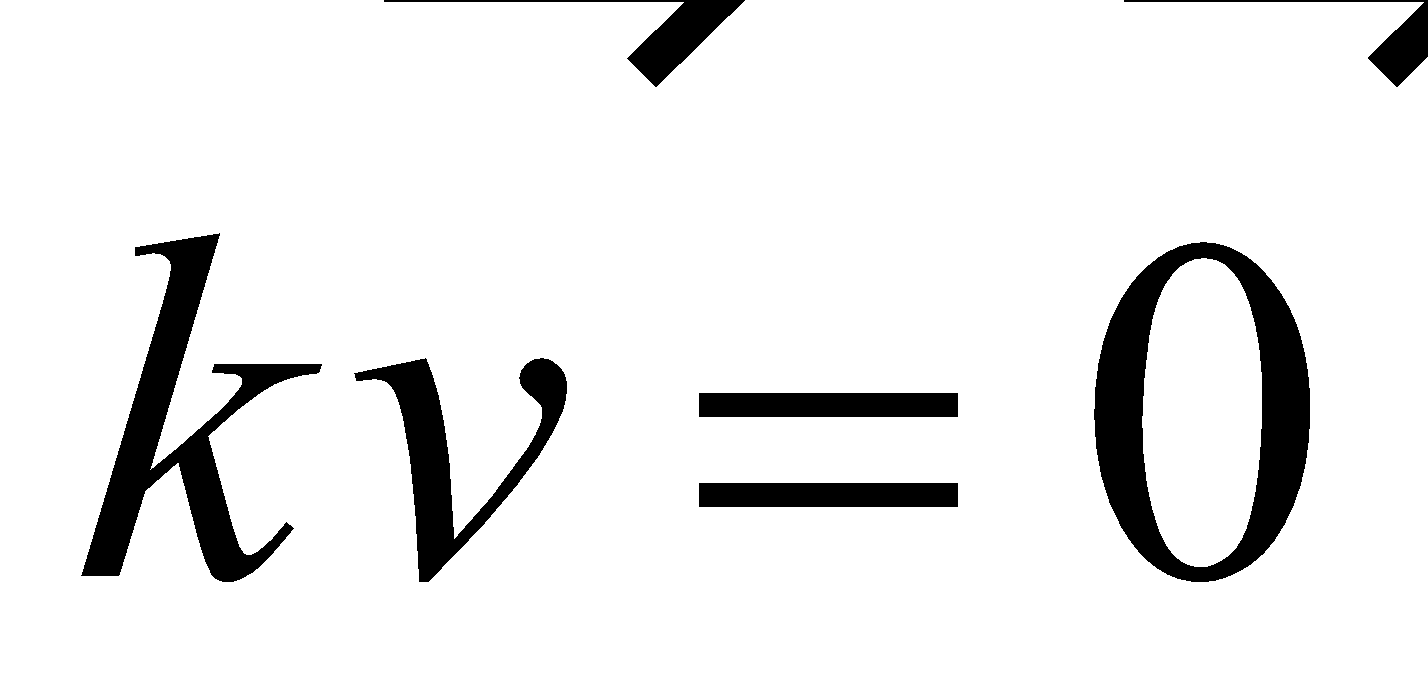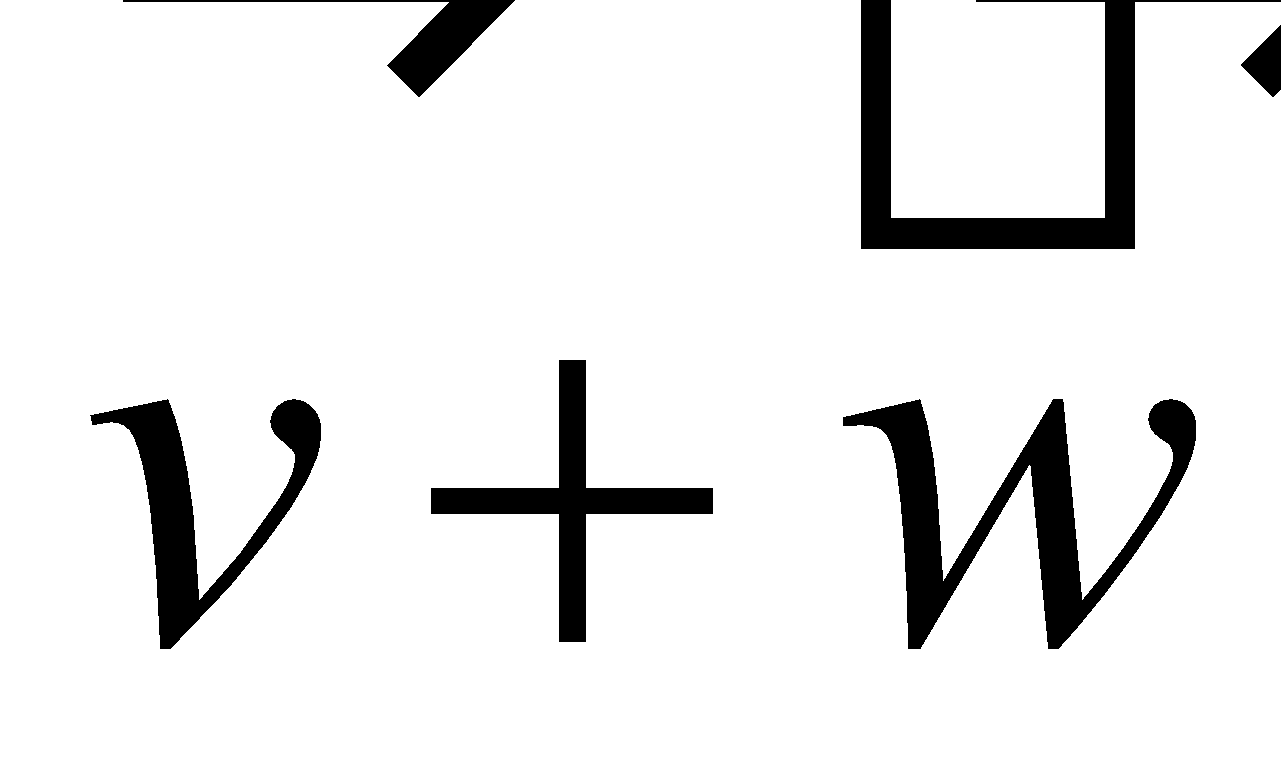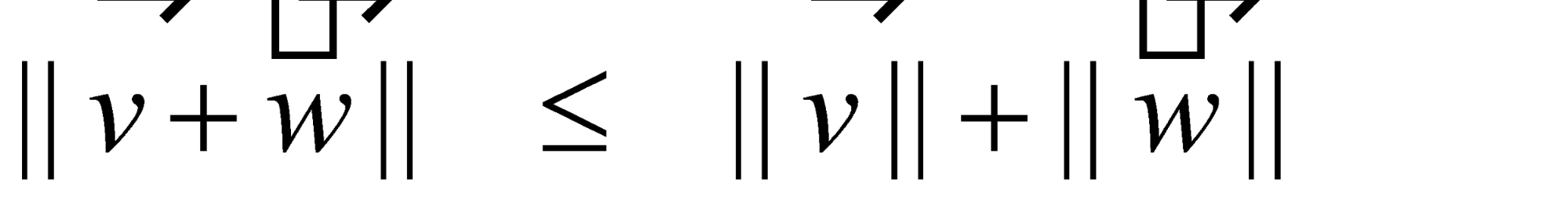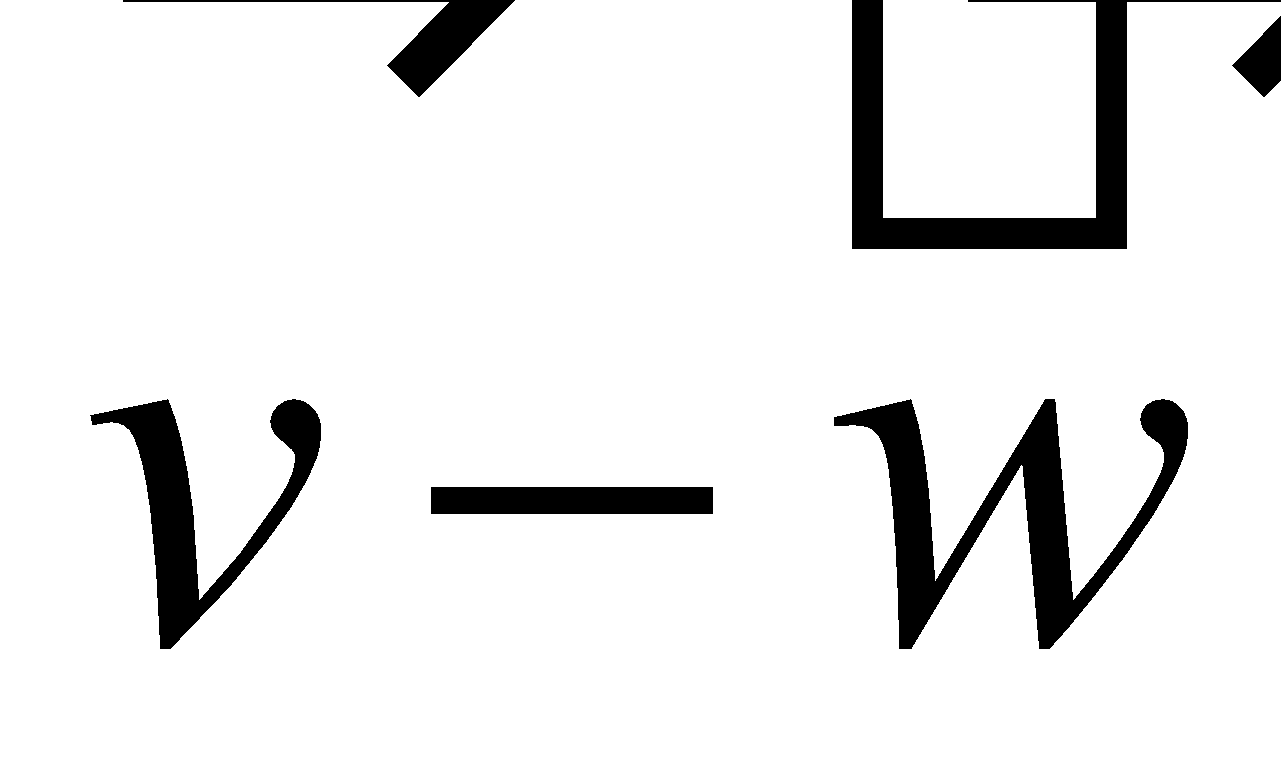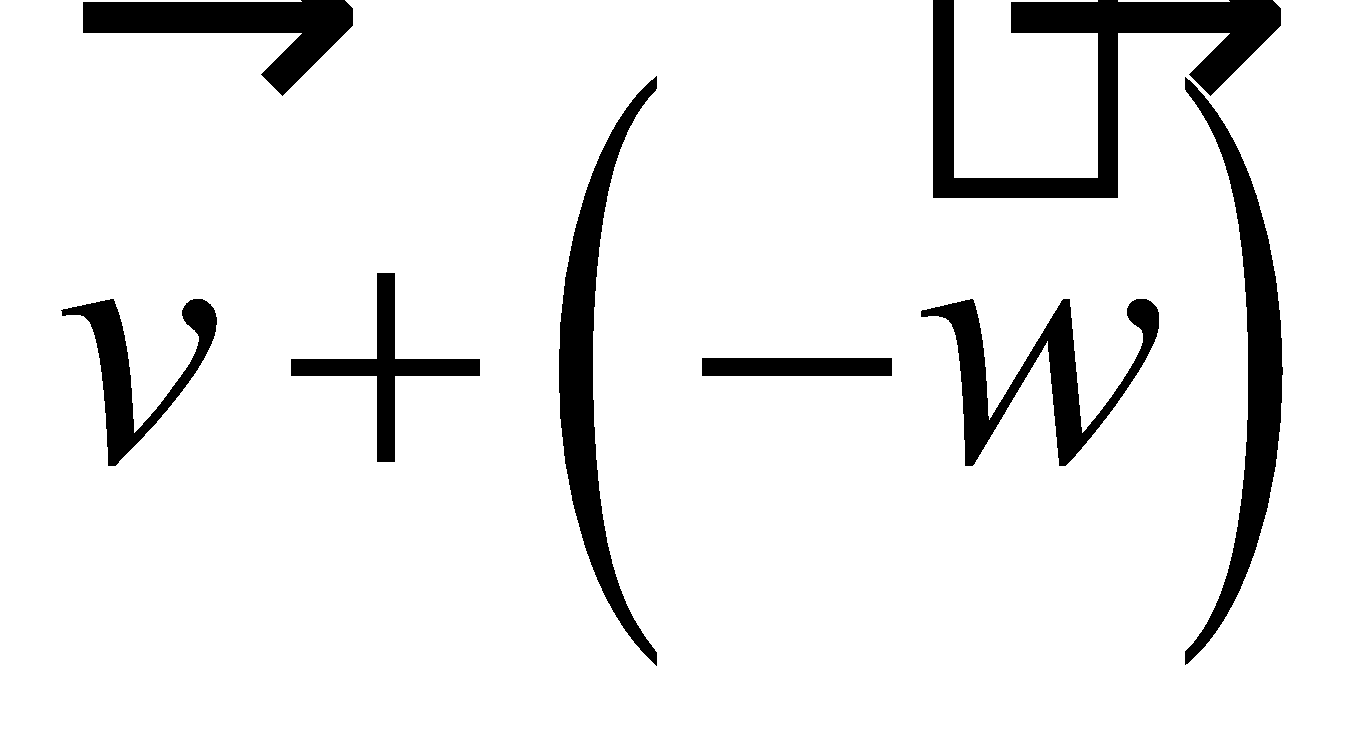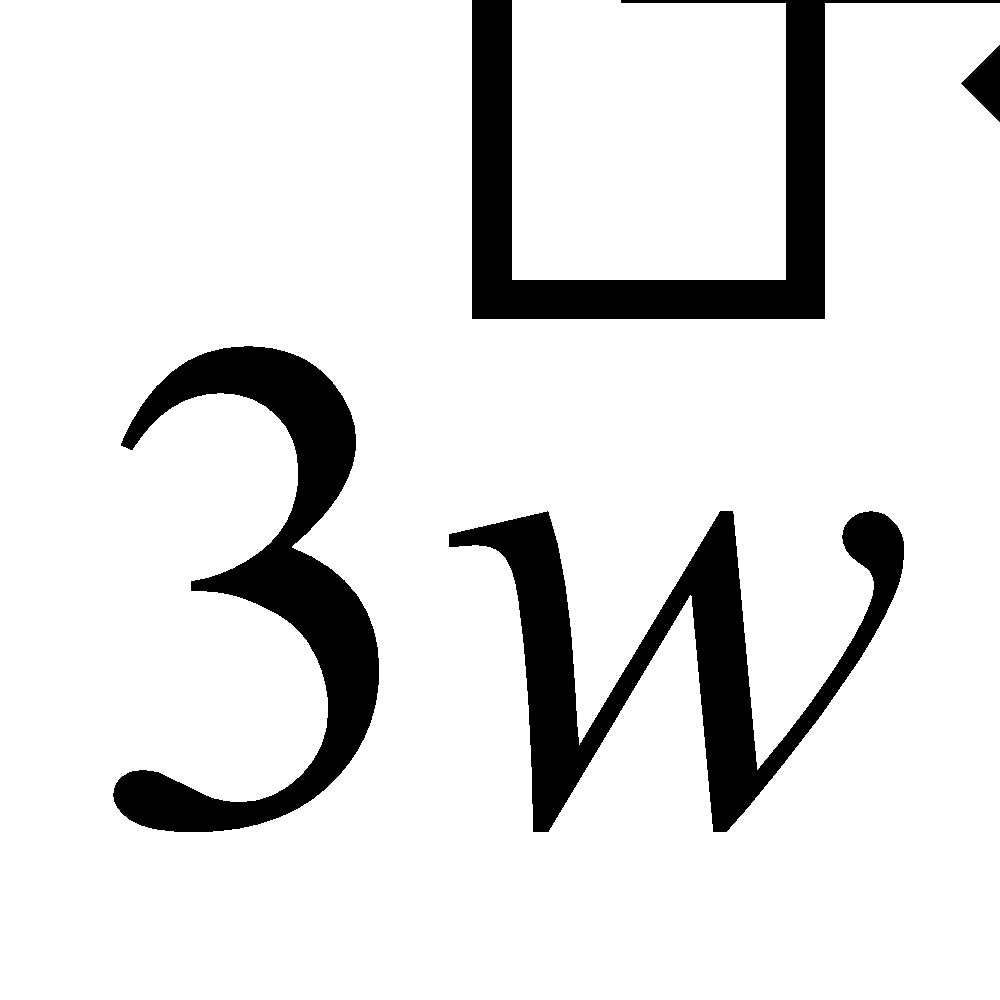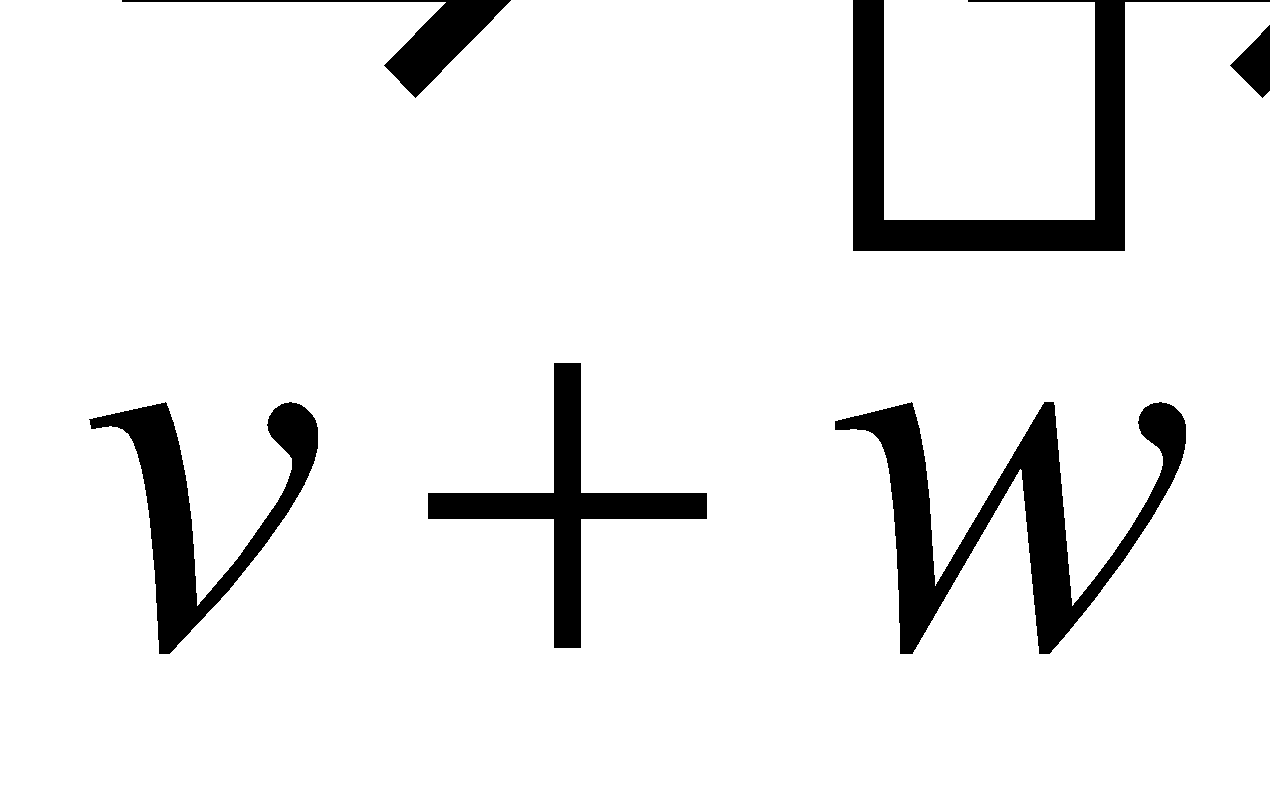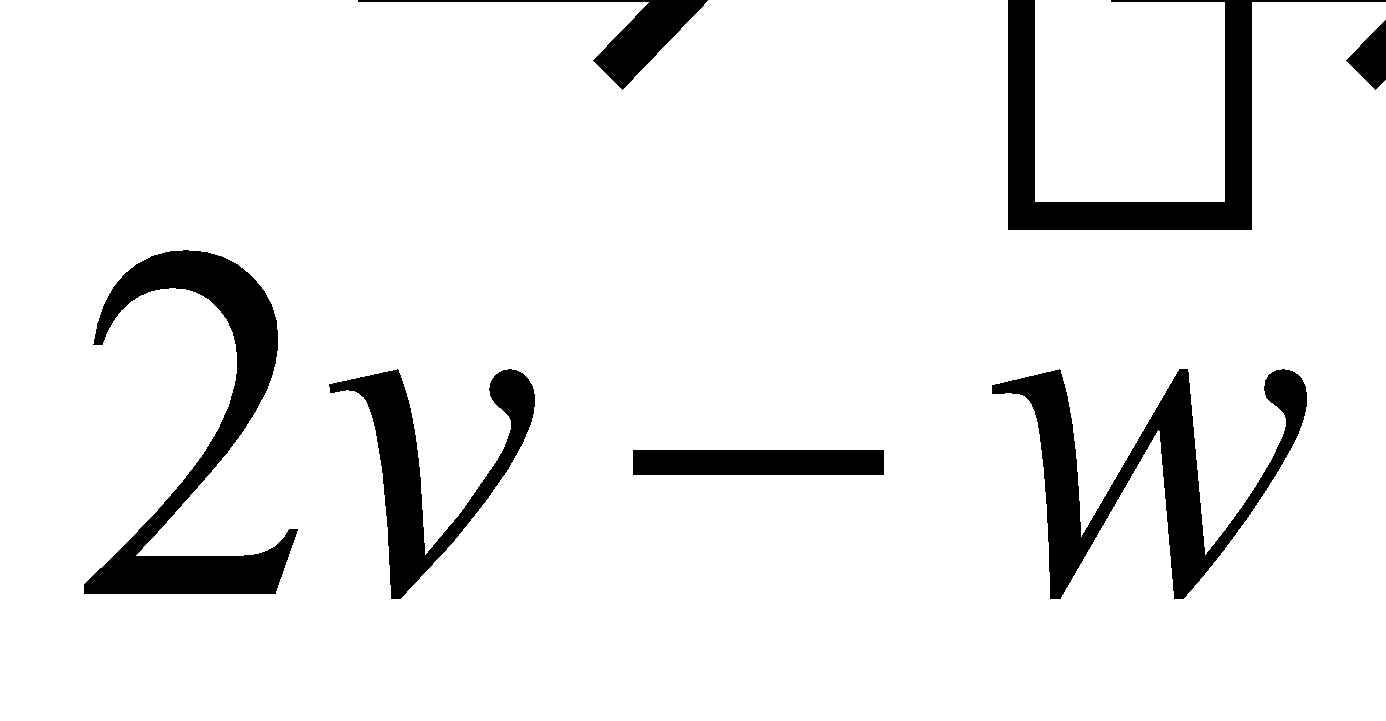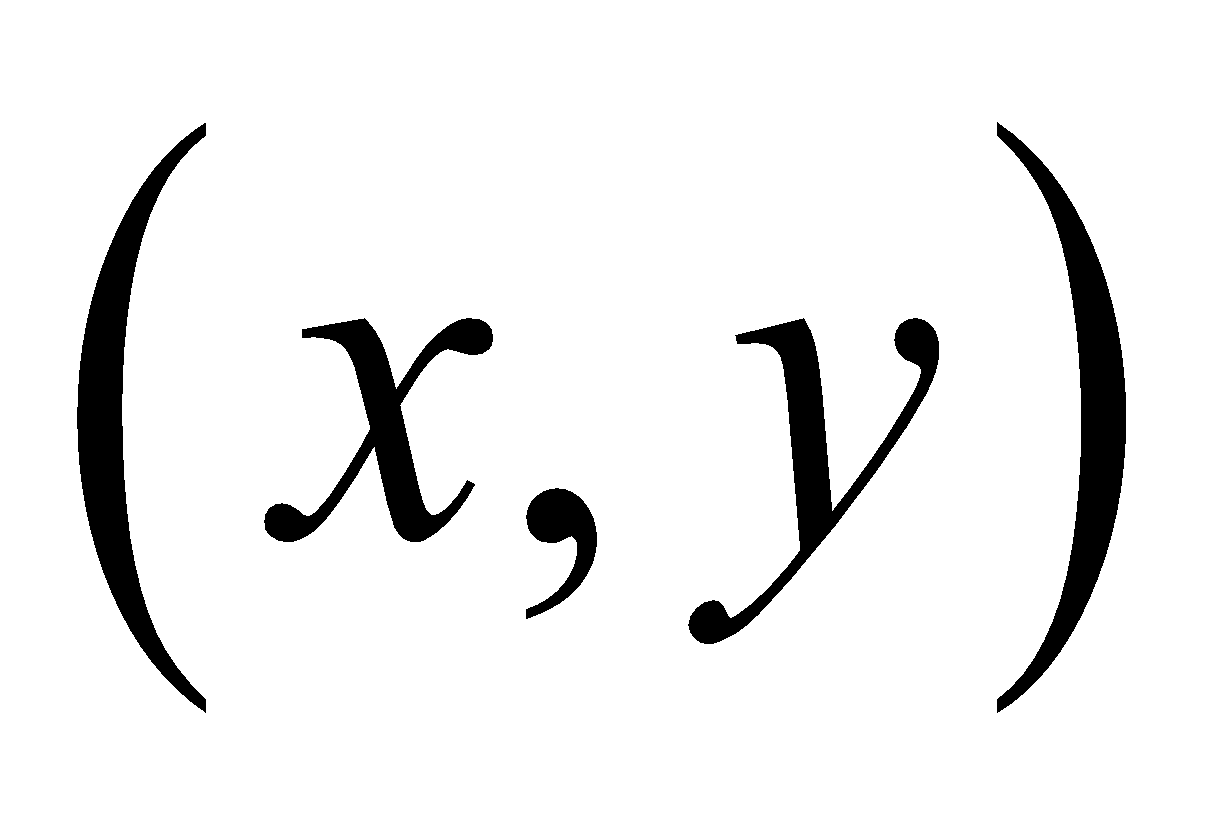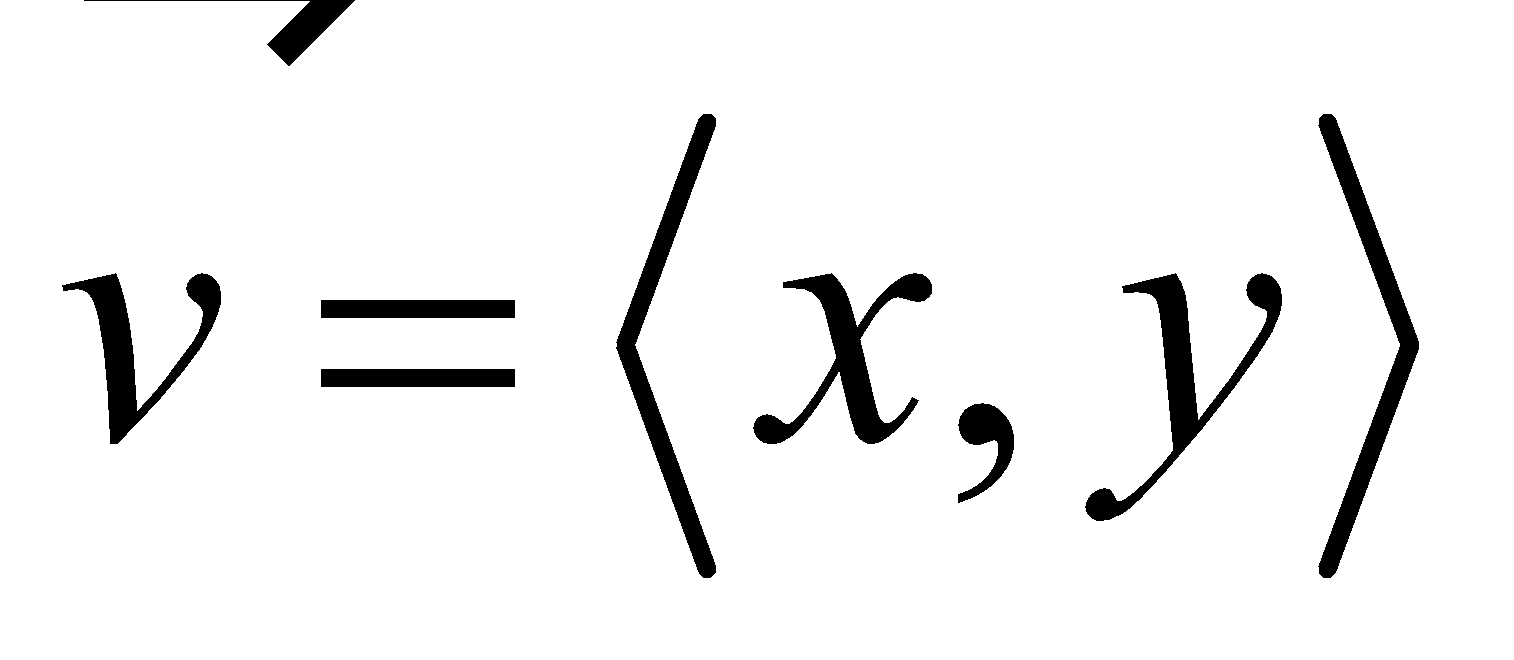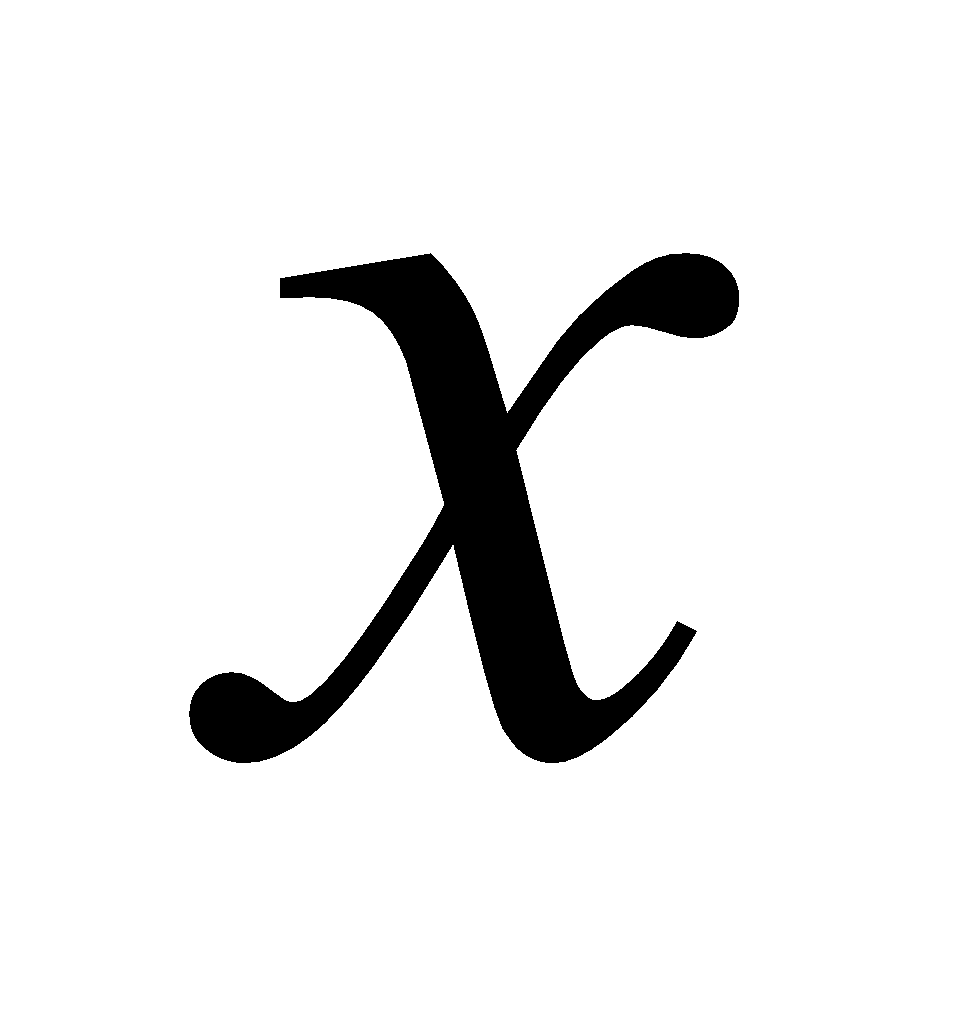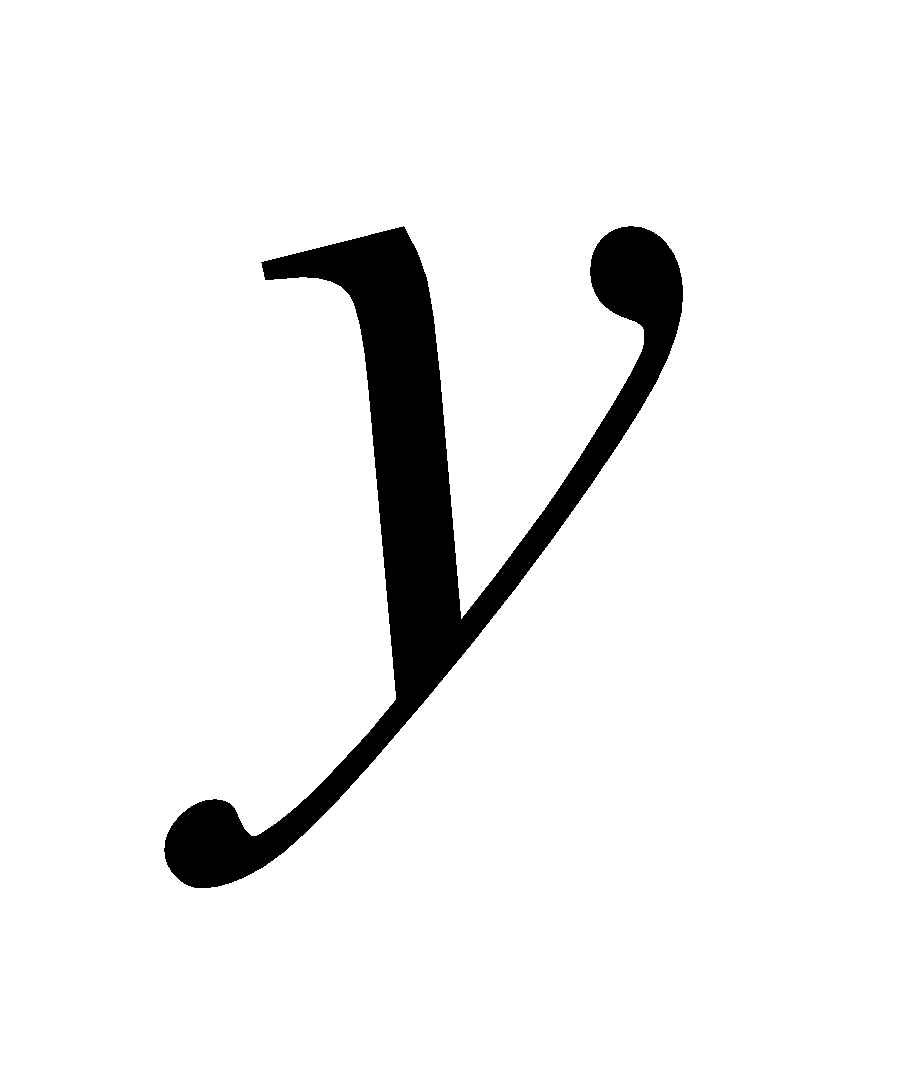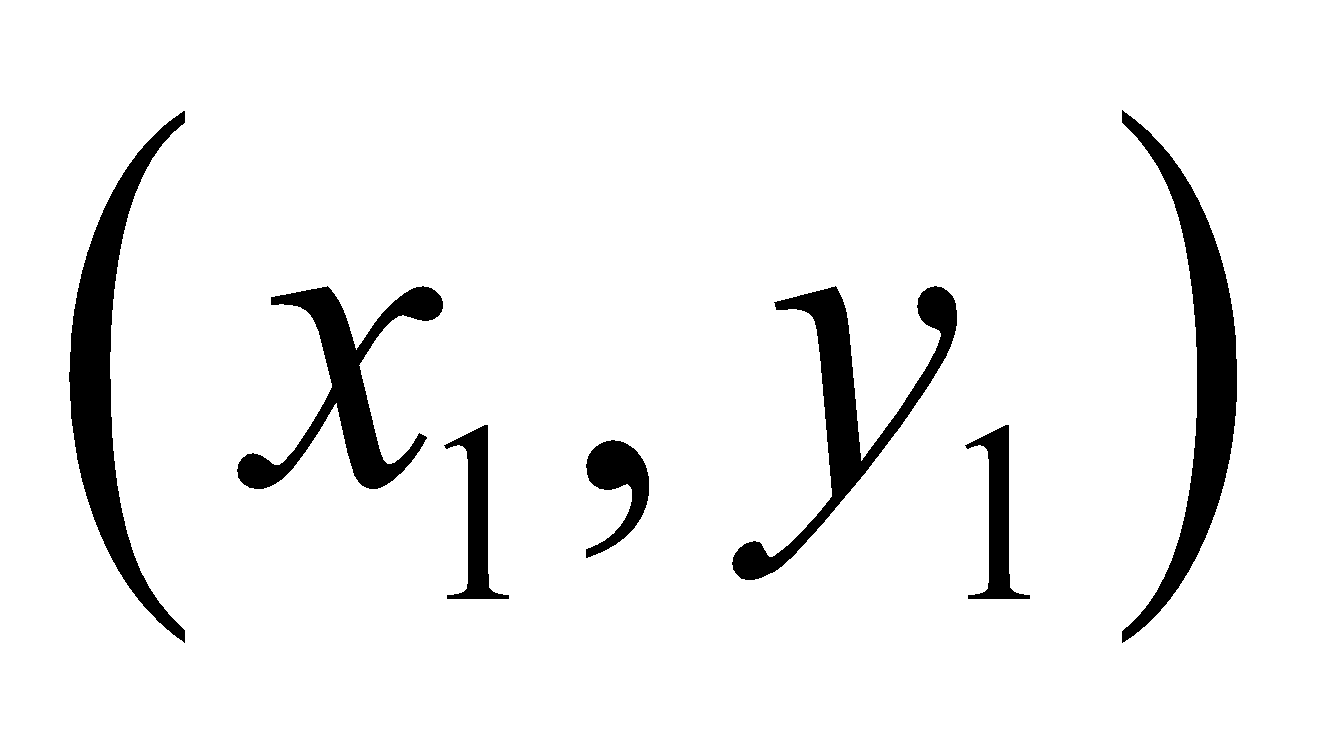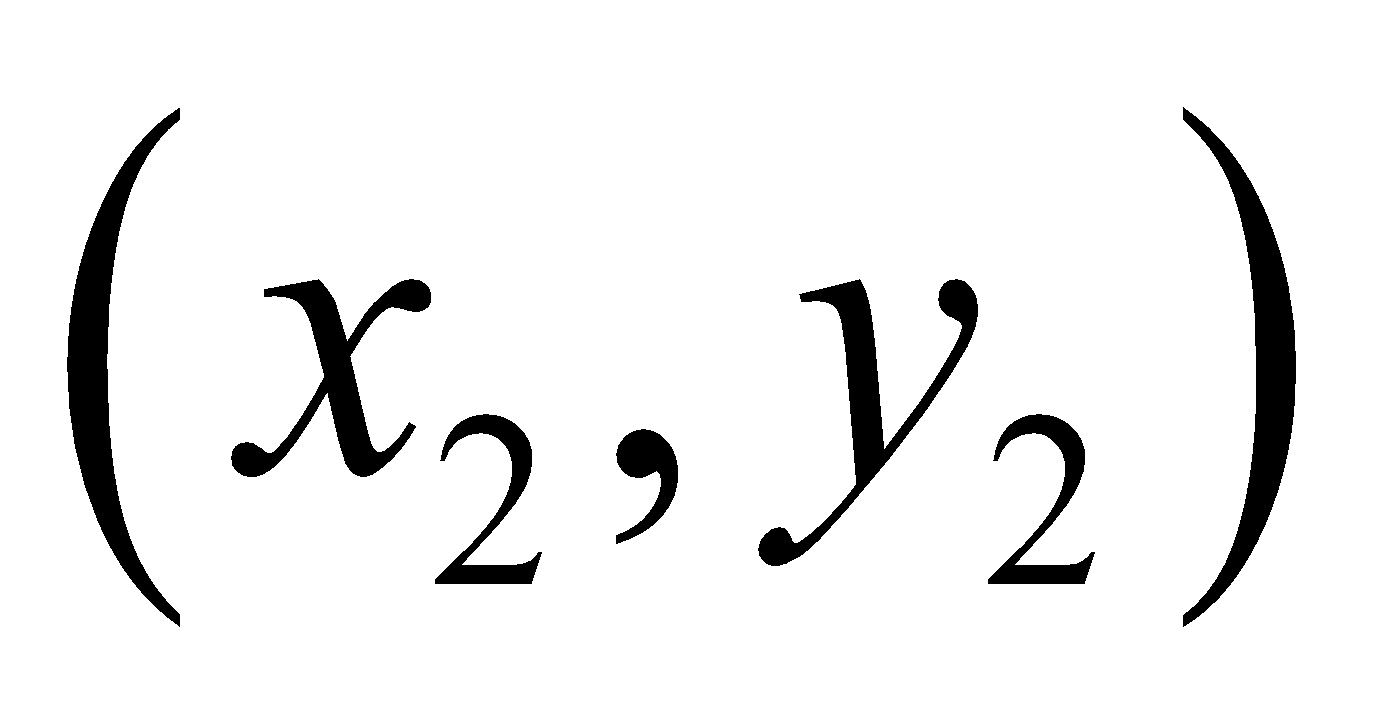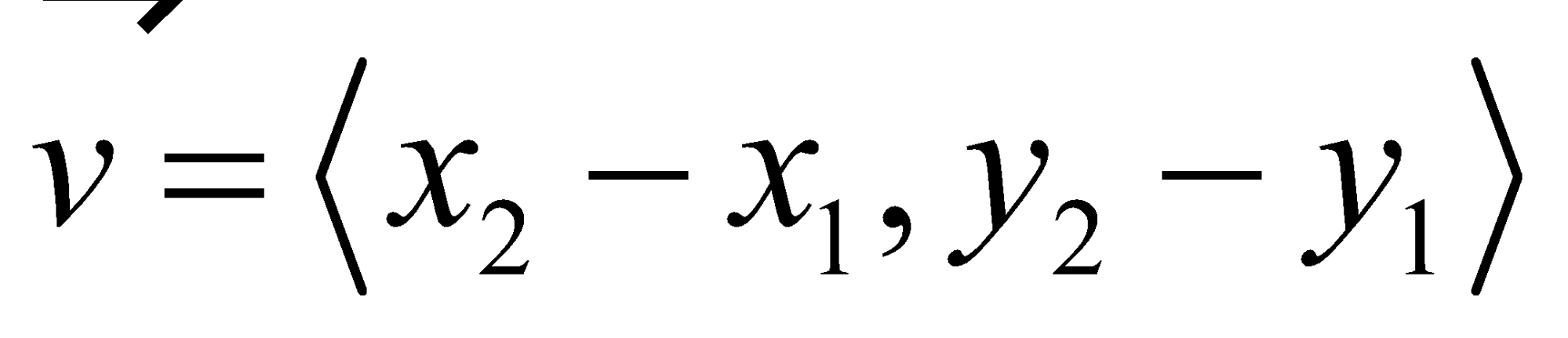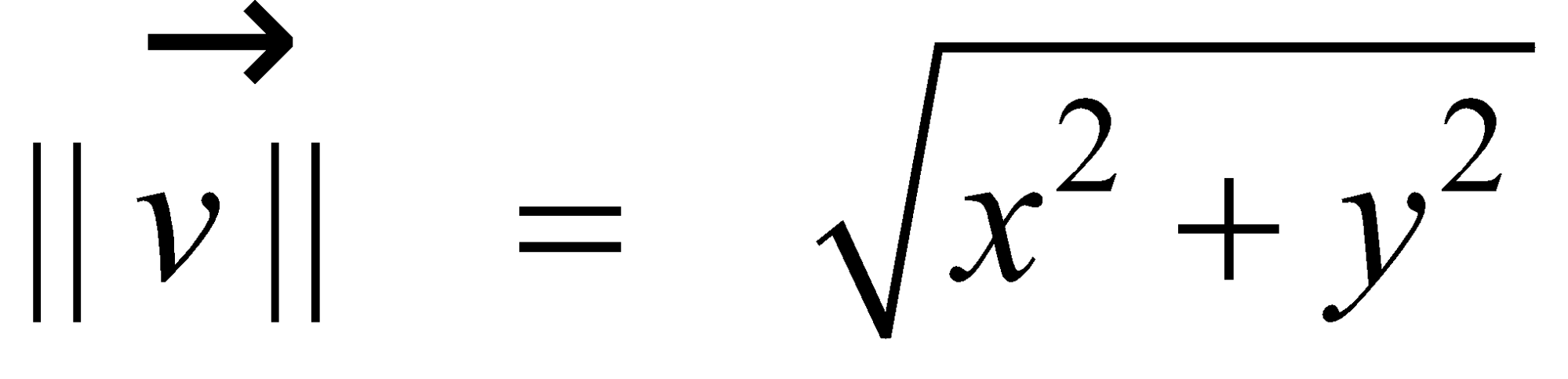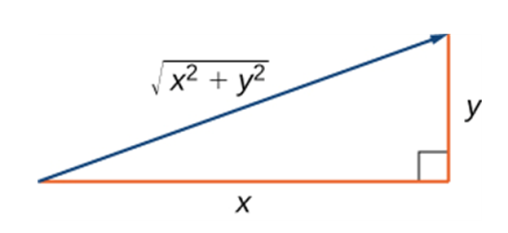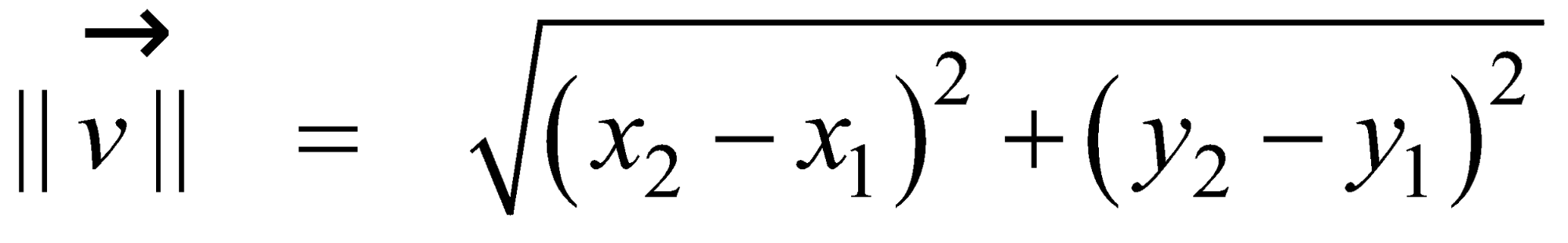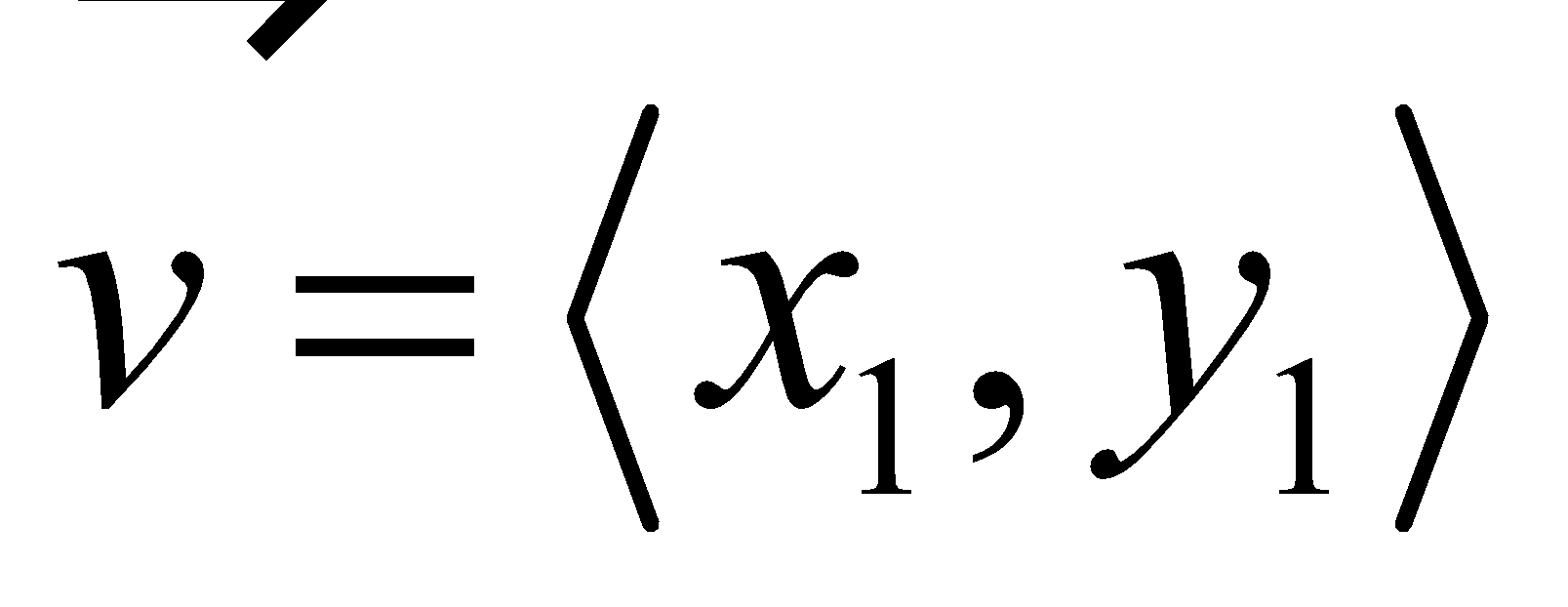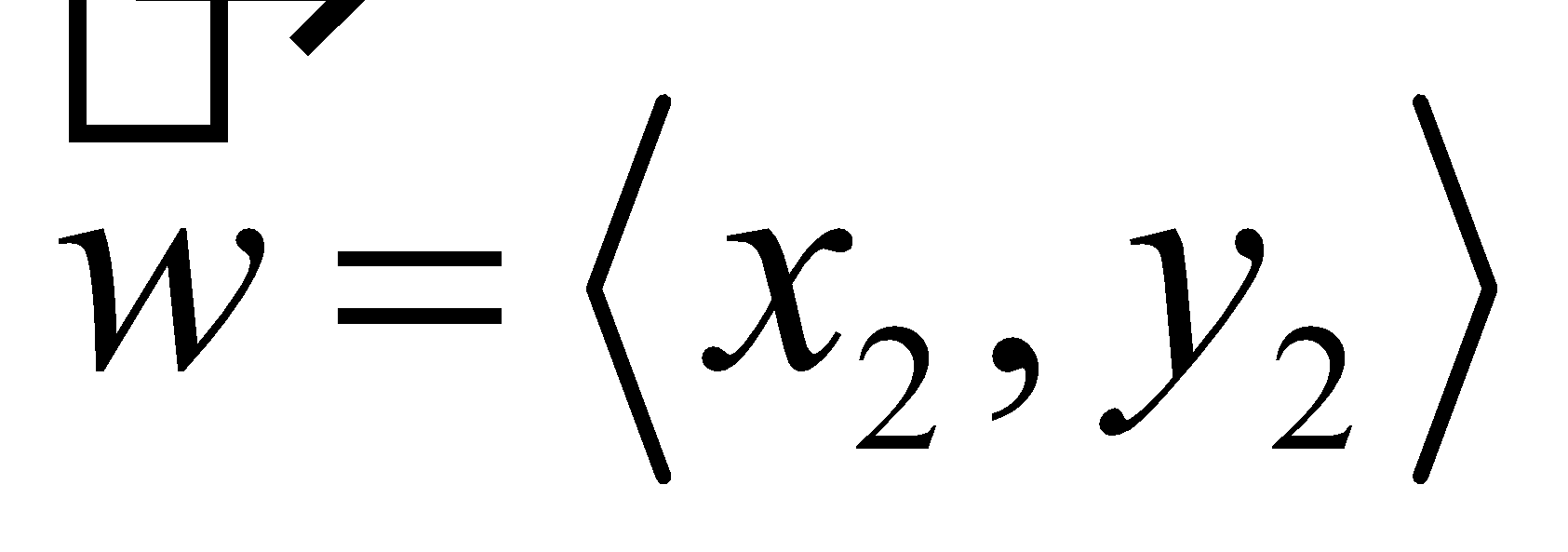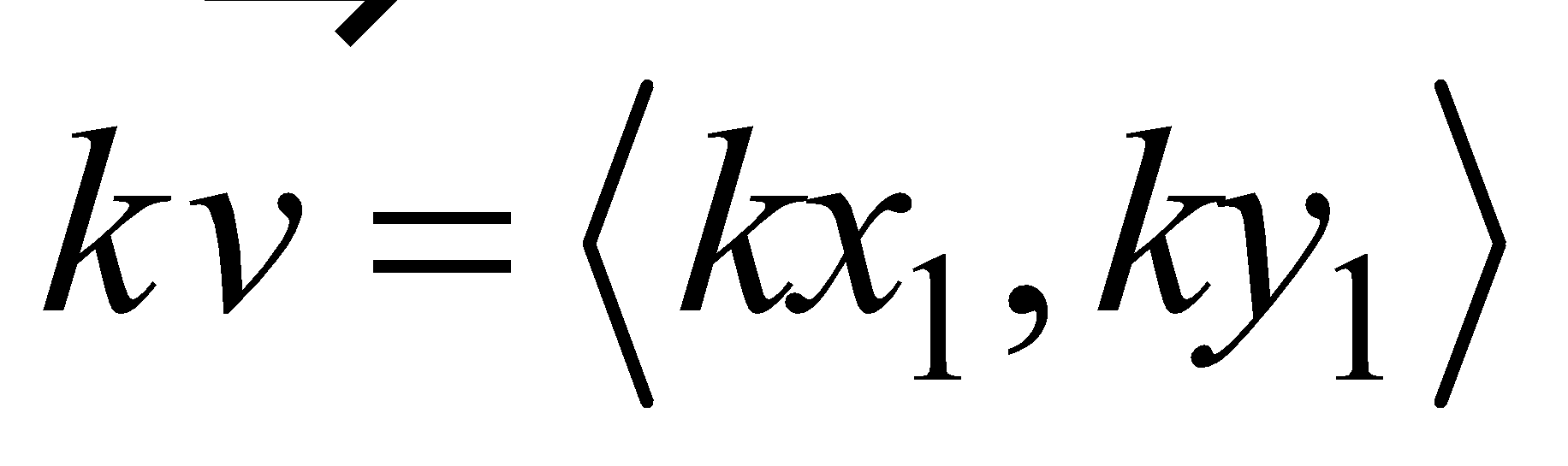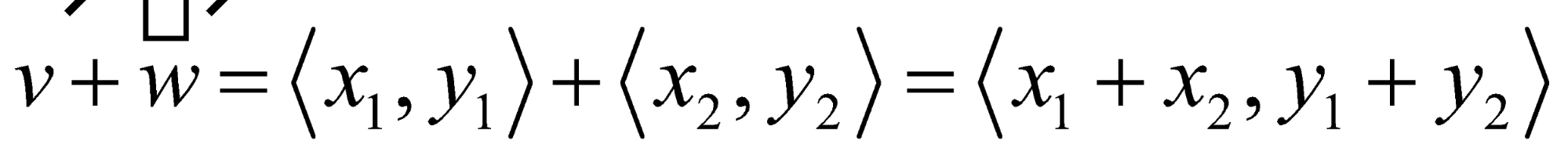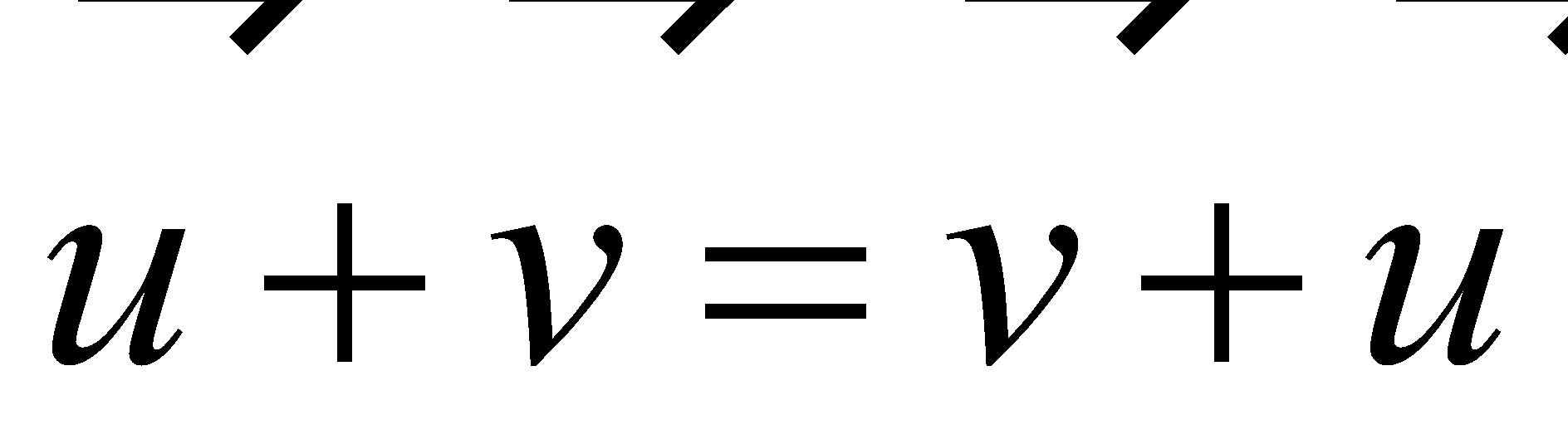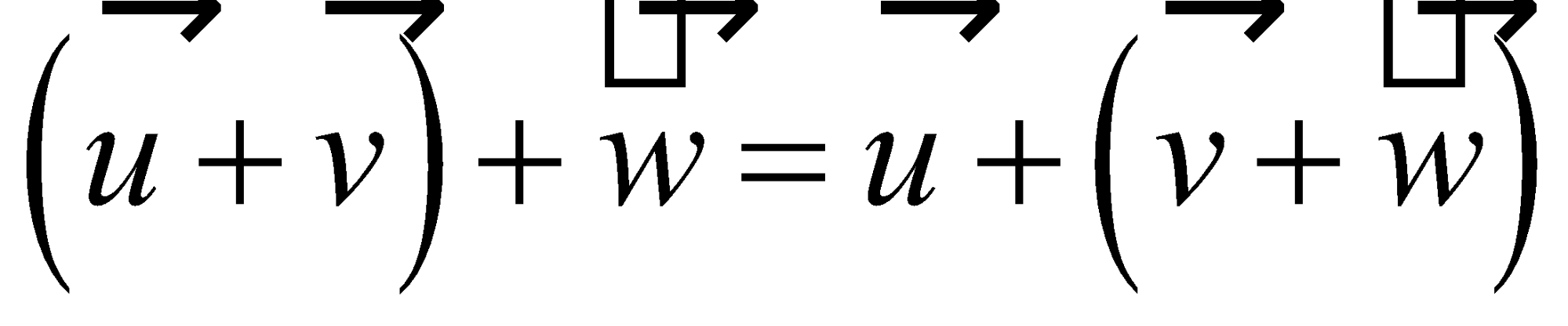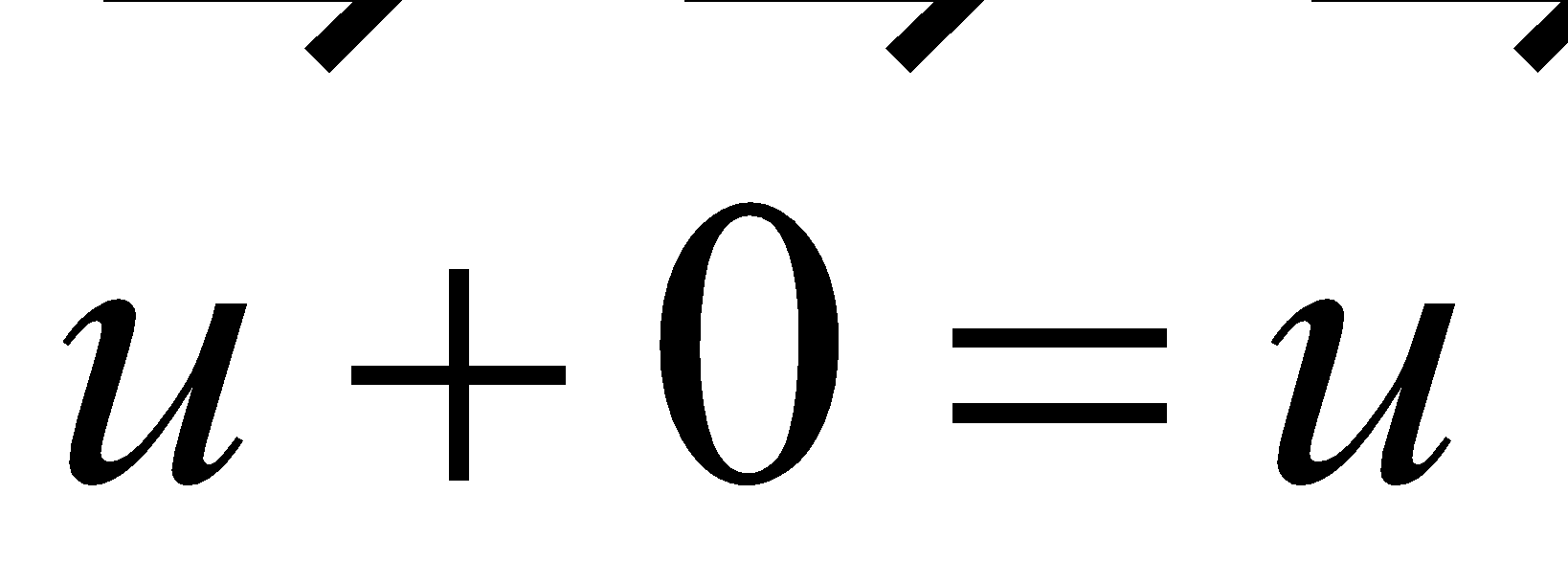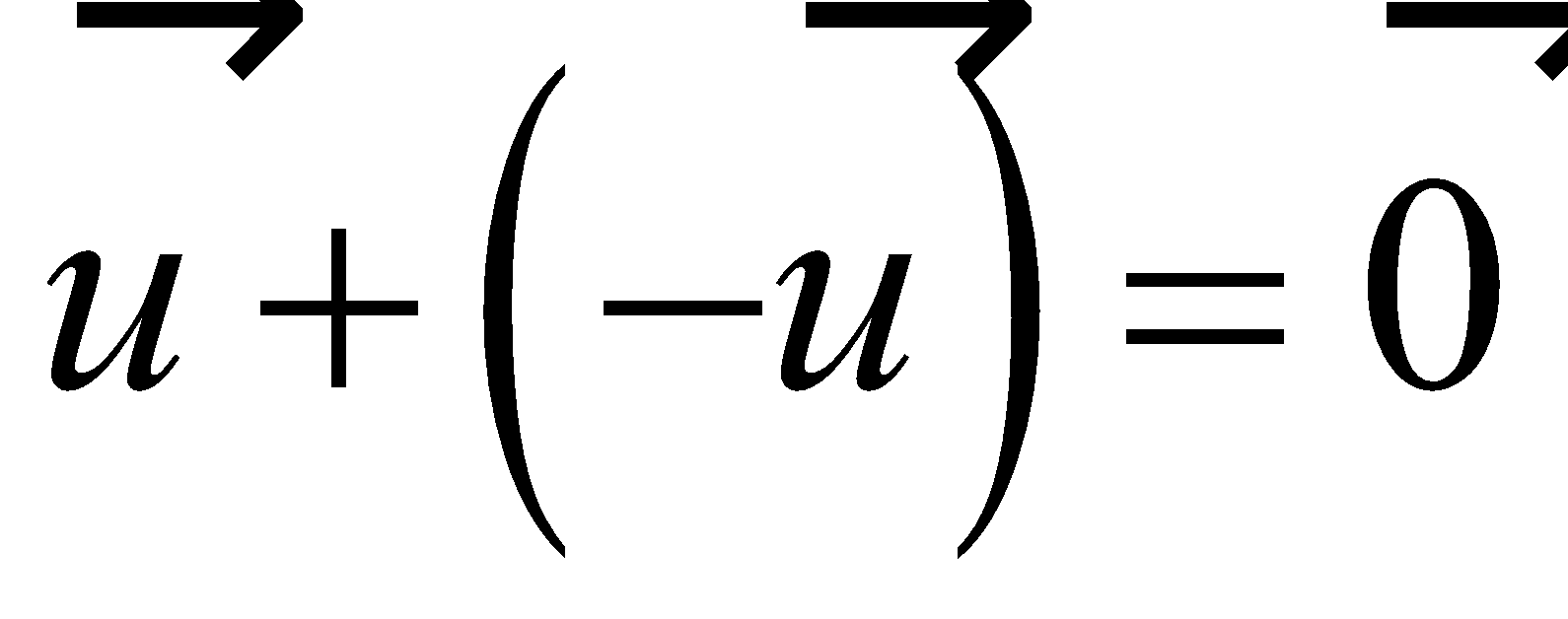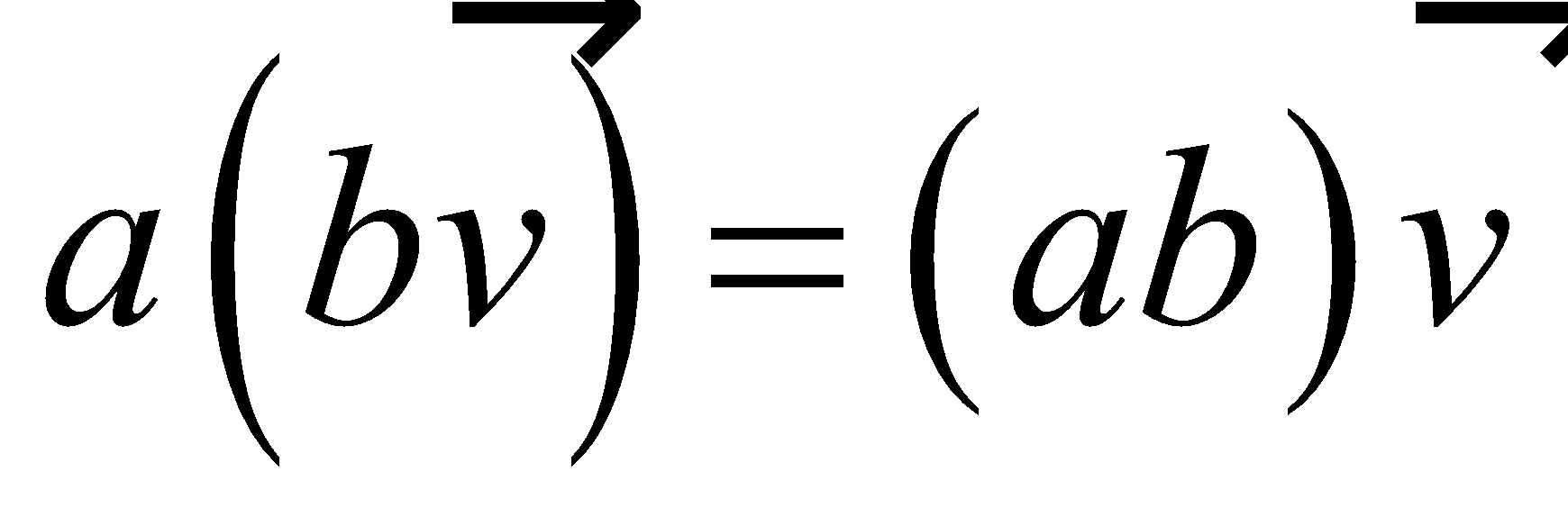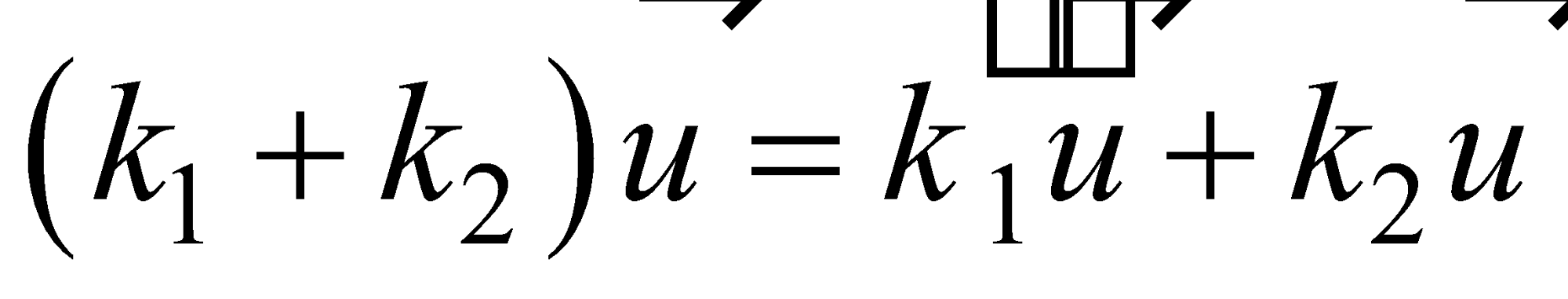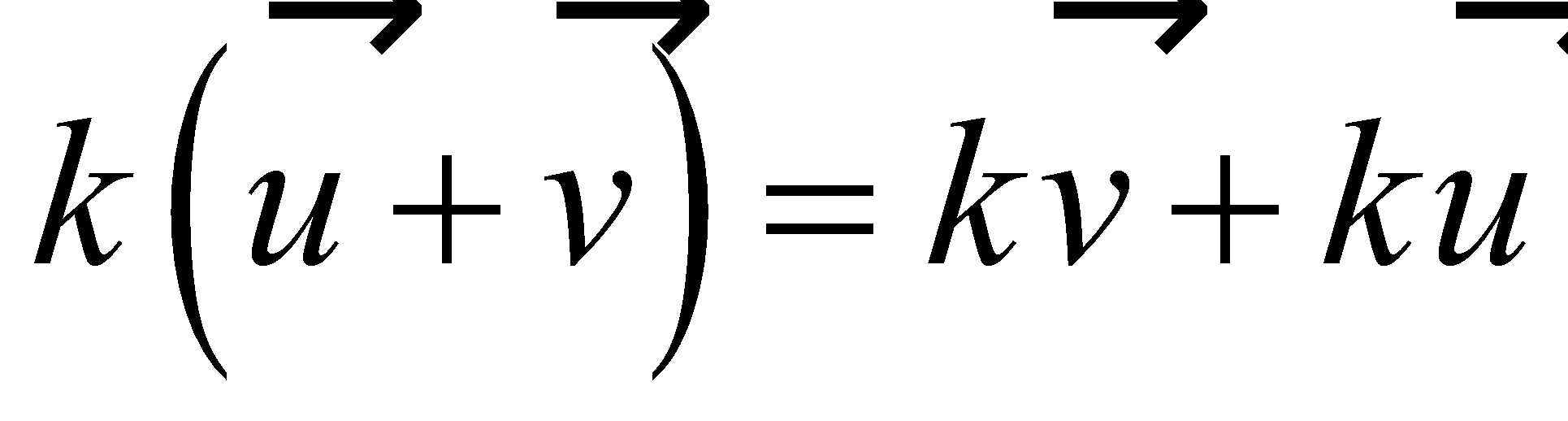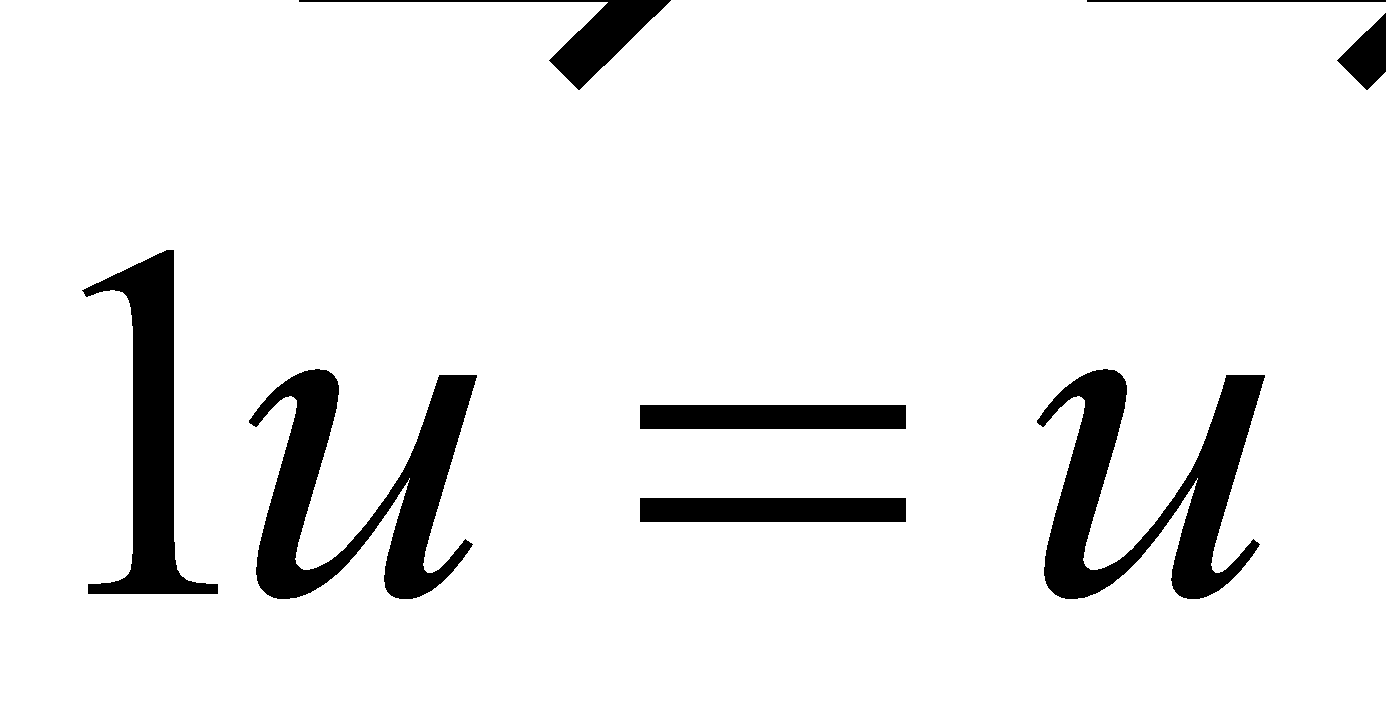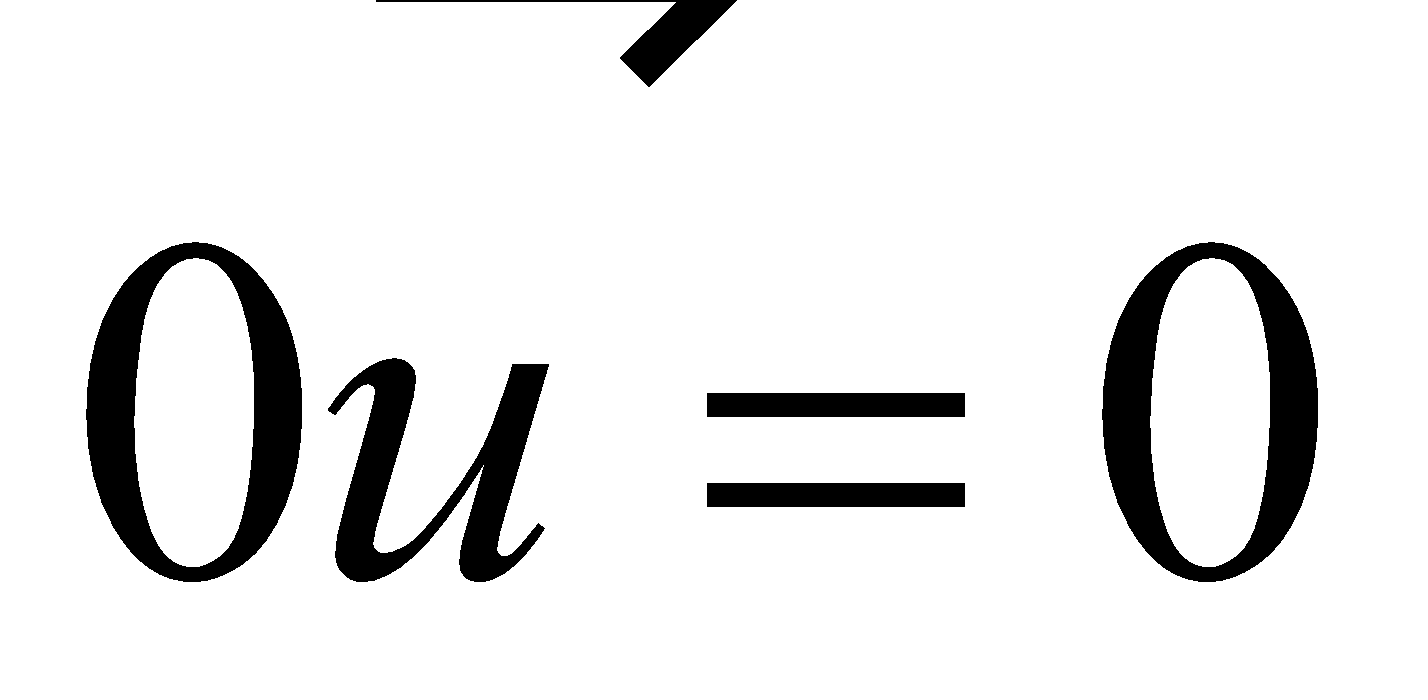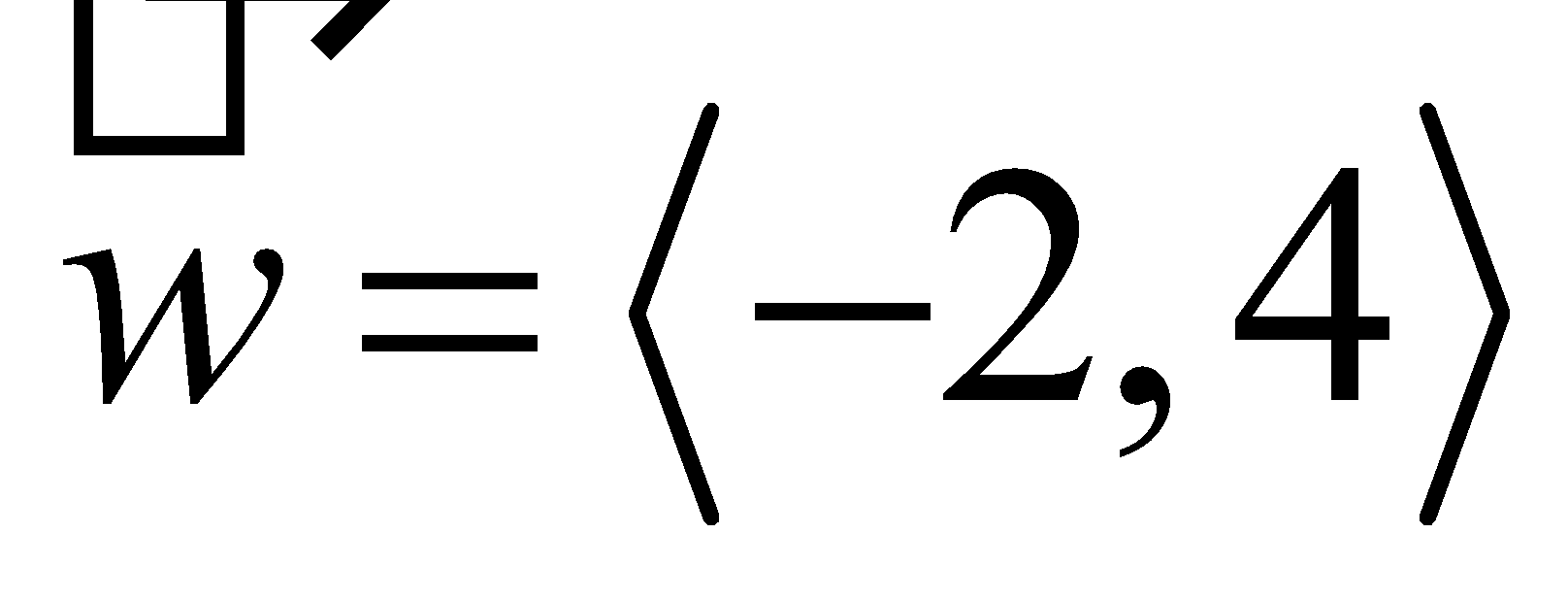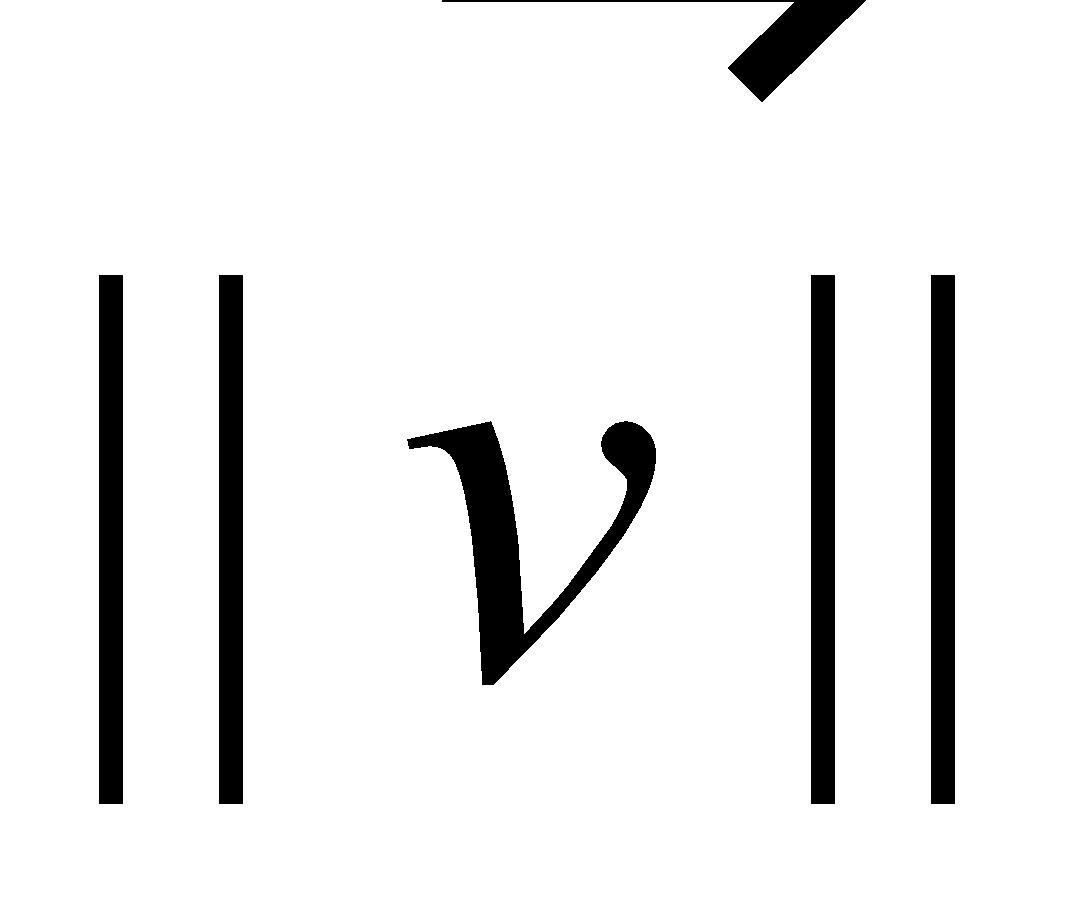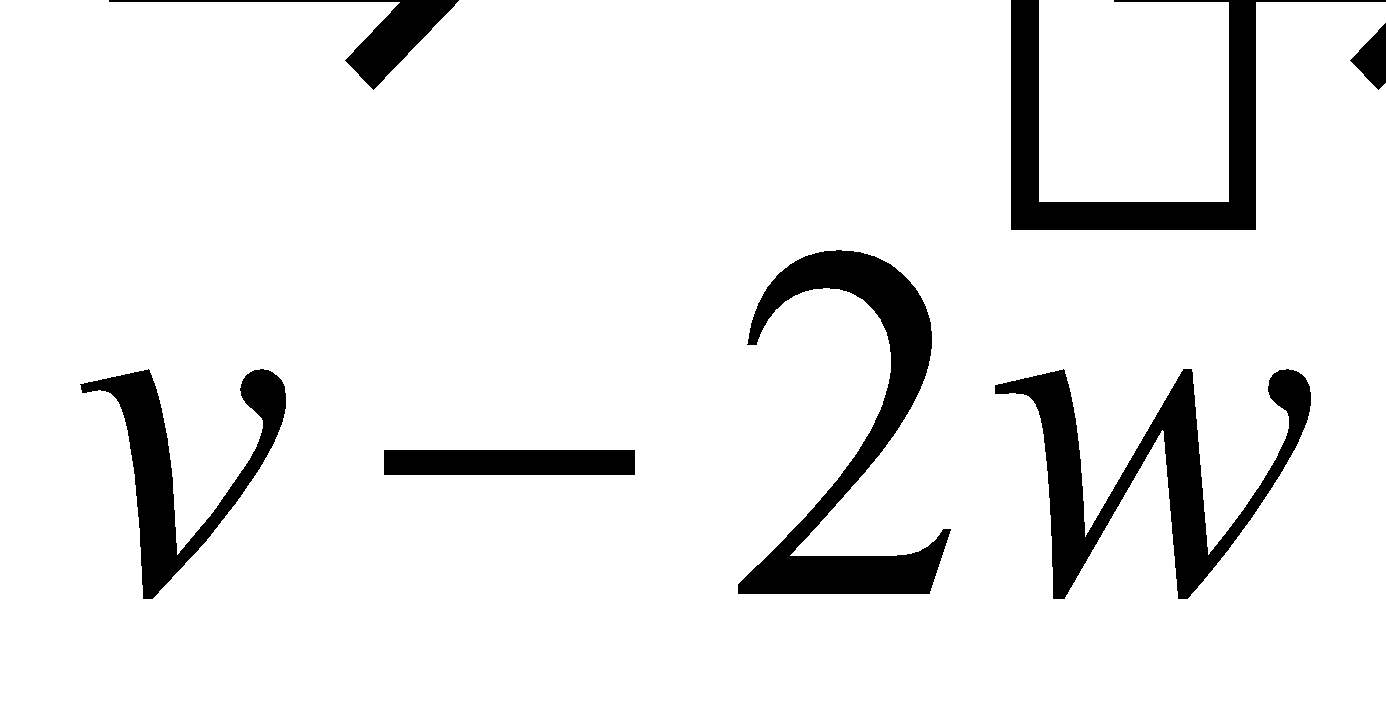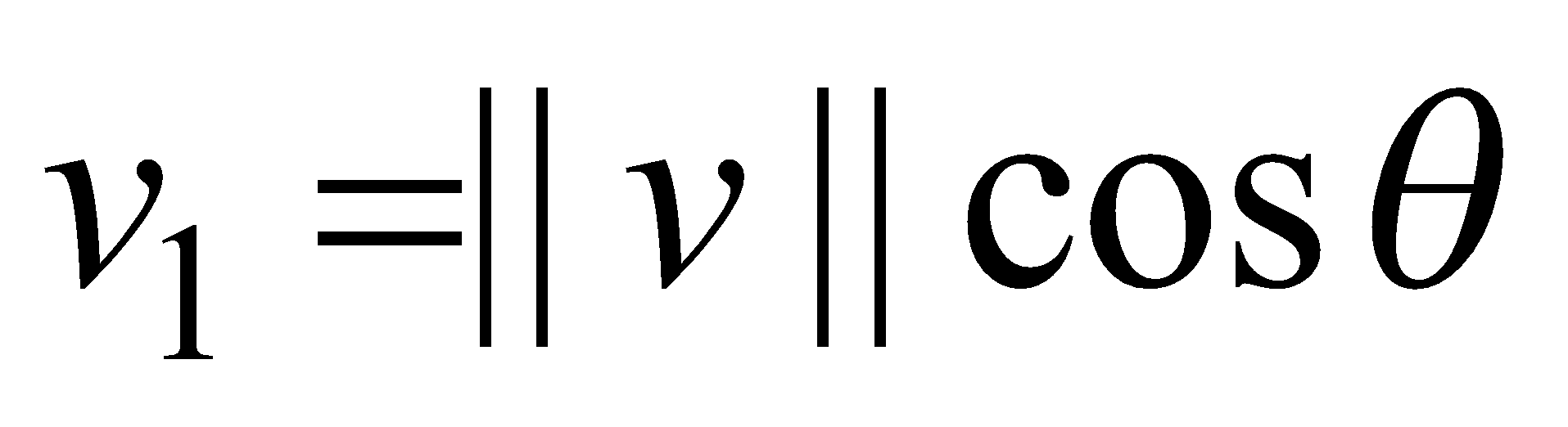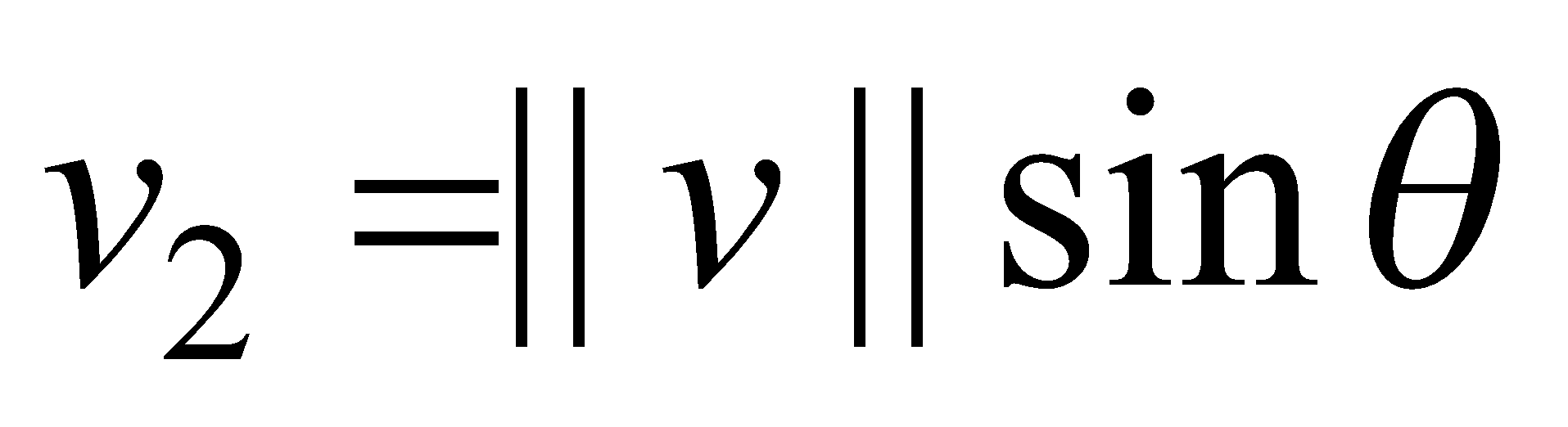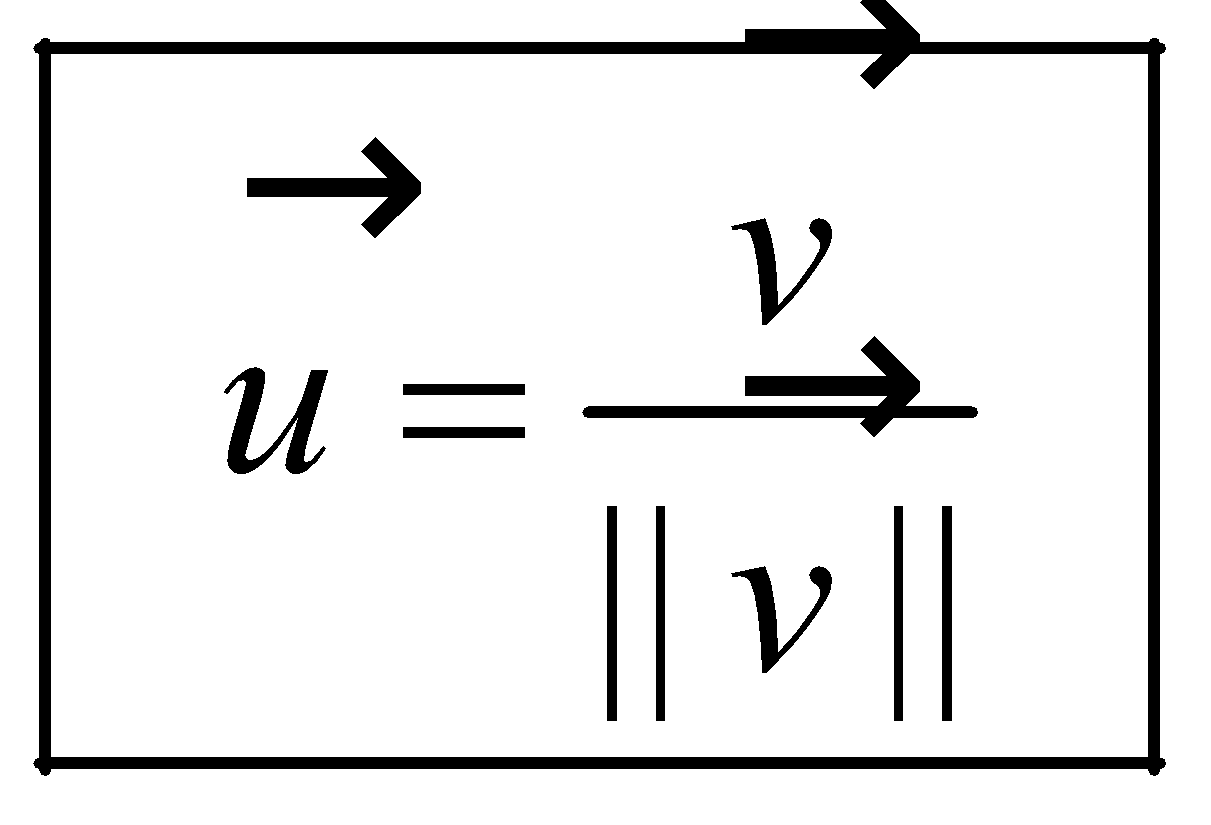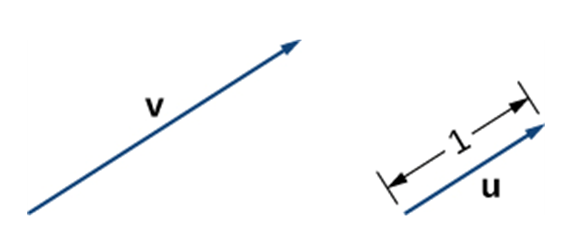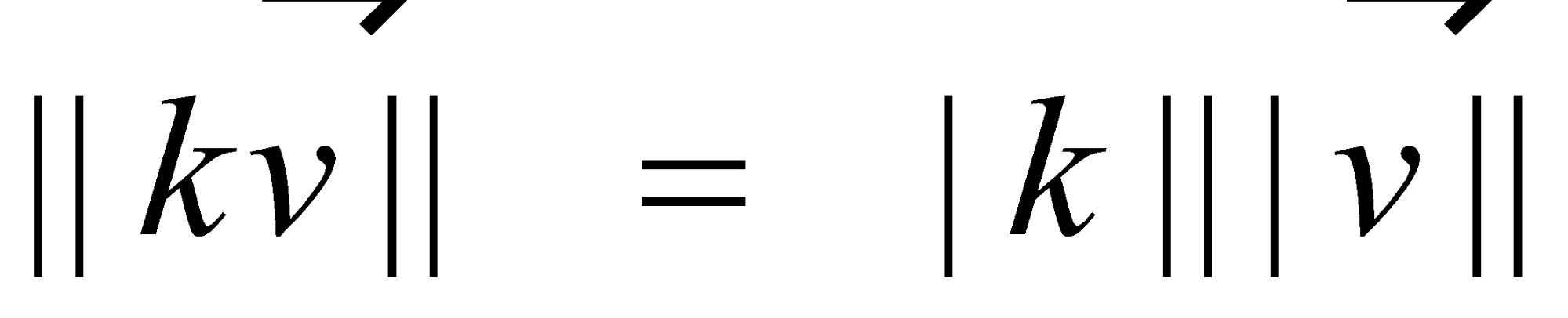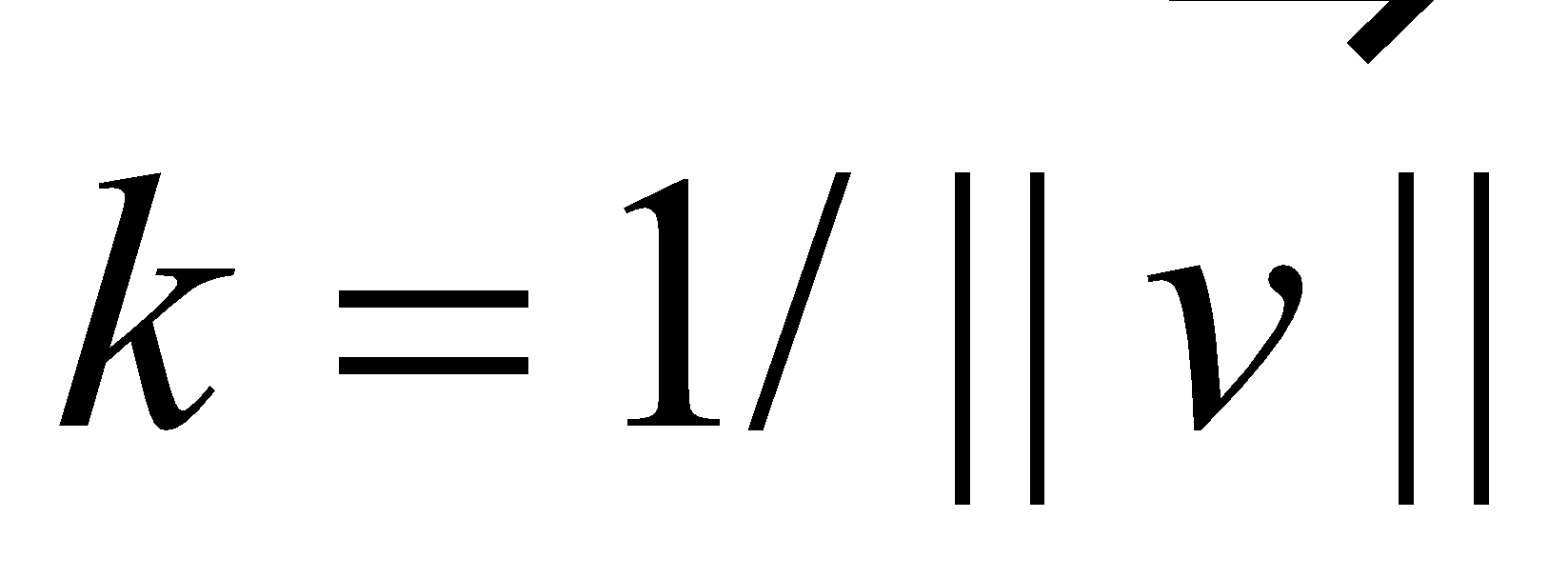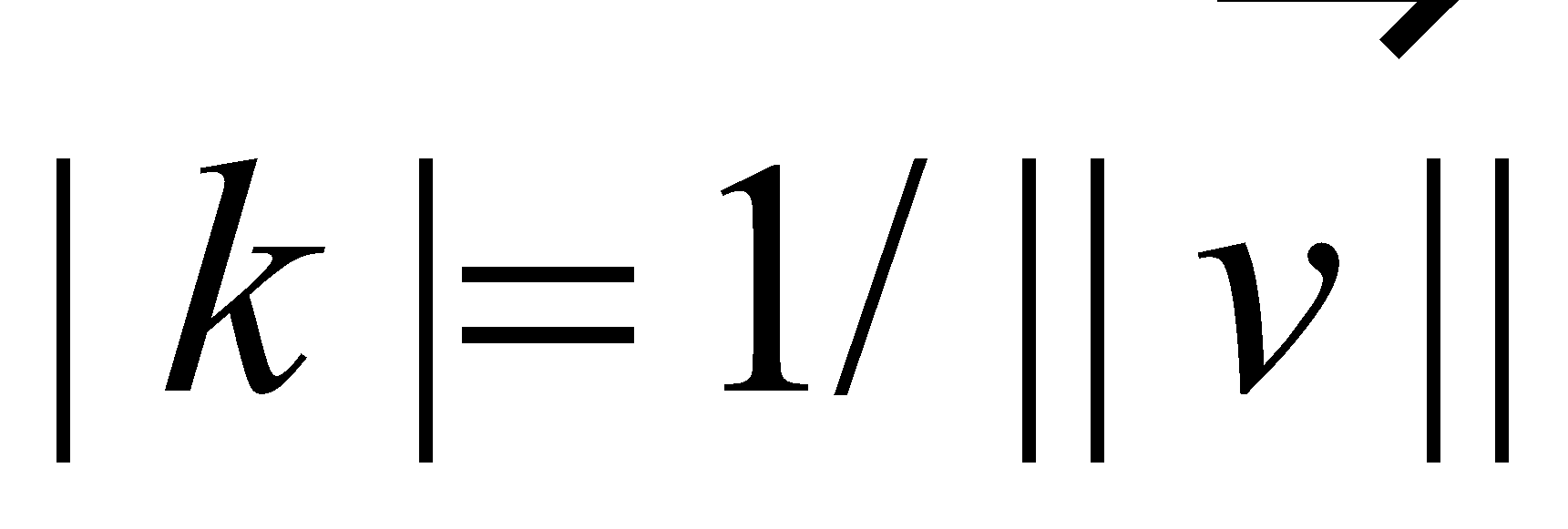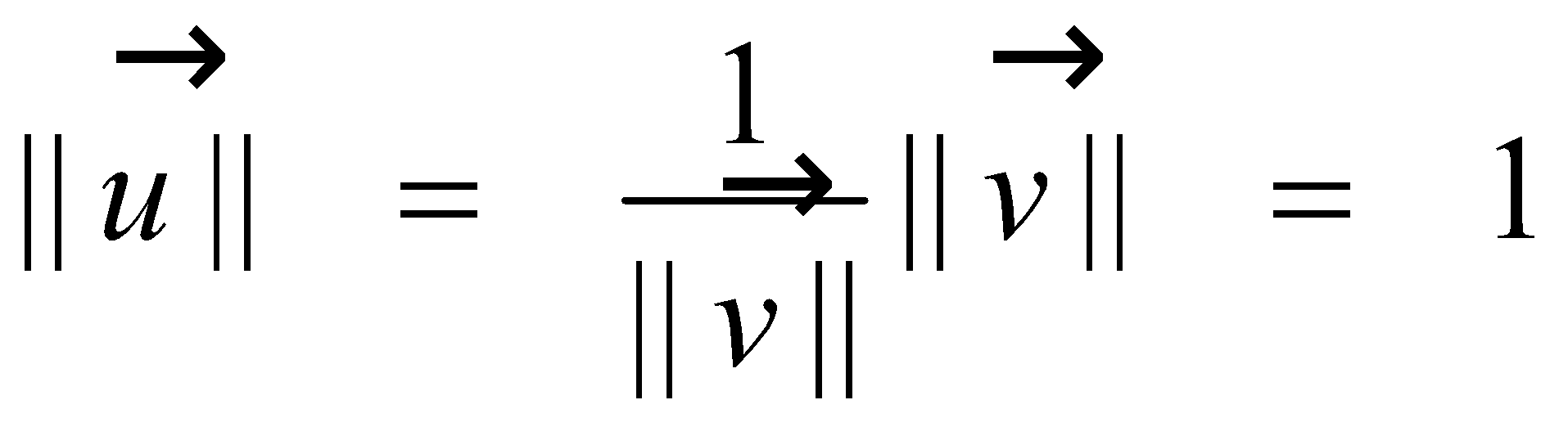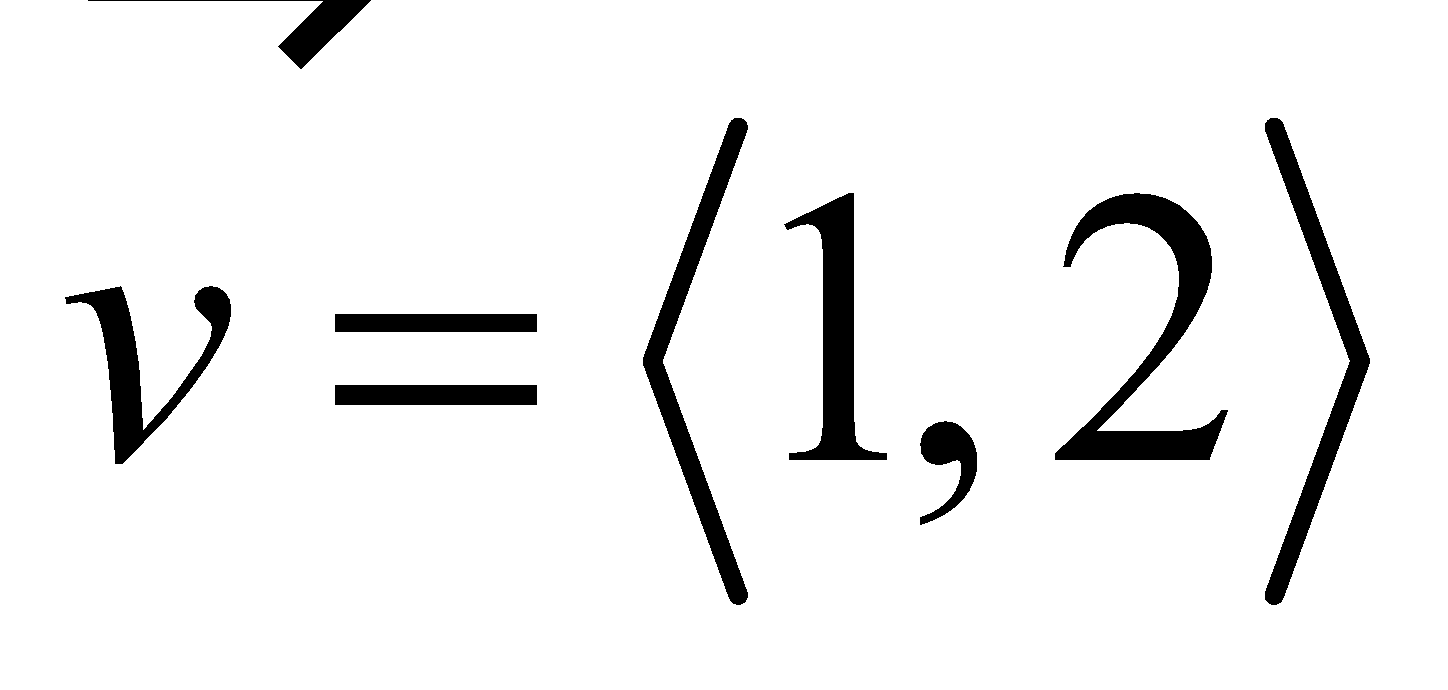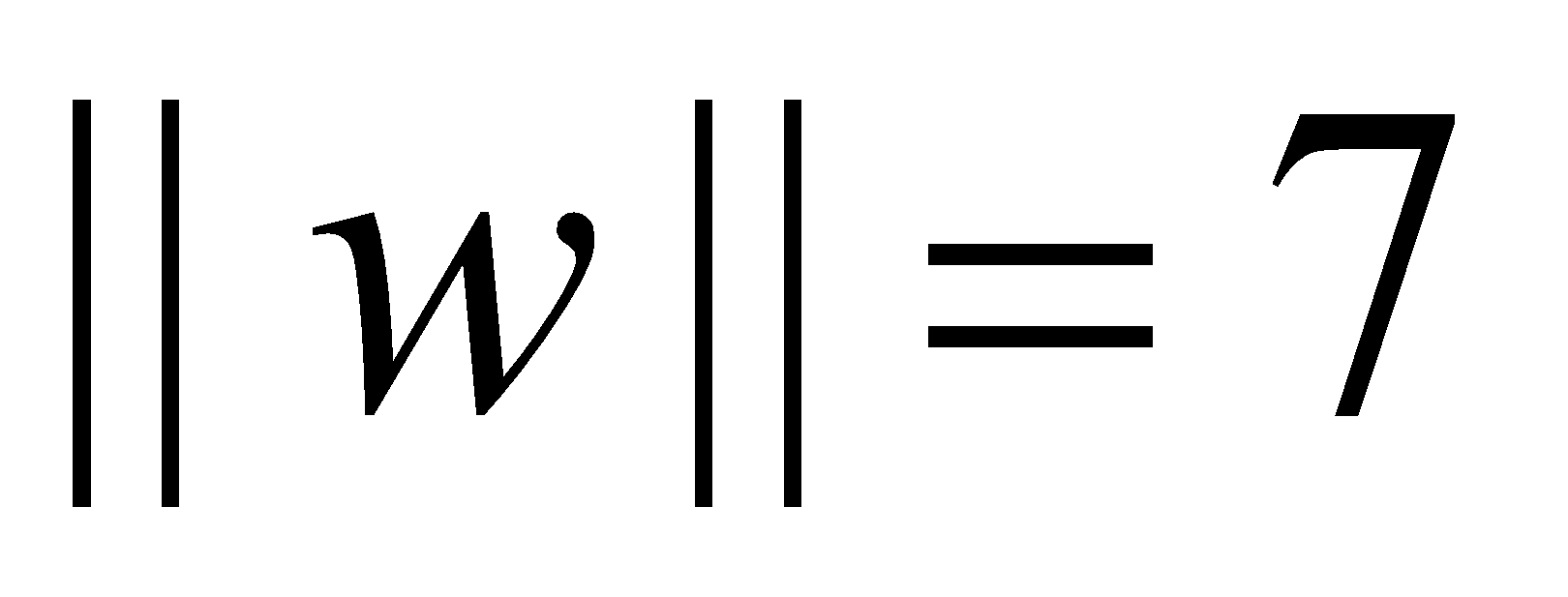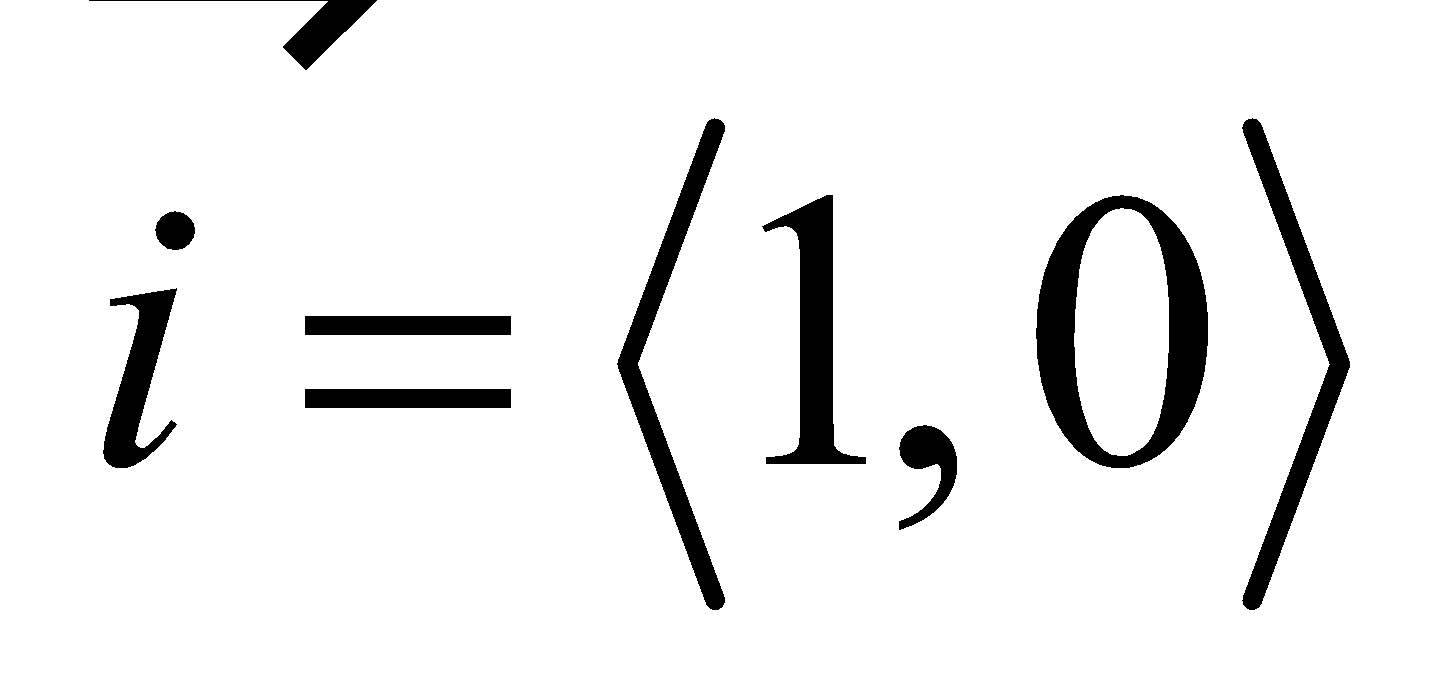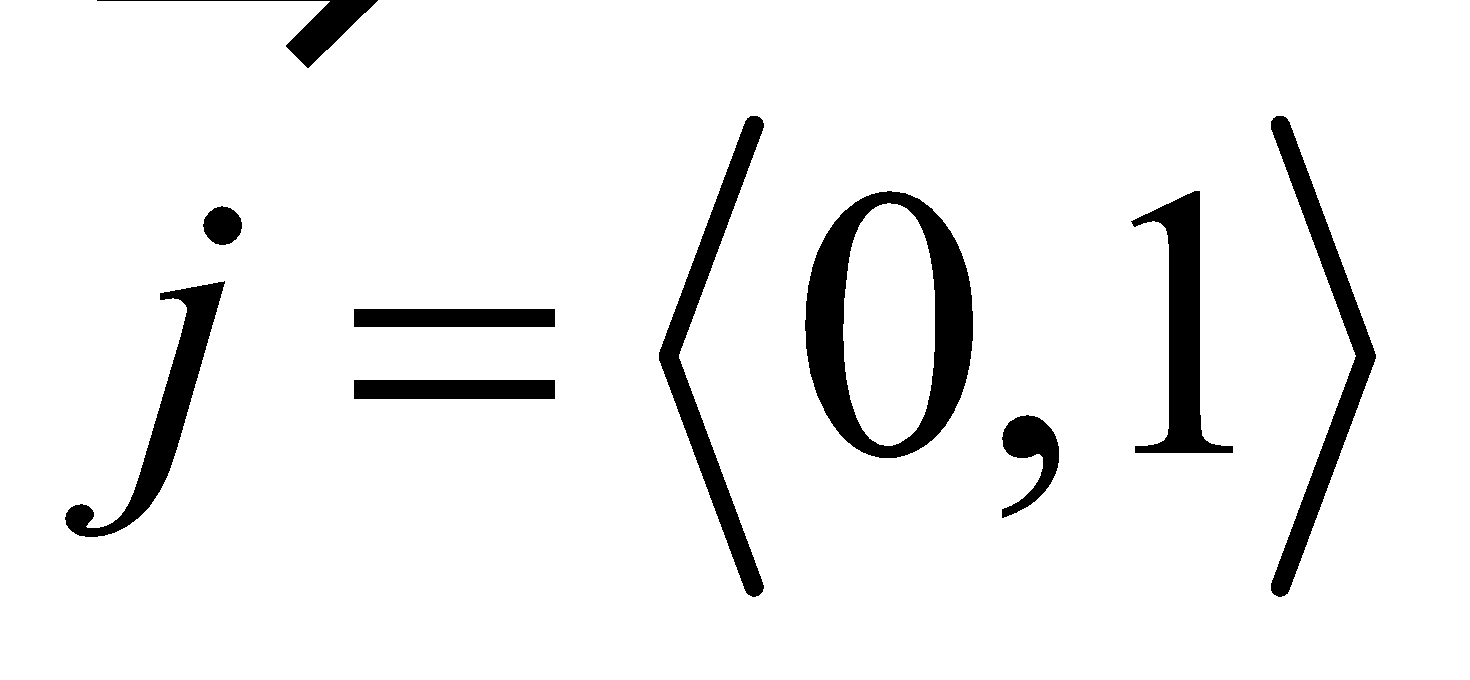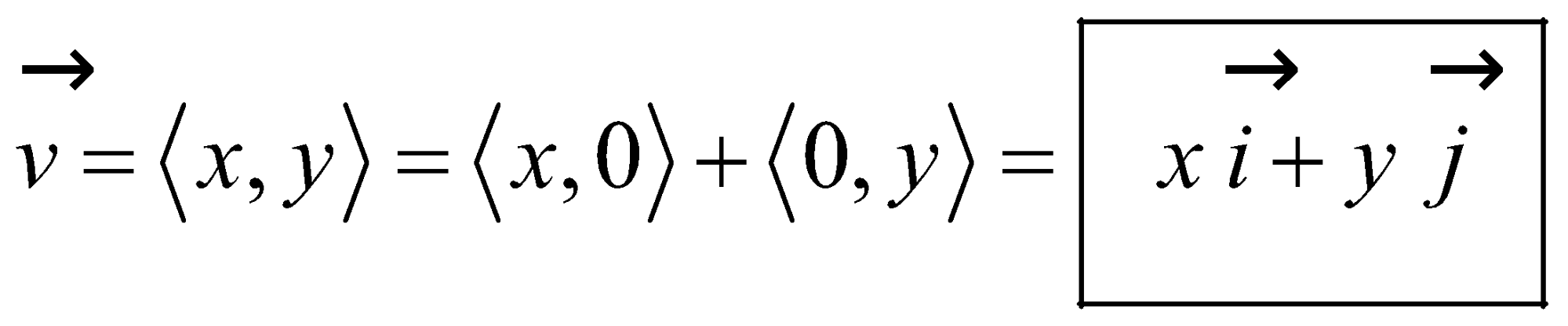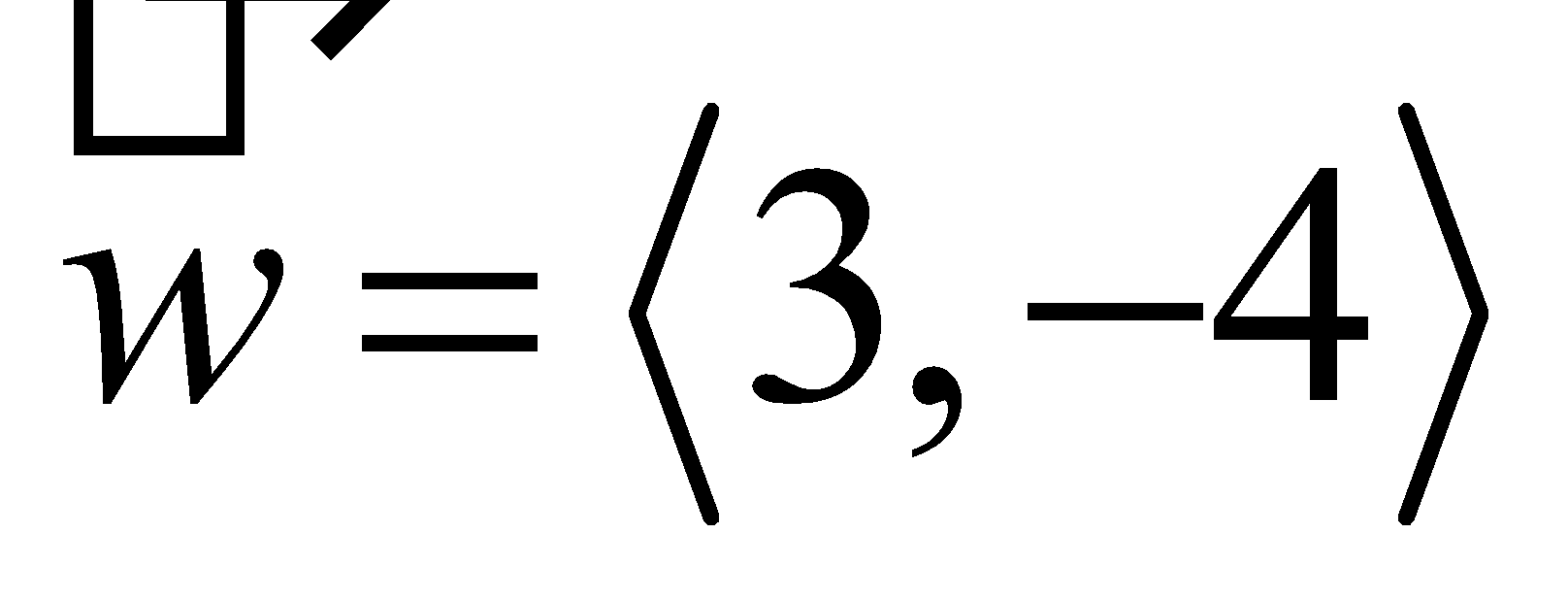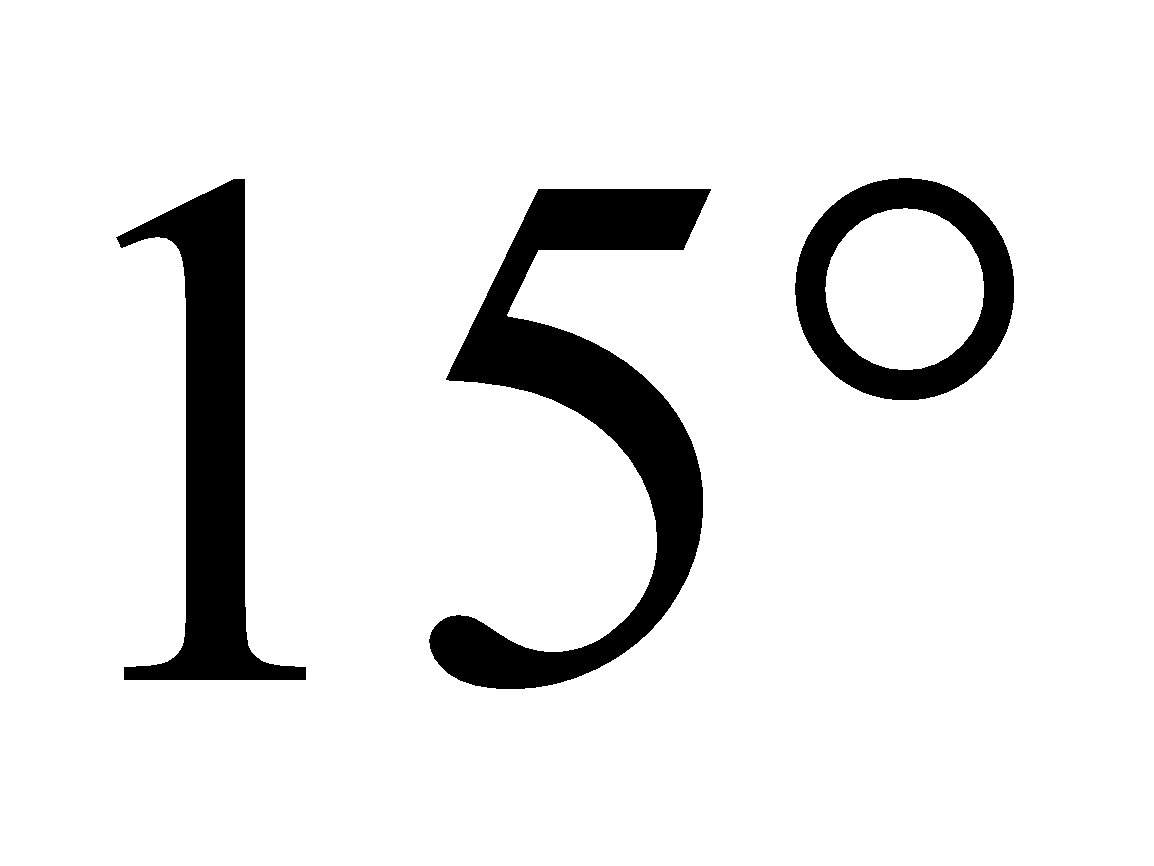Untitled Page 01
- Page ID
- 30083
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Vectors in Plane
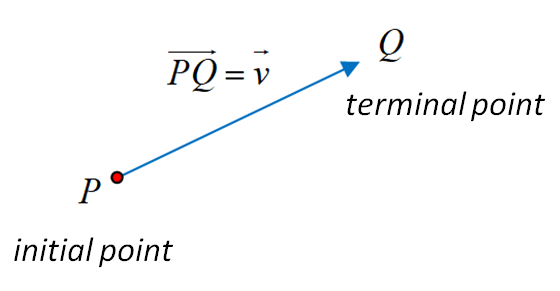
|
Vector |
|
Notation : draw an arrow above the name of the vector (or write in bold).
- the initial point - the terminal point
- the magnitude of the vector (length) |
|
|
Zero vector ( ) |
|
|
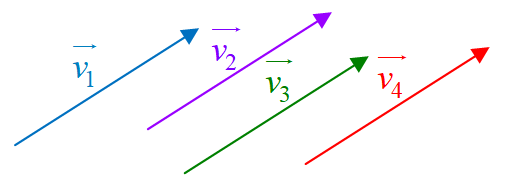
Parallel vectors |
|
|
Translation |
|
|
Equivalent vectors |
|
* Other common quantities that we encounter in mathematics and physics are scalars, which are simply numbers (so quantities that have only a value, a magnitude, but no direction).
Operations Involving Vectors
|
Multiplication of a vector by a scalar |
Scalar multiplication : The product of a scalar and a vector is a vector whose magnitude is times the magnitude of the original vector and depending on the sign of , the direction is:
If either or , then |
|
|
Sum of vectors |
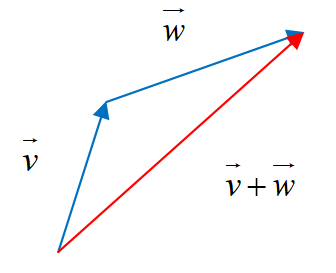
Vector addition |
|
|
Triangle Method: place the initial point of the second vector ( ) at the terminal point of the first vector ( ). The resultant vector representing the sum of the two vectors is then the vector whose initial point coincides with the initial point of and the terminal point coincides with the terminal point of .
|
|
|
|
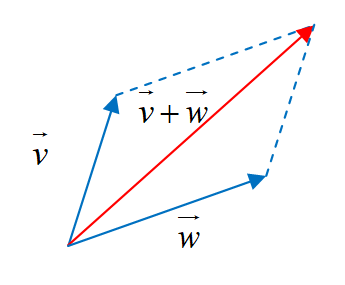
Parallelogram Method: place the two vectors so that they have the same initial point and then draw a parallelogram in which the two vectors form two adjacent sides. The sum of the two vectors is then the diagonal of the parallelogram as shown in the picture. |
|
|
|
Triangle Inequality |
In a triangle, the length of any one side is less than the sum of the lengths of the remaining sides.
Note : If the two vectors are parallel and point in the same direction, then the magnitude of the resultant vector equals the sum of the magnitudes of the two component vectors. |
|
|
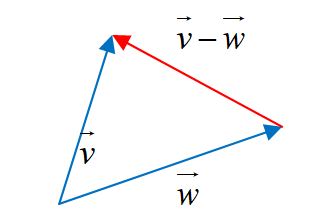
Difference of vectors |
Vector Subtraction: |
|
|
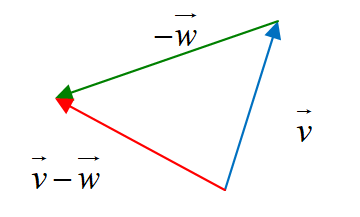
Triangle Method: The difference of two vectors is the vector from terminal point of to the terminal point of . |
|
|
|
Note: the vector difference is equivalent to the vector sum . This means we can add the vector with the opposite of the vector . |
|
|
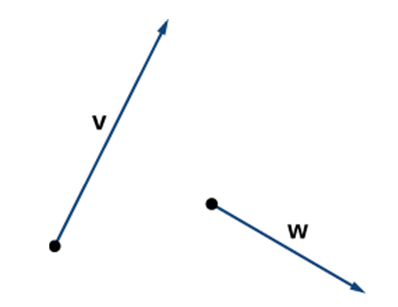
- (Example 2) Consider the vectors and . Sketch each of the stated vectors.
- (using the Triangle Rule)
- (using the Parallelogram Rule)
- (Example 3) Are and equivalent vectors?
has initial point (1, -4) and terminal point (1, 0).
|
has initial point (-2, 2) and terminal point (-1, 3).
|
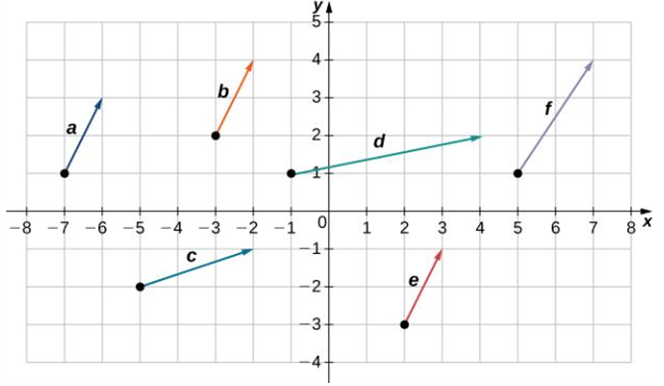
- (Exercise. 3) Which of the following vectors are equivalent?
- (Example 4) Express vector with initial point (-3, 4) and terminal point (1, 2) in component form.
Component Form of a Vector
|
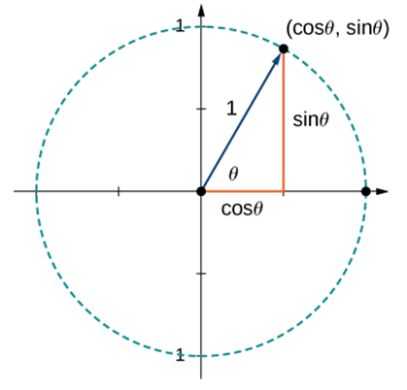
Standard-position vector (radius vector). |
- component in the direction of the -axis - component in the direction of the -axis |
|
|
Component form of an arbitrary vector |
|
|
|
Magnitude of a vector |
The magnitude of a standard-position vector is
|
|
|
The magnitude of is
|
||
|
Operations on Vectors in Component Form |
Let and be vectors, and let be a scalar.
|
|
|
Properties of Vector Operations |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
- (Example 5) Let be the vector with initial point (2, 5) and terminal point (8, 13) and let .
- Express in component form and find .
Using algebra, find
|
Finding the components |
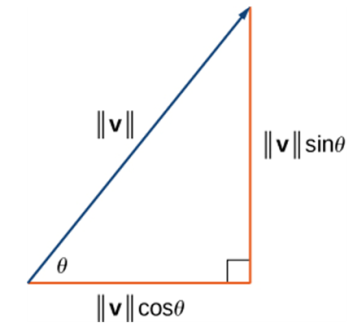
Given the magnitude and direction of a vector, we can find the Cartesian components of a vector:
- angle between the vector and the positive -axis |
|
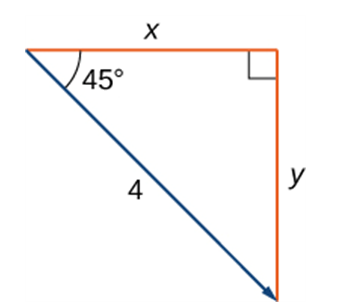
- (Example 6) Find the component form of a vector with magnitude 4 that forms an angle of with the -axis.
|
Unit vector |
Unit vector – a vector of unit length (magnitude of 1) in some given direction. |
|
|
For a nonzero vector , a unit vector in the same direction is obtained by scalar multiplication by the reciprocal of magnitude [1] :
|
|
|
|
Proof : For any scalar , we have . In this case , so . Therefore, . |
||
- (Example 7) Let .
- Find a unit vector with the same direction as .
- Find a vector with the same direction as such that .
|
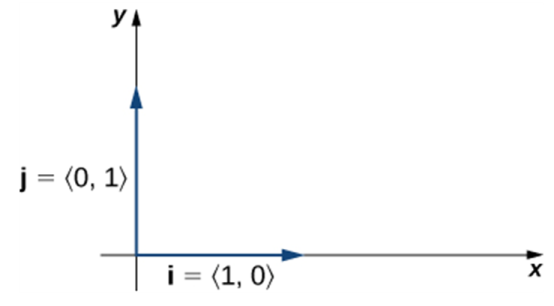
Standard unit vectors |
If we use the Cartesian (rectangular) coordinate system, the two components of a vector represent the horizontal and the vertical component of a vector, so it is convenient to use the standard unit vectors and .
Thus,
|
- (Example 8)
- Express the vector in terms of standard unit vectors.
- Vector is a unit vector that forms an angle of with the positive -axis. Express in terms of the standard unit vectors.
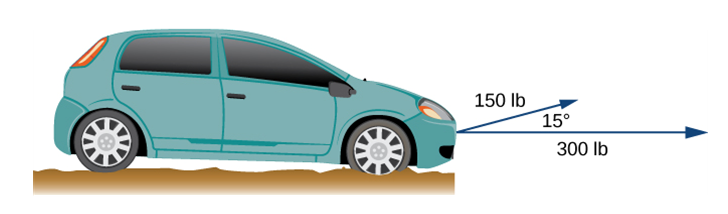
- (Example 9) Jane’s car is stuck in the mud. Lisa and Jed come along in a truck to help pull her out. They attach one end of a tow strap to the front of the car and the other end to the truck’s trailer hitch, and the truck starts to pull. Meanwhile, Jane and Jed get behind the car and push. The truck generates a horizontal force of 300 lb on the car. These forces can be represented as vectors. The angle between these vectors is . Find the resultant force (the vector sum) and give its magnitude to the nearest tenth of a pound and its direction angle with respect to the positive -axis.
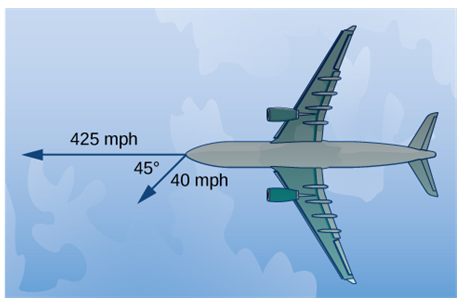
- (Example 10) An airplane flies dues west at an airspeed of 425 mph. The wind is blowing from the northeast at 40 mph. What is the ground speed of the airplane? What is the bearing of the airplane?
Reference :
- OpenStax, Calculus Volume 3, Gilbert Strang, Massachusetts Institute of Technology and Edwin “Jed” Herman, University of Wisconsin-Stevens Point. OpenStax CNX. Aug 28, 2019 http://cnx.org/contents/a31cd793-216...bbd76a5fa@5.30.
[1] The process of finding a unit vector in a given direction is called normalization .