12.3E: Exercises for Section 12.3

Last updated
Save as PDF

Page ID: 30613

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Motion in Space

1) Given $\vecs r(t)=(3t^2−2)\,\hat{\mathbf{i}}+(2t−\sin t)\,\hat{\mathbf{j}}$,

a. find the velocity of a particle moving along this curve.

b. find the acceleration of a particle moving along this curve.

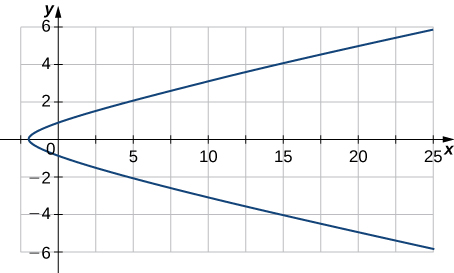
$CNX_Calc_Figure_13_04_205.jpg$

Answer:: a. $\vecs v(t)=6t\,\hat{\mathbf{i}}+(2−\cos t)\,\hat{\mathbf{i}}$
b. $\vecs a(t)=6\,\hat{\mathbf{i}}+\sin t\,\hat{\mathbf{i}}$

In questions 2 - 5, given the position function, find the velocity, acceleration, and speed in terms of the parameter $t$.

2) $\vecs r(t)=e^{−t}\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+\tan t\,\hat{\mathbf{k}}$

3) $\vecs r(t)=⟨3\cos t,\,3\sin t,\,t^2⟩$

Answer:: $\vecs v(t)=-3\sin t\,\hat{\mathbf{i}}+3\cos t\,\hat{\mathbf{j}}+2t\,\hat{\mathbf{k}}$
$\vecs a(t)=-3\cos t\,\hat{\mathbf{i}}-3\sin t\,\hat{\mathbf{j}}+2\,\hat{\mathbf{k}}$
$\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{9 + 4t^2}$

4) $\vecs r(t)=t^5\,\hat{\mathbf{i}}+(3t^2+2t- 5)\,\hat{\mathbf{j}}+(3t-1)\,\hat{\mathbf{k}}$

5) $\vecs r(t)=2\cos t\,\hat{\mathbf{j}}+3\sin t\,\hat{\mathbf{k}}$. The graph is shown here:

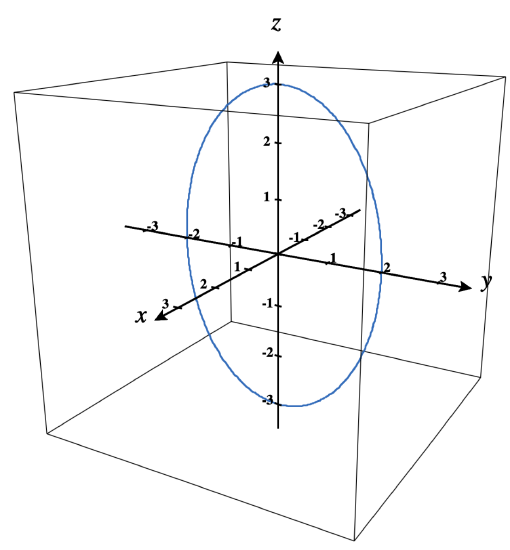
Answer:: $\vecs v(t)=-2\sin t\,\hat{\mathbf{j}}+3\cos t\,\hat{\mathbf{k}}$
$\vecs a(t)=-2\cos t\,\hat{\mathbf{j}}-3\sin t\,\hat{\mathbf{k}}$
$\text{Speed}(t) = \|\vecs v(t)\| = \sqrt{4\sin^2 t+9\cos^2 t}=\sqrt{4+5\cos^2 t}$

In questions 6 - 8, find the velocity, acceleration, and speed of a particle with the given position function.

6) $\vecs r(t)=⟨t^2−1,t⟩$

7) $\vecs r(t)=⟨e^t,e^{−t}⟩$

Answer:: $\vecs v(t)=⟨e^t,−e^{−t}⟩$,
$\vecs a(t)=⟨e^t, e^{−t}⟩,$
$ \|\vecs v(t)\| = \sqrt{e^{2t}+e^{−2t}}$

8) $\vecs r(t)=⟨\sin t,t,\cos t⟩$. The graph is shown here:

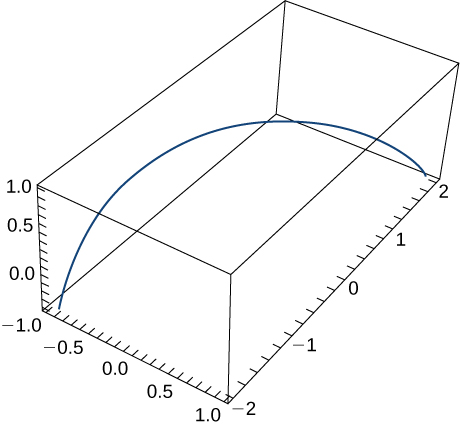
$CNX_Calc_Figure_13_04_207.jpg$

9) The position function of an object is given by $\vecs r(t)=⟨t^2,5t,t^2−16t⟩$. At what time is the speed a minimum?

Answer:: $t = 4$

10) Let $\vecs r(t)=r\cosh(ωt)\,\hat{\mathbf{i}}+r\sinh(ωt)\,\hat{\mathbf{j}}$. Find the velocity and acceleration vectors and show that the acceleration is proportional to $\vecs r(t)$.

11) Consider the motion of a point on the circumference of a rolling circle. As the circle rolls, it generates the cycloid $\vecs r(t)=(ωt−\sin(ωt))\,\hat{\mathbf{i}}+(1−\cos(ωt))\,\hat{\mathbf{j}}$, where $\omega$ is the angular velocity of the circle and $b$ is the radius of the circle:

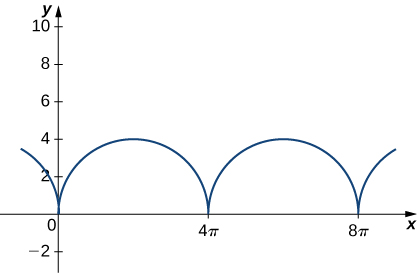
$CNX_Calc_Figure_13_04_201.jpg$

Find the equations for the velocity, acceleration, and speed of the particle at any time.

Answer:: $\vecs v(t)=(ω−ω\cos(ωt))\,\hat{\mathbf{i}}+(ω\sin(ωt))\,\hat{\mathbf{j}}$
$\vecs a(t)=(ω^2\sin(ωt))\,\hat{\mathbf{i}}+(ω^2\cos(ωt))\,\hat{\mathbf{j}}$
$\begin{align*} \text{speed}(t) &= \sqrt{(ω−ω\cos(ωt))^2 + (ω\sin(ωt))^2} \\
&= \sqrt{ω^2 - 2ω^2 \cos(ωt) + ω^2\cos^2(ωt) + ω^2\sin^2(ωt)} \\
&= \sqrt{2ω^2(1 - \cos(ωt))} \end{align*} $

12) A person on a hang glider is spiraling upward as a result of the rapidly rising air on a path having position vector $\vecs r(t)=(3\cos t)\,\hat{\mathbf{i}}+(3\sin t)\,\hat{\mathbf{j}}+t^2\,\hat{\mathbf{k}}$. The path is similar to that of a helix, although it is not a helix. The graph is shown here:

$CNX_Calc_Figure_13_04_208.jpg$

Find the following quantities:

a. The velocity and acceleration vectors

b. The glider’s speed at any time

Answer:: $\|\vecs v(t)\|=\sqrt{9+4t^2}$

c. The times, if any, at which the glider’s acceleration is orthogonal to its velocity

13) Given that $\vecs r(t)=⟨e^{−5t}\sin t,\, e^{−5t}\cos t,\, 4e^{−5t}⟩$ is the position vector of a moving particle, find the following quantities:

a. The velocity of the particle

Answer:: $\vecs v(t)=⟨e^{−5t}(\cos t−5\sin t),\, −e^{−5t}(\sin t+5\cos t),\, −20e^{−5t}⟩$

b. The speed of the particle

c. The acceleration of the particle

Answer:: $\vecs a(t)=⟨e^{−5t}(−\sin t−5\cos t)−5e^{−5t}(\cos t−5\sin t), \; −e^{−5t}(\cos t−5\sin t)+5e^{−5t}(\sin t+5\cos t),\; 100e^{−5t}⟩$

14) Find the maximum speed of a point on the circumference of an automobile tire of radius $1$ ft when the automobile is traveling at $55$ mph.

15) Find the position vector-valued function $\vecs r(t)$, given that $\vecs a(t)=\hat{\mathbf{i}}+e^t \,\hat{\mathbf{j}}, \quad \vecs v(0)=2\,\hat{\mathbf{j}}$, and $\vecs r(0)=2\,\hat{\mathbf{i}}$.

16) Find $\vecs r(t)$ given that $\vecs a(t)=−32\,\hat{\mathbf{j}}, \vecs v(0)=600\sqrt{3} \,\hat{\mathbf{i}}+600\,\hat{\mathbf{j}}$, and $\vecs r(0)=\vecs 0$.

17) The acceleration of an object is given by $\vecs a(t)=t\,\hat{\mathbf{j}}+t\,\hat{\mathbf{k}}$. The velocity at $t=1$ sec is $\vecs v(1)=5\,\hat{\mathbf{j}}$ and the position of the object at $t=1$ sec is $\vecs r(1)=0\,\hat{\mathbf{i}}+0\,\hat{\mathbf{j}}+0\,\hat{\mathbf{k}}$. Find the object’s position at any time.

Answer:: $\vecs r(t)=0\,\hat{\mathbf{i}}+\left(\frac{1}{6}t^3+4.5t−\frac{14}{3}\right)\,\hat{\mathbf{j}}+\left(\frac{1}{6}t^3−\frac{1}{2}t+\frac{1}{3}\right)\,\hat{\mathbf{k}}$

Projectile Motion

18) A projectile is shot in the air from ground level with an initial velocity of $500$ m/sec at an angle of 60° with the horizontal.

a. At what time does the projectile reach maximum height?

Answer:: $44.185$ sec

b. What is the approximate maximum height of the projectile?

c. At what time is the maximum range of the projectile attained?

Answer:: $t=88.37$ sec

d. What is the maximum range?

e. What is the total flight time of the projectile?

Answer:: $t=88.37$ sec

19) A projectile is fired at a height of $1.5$ m above the ground with an initial velocity of $100$ m/sec and at an angle of 30° above the horizontal. Use this information to answer the following questions:

a. Determine the maximum height of the projectile.

b. Determine the range of the projectile.

Answer:: The range is approximately $886.29$ m.

20) A golf ball is hit in a horizontal direction off the top edge of a building that is 100 ft tall. How fast must the ball be launched to land $450$ ft away?

21) A projectile is fired from ground level at an angle of 8° with the horizontal. The projectile is to have a range of $50$ m. Find the minimum velocity (speed) necessary to achieve this range.

Answer:: $v=42.16$ m/sec

22) Prove that an object moving in a straight line at a constant speed has an acceleration of zero.

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.