13.1E: Functions of Multiple Variables (Exercises)

Last updated
Save as PDF

Page ID: 30623

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

For the following exercises, evaluate each function at the indicated values.

1) $ W(x,y)=4x^2+y^2.$ Find $ W(2,−1), W(−3,6)$.

Answer: $ W(2,−1) = 17,\quad W(−3,6) = 72$

2) $ W(x,y)=4x^2+y^2$. Find $ W(2+h,3+h).$

3) The volume of a right circular cylinder is calculated by a function of two variables, $ V(x,y)=πx^2y,$ where $ x$ is the radius of the right circular cylinder and $ y$ represents the height of the cylinder. Evaluate $ V(2,5)$ and explain what this means.

Answer: $ V(2,5) = 20π\,\text{units}^3$ This is the volume when the radius is $ 2$ and the height is $ 5$.

4) An oxygen tank is constructed of a right cylinder of height $ y$ and radius $ x$ with two hemispheres of radius $ x$ mounted on the top and bottom of the cylinder. Express the volume of the cylinder as a function of two variables, $ x$ and $ y$, find $ V(10,2)$, and explain what this means.

For exercises 5 - 10, find the domain and range of the given function. State the domain in set-builder notation and the range in interval notation.

5) $ V(x,y)=4x^2+y^2$

Answer: Domain: $\big\{(x, y) \, | \, x \in \rm I\!R, y \in \rm I\!R\big\}$ That is, all points in the $xy$-plane
Range: $ [0, \infty) $

6) $ f(x,y)=\sqrt{x^2+y^2−4}$

Answer: Domain: $ \big\{(x, y) \, | \, x^2+y^2 \ge 4\big\}$
Range: $ [0, \infty) $

7) $ f(x,y)=4\ln(y^2−x)$

Answer: Domain: $ \big\{(x, y) \, | \, x<y^2 \big\}$
Range: $ (-\infty, \infty) $

8) $ g(x,y)=\sqrt{16−4x^2−y^2}$

Answer: Domain: $ \big\{(x, y) \, | \, \dfrac{x^2}{4} + \dfrac{y^2}{16} \le 1\big\}$
Range: $ [0, 4] $

9) $ z=\arccos(y−x)$

Answer: Domain: $ \big\{(x, y) \, | \, x - 1 \le y \le x + 1\big\}$ That is, all points between the graphs of $y = x -1$ and $y = x +1 $.
Range: $ [0, \pi] $

10) $ f(x,y)=\dfrac{y+2}{x^2}$

Answer: Domain: $ \big\{(x, y) \, | \, x\neq 0 \big\}$
Range: $ (-\infty, \infty) $

Find the range of the functions.

11) $ g(x,y)=\sqrt{16−4x^2−y^2}$

Answer: $ \big\{z \, | \, 0≤z≤4\big\}$ or in interval notation: $[0,4]$

12) $ V(x,y)=4x^2+y^2$

13) $ z=y^2−x^2$

Answer: The set $\rm I\!R$

In exercises 14 - 29, find the level curves of each function at the indicated values of $ c$ to visualize the given function. Sketch a contour plot for those exercises where you are asked for more than 3 values of $c$.

14) $ z(x,y)=y^2−x^2, \quad c=1$

15) $ z(x,y)=y^2−x^2,\quad c=4$

Answer: $ y^2−x^2=4,$ a hyperbola

16) $ g(x,y)=x^2+y^2;\quad c=0, 1, 2, 3, 4, 9$

17) $ g(x,y)=4−x−y;\quad c=0,1, 2, 3, 4$

Answer: Level curves are lines with $ y = -x + (4 - c) $.
For each value of $c$ these are:
$ c = 0: \, y = -x + 4$,
$ c = 1: \, y = -x + 3$,
$ c = 2: \, y = -x + 2$,
$ c = 3: \, y = -x + 1$,
$ c = 4: \, y = -x $.
The contour plot consists of a series of parallel lines.
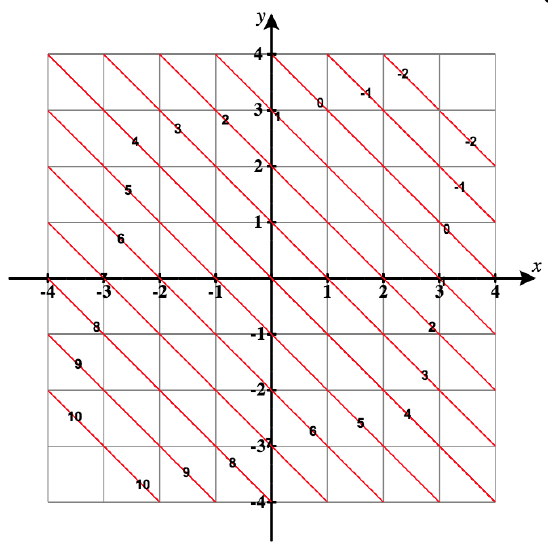
$Contour plot of the function g(x,y)=4−x−y$

18) $ f(x,y)=xy;c=1;\quad c=−1$

19) $ h(x,y)=2x−y;\quad c=-2,0,2$

Answer: $ 2x−y=0,2x−y=−2,2x−y=2;$ three lines

20) $ f(x,y)=x^2−y;\quad c=1,2$

21) $ g(x,y)=\dfrac{x}{x+y};c=−1,0,1,2$

Answer: Level curves are lines with the form $ y = x \left( \dfrac{1-c}{c} \right) $. At $c = 0$, we solve it directly from the equation $\dfrac{x}{x+y}=0$ to get $x = 0$.
For each value of $c$ these are:
$ c = -1: \, y = -2x$,
$ c = 0: \, x = 0,\text{ with }y \ne 0$,
$ c = 1: \, y = 0,\text{ with }x \ne 0$,
$ c = 2: \, y = -\frac{1}{2}x$.
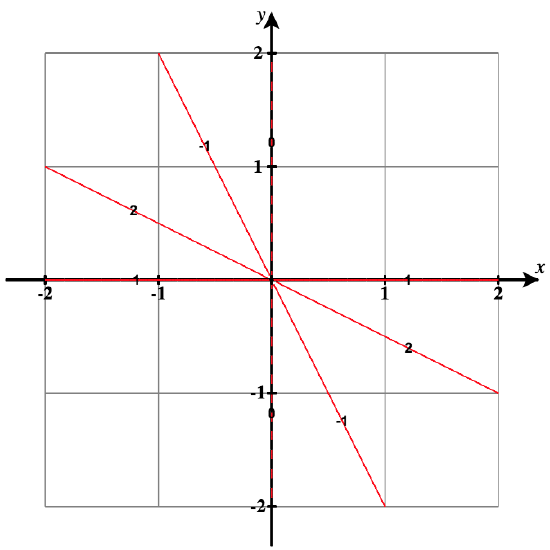
$Contour Plot of the function g(x, y) = x/(x+y)$

22) $ g(x,y)=x^3−y;\quad c=−1,0,2$

23) $ g(x,y)=e^{xy};\quad c=\frac{1}{2},3$

Answer: The level curves have the form, $ y = \dfrac{\ln c}{x}$.
For each value of $c$ these are:
$ c = \frac{1}{2}: \, y = \dfrac{\ln \frac{1}{2}}{x}$ that can be rewritten as, $y = -\dfrac{\ln 2}{x}$

$ c = 3: \, y = \dfrac{\ln 3}{x}$.

24) $ f(x,y)=x^2;\quad c=4,9$

25) $ f(x,y)=xy−x;\quad c=−2,0,2$

Answer: Level curves have the form: $ y = \dfrac{c}{x} + 1$.
Here $y = \dfrac{-2}{x} + 1,\quad y = 1,\quad y = \dfrac{2}{x} + 1$ or $ xy−x=−2,\,xy−x=0,\,xy−x=2$

26) $ h(x,y)=\ln(x^2+y^2);\quad c=−1,0,1$

27) $ g(x,y)=\ln\left(\dfrac{y}{x^2}\right);\quad c=−2,0,2$

Answer: The level curves have the form, $ y =e^c x^2$.
For each value of $c$ these are:
$ c = -2: \, y = e^{-2} x^2 $,
$ c = 0: \, y = x^2 $,
$ c = 2: \, y = e^{2} x^2 $.

28) $ z=f(x,y)=\sqrt{x^2+y^2},\quad c=3$

29) $ f(x,y)=\dfrac{y+2}{x^2},\quad c=$ any constant

Answer: The level curves are parabolas of the form $ y=cx^2−2,\text{ with }x \ne 0$.
$Contour plot of the function f(x, y) = (y + 2)/x^2$

In exercises 30-32, find the vertical traces of the functions at the indicated values of $ x$ and $ y$, and plot the traces.

30) $ z=4−x−y, \quad x=2$

31) $ f(x,y)=3x+y^3, \quad x=1$

Answer

$ z=3+y^3,$ a curve in the $zy$-plane with rulings parallel to the $x$-axis

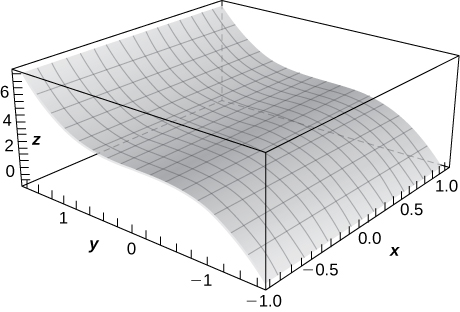
$Surface plot of the function f(x,y)=3x+y^3$

32) $ z=\cos\sqrt{x^2+y^2}, \quad x=1$

In exercises 33 - 38, find the domain and range of each function.

33) $ z=\sqrt{100−4x^2−25y^2}$

Answer: Domain: $ \big\{(x, y) \, | \, \dfrac{x^2}{25}+\dfrac{y^2}{4}≤1\big\}$
Range: $ [0, 10] $

34) $ z=\ln(x−y^2)$

35) $ f(x,y,z)=\dfrac{1}{\sqrt{36−4x^2−9y^2−z^2}}$

Answer: Domain: $ \big\{(x, y, z) \, | \, \dfrac{x^2}{9}+\dfrac{y^2}{4}+\dfrac{z^2}{36}<1\big\}$
Range: $ \big[\frac{1}{6}, \infty\big) $

36) $ f(x,y,z)=\sqrt{49−x^2−y^2−z^2}$

37) $ f(x,y,z)=\sqrt[3]{16−x^2−y^2−z^2}$

Answer: Domain: All points in $ xyz$-space
Range: $ \big(-\infty, \sqrt[3]{16}\,\big] $

38) $ f(x,y)=\cos\sqrt{x^2+y^2}$

In exercises 39 - 40, plot a graph of the function.

39) $ z=f(x,y)=\sqrt{x^2+y^2}$

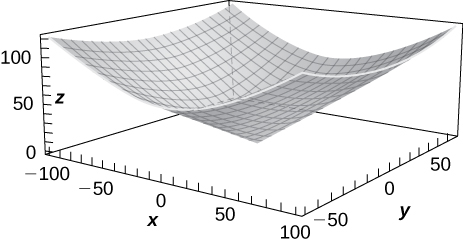
Answer: $Surface plot of the surface f(x,y)=sqrt(x^2+y^2)$

40) $ z=x^2+y^2$

41) Use technology to graph $ z=x^2y.$

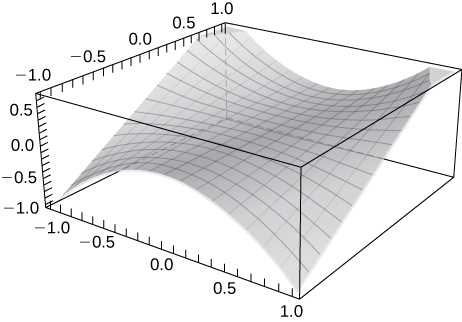
Answer: $Surface plot of the function z=x^2y$

In exercises 42 - 46, sketch the function by finding its level curves. Verify the graph using technology, such as CalcPlot3D.

42) $ f(x,y)=\sqrt{4−x^2−y^2}$

43) $ f(x,y)=2−\sqrt{x^2+y^2}$

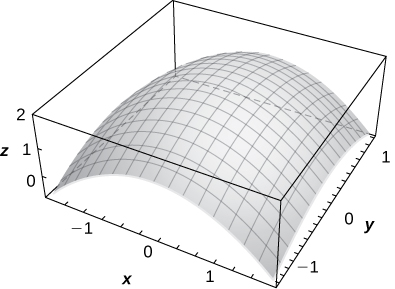
Answer: $Surface plot of the function f(x,y)=2−sqrt(x^2+y^2)$

44) $ z=1+e^{−x^2−y^2}$

45) $ z=\cos\sqrt{x^2+y^2}$

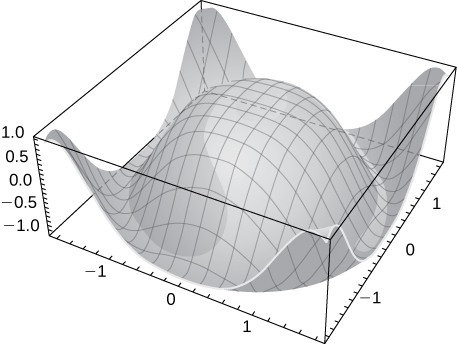
Answer: $Surface plot of the function z=cos(sqrt(x^2+y^2))$

46) $ z=y^2−x^2$

47) Describe the contour lines for several values of $ c$ for $ z=x^2+y^2−2x−2y.$

Answer: The contour lines are concentric circles centered at the point, $ (1, 1) $.
You can see this by completing the square after setting this function equal to $c$.
That is, we write $ x^2-2x+1+y^2−2y+1 = c + 2 $ which can be rewritten as, $ (x - 1)^2 + (y - 1)^2 = c + 2 $.
This gives us circles centered at the point, $ (1, 1) $, each with a radius of $ \sqrt{c+2} $.

In exercises, 48 - 52, find the level surface for the given value of $c$ for each function of three variables and describe it.

48) $ w(x,y,z)=x−2y+z,\quad c=4$

49) $ w(x,y,z)=x^2+y^2+z^2,\quad c=9$

Answer: $ x^2+y^2+z^2=9$, a sphere of radius $ 3$

50) $ w(x,y,z)=x^2+y^2−z^2,\quad c=−4$

51) $ w(x,y,z)=x^2+y^2−z^2,\quad c=4$

Answer: $ x^2+y^2−z^2=4,$ a hyperboloid of one sheet

52) $ w(x,y,z)=9x^2−4y^2+36z^2,\quad c=0$

In exercises 53 - 55, find an equation of the level curve of $ f$ that contains the point $ P$.

53) $ f(x,y)=1−4x^2−y^2,\quad P(0,1)$

Answer: $ 4x^2+y^2=1,$

54) $ g(x,y)=y^2\arctan x,\quad P(1,2)$

55) $ g(x,y)=e^{xy}(x^2+y^2),\quad P(1,0)$

Answer: $ 1=e^{xy}(x^2+y^2)$

56) The strength $ E$ of an electric field at point $ (x,y,z)$ resulting from an infinitely long charged wire lying along the $y$-axis is given by $ E(x,y,z)=k/\sqrt{x^2+y^2}$, where $ k$ is a positive constant. For simplicity, let $ k=1$ and find the equations of the level surfaces for $ E=10$ and $ E=100.$

57) A thin plate made of iron is located in the $xy$-plane The temperature $ T$ in degrees Celsius at a point $ P(x,y)$ is inversely proportional to the square of its distance from the origin. Express $ T$ as a function of $ x$ and $ y$.

Answer: $ T(x,y)=\dfrac{k}{x^2+y^2}$

58) Refer to the preceding problem. Using the temperature function found there, determine the proportionality constant if the temperature at point $ P(1,2)$ is $ 50°C.$ Use this constant to determine the temperature at point $ Q(3,4).$

59) Refer to the preceding problem. Find the level curves for $ T=40°C$ and $ T=100°C,$ and describe what the level curves represent.

Answer: $ x^2+y^2=\dfrac{k}{40}, \quad x^2+y^2=\dfrac{k}{100}$. The level curves represent circles of radii $ \sqrt{10k}/20$ and $ \sqrt{k}/10$

Contributors

Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
Paul Seeburger (Monroe Community College) added the contour plots to answers for problems 17, 21 and 29.