14.2b: Double Integrals Over General Regions
- Last updated
- Save as PDF
- Page ID
- 30647
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Recognize when a function of two variables is integrable over a general region.
- Evaluate a double integral by computing an iterated integral over a region bounded by two vertical lines and two functions of \(x\), or two horizontal lines and two functions of \(y\).
- Simplify the calculation of an iterated integral by changing the order of integration.
- Use double integrals to calculate the volume of a region between two surfaces or the area of a plane region.
- Solve problems involving double improper integrals.
Previously, we studied the concept of double integrals and examined the tools needed to compute them. We learned techniques and properties to integrate functions of two variables over rectangular regions. We also discussed several applications, such as finding the volume bounded above by a function over a rectangular region, finding area by integration, and calculating the average value of a function of two variables.
In this section we consider double integrals of functions defined over a general bounded region \(D\) on the plane. Most of the previous results hold in this situation as well, but some techniques need to be extended to cover this more general case.
General Regions of Integration
An example of a general bounded region \(D\) on a plane is shown in Figure \(\PageIndex{1}\). Since \(D\) is bounded on the plane, there must exist a rectangular region \(R\) on the same plane that encloses the region \(D\) that is, a rectangular region \(R\) exists such that \(D\) is a subset of \(R (D \subseteq R)\).
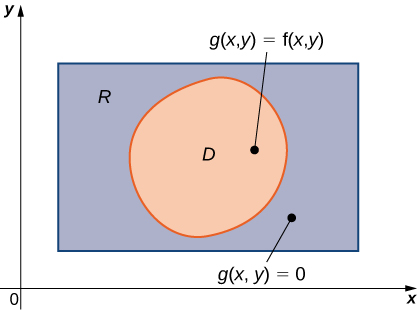
Suppose \(z = f(x,y)\) is defined on a general planar bounded region \(D\) as in Figure \(\PageIndex{1}\). In order to develop double integrals of \(f\) over \(D\) we extend the definition of the function to include all points on the rectangular region \(R\) and then use the concepts and tools from the preceding section. But how do we extend the definition of \(f\) to include all the points on \(R\)? We do this by defining a new function \(g(x,y)\) on \(R\) as follows:
\[g(x,y) = \begin{cases} f(x,y), & \text{if} \; (x,y) \; \text{is in}\; D \\[4pt] 0, & \text{if} \;(x,y) \; \text{is in} \; R \;\text{but not in}\; D \end{cases} \nonumber \]
Note that we might have some technical difficulties if the boundary of \(D\) is complicated. So we assume the boundary to be a piecewise smooth and continuous simple closed curve. Also, since all the results developed in the section on Double Integrals over Rectangular Regions used an integrable function \(f(x,y)\) we must be careful about \(g(x,y)\) and verify that \(g(x,y)\) is an integrable function over the rectangular region \(R\). This happens as long as the region \(D\) is bounded by simple closed curves. For now we will concentrate on the descriptions of the regions rather than the function and extend our theory appropriately for integration.
We consider two types of planar bounded regions.
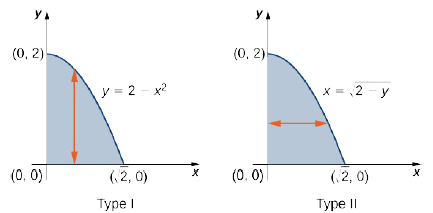
Definition: Type I and Type II regions
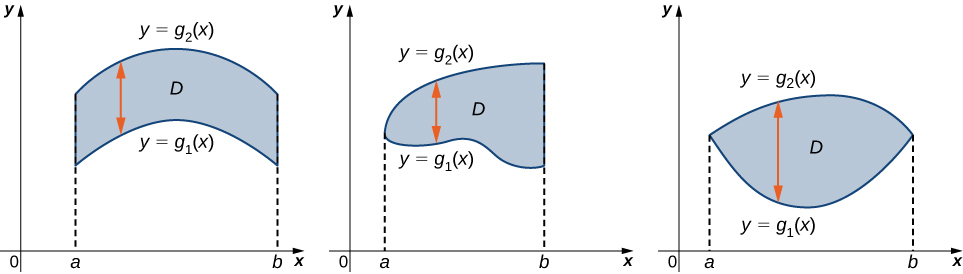
A region \(D\) in the \((x,y)\)-plane is of Type I if it lies between two vertical lines and the graphs of two continuous functions \(g_1(x)\) and \(g_2(x)\). That is (Figure \(\PageIndex{2}\)),
\[D = \big\{(x,y)\,|\, a \leq x \leq b, \space g_1(x) \leq y \leq g_2(x) \big\}. \nonumber \]
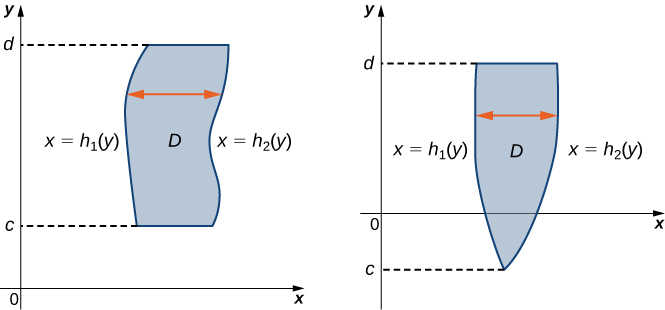
A region \(D\) in the \(xy\)-plane is of Type II if it lies between two horizontal lines and the graphs of two continuous functions \(h_1(y)\) and \(h_2(y)\). That is (Figure \(\PageIndex{3}\)),
\[D = \big\{(x,y)\,| \, c \leq y \leq d, \space h_1(y) \leq x \leq h_2(y) \big\}. \nonumber \]
Example \(\PageIndex{1}\): Describing a Region as Type I and Also as Type II
Consider the region in the first quadrant between the functions \(y = \sqrt{x}\) and \(y = x^3\) (Figure \(\PageIndex{4}\)). Describe the region first as Type I and then as Type II.
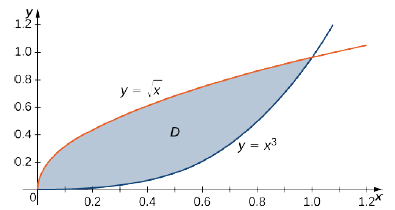
When describing a region as Type I, we need to identify the function that lies above the region and the function that lies below the region. Here, region \(D\) is bounded above by \(y = \sqrt{x}\) and below by \(y = x^3\) in the interval for \(x\) in \([0,1]\). Hence, as Type I, \(D\) is described as the set \(\big\{(x,y)\,| \, 0 \leq x \leq 1, \space x^3 \leq y \leq \sqrt[3]{x}\big\}\).
However, when describing a region as Type II, we need to identify the function that lies on the left of the region and the function that lies on the right of the region. Here, the region \(D\) is bounded on the left by \(x = y^2\) and on the right by \(x = \sqrt[3]{y}\) in the interval for \(y\) in \([0,1]\). Hence, as Type II, \(D\) is described as the set \(\big\{(x,y) \,| \, 0 \leq y \leq 1, \space y^2 \leq x \leq \sqrt[3]{y}\big\}\).
Exercise \(\PageIndex{1}\)
Consider the region in the first quadrant between the functions \(y = 2x\) and \(y = x^2\). Describe the region first as Type I and then as Type II.
- Hint
-
Graph the functions, and draw vertical and horizontal lines.
- Answer
-
Type I and Type II are expressed as \(\big\{(x,y) \,|\, 0 \leq x \leq 2, \space x^2 \leq y \leq 2x\big\}\) and \(\big\{(x,y)|\, 0 \leq y \leq 4, \space \frac{1}{2} y \leq x \leq \sqrt{y}\big\}\), respectively.
Double Integrals over Non-rectangular Regions
To develop the concept and tools for evaluation of a double integral over a general, nonrectangular region, we need to first understand the region and be able to express it as Type I or Type II or a combination of both. Without understanding the regions, we will not be able to decide the limits of integrations in double integrals. As a first step, let us look at the following theorem.
Theorem: Double Integrals over Nonrectangular Regions
Suppose \(g(x,y)\) is the extension to the rectangle \(R\) of the function \(f(x,y)\) defined on the regions \(D\) and \(R\) as shown in Figure \(\PageIndex{1}\) inside \(R\). Then \(g(x,y)\) is integrable and we define the double integral of \(f(x,y)\) over \(D\) by
\[\iint\limits_D f(x,y) \,dA = \iint\limits_R g(x,y) \,dA. \nonumber \]
The right-hand side of this equation is what we have seen before, so this theorem is reasonable because \(R\) is a rectangle and \(\iint\limits_R g(x,y)dA\) has been discussed in the preceding section. Also, the equality works because the values of \(g(x,y)\) are \(0\) for any point \((x,y)\) that lies outside \(D\) and hence these points do not add anything to the integral. However, it is important that the rectangle \(R\) contains the region \(D\).
As a matter of fact, if the region \(D\) is bounded by smooth curves on a plane and we are able to describe it as Type I or Type II or a mix of both, then we can use the following theorem and not have to find a rectangle \(R\) containing the region.
Theorem: Fubini’s Theorem (Strong Form)
For a function \(f(x,y)\) that is continuous on a region \(D\) of Type I, we have
\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y)\,dy \right] dx. \nonumber \]
Similarly, for a function \(f(x,y)\) that is continuous on a region \(D\) of Type II, we have
\[\iint\limits_D f(x,y)\,dA = \iint\limits_D f(x,y)\,dx \space dy = \int_c^d \left[\int_{h_1(y)}^{h_2(y)} f(x,y)\,dx \right] dy. \nonumber \]
The integral in each of these expressions is an iterated integral, similar to those we have seen before. Notice that, in the inner integral in the first expression, we integrate \(f(x,y)\) with \(x\) being held constant and the limits of integration being \(g_1(x)\) and \(g_2(x)\). In the inner integral in the second expression, we integrate \(f(x,y)\) with \(y\) being held constant and the limits of integration are \(h_1(x)\) and \(h_2(x)\).
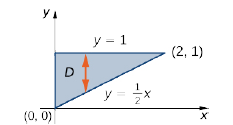
Example \(\PageIndex{2}\): Evaluating an Iterated Integral over a Type I Region
Evaluate the integral \(\displaystyle \iint \limits _D x^2 e^{xy} \,dA\) where \(D\) is shown in Figure \(\PageIndex{5}\).
Solution
First construct the region as a Type I region (Figure \(\PageIndex{5}\)). Here \(D = \big\{(x,y) \,|\, 0 \leq x \leq 2, \space \frac{1}{2} x \leq y \leq 1\big\}\). Then we have
\[\iint \limits _D x^2e^{xy} \,dA = \int_{x=0}^{x=2} \int_{y=1/2x}^{y=1} x^2e^{xy}\,dy\,dx. \nonumber \]
Therefore, we have
\[\begin{align*} \int_{x=0}^{x=2}\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\,dx &= \int_{x=0}^{x=2}\left[\int_{y=\frac{1}{2}x}^{y=1}x^2e^{xy}\,dy\right] dx & &\text{Iterated integral for a Type I region.}\\[5pt] &=\int_{x=0}^{x=2} \left.\left[ x^2 \frac{e^{xy}}{x} \right] \right|_{y=1/2x}^{y=1}\,dx & & \text{Integrate with respect to $y$}\\[5pt] &= \int_{x=0}^{x=2} \left[xe^x - xe^{x^2/2}\right]dx & & \text{Integrate with respect to $x$} \\[5pt] &=\left[xe^x - e^x - e^{\frac{1}{2}x^2} \right] \Big|_{x=0}^{x=2} = 2. \end{align*}\]
In Example \(\PageIndex{2}\), we could have looked at the region in another way, such as \(D = \big\{(x,y)\,|\,0 \leq y \leq 1, \space 0 \leq x \leq 2y\big\}\) (Figure \(\PageIndex{6}\)).
This is a Type II region and the integral would then look like
\[\iint \limits _D x^2e^{xy}\,dA = \int_{y=0}^{y=1} \int_{x=0}^{x=2y} x^2 e^{xy}\,dx \space dy. \nonumber \]
However, if we integrate first with respect to \(x\) this integral is lengthy to compute because we have to use integration by parts twice.
Example \(\PageIndex{3}\): Evaluating an Iterated Integral over a Type II Region
Evaluate the integral
\[\iint \limits _D (3x^2 + y^2) \,dA \nonumber \]
where \(D = \big\{(x,y)\,| \, -2 \leq y \leq 3, \space y^2 - 3 \leq x \leq y + 3\big\}\).
Solution
Notice that \(D\) can be seen as either a Type I or a Type II region, as shown in Figure \(\PageIndex{7}\). However, in this case describing \(D\) as Type I is more complicated than describing it as Type II. Therefore, we use \(D\) as a Type II region for the integration.
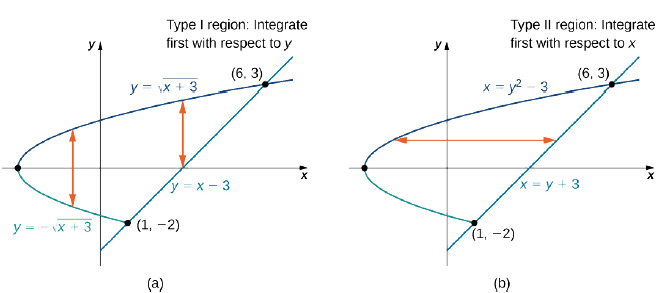
Choosing this order of integration, we have
\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[5pt] &=\int_{y=-2}^{y=3} \left. (x^3 + xy^2) \right|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[5pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\ &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[5pt] &= \left[ 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right]_{-2}^3 \\ &=\frac{2375}{7}. \end{align*}\]
Exercise \(\PageIndex{2}\)
Sketch the region \(D\) and evaluate the iterated integral \[\iint \limits _D xy \space dy \space dx \nonumber \] where \(D\) is the region bounded by the curves \(y = \cos \space x\) and \(y = \sin \space x\) in the interval \([-3\pi/4, \space \pi/4]\).
- Hint
-
Express \(D\) as a Type I region, and integrate with respect to \(y\) first.
- Answer
-
\(\frac{\pi}{4}\)
Recall from Double Integrals over Rectangular Regions the properties of double integrals. As we have seen from the examples here, all these properties are also valid for a function defined on a non-rectangular bounded region on a plane. In particular, property 3 states:
If \(R = S \cup T\) and \(S \cap T = 0\) except at their boundaries, then
\[\iint \limits _R f(x,y)\,dA = \iint\limits _S f(x,y)\,dA + \iint\limits _T f(x,y) \,dA. \nonumber \]
Similarly, we have the following property of double integrals over a non-rectangular bounded region on a plane.
Theorem: Decomposing Regions into Smaller Regions
Suppose the region \(D\) can be expressed as \(D = D_1 \cup D_2\) where \(D_1\) and \(D_2\) do not overlap except at their boundaries. Then
\[\iint \limits _D f(x,y) \,dA = \iint \limits _{D_1} f(x,y) \,dA + \iint \limits _{D_2} f(x,y) \,dA. \nonumber \]
This theorem is particularly useful for non-rectangular regions because it allows us to split a region into a union of regions of Type I and Type II. Then we can compute the double integral on each piece in a convenient way, as in the next example.
Example \(\PageIndex{4}\): Decomposing Regions
Express the region \(D\) shown in Figure \(\PageIndex{8}\) as a union of regions of Type I or Type II, and evaluate the integral
\[\iint \limits _D (2x + 5y)\,dA. \nonumber \]
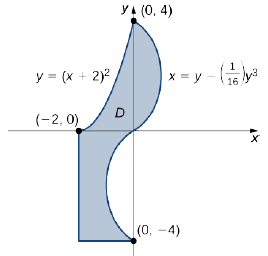
Solution
The region \(D\) is not easy to decompose into any one type; it is actually a combination of different types. So we can write it as a union of three regions \(D_1\), \(D_2\), and \(D_3\) where, \(D_1 = \big\{(x,y)\,| \, -2 \leq x \leq 0, \space 0 \leq y \leq (x + 2)^2 \big\}\), \(D_2 = \big\{(x,y)\,| \, 0 \leq y \leq 4, \space 0 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\), and \(D_3 = \big\{(x,y)\,| \, -4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16} y^3 \big) \big\}\). These regions are illustrated more clearly in Figure \(\PageIndex{9}\).
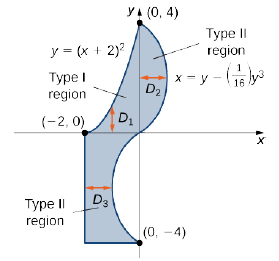
Here \(D_1\) is Type I and \(D_2\) and \(D_3\) are both of Type II. Hence,
\[\begin{align*} \iint\limits_D (2x + 5y)\,dA &= \iint\limits_{D_1} (2x + 5y)\,dA + \iint\limits_{D_2} (2x + 5y)\,dA + \iint\limits_{D_3} (2x + 5y)\,dA \\ &= \int_{x=-2}^{x=0} \int_{y=0}^{y=(x+2)^2} (2x + 5y) \,dy \space dx + \int_{y=0}^{y=4} \int_{x=0}^{x=y-(1/16)y^3} (2 + 5y)\,dx \space dy + \int_{y=-4}^{y=0} \int_{x=-2}^{x=y-(1/16)y^3} (2x + 5y)\,dx \space dy \\ &= \int_{x=-2}^{x=0} \left[\frac{1}{2}(2 + x)^2 (20 + 24x + 5x^2)\right]\,dx + \int_{y=0}^{y=4} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 \right]\,dy +\int_{y=-4}^{y=0} \left[\frac{1}{256}y^6 - \frac{7}{16}y^4 + 6y^2 + 10y - 4\right] \,dy\\ &= \frac{40}{3} + \frac{1664}{35} - \frac{1696}{35} = \frac{1304}{105}.\end{align*}\]
Now we could redo this example using a union of two Type II regions (see the Checkpoint).
Exercise \(\PageIndex{3}\)
Consider the region bounded by the curves \(y = \ln x\) and \(y = e^x\) in the interval \([1,2]\). Decompose the region into smaller regions of Type II.
- Hint
-
Sketch the region, and split it into three regions to set it up.
- Answer
-
\[\big\{(x,y)\,| \, 0 \leq y \leq 1, \space 1 \leq x \leq e^y \big\} \cup \big\{(x,y)\,| \, 1 \leq y \leq e, \space 1 \leq x \leq 2 \big\} \cup \big\{(x,y)\,| \, e \leq y \leq e^2, \space \ln y \leq x \leq 2 \big\} \nonumber \]
Exercise \(\PageIndex{4}\)
Redo Example \(\PageIndex{4}\) using a union of two Type II regions.
- Hint
-
\[\big\{(x,y)\,| \, 0 \leq y \leq 4, \space 2 + \sqrt{y} \leq x \leq \big(y - \frac{1}{16}y^3\big) \big\} \cup \big\{(x,y)\,| \, - 4 \leq y \leq 0, \space -2 \leq x \leq \big(y - \frac{1}{16}y^{13}\big) \big\} \nonumber \]
- Answer
-
Same as in the example shown.
Changing the Order of Integration
As we have already seen when we evaluate an iterated integral, sometimes one order of integration leads to a computation that is significantly simpler than the other order of integration. Sometimes the order of integration does not matter, but it is important to learn to recognize when a change in order will simplify our work.
Example \(\PageIndex{5}\): Changing the Order of Integration
Reverse the order of integration in the iterated integral
\[\int_{x=0}^{x=\sqrt{2}} \int_{y=0}^{y=2-x^2} xe^{x^2} \,dy \space dx. \nonumber \]
Then evaluate the new iterated integral.
Solution
The region as presented is of Type I. To reverse the order of integration, we must first express the region as Type II. Refer to Figure \(\PageIndex{10}\).

We can see from the limits of integration that the region is bounded above by \(y = 2 - x^2\) and below by \(y = 0\) where \(x\) is in the interval \([0, \sqrt{2}]\). By reversing the order, we have the region bounded on the left by \(x = 0\) and on the right by \(x = \sqrt{2 - y}\) where \(y\) is in the interval \([0, 2]\). We solved \(y = 2 - x^2\) in terms of \(x\) to obtain \(x = \sqrt{2 - y}\).
Hence
\[\begin{align*} \int_0^{\sqrt{2}} \int_0^{2-x^2} xe^{x^2} dy \space dx &= \int_0^2 \int_0^{\sqrt{2-y}} xe^{x^2}\,dx \space dy &\text{Reverse the order of integration then use substitution.} \\[4pt] &= \int_0^2 \left[\left.\frac{1}{2}e^{x^2}\right|_0^{\sqrt{2-y}}\right] dy = \int_0^2\frac{1}{2}(e^{2-y} - 1)\,dy \\[4pt] &= -\left.\frac{1}{2}(e^{2-y} + y)\right|_0^2 = \frac{1}{2}(e^2 - 3). \end{align*}\]
Example \(\PageIndex{6}\): Evaluating an Iterated Integral by Reversing the Order of Integration
Consider the iterated integral
\[\iint\limits_R f(x,y)\,dx \space dy \nonumber \]
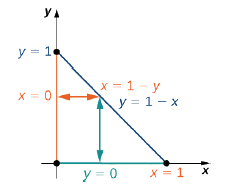
where \(z = f(x,y) = x - 2y\) over a triangular region \(R\) that has sides on \(x = 0, \space y = 0\), and the line \(x + y = 1\). Sketch the region, and then evaluate the iterated integral by
- integrating first with respect to \(y\) and then
- integrating first with respect to \(x\).
Solution
A sketch of the region appears in Figure \(\PageIndex{11}\).
We can complete this integration in two different ways.
a. One way to look at it is by first integrating \(y\) from \(y = 0\) to \(y = 1 - x\) vertically and then integrating \(x\) from \(x = 0\) to \(x = 1\):
\[\begin{align*} \iint\limits_R f(x,y) \,dx \space dy &= \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} (x - 2y) \,dy \space dx = \int_{x=0}^{x=1}\left(xy - 2y^2\right)\Big|_{y=0}^{y=1-x} dx \\[4pt] &=\int_{x=0}^{x=1} \left[ x(1 - x) - (1 - x)^2\right] \,dx = \int_{x=0}^{x=1} [ -1 + 3x - 2x^2] dx = \left[ -x + \frac{3}{2}x^2 - \frac{2}{3} x^3 \right]\Big|_{x=0}^{x=1} = -\frac{1}{6}. \end{align*}\]
b. The other way to do this problem is by first integrating \(x\) from \(x = 0\) to \(x = 1 - y\) horizontally and then integrating \(y\) from \(y = 0\) to \(y = 1\):
\[\begin{align*} \iint \limits _D (3x^2 + y^2)\,dA &= \int_{y=-2}^{y=3} \int_{x=y^2-3}^{x=y+3} (3x^2 + y^2) \,dx \space dy \\[4pt] &=\int_{y=-2}^{y=3} (x^3 + xy^2) \Big|_{y^2-3}^{y+3} \,dy & & \text{Iterated integral, Type II region}\\[4pt] &=\int_{y=-2}^{y=3} \left((y + 3)^3 + (y + 3)y^2 - (y^2 - 3)y^2\right)\,dy \\[4pt] &=\int_{-2}^3 (54 + 27y - 12y^2 + 2y^3 + 8y^4 - y^6)\,dy & & \text{Integrate with respect to $x$.} \\[4pt] &= \left( 54y + \frac{27y^2}{2} - 4y^3 + \frac{y^4}{2} + \frac{8y^5}{5} - \frac{y^7}{7} \right)\Big|_{-2}^3 \\[4pt] &=\frac{2375}{7}. \end{align*}\]
Exercise \(\PageIndex{5}\)
Evaluate the iterated integral \(\displaystyle \iint\limits_D (x^2 + y^2)\,dA\) over the region \(D\) in the first quadrant between the functions \(y = 2x\) and \(y = x^2\). Evaluate the iterated integral by integrating first with respect to \(y\) and then integrating first with resect to \(x\).
- Hint
-
Sketch the region and follow Example \(\PageIndex{6}\).
- Answer
-
\(\frac{216}{35}\)
Calculating Volumes, Areas, and Average Values
We can use double integrals over general regions to compute volumes, areas, and average values. The methods are the same as those in Double Integrals over Rectangular Regions, but without the restriction to a rectangular region, we can now solve a wider variety of problems.
Example \(\PageIndex{7}\): Finding the Volume of a Tetrahedron
Find the volume of the solid bounded by the planes \(x = 0, \space y = 0, \space z = 0\), and \(2x + 3y + z = 6\).
Solution
The solid is a tetrahedron with the base on the \(xy\)-plane and a height \(z = 6 - 2x - 3y\). The base is the region \(D\) bounded by the lines, \(x = 0\), \(y = 0\) and \(2x + 3y = 6\) where \(z = 0\) (Figure \(\PageIndex{12}\)). Note that we can consider the region \(D\) as Type I or as Type II, and we can integrate in both ways.
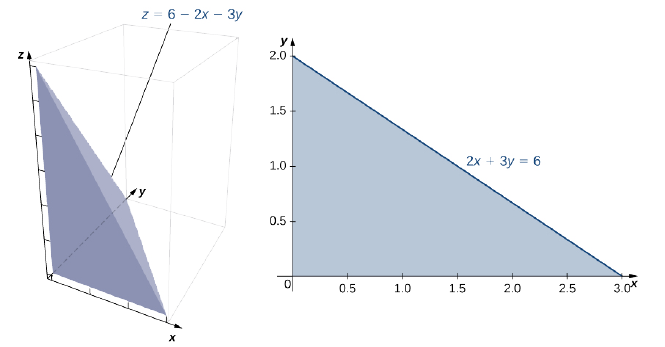
First, consider \(D\) as a Type I region, and hence \(D = \big\{(x,y)\,| \, 0 \leq x \leq 3, \space 0 \leq y \leq 2 - \frac{2}{3} x \big\}\).
Therefore, the volume is
\[\begin{align*} V &= \int_{x=0}^{x=3} \int_{y=0}^{y=2-(2x/3)} (6 - 2x - 3y) \,dy \space dx = \int_{x=0}^{x=3} \left[ \left.\left( 6y - 2xy - \frac{3}{2}y^2\right)\right|_{y=0}^{y=2-(2x/3)} \right] \,dx\\[4pt] &= \int_{x=0}^{x=3} \left[\frac{2}{3} (x - 3)^2 \right] \,dx = 6. \end{align*}\]
Now consider \(D\) as a Type II region, so \(D = \big\{(x,y)\,| \, 0 \leq y \leq 2, \space 0 \leq x \leq 3 - \frac{3}{2}y \big\}\). In this calculation, the volume is
\[\begin{align*} V &= \int_{y=0}^{y=2} \int_{x=0}^{x=3-(3y/2)} (6 - 2x - 3y)\,dx \space dy = \int_{y=0}^{y=2} \left[(6x - x^2 - 3xy)\Big|_{x=0}^{x=3-(3y/2)} \right] \,dy \\[4pt] &= \int_{y=0}^{y=2} \left[\frac{9}{4}(y - 2)^2 \right] \,dy = 6.\end{align*}\]
Therefore, the volume is 6 cubic units.
Exercise \(\PageIndex{6}\)
Find the volume of the solid bounded above by \(f(x,y) = 10 - 2x + y\) over the region enclosed by the curves \(y = 0\) and \(y = e^x\) where \(x\) is in the interval \([0,1]\).
- Hint
-
Sketch the region, and describe it as Type I.
- Answer
-
\(\frac{e^2}{4} + 10e - \frac{49}{4}\) cubic units
Finding the area of a rectangular region is easy, but finding the area of a non-rectangular region is not so easy. As we have seen, we can use double integrals to find a rectangular area. As a matter of fact, this comes in very handy for finding the area of a general non-rectangular region, as stated in the next definition.
Definition: Double Integrals
The area of a plane-bounded region \(D\) is defined as the double integral
\[\iint\limits_D 1\,dA. \nonumber \]
We have already seen how to find areas in terms of single integration. Here we are seeing another way of finding areas by using double integrals, which can be very useful, as we will see in the later sections of this chapter.
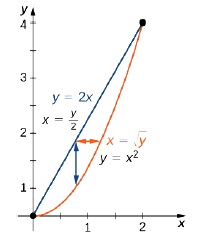
Example \(\PageIndex{8}\): Finding the Area of a Region
Find the area of the region bounded below by the curve \(y = x^2\) and above by the line \(y = 2x\) in the first quadrant (Figure \(\PageIndex{13}\)).
Solution
We just have to integrate the constant function \(f(x,y) = 1\) over the region. Thus, the area \(A\) of the bounded region is \(\displaystyle \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} dy \space dx \space \text{or} \space \int_{y=0}^{y=4} \int_{x=y/2}^{x=\sqrt{y}} dx \space dy:\)
\[\begin{align*} A &= \iint\limits_D 1\,dx \space dy \\[4pt] &= \int_{x=0}^{x=2} \int_{y=x^2}^{y=2x} 1\,dy \space dx \\[4pt] &= \int_{x=0}^{x=2} \left(y\Big|_{y=x^2}^{y=2x} \right) \,dx \\[4pt] &= \int_{x=0}^{x=2} (2x - x^2)\,dx \\[4pt] &= \left(x^2 - \frac{x^3}{3}\right) \Big|_0^2 = \frac{4}{3}. \end{align*}\]
Exercise \(\PageIndex{7}\)
Find the area of a region bounded above by the curve \(y = x^3\) and below by \(y = 0\) over the interval \([0,3]\).
- Hint
-
Sketch the region.
- Answer
-
\(\frac{81}{4}\) square units
We can also use a double integral to find the average value of a function over a general region. The definition is a direct extension of the earlier formula.
Definition: The Average Value of a Function
If \(f (x,y)\) is integrable over a plane-bounded region \(D\) with positive area \(A(D)\), then the average value of the function is
\[f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA. \nonumber \]
Note that the area is \(\displaystyle A(D) = \iint\limits_D 1\,dA\).
Example \(\PageIndex{9}\): Finding an Average Value
Find the average value of the function \(f(x,y) = 7xy^2\) on the region bounded by the line \(x = y\) and the curve \(x = \sqrt{y}\) (Figure \(\PageIndex{14}\)).
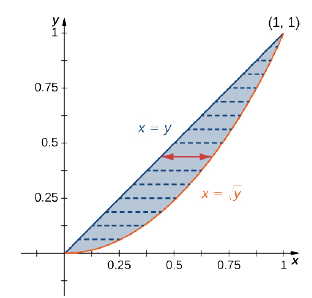
Solution
First find the area \(A(D)\) where the region \(D\) is given by the figure. We have
\[A(D) = \iint\limits_D 1\,dA = \int_{y=0}^{y=1} \int_{x=y}^{x=\sqrt{y}} 1\,dx \space dy = \int_{y=0}^{y=1} \left[x \Big|_{x=y}^{x=\sqrt{y}} \right] \,dy = \int_{y=0}^{y=1} (\sqrt{y} - y) \,dy = \frac{2}{3}\left. y^{2/3} - \frac{y^2}{2} \right|_0^1 = \frac{1}{6} \nonumber \]
Then the average value of the given function over this region is
\[\begin{align*} f_{ave} = \frac{1}{A(D)} \iint\limits_D f(x,y) \,dA = \frac{1}{A(D)} \int_{y=0}^{y=1}\int_{x=y}^{x=\sqrt{y}} 7xy^2 \,dx \space dy = \frac{1}{1/6} \int_{y=0}^{y=1} \left[ \left. \frac{7}{2} x^2y^2 \right|_{x=y}^{x=\sqrt{y}} \right] \,dy \\ = 6 \int_{y=0}^{y=1} \left[ \frac{7}{2} y^2 (y - y^2)\right] \,dy = 6\int_{y=0}^{y=1} \left[ \frac{7}{2} (y^3 -y^4) \right] \,dy = \frac{42}{2} \left. \left( \frac{y^4}{4} - \frac{y^5}{5}\right) \right|_0^1 = \frac{42}{40} = \frac{21}{20}. \end{align*}\]
Exercise \(\PageIndex{8}\)
Find the average value of the function \(f(x,y) = xy\) over the triangle with vertices \((0,0), \space (1,0)\) and \((1,3)\).
- Hint
-
Express the line joining \((0,0)\) and \((1,3)\) as a function \(y = g(x)\).
- Answer
-
\(\frac{3}{4}\)
Improper Double Integrals
An improper double integral is an integral \(\displaystyle \iint\limits_D f \,dA\) where either \(D\) is an unbounded region or \(f\) is an unbounded function. For example, \(D = \big\{(x,y) \,|\,|x - y| \geq 2\big\}\) is an unbounded region, and the function \(f(x,y) = 1/(1 - x^2 - 2y^2)\) over the ellipse \(x^2 + 3y^2 \geq 1\) is an unbounded function. Hence, both of the following integrals are improper integrals:
- \[\iint\limits_D xy \space dA \space \text{where} \space D = \big\{(x,y)| | \, x - y| \geq 2 \big\}; \nonumber \]
- \[\iint\limits_D \frac{1}{1 - x^2 -2y^2}\,dA \space \text{where} \space D = \big\{(x,y)| \, x^2 + 3y^2 \leq 1 \big\}. \nonumber \]
In this section we would like to deal with improper integrals of functions over rectangles or simple regions such that f has only finitely many discontinuities. Not all such improper integrals can be evaluated; however, a form of Fubini’s theorem does apply for some types of improper integrals.
Theorem: Fubini’s Theorem for Improper Integrals
If \(D\) is a bounded rectangle or simple region in the plane defined by
\(\big\{(x,y)\,: a \leq x \leq b, \space g(x) \leq y \leq h(x) \big\}\) and also by
\(\big\{(x,y)\,: c \leq y \leq d, \space j(y) \leq x \leq k(y)\big\}\) and \(f\) is a nonnegative function on \(D\) with finitely many discontinuities in the interior of \(D\) then
\[\iint\limits_D f \space dA = \int_{x=a}^{x=b} \int_{y=g(x)}^{y=h(x)} f(x,y) \,dy \space dx = \int_{y=c}^{y=d} \int_{x=j(y)}^{x=k(y)} f(x,y) \,dx \space dy \nonumber \]
It is very important to note that we required that the function be nonnegative on \(D\) for the theorem to work. We consider only the case where the function has finitely many discontinuities inside \(D\).
Example \(\PageIndex{10}\): Evaluating a Double Improper Integral
Consider the function \(f(x,y) = \frac{e^y}{y}\) over the region \(D = \big\{(x,y)\,: 0 \leq x \leq 1, \space x \leq y \leq \sqrt{x}\big\}.\)
Notice that the function is nonnegative and continuous at all points on \(D\) except \((0,0)\). Use Fubini’s theorem to evaluate the improper integral.
Solution
First we plot the region \(D\) (Figure \(\PageIndex{15}\)); then we express it in another way.
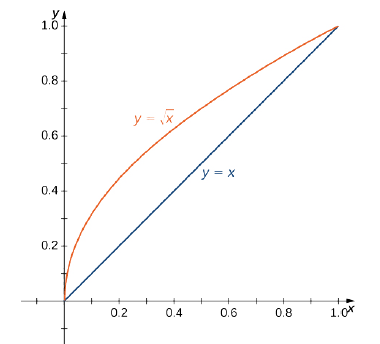
The other way to express the same region \(D\) is
\[D = \big\{(x,y)\,: \, 0 \leq y \leq 1, \space y^2 \leq x \leq y \big\}. \nonumber \]
Thus we can use Fubini’s theorem for improper integrals and evaluate the integral as
\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy. \nonumber \]
Therefore, we have
\[\int_{y=0}^{y=1} \int_{x=y^2}^{x=y} \frac{e^y}{y} \,dx \space dy = \int_{y=0}^{y=1} \left. \frac{e^y}{y}x\right|_{x=y^2}^{x=y} \,dy = \int_{y=0}^{y=1} \frac{e^y}{y} (y - y^2) \,dy = \int_0^1 (e^y - ye^y)\,dy = e - 2. \nonumber \]
As mentioned before, we also have an improper integral if the region of integration is unbounded. Suppose now that the function \(f\) is continuous in an unbounded rectangle \(R\).
Theorem: Improper Integrals on an Unbounded Region
If \(R\) is an unbounded rectangle such as \(R = \big\{(x,y)\,: \, a \leq x \leq \infty, \space c \leq y \leq \infty \big\}\), then when the limit exists, we have
\[\iint\limits_R f(x,y) \,dA = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_a^b \left(\int_c^d f (x,y) \,dy \right) dx = \lim_{(b,d) \rightarrow (\infty, \infty)} \int_c^d \left(\int_a^b f(x,y) \,dx \right) dy. \nonumber \]
The following example shows how this theorem can be used in certain cases of improper integrals.
Example \(\PageIndex{11}\)
Evaluate the integral \(\iint\limits_R xye^{-x^2-y^2}\,dA\) where \(R\) is the first quadrant of the plane.
Solution
The region \(R\) is the first quadrant of the plane, which is unbounded. So
\[\begin{align*} \iint\limits_R xye^{-x^2-y^2} \,dA &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{x=0}^{x=b} \left(\int_{y=0}^{y=d} xye^{-x^2-y^2} dy\right) \,dx \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \int_{y=0}^{x=b} xye^{-x^2-y^2} \,dy \\ &= \lim_{(b,d) \rightarrow (\infty, \infty)} \frac{1}{4} \left(1 - e^{-b^2}\right) \left( 1 - e^{-d^2}\right) = \frac{1}{4} \end{align*}\]
Thus,
\[\iint\limits_R xye^{-x^2-y^2}\,dA \nonumber \]
is convergent and the value is \(\frac{1}{4}\).
Exercise \(\PageIndex{9}\)
\[\iint\limits_D \frac{y}{\sqrt{1 - x^2 - y^2}}dA \nonumber \] where \(D = \big\{(x,y)\,: \, x \geq 0, \space y \geq 0, \space x^2 + y^2 \leq 1 \big\}\).
- Hint
-
Notice that the integral is nonnegative and discontinuous on \(x^2 + y^2 = 1\). Express the region \(D\) as \(D = \big\{(x,y)\,: \, 0 \leq x \leq 1, \space 0 \leq y \leq \sqrt{1 - x^2} \big\}\) and integrate using the method of substitution.
- Answer
-
\(\frac{\pi}{4}\)
In some situations in probability theory, we can gain insight into a problem when we are able to use double integrals over general regions. Before we go over an example with a double integral, we need to set a few definitions and become familiar with some important properties.
Definition: Joint Density Function
Consider a pair of continuous random variables \(X\) and \(Y\) such as the birthdays of two people or the number of sunny and rainy days in a month. The joint density function \(f\) of \(X\) and \(Y\) satisfies the probability that \((X,Y)\) lies in a certain region \(D\):
\[P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA. \nonumber \]
Since the probabilities can never be negative and must lie between 0 and 1 the joint density function satisfies the following inequality and equation:
\[f(x,y) \geq 0 \space \text{and} \space \iint\limits_R f(x,y) \,dA = 1. \nonumber \]
Definition: Independent Random Variables
The variables \(X\) and \(Y\) are said to be independent random variables if their joint density function is the product of their individual density functions:
\[f(x,y) = f_1(x) f_2(y). \nonumber \]
Example \(\PageIndex{12}\): Application to Probability
At Sydney’s Restaurant, customers must wait an average of 15 minutes for a table. From the time they are seated until they have finished their meal requires an additional 40 minutes, on average. What is the probability that a customer spends less than an hour and a half at the diner, assuming that waiting for a table and completing the meal are independent events?
Solution
Waiting times are mathematically modeled by exponential density functions, with \(m\) being the average waiting time, as
\[f(t) = \begin{cases} 0, & \text{if}\; t<0 \\ \dfrac{1}{m}e^{-t/m}, & \text{if} \; t\geq 0.\end{cases} \nonumber \]
if \(X\) and \(Y\) are random variables for ‘waiting for a table’ and ‘completing the meal,’ then the probability density functions are, respectively,
\[f_1(x) = \begin{cases} 0, & \text{if}\; x<0. \\ \dfrac{1}{15} e^{-x/15}, & \text{if} \; x\geq 0. \end{cases} \quad \text{and} \quad f_2(y) = \begin{cases} 0, & \text{if}\; y<0 \\ \dfrac{1}{40} e^{-y/40}, & \text{if}\; y\geq 0. \end{cases} \nonumber \]
Clearly, the events are independent and hence the joint density function is the product of the individual functions
\[f(x,y) = f_1(x)f_2(y) = \begin{cases} 0, & \text{if} \; x<0 \; \text{or} \; y<0, \\ \dfrac{1}{600} e^{-x/15}, & \text{if} \; x,y\geq 0 \end{cases} \nonumber \]
We want to find the probability that the combined time \(X + Y\) is less than 90 minutes. In terms of geometry, it means that the region \(D\) is in the first quadrant bounded by the line \(x + y = 90\) (Figure \(\PageIndex{16}\)).
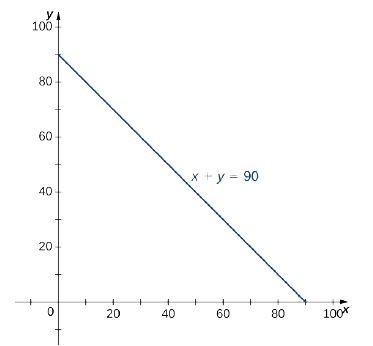
Hence, the probability that \((X,Y)\) is in the region \(D\) is
\[P(X + Y \leq 90) = P((X,Y) \in D) = \iint\limits_D f(x,y) \,dA = \iint\limits_D \frac{1}{600}e^{-x/15} e^{-y/40} \,dA. \nonumber \]
Since \(x + y = 90\) is the same as \(y = 90 - x\), we have a region of Type I, so
\[\begin{align*} D &= \big\{(x,y)\,|\,0 \leq x \leq 90, \space 0 \leq y \leq 90 - x\big\}, \\[6pt] P(X + Y \leq 90) &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(/15}e^{-y/40}dx \space dy = \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x}e^{-x/15}e^{-y/40} dx \space dy \\[6pt] &= \frac{1}{600} \int_{x=0}^{x=90} \int_{y=0}^{y=90-x} e^{-(x/15+y/40)}dx \space dy = 0.8328 \end{align*}\]
Thus, there is an \(83.2\%\) chance that a customer spends less than an hour and a half at the restaurant.
Another important application in probability that can involve improper double integrals is the calculation of expected values. First we define this concept and then show an example of a calculation.
Definition: Expected Values
In probability theory, we denote the expected values \(E(X)\) and \(E(Y)\) respectively, as the most likely outcomes of the events. The expected values \(E(X)\) and \(E(Y)\) are given by
\[E(X) = \iint\limits_S x\,f(x,y) \,dA \space and \space E(Y) = \iint\limits_S y\,f (x,y) \,dA, \nonumber \]
where \(S\) is the sample space of the random variables \(X\) and \(Y\).
Example \(\PageIndex{13}\): Finding Expected Value
Find the expected time for the events ‘waiting for a table’ and ‘completing the meal’ in Example \(\PageIndex{12}\).
Solution
Using the first quadrant of the rectangular coordinate plane as the sample space, we have improper integrals for \(E(X)\) and \(E(Y)\). The expected time for a table is
\[\begin{align*} E(X) &= \iint\limits_S x\frac{1}{600} e^{-x/15}e^{-y/40} \, dA\\[6pt]
&= \frac{1}{600} \int_{x=0}^{x=\infty} \int_{y=0}^{y=\infty} xe^{-x/15} e^{-y/40}dA\\[6pt]
&= \frac{1}{600} \lim_{(a,b) \rightarrow (\infty, \infty)} \int_{x=0}^{x=a} \int_{y=0}^{y=b} xe^{-x/15} e^{-y/40} dx \space dy \\[6pt]
&= \frac{1}{600} \left(\lim_{a\rightarrow \infty}\int_{x=0}^{x=a} xe^{-x/15} dx \right) \left( \lim_{b\rightarrow \infty} \int_{y=0}^{y=b} e^{-y/40} dy \right) \\[6pt]
&= \frac{1}{600}\left(\left. (\lim_{a\rightarrow \infty} (-15e^{-x/15}(x + 15)))\right|_{x=0}^{x=a} \right) \left( \left. ( \lim_{b\rightarrow \infty}(-40e^{-y/40})) \right|_{y=0}^{y=b}\right) \\[6pt]
&=\frac{1}{600} \left( \lim_{a \rightarrow \infty} (-15e^{-a/15} (x + 15) + 225) \right)\left(\lim_{b\rightarrow \infty} (-40e^{-b/40} + 40) \right) \\[6pt]
&= \frac{1}{600} (225)(40) = 15. \end{align*}\]
A similar calculation shows that \(E(Y) = 40\). This means that the expected values of the two random events are the average waiting time and the average dining time, respectively.
Exercise \(\PageIndex{10}\)
The joint density function for two random variables \(X\) and \(Y\) is given by
\[f(x,y) =\begin{cases}\frac{1}{600} (x^2 + y^2),\; & \text{if} \; \leq x \leq 15, \; 0 \leq y \leq 10 \\ 0, & \text{otherwise} \end{cases} \nonumber \]
Find the probability that \(X\) is at most 10 and \(Y\) is at least 5.
- Hint
-
Compute the probability
\[P(X \leq 10, \space Y \geq 5) = \int_{x=-\infty}^{10} \int_{y=5}^{y=10} \frac{1}{6000} (x^2 + y^2) dy \space dx. \nonumber \]
- Answer
-
\(\frac{55}{72} \approx 0.7638\)
Key Concepts
- A general bounded region \(D\) on the plane is a region that can be enclosed inside a rectangular region. We can use this idea to define a double integral over a general bounded region.
- To evaluate an iterated integral of a function over a general nonrectangular region, we sketch the region and express it as a Type I or as a Type II region or as a union of several Type I or Type II regions that overlap only on their boundaries.
- We can use double integrals to find volumes, areas, and average values of a function over general regions, similarly to calculations over rectangular regions.
- We can use Fubini’s theorem for improper integrals to evaluate some types of improper integrals.
Key Equations
- Iterated integral over a Type I region
\[\iint\limits_D f(x,y) \,dA = \iint\limits_D f(x,y) \,dy \space dx = \int_a^b \left[\int_{g_1(x)}^{g_2(x)} f(x,y) \,dy \right] dx \nonumber \]
- Iterated integral over a Type II region
\[\iint\limits_D f(x,y) \,dA = \iint\limits_D (x,y) \,dx \space dy = \int_c^d \left[ \int_{h_1(y)}^{h_2(y)} f(x,y) \,dx \right] dy \nonumber \]
Glossary
- improper double integral
- a double integral over an unbounded region or of an unbounded function
- Type I
- a region \(D\) in the \(xy\)- plane is Type I if it lies between two vertical lines and the graphs of two continuous functions \(g_1(x)\) and \(g_2(x)\)
- Type II
- a region \(D\) in the \(xy\)-plane is Type II if it lies between two horizontal lines and the graphs of two continuous functions \(h_1(y)\) and \(h_2(h)\)

