14.3E: Double Integrals in Polar Coordinates (Exercises)

Terms and Concepts

1. When evaluating $\displaystyle \int\int_R f(x,y)\,dA$ using polar coordinates, $f(x,y)$ is replaced with _______ and $dA$ is replaced with _______.

Answer

$f(x,y)$ is replaced with $f(r\cos \theta, r\sin\theta)$ and $dA$ is replaced with $r\,dr\,d\theta$.

2. Why would one be interested in evaluating a double integral with polar coordinates?

Defining Polar Regions

In exercises 3 - 6, express the region $R$ in polar coordinates.

3) $R$ is the region of the disk of radius 2 centered at the origin that lies in the first quadrant.

Answer

$R = \big\{(r, \theta)\,|\,0 \leq r \leq 2, \space 0 \leq \theta \leq \frac{\pi}{2}\big\}$

4) $R$ is the region of the disk of radius 3 centered at the origin.

5) $R$ is the region between the circles of radius 4 and radius 5 centered at the origin that lies in the second quadrant.

Answer

$R = \big\{(r, \theta)\,|\,4 \leq r \leq 5, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}$

6) $R$ is the region bounded by the $y$-axis and $x = \sqrt{1 - y^2}$.

7) $R$ is the region bounded by the $x$-axis and $y = \sqrt{2 - x^2}$.

Answer

$R = \big\{(r, \theta)\,|\,0 \leq r \leq \sqrt{2}, \space 0 \leq \theta \leq \pi\big\}$

8) $R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4x\big\}$

9) $R = \big\{(x,y)\,|\,x^2 + y^2 \leq 4y\big\}$

Answer

$R = \big\{(r, \theta)\,|\,0 \leq r \leq 4 \space \sin \theta, \space 0 \leq \theta \leq \pi\big\}$

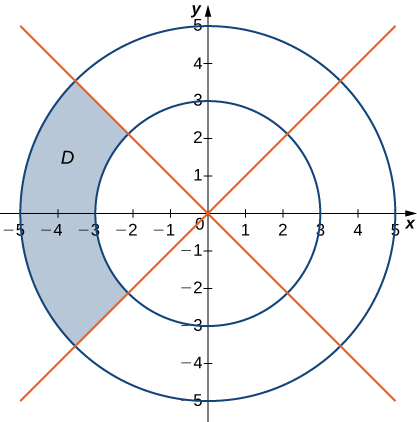
In exercises 10 - 15, the graph of the polar rectangular region $D$ is given. Express $D$ in polar coordinates.  In exercises 10 - 13 the regions are bounded by circles centered at the origin, the coordinate axes, and/or lines of the  form $y=\pm x$ (each of which should be able to be identified by inspection).

10)

11)

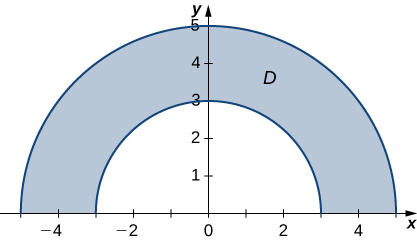
Answer

$D = \big\{(r, \theta)\,|\, 3 \leq r \leq 5, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{2}\big\}$

12)

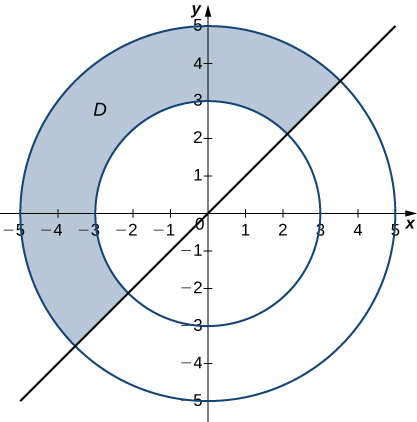
13)

Answer

$D = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space \frac{3\pi}{4} \leq \theta \leq \frac{5\pi}{4}\big\}$

14) In the following graph, the region $D$ is situated below $y = x$ and is bounded by $x = 1, \space x = 5$, and $y = 0$.

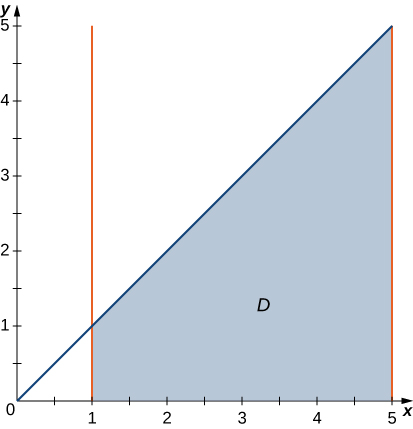
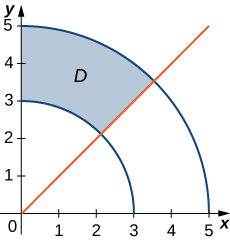
15) In the following graph, the region $D$ is bounded by $y = x$ and $y = x^2$.

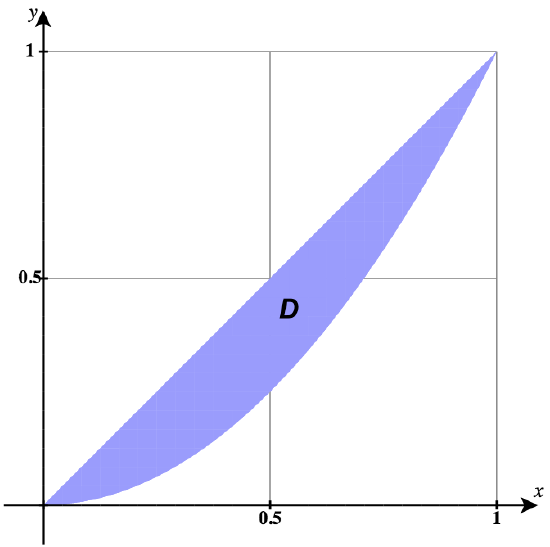
Answer

$D = \big\{(r, \theta)\,|\,0 \leq r \leq \tan \theta \space \sec \theta, \space 0 \leq \theta \leq \frac{\pi}{4}\big\}$

Evaluating Polar Double Integrals

In exercises 16 - 25, evaluate the double integral $\displaystyle \iint_R f(x,y) \,dA$ over the polar rectangular region $R$.

16) $f(x,y) = x^2 + y^2$, $R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}$

17) $f(x,y) = x + y$, $R = \big\{(r, \theta)\,|\,3 \leq r \leq 5, \space 0 \leq \theta \leq 2\pi\big\}$

Answer

$0$

18) $f(x,y) = x^2 + xy, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \pi \leq \theta \leq 2\pi\big\}$

19) $f(x,y) = x^4 + y^4, \space R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{3\pi}{2} \leq \theta \leq 2\pi\big\}$

Answer

$\frac{63\pi}{16}$

20) $f(x,y) = \sqrt[3]{x^2 + y^2}$, where $R = \big\{(r, \theta)\,|\,0 \leq r \leq 1, \space \frac{\pi}{2} \leq \theta \leq \pi\big\}$.

21) $f(x,y) = x^4 + 2x^2y^2 + y^4$, where $R = \big\{(r,\theta)\,|\,3 \leq r \leq 4, \space \frac{\pi}{3} \leq \theta \leq \frac{2\pi}{3}\big\}$.

Answer

$\frac{3367\pi}{18}$

22) $f(x,y) = \sin (\arctan \frac{y}{x})$, where $R = \big\{(r, \theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}$

23) $f(x,y) = \arctan \left(\frac{y}{x}\right)$, where $R = \big\{(r, \theta)\,|\,2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}$

Answer

$\frac{35\pi^2}{576}$

24) $\displaystyle \iint_R e^{x^2+y^2} \left[1 + 2 \space \arctan \left(\frac{y}{x}\right)\right] \,dA, \space R = \big\{(r,\theta)\,|\,1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \frac{\pi}{3}\big\}$

25) $\displaystyle \iint_R \left(e^{x^2+y^2} + x^4 + 2x^2y^2 + y^4 \right) \arctan \left(\frac{y}{x}\right) \,dA, \space R = \big\{(r, \theta )\,|\,1 \leq r \leq 2, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}$

Answer

$\frac{7}{576}\pi^2 (21 - e + e^4)$

Converting Double Integrals to Polar Form

In exercises 26 - 29, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.

26) $\displaystyle \int_1^2 \int_0^x (x^2 + y^2)\,dy \space dx = \int_0^{\frac{\pi}{4}} \int_{\sec \theta}^{2 \space \sec \theta}r^3 \,dr \space d\theta$

27) $\displaystyle \int_2^3 \int_0^x \frac{x}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \int_{2\sec\theta}^{3\sec \theta} \,r \space \cos \theta \space dr \space d\theta$

Answer

$\frac{5}{2} \ln (1 + \sqrt{2})$

28) $\displaystyle \int_0^1 \int_{x^2}^x \frac{1}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \space dr \space d\theta$

29) $\displaystyle \int_0^1 \int_{x^2}^x \frac{y}{\sqrt{x^2 + y^2}}\,dy \space dx = \int_0^{\pi/4} \displaystyle \int_0^{\tan \theta \space \sec \theta} \,r \space \sin \theta \space dr \space d\theta$

Answer

$\frac{1}{6}(2 - \sqrt{2})$

In exercises 30 - 37, draw the region of integration, $R$, labeling all limits of integration, convert the integrals to polar coordinates and evaluate them.

30) $\displaystyle \int_0^3 \int_0^{\sqrt{9-y^2}}\left(x^2 + y^2\right)\,dx \space dy$

31) $\displaystyle \int_0^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}}\left(x^2 + y^2\right)^2\,dx \space dy$

Answer

$\displaystyle \int_0^{\pi} \int_0^2 r^5 \,dr \space d\theta \quad = \quad \frac{32\pi}{3}$

32) $\displaystyle \int_0^1 \int_0^{\sqrt{1-x^2}} (x + y) \space dy \space dx$

33) $\displaystyle \int_0^4 \int_{-\sqrt{16-x^2}}^{\sqrt{16-x^2}} \sin (x^2 + y^2) \space dy \space dx$

Answer

$\displaystyle \int_{-\pi/2}^{\pi/2} \int_0^4 \,r \space \sin (r^2) \space dr \space d\theta \quad = \quad \pi \space \sin^2 8$

34) $\displaystyle \int_0^5 \int_{-\sqrt{25-x^2}}^{\sqrt{25-x^2}}\sqrt{x^2+y^2}\,dy\,dx$

35) $\displaystyle \int_{-4}^4 \int_{-\sqrt{16-y^2}}^{0}(2y-x)\,dx\,dy$

Answer

$\displaystyle \int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} \int_0^{4} \big( 2r\sin \theta - r\cos\theta\big) \,r\,dr \space d\theta \quad = \quad \frac{128}{3}$

36) $\displaystyle \int_0^2 \int_{y}^{\sqrt{8-y^2}}(x+y)\,dx\,dy$

37) $\displaystyle \int_{-2}^{-1} \int_{0}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_{-1}^1\int_{\sqrt{1-x^2}}^{\sqrt{4-x^2}}(x+5)\,dy\,dx+\int_1^2\int_0^{\sqrt{4-x^2}}(x+5)\,dy\,dx$

Answer

$\displaystyle \int_{0}^{\pi} \int_1^{2} \big( r\cos \theta + 5\big) \,r\,dr \space d\theta \quad = \quad \frac{15\pi}{2}$

38) Evaluate the integral $\displaystyle \iint_D r \,dA$ where $D$ is the region bounded by the polar axis and the upper half of the cardioid $r = 1 + \cos \theta$.

39) Find the area of the region $D$ bounded by the polar axis and the upper half of the cardioid $r = 1 + \cos \theta$.

Answer

$\frac{3\pi}{4}$

40) Evaluate the integral $\displaystyle \iint_D r \,dA,$ where $D$ is the region bounded by the part of the four-leaved rose $r = \sin 2\theta$ situated in the first quadrant (see the following figure).

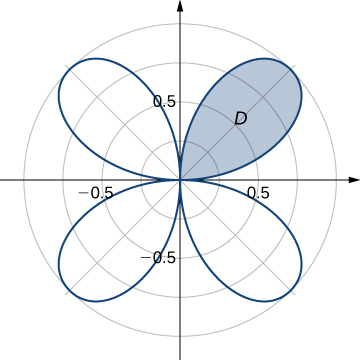
41) Find the total area of the region enclosed by the four-leaved rose $r = \sin 2\theta$ (see the figure in the previous exercise).

Answer

$\frac{\pi}{2}$

42) Find the area of the region $D$ which is the region bounded by $y = \sqrt{4 - x^2}$, $x = \sqrt{3}$, $x = 2$, and $y = 0$.

43) Find the area of the region $D$, which is the region inside the disk $x^2 + y^2 \leq 4$ and to the right of the line $x = 1$.

Answer

$\frac{1}{3}(4\pi - 3\sqrt{3})$

44) Determine the average value of the function $f(x,y) = x^2 + y^2$ over the region $D$ bounded by the polar curve $r = \cos 2\theta$, where $-\frac{\pi}{4} \leq \theta \leq \frac{\pi}{4}$ (see the following graph).

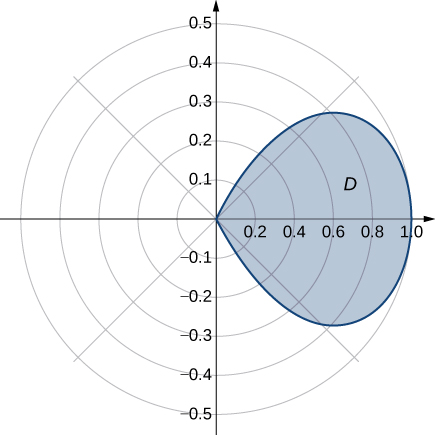
45) Determine the average value of the function $f(x,y) = \sqrt{x^2 + y^2}$ over the region $D$ bounded by the polar curve $r = 3\sin 2\theta$, where $0 \leq \theta \leq \frac{\pi}{2}$ (see the following graph).

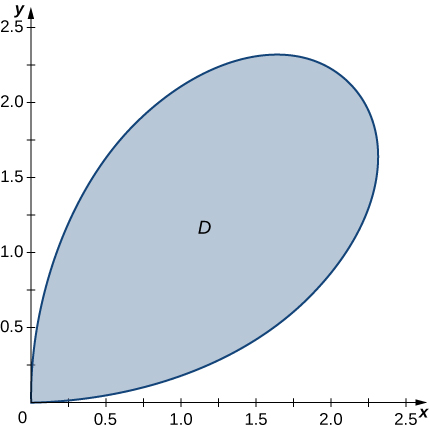
Answer

$\frac{16}{3\pi}$

46) Find the volume of the solid situated in the first octant and bounded by the paraboloid $z = 1 - 4x^2 - 4y^2$ and the planes $x = 0, \space y = 0$, and $z = 0$.

47) Find the volume of the solid bounded by the paraboloid $z = 2 - 9x^2 - 9y^2$ and the plane $z = 1$.

Answer

$\frac{\pi}{18}$

48)

1. Find the volume of the solid $S_1$ bounded by the cylinder $x^2 + y^2 = 1$ and the planes $z = 0$ and $z = 1$.
2. Find the volume of the solid $S_2$ outside the double cone $z^2 = x^2 + y^2$ inside the cylinder $x^2 + y^2 = 1$, and above the plane $z = 0$.
3. Find the volume of the solid inside the cone $z^2 = x^2 + y^2$ and below the plane $z = 1$ by subtracting the volumes of the solids $S_1$ and $S_2$.

49)

1. Find the volume of the solid $S_1$ inside the unit sphere $x^2 + y^2 + z^2 = 1$ and above the plane $z = 0$.
2. Find the volume of the solid $S_2$ inside the double cone $(z - 1)^2 = x^2 + y^2$ and above the plane $z = 0$.
3. Find the volume of the solid outside the double cone $(z - 1)^2 = x^2 + y^2$ and inside the sphere $x^2 + y^2 + z^2 = 1$.

Answer

a. $\frac{2\pi}{3}$; b. $\frac{\pi}{2}$; c. $\frac{\pi}{6}$

In Exercises 50-51, special double integrals are presented that are especially well suited for evaluation in polar coordinates.

50) The surface of a right circular cone with height $h$ and base radius $a$ can be described by the equation $f(x,y)=h-h\sqrt{\frac{x^2}{a^2}+\frac{y^2}{a^2}}$, where the tip of the cone lies at $(0,0,h)$ and the circular base lies in the $xy$-plane, centered at the origin.
Confirm that the volume of a right circular cone with height $h$ and base radius $a$ is $V=\frac{1}{3}\pi a^2h$ by evaluating $\displaystyle \int\int_R f(x,y)\,dA$ in polar coordinates.

51) Consider $\displaystyle \int\int_R e^{-(x^2+y^2)}\,dA.$
(a) Why is this integral difficult to evaluate in rectangular coordinates, regardless of the region $R$?
(b) Let $R$ be the region bounded by the circle of radius $a$ centered at the origin. Evaluate the double integral using polar coordinates.
(c) Take the limit of your answer from (b), as $a\to \infty$. What does this imply about the volume under the surface of $e^{-(x^2+y^2)}$ over the entire $xy$-plane?

For the following two exercises, consider a spherical ring, which is a sphere with a cylindrical hole cut so that the axis of the cylinder passes through the center of the sphere (see the following figure).

52) If the sphere has radius 4 and the cylinder has radius 2 find the volume of the spherical ring.

53) A cylindrical hole of diameter 6 cm is bored through a sphere of radius 5 cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.

Answer

$\frac{256\pi}{3} \space \text{cm}^3$

54) Find the volume of the solid that lies under the double cone $z^2 = 4x^2 + 4y^2$, inside the cylinder $x^2 + y^2 = x$, and above the plane $z = 0$.

55) Find the volume of the solid that lies under the paraboloid $z = x^2 + y^2$, inside the cylinder $x^2 + y^2 = 1$ and above the plane $z = 0$.

Answer

$\frac{3\pi}{32}$

56) Find the volume of the solid that lies under the plane $x + y + z = 10$ and above the disk $x^2 + y^2 = 4x$.

57) Find the volume of the solid that lies under the plane $2x + y + 2z = 8$ and above the unit disk $x^2 + y^2 = 1$.

Answer

$4\pi$

58) A radial function $f$ is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is, $f (x,y) = g(r)$, where $r = \sqrt{x^2 + y^2}$. Show that if $f$ is a continuous radial function, then

$$\iint_D f(x,y)dA = (\theta_2 - \theta_1) [G(R_2) - G(R_1)], \space where \space G'(r) = rg(r) \nonumber$$ and $(x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}$, with $0 \leq R_1 < R_2$ and $0 \leq \theta_1 < \theta_2 \leq 2\pi$.

59) Use the information from the preceding exercise to calculate the integral $\displaystyle \iint_D (x^2 + y^2)^3 dA,$ where $D$ is the unit disk.

Answer

$\frac{\pi}{4}$

60) Let $f(x,y) = \dfrac{F'(r)}{r}$ be a continuous radial function defined on the annular region $D = \big\{(r,\theta)\,|\,R_1 \leq r \leq R_2, \space 0 \leq \theta \leq 2\pi\big\}$, where $r = \sqrt{x^2 + y^2}$, $0 < R_1 < R_2$, and $F$ is a differentiable function.

Show that $\displaystyle \iint_D f(x,y)\,dA = 2\pi [F(R_2) - F(R_1)].$

61) Apply the preceding exercise to calculate the integral $\displaystyle \iint_D \frac{e^{\sqrt{x^2+y^2}}}{\sqrt{x^2 + y^2}} \,dx \space dy$ where $D$ is the annular region between the circles of radii 1 and 2 situated in the third quadrant.

Answer

$\frac{1}{2} \pi e(e - 1)$

62) Let $f$ be a continuous function that can be expressed in polar coordinates as a function of $\theta$ only; that is, $f(x,y) = h(\theta)$, where $(x,y) \in D = \big\{(r, \theta)\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}$, with $0 \leq R_1 < R_2$ and $0 \leq \theta_1 < \theta_2 \leq 2\pi$.

Show that $\displaystyle \iint_D f(x,y) \,dA = \frac{1}{2} (R_2^2 - R_1^2) [H(\theta_2) - H(\theta_1)]$, where $H$ is an antiderivative of $h$.

63) Apply the preceding exercise to calculate the integral $\displaystyle \iint_D \frac{y^2}{x^2}\,dA,$ where $D = \big\{(r, \theta)\,|\, 1 \leq r \leq 2, \space \frac{\pi}{6} \leq \theta \leq \frac{\pi}{3}\big\}.$

Answer

$\sqrt{3} - \frac{\pi}{4}$

64) Let $f$ be a continuous function that can be expressed in polar coordinates as a function of $\theta$ only; that is $f(x,y) = g(r)h(\theta)$, where $(x,y) \in \big\{(r, \theta )\,|\,R_1 \leq r \leq R_2, \space \theta_1 \leq \theta \leq \theta_2\big\}$ with $0 \leq R_1 < R_2$ and $0 \leq \theta_1 < \theta_2 \leq 2\pi$. Show that $$\iint_D f(x,y)\,dA = [G(R_2) - G(R_1)] \space [H(\theta_2) - H(\theta_1)], \nonumber$$ where $G$ and $H$ are antiderivatives of $g$ and $h$, respectively.

65) Evaluate $\displaystyle \iint_D \arctan \left(\frac{y}{x}\right) \sqrt{x^2 + y^2}\,dA,$ where $D = \big\{(r,\theta)\,|\, 2 \leq r \leq 3, \space \frac{\pi}{4} \leq \theta \leq \frac{\pi}{3}\big\}$.

Answer

$\frac{133}{864}\pi^2$

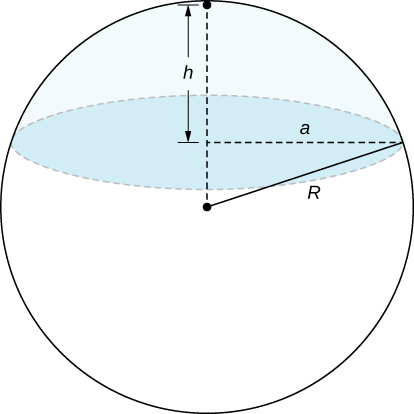
66) A spherical cap is the region of a sphere that lies above or below a given plane.

a. Show that the volume of the spherical cap in the figure below is $\frac{1}{6} \pi h (3a^2 + h^2)$.

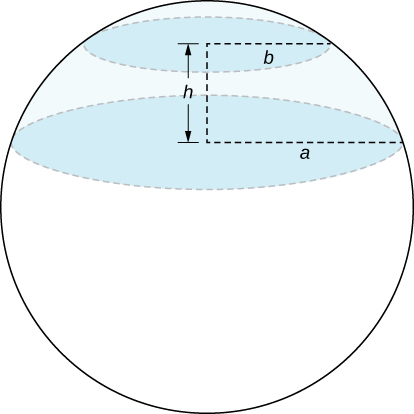
b. A spherical segment is the solid defined by intersecting a sphere with two parallel planes. If the distance between the planes is $h$ show that the volume of the spherical segment in the figure below is $\frac{1}{6}\pi h (3a^2 + 3b^2 + h^2)$.

67) In statistics, the joint density for two independent, normally distributed events with a mean $\mu = 0$ and a standard distribution $\sigma$ is defined by $p(x,y) = \frac{1}{2\pi\sigma^2} e^{-\frac{x^2+y^2}{2\sigma^2}}$. Consider $(X,Y)$, the Cartesian coordinates of a ball in the resting position after it was released from a position on the z-axis toward the $xy$-plane. Assume that the coordinates of the ball are independently normally distributed with a mean $\mu = 0$ and a standard deviation of $\sigma$ (in feet). The probability that the ball will stop no more than $a$ feet from the origin is given by $$P[X^2 + Y^2 \leq a^2] = \iint_D p(x,y) dy \space dx, \nonumber$$ where $D$ is the disk of radius $a$ centered at the origin. Show that $$P[X^2 + Y^2 \leq a^2] = 1 - e^{-a^2/2\sigma^2}. \nonumber$$

68) The double improper integral $$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx \nonumber$$ may be defined as the limit value of the double integrals $\displaystyle \iint_D e^{-x^2+y^2/2}\,dA$ over disks $D_a$ of radii $a$ centered at the origin, as $a$ increases without bound; that is,

$$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}dy \space dx = \lim_{a\rightarrow\infty} \iint_{D_a} e^{-x^2+y^2/2}\,dA. \nonumber$$

Use polar coordinates to show that $\displaystyle \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \, dx = 2\pi.$

69) Show that $\displaystyle \int_{-\infty}^{\infty} e^{-x^2/2}\,dx = \sqrt{2\pi}$ by using the relation

$$\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-x^2+y^2/2}\,dy \,dx = \left(\int_{-\infty}^{\infty} e^{-x^2/2}dx \right) \left( \int_{-\infty}^{\infty} e^{-y^2/2}dy \right). \nonumber$$

Contributors

• Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

• Problems 1, 2, 34 - 37 and 50 - 51 are from Apex Calculus, Chapter 13.3
• Edited by Paul Seeburger (Monroe Community College)