4.3E: Exercises

Last updated
Save as PDF

Page ID: 30395

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Practice Makes Perfect

Identify the x- and y- Intercepts on a Graph

In the following exercises, find the x- and y- intercepts on each graph.

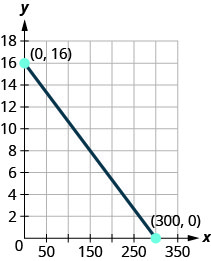
Exercise $\PageIndex{1}$

$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 5, 8), (negative 4, 7), (negative 3, 6), (negative 2, 5), (negative 1, 4), (0, 3), (1, 2), (2, 1), (3, 0), (4, negative 1), (5, negative 2) and (6, negative 3).$

Answer: (3,0),(0,3)

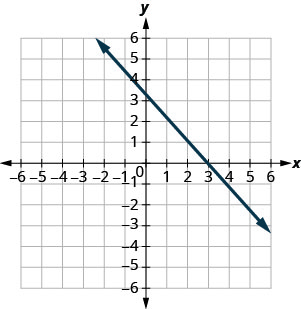
Exercise $\PageIndex{2}$

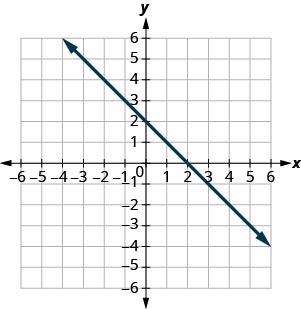
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, 8), (negative 5, 7), (negative 4, 6), (negative 3, 5), (negative 2, 4), (negative 1, 3), (0, 2), (1, 1), (2, 0), (3, negative 1), (4, negative 2), (5, negative 3) and (6, negative 4).$

Exercise $\PageIndex{3}$

$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 5, negative 10), (negative 4, negative 9), (negative 3, negative 8), (negative 2, negative 7), (negative 1, negative 6), (0, negative 5), (1, negative 4), (2, negative 3), (3, negative 2), (4, negative 1), (5, 0), (6, 1), (7, 2), and (8, 3).$

Answer: (5,0),(0,−5)

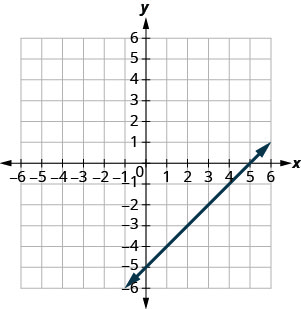
Exercise $\PageIndex{4}$

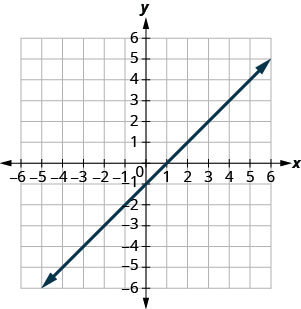
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 7), (negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), and (8, 7).$

Exercise $\PageIndex{5}$

$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 7), (negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), and (8, 7).$

Answer: (−2,0),(0,−2)

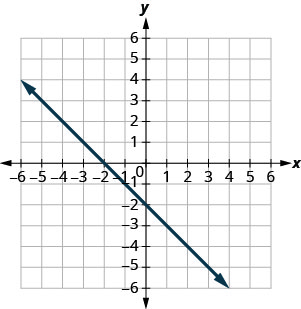
Exercise $\PageIndex{6}$

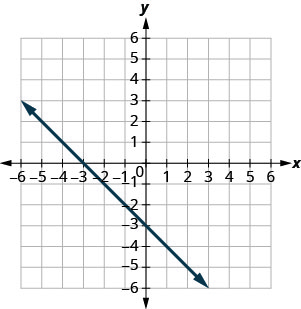
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, 3), (negative 5, 2), (negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), (4, negative 7), (5, negative 8), and (6, negative 9).$

Exercise $\PageIndex{7}$

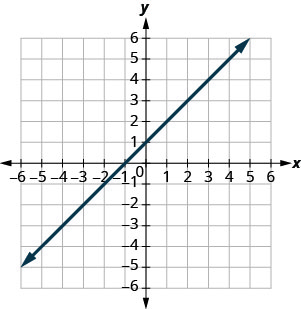
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 6, negative 5), (negative 5, negative 4), (negative 4, negative 3), (negative 3, negative 2), (negative 2, negative 1), (negative 1, 0), (0, 1), (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), and (8, 9).$

Answer: (−1,0),(0,1)

Exercise $\PageIndex{8}$

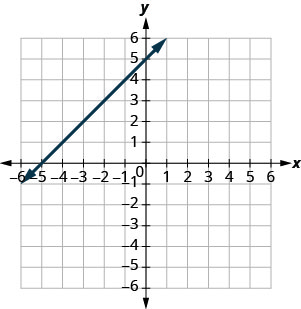
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 8, negative 3), (negative 7, negative 2), (negative 6, negative 1), (negative 5, 0), (negative 4, 1), (negative 3, 2), (negative 2, 3), (negative 1, 4), (0, 5), (1, 6), (2, 7), (3, 8), (4, 9), and (5, 10).$

Exercise $\PageIndex{9}$

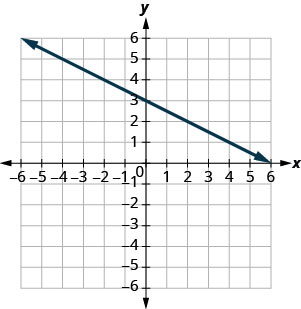
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 10 to 10. The y- axis of the planes runs from negative 10 to 10. The straight line goes through the points (negative 10, 8), (negative 8, 7), (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), (6, 0), (8, negative 1), and (10, negative 2).$

Answer: (6,0),(0,3)

Exercise $\PageIndex{10}$

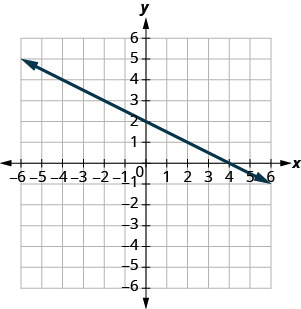
$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 6, 5), (negative 4, 4), (negative 2, 3), (0, 2), (2, 1), (4, 0), and (6, negative 1).$

Exercise $\PageIndex{11}$

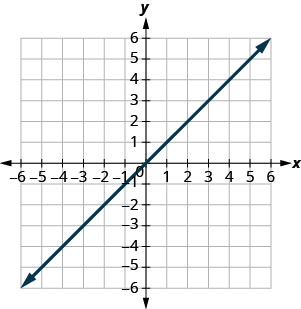
Answer: (0,0)

Exercise $\PageIndex{12}$

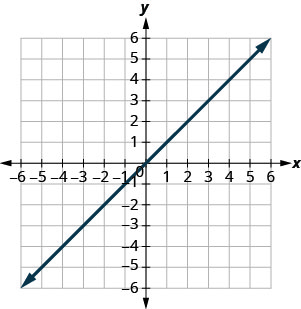
Find the x- and y- Intercepts from an Equation of a Line

In the following exercises, find the intercepts for each equation.

Exercise $\PageIndex{13}$

x+y=4

Answer: (4,0),(0,4)

Exercise $\PageIndex{14}$

x+y=3

Exercise $\PageIndex{15}$

x+y=−2

Answer: (−2,0),(0,−2)

Exercise $\PageIndex{16}$

x+y=−5

Exercise $\PageIndex{17}$

x–y=5

Answer: (5,0),(0,−5)

Exercise $\PageIndex{18}$

x–y=1

Exercise $\PageIndex{19}$

x–y=−3

Answer: (−3,0),(0,3)

Exercise $\PageIndex{20}$

x–y=−4

Exercise $\PageIndex{21}$

x+2y=8

Answer: (8,0),(0,4)

Exercise $\PageIndex{22}$

x+2y=10

Exercise $\PageIndex{23}$

3x+y=6

Answer: (2,0),(0,6)

Exercise $\PageIndex{24}$

3x+y=9

Exercise $\PageIndex{25}$

x–3y=12

Answer: (12,0),(0,−4)

Exercise $\PageIndex{26}$

x–2y=8

Exercise $\PageIndex{27}$

4x–y=8

Answer: (2,0),(0,−8)

Exercise $\PageIndex{28}$

5x–y=5

Exercise $\PageIndex{29}$

2x+5y=10

Answer: (5,0),(0,2)

Exercise $\PageIndex{30}$

2x+3y=6

Exercise $\PageIndex{31}$

3x–2y=12

Answer: (4,0),(0,−6)

Exercise $\PageIndex{32}$

3x–5y=30

Exercise $\PageIndex{33}$

$y=\frac{1}{3} x+1$

Answer: (-3,0),(0,1)

Exercise $\PageIndex{34}$

$y=\frac{1}{4} x-1$

Exercise $\PageIndex{35}$

$y=\frac{1}{5} x+2$

Answer: (−10,0),(0,2)

Exercise $\PageIndex{36}$

$y=\frac{1}{3} x+4$

Exercise $\PageIndex{37}$

y=3x

Answer: (0,0)

Exercise $\PageIndex{38}$

y=-2x

Exercise $\PageIndex{39}$

y=-4x

Answer: (0,0)

Exercise $\PageIndex{40}$

y=5x

Graph a Line Using the Intercepts

In the following exercises, graph using the intercepts.

Exercise $\PageIndex{41}$

$-x+5 y=10$

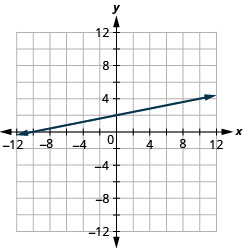
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The line graphed is negative x plus 5 y equals 10.$

Exercise $\PageIndex{42}$

$-x+4 y=8$

Exercise $\PageIndex{43}$

$x+2 y=4$

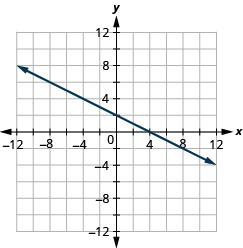
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, 6), (negative 6, 5), (negative 4, 4), (negative 2, 3), (0, 2), (2, 1), (4, 0), (6, negative 1), (8, negative 2), and (10, negative 3).$

Exercise $\PageIndex{44}$

$x+2 y=6$

Exercise $\PageIndex{45}$

$x+y=2$

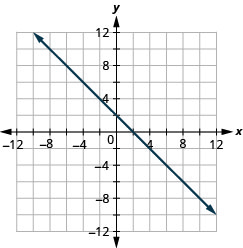
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, 10), (negative 7, 9), (negative 6, 8),(negative 5, 7), (negative 4, 6), (negative 3, 5), (negative 2, 4), (negative 1, 3), (0, 2), (1, 1), (2, 0), (3, negative 1), (4, negative 2), (5, negative 3), (6, negative 4), (7, negative 5), (8, negative 6), (9, negative 7), and (10, negative 8).$

Exercise $\PageIndex{46}$

$x+y=5$

Exercise $\PageIndex{47}$

$x+y=-3$

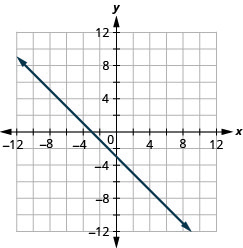
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 7, 4), (negative 6, 3), (negative 5, 2),(negative 4, 1), (negative 3, 0), (negative 2, negative 1), (negative 1, negative 2), (0, negative 3), (1, negative 4), (2, negative 5), (3, negative 6), and (4, negative 7).$

Exercise $\PageIndex{48}$

$x+y=-1$

Exercise $\PageIndex{49}$

$x-y=1$

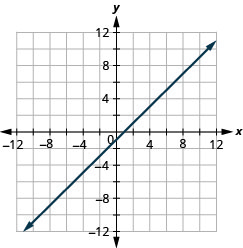
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 9), (negative 7, negative 8), (negative 6, negative 7),(negative 5, negative 6), (negative 4, negative 5), (negative 3, negative 4), (negative 2, negative 3), (negative 1, negative 2), (0, negative 1), (1, 0), (2, 1), (3, 2), (4, 3), (5, 4), (6, 5), (7, 6), (8, 7), (9, 8), and (10, 9).$

Exercise $\PageIndex{50}$

$x-y=2$

Exercise $\PageIndex{51}$

$x-y=-4$

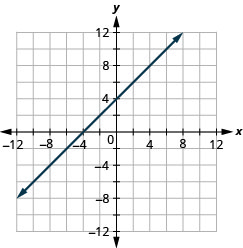
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 8, negative 4), (negative 7, negative 3), (negative 6, negative 2),(negative 5, negative 1), (negative 4, 0), (negative 3, 1), (negative 2, 2), (negative 1, 3), (0, 4), (1, 5), (2, 6), (3, 7), (4, 8), (5, 9), (6, 10), (7, 11), and (8, 12).$

Exercise $\PageIndex{52}$

$x-y=-3$

Exercise $\PageIndex{53}$

$4 x+y=4$

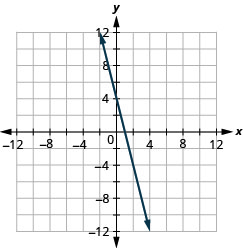
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 2, 12), (negative 1, 8), (0, 4), (1, 0), (2, negative 4), (3, negative 8), and (4, negative 12).$

Exercise $\PageIndex{54}$

$3 x+y=3$

Exercise $\PageIndex{55}$

$2 x+4 y=12$

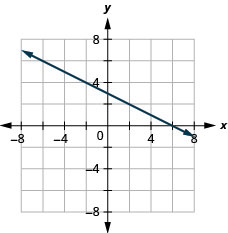
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 7 to 7. The y- axis of the planes runs from negative 7 to 7. The straight line goes through the points (negative 6, 6), (negative 4, 5), (negative 2, 4), (0, 3), (2, 2), (4, 1), and (6, 0).$

Exercise $\PageIndex{56}$

$3 x+2 y=12$

Exercise $\PageIndex{57}$

$3 x-2 y=6$

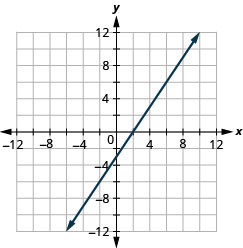
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 6, negative 12), (negative 4, negative 9), (negative 2, negative 6), (0, negative 3), (2, 0), (4, 3), (6, 6), (8, 9), and (10, 12).$

Exercise $\PageIndex{58}$

$5 x-2 y=10$

Exercise $\PageIndex{59}$

$2 x-5 y=-20$

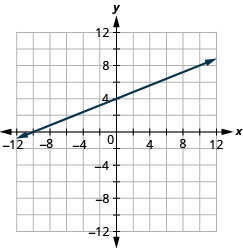
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, 0), (negative 5, 2), (0, 4), (5, 6), and (10, 8).$

Exercise $\PageIndex{60}$

$3 x-4 y=-12$

Exercise $\PageIndex{61}$

$3 x-y=-6$

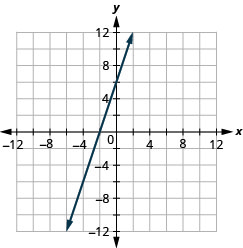
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 6, negative 12), (negative 5, negative 9), (negative 4, negative 6), (negative 3, negative 3), (negative 2, 0), (1, 3), (2, 6), (3, 9), and (4, 12).$

Exercise $\PageIndex{62}$

$2 x-y=-8$

Exercise $\PageIndex{63}$

$y=-2 x$

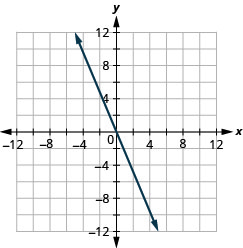
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 5, 10), (negative 4, 8), (negative 3, 6), (negative 2, 4), (negative 1, 2), (0, 0), (1, negative 2), (2, negative 4), (3, negative 6), (4, negative 8), (5, negative 10), and (6, negative 12)$

Exercise $\PageIndex{64}$

$y=-4 x$

Exercise $\PageIndex{65}$

$y=x$

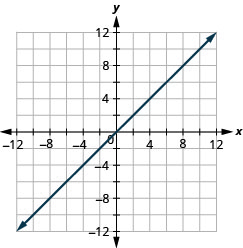
Answer: $The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from negative 12 to 12. The y- axis of the planes runs from negative 12 to 12. The straight line goes through the points (negative 10, 10), (negative 9, 9), (negative 8, 8), (negative 7, 7), (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3, 3), (negative 2, 2), (negative 1, 1), (0, 0), (1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6), (7, 7), (8, 8), (9, 9), and (10, 10)$

Exercise $\PageIndex{66}$

y=3x

Everyday Math

Exercise $\PageIndex{67}$

Road trip. Damien is driving from Chicago to Denver, a distance of 1000 miles. The x- axis on the graph below shows the time in hours since Damien left Chicago. The y- axis represents the distance he has left to drive.

$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from 0 to 16. The y- axis of the planes runs from 0 to 1200 in increments of 200. The straight line goes through the points (0, 1000), (3, 800), (6, 600), (9, 400), (12, 200), and (15, 0). The points (0, 1000) and (15, 0) are marked and labeled with their coordinates.$

Find the x- and y- intercepts.
Explain what the x- and y- intercepts mean for Damien.

Answer

(0,1000),(15,0)
At (0,1000), he has been gone 0 hours and has 1000 miles left. At (15,0), he has been gone 15 hours and has 0 miles left to go.

Exercise $\PageIndex{68}$

Road trip. Ozzie filled up the gas tank of his truck and headed out on a road trip. The x- axis on the graph below shows the number of miles Ozzie drove since filling up. The y- axis represents the number of gallons of gas in the truck’s gas tank.

$The figure shows a straight line on the x y- coordinate plane. The x- axis of the plane runs from 0 to 350 in increments of 50. The y- axis of the planes runs from 0 to 18 in increments of 2. The straight line goes through the points (0, 16), (150, 8), and (300, 0). The points (0, 16) and (300, 0) are marked and labeled with their coordinates$

Find the x- and y- intercepts.
Explain what the x- and y- intercepts mean for Ozzie.

Writing Exercises

Exercise $\PageIndex{69}$

How do you find the $x$ -intercept of the graph of $3 x-2 y=6 ?$

Answer: Answers will vary.

Exercise $\PageIndex{70}$

Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation 4x+y=−4? Why?

Exercise $\PageIndex{71}$

Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation $y=\frac{2}{3}x−2$? Why?

Answer: Answers will vary.

Exercise $\PageIndex{72}$

Do you prefer to use the method of plotting points or the method using the intercepts to graph the equation y=6? Why?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$The figure shows a table with four rows and four columns. The first row is a header row and it labels each column. The first column header is “I can…”, the second is "confidently", the third is “with some help”, “no minus I don’t get it!”. Under the first column are the phrases “identify the x and y intercepts of a graph”, “find the x and y intercepts from an equation of a line”, and “graph a line using intercepts”. Under the second, third, fourth columns are blank spaces where the learner can check what level of mastery they have achieved.$

ⓑ What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Practice Makes Perfect

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)

Exercise \(\PageIndex{61}\)

Exercise \(\PageIndex{62}\)

Exercise \(\PageIndex{63}\)

Exercise \(\PageIndex{64}\)

Exercise \(\PageIndex{65}\)

Exercise \(\PageIndex{66}\)

Everyday Math

Exercise \(\PageIndex{67}\)

Exercise \(\PageIndex{68}\)

Writing Exercises

Exercise \(\PageIndex{69}\)

Exercise \(\PageIndex{70}\)

Exercise \(\PageIndex{71}\)

Exercise \(\PageIndex{72}\)

Self Check