1.7.R: Trigonometric Identities and Equations (Review)
- Last updated
- May 6, 2021
- Save as PDF
- Page ID
- 62972
( \newcommand{\kernel}{\mathrm{null}\,}\)
7.1: Solving Trigonometric Equations with Identities
For the exercises 1-6, find all solutions exactly that exist on the interval [0,2π)
1) csc2t=3
- Answer
-
sin−1(√33),π−sin−1(√33),π+sin−1(√33),2π−sin−1(√33)
2) cos2x=14
3) 2sinθ=−1
- Answer
-
7π6,11π6
4) tanxsinx+sin(−x)=0
5) 9sinω−2=4sin2ω
- Answer
-
sin−1(14),π−sin−1(14)
6) 1−2tan(ω)=tan2(ω)
For the exercises 7-8, use basic identities to simplify the expression.
7) secxcosx+cosx−1secx
- Answer
-
1
8) sin3x+cos2xsinx
For the exercises 9-10, determine if the given identities are equivalent.
9) sin2x+sec2x−1=(1−cos2x)(1+cos2x)cos2x
- Answer
-
Yes
10) tan3xcsc2xcot2xcosxsinx=1
7.2: Sum and Difference Identities
For the exercises 1-4, find the exact value.
1) tan(7π12)
- Answer
-
−2−√3
2) cos(25π12)
3) sin(70∘)cos(25∘)−cos(70∘)sin(25∘)
- Answer
-
√22
4) cos(83∘)cos(23∘)+sin(83∘)sin(23∘)
For the exercises 5-6, prove the identity.
5) cos(4x)−cos(3x)cosx=sin2x−4cos2xsin2x
- Answer
-
cos(4x)−cos(3x)cosx=cos(2x+2x)−cos(x+2x)cosx=cos(2x)cos(2x)−sin(2x)sin(2x)−cosxcos(2x)cosx+sinxsin(2x)cosx=(cos2x−sin2x)2−4cos2xsin2x−cos2x(cos2x−sin2x)+sinx(2)sinxcosxcosx=(cos2x−sin2x)2−4cos2xsin2x−cos2x(cos2x−sin2x)+2sin2xcos2x=cos4x−2cos2xsin2x+sin4−cos2xsin2x−cos4x+cos2xsin2x+2sin2xcos2x=sin4x−4cos2xsin2x+cos2xsin2x=sin2x(sin2x+cos2x)−4cos2xsin2x=sin2x−4cos2xsin2x
6) cos(3x)−cos3x=−cosxsin2x−sinxsin(2x)
For exercise 7, simplify the expression.
7) tan(12x)+tan(18x)1−tan(18x)tan(12x)
- Answer
-
tan(58x)
For the exercises 8-9, find the exact value.
8) cos(sin−1(0)−cos−1(12))
9) tan(sin−1(0)−sin−1(12))
- Answer
-
√33
7.3: Double-Angle, Half-Angle, and Reduction Formulas
For the exercises 1-4, find the exact value.
1) Find sin(2θ), cos(2θ)
2) Find sin(2θ), cos(2θ), and tan(2θ) given secθ=−53 and θ is in the interval [π2,π].
- Answer
-
−2425,−725,247
3) sin(7π8)
4) sec(3π8)
- Answer
-
√2(2+√2)
For the exercises 5-6, use Figure below to find the desired quantities.
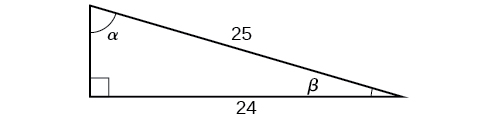
5) sin(2β),cos(2β),tan(2β),sin(2α),cos(2α),tan(2α)
6) sin(β2),cos(β2),tan(β2),sin(α2),cos(α2),tan(α2)
- Answer
-
√210,7√210,17,35,45,34
For the exercises 7-8, prove the identity.
7) 2cos(2x)sin(2x)=cotx−tanx
8) cotxcos(2x)=−sin(2x)+cotx
- Answer
-
cotxcos(2x)=cotx(1−2sin2x)=cotx−cosxsinx(2)sin2x=−2sinxcos=−sin(2x)+cotx
For the exercises 9-10, rewrite the expression with no powers.
9) cos2xsin4(2x)
10) tan2xsin3x
- Answer
-
10sinx−5sin(3x)+sin(5x)8(cos(2x)+1)
7.4: Sum-to-Product and Product-to-Sum Formulas
For the exercises 1-3, evaluate the product for the given expression using a sum or difference of two functions. Write the exact answer.
1) cos(π3)sin(π4)
2) 2sin(2π3)sin(5π6)
- Answer
-
√32
3) 2cos(π5)cos(π3)
For the exercises 4-5, evaluate the sum by using a product formula. Write the exact answer.
4) sin(π12)−sin(7π12)
- Answer
-
−√22
5) cos(5π12)+cos(7π12)
For the exercises 6-9, change the functions from a product to a sum or a sum to a product.
6) sin(9x)cos(3x)
- Answer
-
12(sin(6x)+sin(12x))
7) cos(7x)cos(12x)
8) sin(11x)+sin(2x)
- Answer
-
2sin(132x)cos(92x)
9) cos(6x)+cos(5x)
7.5: Solving Trigonometric Equations
For the exercises 1-2, find all exact solutions on the interval [0,2π).
1) tanx+1=0
- Answer
-
3π4,7π4
2) 2sin(2x)+√2=0
For the exercises 3-7, find all exact solutions on the interval [0,2π).
3) 2sin2x−sinx=0
- Answer
-
0,π6,5π6,π
4) cos2x−cosx−1=0
5) 2sin2x+5sinx+3=0
- Answer
-
3π2
6) cosx−5sin(2x)=0
7) 1sec2x+2+sin2x+4cos2x=0
- Answer
-
No solution.
For the exercises 8-9, simplify the equation algebraically as much as possible. Then use a calculator to find the solutions on the interval [0,2π)
8) √3cot2x+cotx=1
9) csc2x−3cscx−4=0
- Answer
-
0.2527,2.8889,4.7124
For the exercises 10-11, graph each side of the equation to find the zeroes on the interval [0,2π).
10) 20cos2x+21cosx+1=0
11) sec2x−2secx=15
- Answer
-
1.3694,1.9106,4.3726,4.9137
7.6: Modeling with Trigonometric Equations
For the exercises 1-3, graph the points and find a possible formula for the trigonometric values in the given table.
1)
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| y | 1 | 6 | 11 | 6 | 1 | 6 |
2)
| x | y |
|---|---|
| 0 | -2 |
| 1 | 1 |
| 2 | -2 |
| 3 | -5 |
| 4 | -2 |
| 5 | 1 |
- Answer
-
3sin(xπ2)−2
3)
| x | y |
|---|---|
| -3 | 3+2√2 |
| -2 | 3 |
| -1 | 2√2−1 |
| 0 | 1 |
| 1 | 3−2√2 |
| 2 | -1 |
| 3 | −1−2√2 |
4) A man with his eye level 6 feet above the ground is standing 3 feet away from the base of a 15-foot vertical ladder. If he looks to the top of the ladder, at what angle above horizontal is he looking?
- Answer
-
71.6∘
5) Using the ladder from the previous exercise, if a 6-foot-tall construction worker standing at the top of the ladder looks down at the feet of the man standing at the bottom, what angle from the horizontal is he looking?
For the exercises 6-7, construct functions that model the described behavior.
6) A population of lemmings varies with a yearly low of 500 in March. If the average yearly population of lemmings is 950, write a function that models the population with respect to t
- Answer
-
P(t)=950−450sin(π6t)
7) Daily temperatures in the desert can be very extreme. If the temperature varies from 90∘F to 30∘F and the average daily temperature first occurs at 10 AM, write a function modeling this behavior.
For the exercises 8-9, find the amplitude, frequency, and period of the given equations.
8) y=3cos(xπ)
- Answer
-
Amplitude: 3, period: 2, frequency: 12Hz
9) y=−2sin(16xπ)
For the exercises 10-11, model the described behavior and find requested values.
10) An invasive species of carp is introduced to Lake Freshwater. Initially there are 100 carp in the lake and the population varies by 20 fish seasonally. If by year 5, there are 625 carp, find a function modeling the population of carp with respect to t
- Answer
-
C(t)=20sin(2πt)+100(1.4427)t
11) The native fish population of Lake Freshwater averages 2500 fish, varying by 100 fish seasonally. Due to competition for resources from the invasive carp, the native fish population is expected to decrease by 5% each year. Find a function modeling the population of native fish with respect to t
Practice Test
For the exercises 1-2, simplify the given expression.
1) cos(−x)sinxcotx+sin2x
- Answer
-
1
2) sin(−x)cos(−2x)−sin(−x)cos(−2x)
For the exercises 3-6, find the exact value.
3) cos(7π12)
- Answer
-
√2−√64
4) tan(3π8)
5) tan(sin−1(√22)+tan−1√3)
- Answer
-
−√2−√3
6) 2sin(π4)sin(π6)
For the exercises 7-16, find all exact solutions to the equation on [0,2π).
7) cos2x−sin2x−1=0
- Answer
-
0,π
8) cos2x=cosx
- Answer
-
sin−1(14(√13−1)),π−sin−1(14(√13−1))
9) cos(2x)+sin2x=0
10) 2sin2x−sinx=0
- Answer
-
0,π6,5π6,π
11) Rewrite the expression as a product instead of a sum: cos(2x)+cos(−8x)
12) Find all solutions of tan(x)−√3=0.
- Answer
-
π3+kπ
13) Find the solutions of sec2x−2secx=15 on the interval [0,2π) algebraically; then graph both sides of the equation to determine the answer.
14) Find sin(2θ), cos(2θ), and tan(2θ) given cotθ=−34 and θ is on the interval [π2,π].
- Answer
-
−2425,−725,247
15) Find sin(θ2), cos(θ2), and tan(θ2) given cosθ=−725 and θ is in quadrant IV.
16) Rewrite the expression sin4x with no powers greater than 1.
- Answer
-
18(3+cos(4x)−4cos(2x))
For the exercises 17-19, prove the identity.
17) tan3x−tanxsec2x=tan(−x)
18) sin(3x)−cosxsin(2x)=cos2xsinx−sin3x
- Answer
-
sin(3x)−cosxsin(2x)=sin(x+2x)−cosx(2sinxcosx)=sinxcos(2x)+sin(2x)cosx−2sinxcos2x=sinx(cos2x−sin2x)+2sinxcosxcosx−2sinxcos2x=sinxcos2x−sin3x+0=cos2xsinx−sin3x=cos2xsinx−sin3x
19) sin(2x)sinx−cos(2x)cosx=secx
20) Plot the points and find a function of the form y=Acos(Bx+C)+D that fits the given data.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| y | -2 | 2 | -2 | 2 | -2 | 2 |
- Answer
-
y=2cos(πx+π)
21) The displacement h(t) in centimeters of a mass suspended by a spring is modeled by the function h(t)=14sin(120πt)
22) A woman is standing 300 feet away from a 2000-foot building. If she looks to the top of the building, at what angle above horizontal is she looking? A bored worker looks down at her from the 15th floor (1500 feet above her). At what angle is he looking down at her? Round to the nearest tenth of a degree.
- Answer
-
81.5∘,78.7∘
23) Two frequencies of sound are played on an instrument governed by the equation n(t)=8cos(20πt)cos(1000πt)
24) The average monthly snowfall in a small village in the Himalayas is 6 inches, with the low of 1 inch occurring in July. Construct a function that models this behavior. During what period is there more than 10 inches of snowfall?
- Answer
-
6+5cos(π6(1−x)). From November 23 to February 6.
25) A spring attached to a ceiling is pulled down 20 cm. After 3 seconds, wherein it completes 6 full periods, the amplitude is only 15 cm. Find the function modeling the position of the spring t seconds after being released. At what time will the spring come to rest? In this case, use 1 cm amplitude as rest.
26) Water levels near a glacier currently average 9 feet, varying seasonally by 2 inches above and below the average and reaching their highest point in January. Due to global warming, the glacier has begun melting faster than normal. Every year, the water levels rise by a steady 3 inches. Find a function modeling the depth of the water t months from now. If the docks are 2 feet above current water levels, at what point will the water first rise above the docks?
- Answer
-
D(t)=2cos(π6t)+108+14t, 93.5855 months (or 7.8 years) from now
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


