3.1: Inequalities in One Variable

Last updated

Jun 3, 2021
Save as PDF
- 3: Linear Programming
- 3.2: Linear Inequalities

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

When learning about domain and range, you learned about inequalities and using set-builder and interval notation to represent them. In this section, we will explore how to solve linear and absolute value inequalities in one variable. The process is very similar to solve equations, but instead of the solution being a single value, the solution will be an inequality.

Notice that if an inequality is true, like 2 < 5, then these operations result in a true statement as well, just like with equations:

Adding a number to both sides:

2 + 4 < 5 + 4 6 < 9 True

Subtracting a number on both sides:

2 – 3 < 5 – 3 -1 < 2 True

Multiplying a positive number on both sides:

2(3) < 5(3) 6 < 15 True

Dividing by a positive number on both sides:

2/2 < 5/2 1 < 2.5 True

We can use these operations just like when solving equations.

Example $\PageIndex{1}$

Solve $3x + 7 \geq 1 \nonumber$

Solution

$3x + 7 \geq 1\nonumber$

Subtract 7 from both sides

$3x \geq - 6\nonumber$

Divide both sides by 3

$x \geq - 2\nonumber$

This inequality represents the solution set. It tells us that all numbers greater than or equal to -2 will satisfy the original inequality. We could also write this solution in interval notation, as $[ - 2,\infty )$ .

$clipboard_e33a84754cdf650e94ed1830669bd960a.png$ To understand what is happening, we could also consider the problem graphically. If we were to graph the equation $y = 3x + 7$ , then solving $3x + 7 \geq 1$ would correspond with asking “for what values of $x$ is $y \geq 1$ ”. Notice that the part of the graph where this is true corresponds to where $x \geq - 2$ .

While most operations in solving inequalities are the same as in solving equations, we run into a problem when multiplying or dividing both sides by a negative number. Notice, for example:

2(-3) < 5(-3) -6 < -15 Not True

To account for this, when multiplying or dividing by a negative number, we must reverse the sign of the inequality.

Rules for Solving Linear Inequalities

You may add or subtract a positive or negative number to both sides of the inequality.
You can multiply or divide both sides of the inequality by a positive number.
You can multiply or divide both sides of the inequality by a negative number, but you must reverse the direction of the inequality.

Example $\PageIndex{2}$

Solve $12 - 4x < 6\nonumber$

Solution

$12 - 4x < 6\nonumber$

Subtract 12 from both sides

$- 4x < - 6\nonumber$

Divide both sides by -4, and reverse the inequality direction

$x > \frac{ - 6}{ - 4}\nonumber$

Simplify

$x > \frac{3}{2}\nonumber$

Exercise $\PageIndex{1}$

Solve: $6 + 2x \leq 18 + 5x\nonumber$

Answer: $x \geq - 4\nonumber$

Example $\PageIndex{3}$

A company spends $1200 per day on overhead and labor, and each item they produce costs $5 for materials. If they sell the items for $15 each, how many items will they need to sell each day for their profits to be positive?

Solution

While we could solve this problem using equations, it also lends itself to inequalities, since we want the profit to be positive: $P > 0$ .

Costs: $C(q) = 1200 + 5q$

Revenue: $R(q) = 10q$

Profit: $P(q) = 10q – (1200 + 5q) = 5q – 1200$

Solving $P(q) > 0$ :

$\begin{align*} 5q – 1200 &> 0 \\ 5q &> 1200 \\ q &> 240 \end{align*}$

The company will need to less at least 240 items a day to make a profit.

Compound Inequalities

Compound inequalities are inequalities that consist of more than one part. The most common type is called a tripartite inequality. The basic version looks like this:

$- 1 < 3x + 5 < 14\nonumber$ .

When we write these, it is important that both inequalities point in the same direction and that the “outside” inequality is also true – in this case $-1 < 14$ is true, so this is valid. Expressions like $10 < x < 2$ and $1 < x > 5$ are not valid notation.

The most universal way to solve a tripartite inequality is to:

Break it into two separate inequalities
Solve each inequality separately
Combine the solutions if possible.

Example $\PageIndex{4}$

Solve $- 1 < - 3x + 5 < 14\nonumber$

Solution

First we separate this into two inequalities:

$- 1 < - 3x + 5 \quad \text{and} \quad - 3x + 5 < 14\nonumber$

Now we solve each:

$- 6 < - 3x \quad \text{and} \quad -3x < 9\nonumber$

$2 > x\nonumber \quad \text{and} \quad x > - 3\nonumber$

Now we can combine these solution sets. The numbers where both $2 > x$ and $x > - 3$ are true is the set:

$2 > x > - 3\nonumber$

While this solution is valid and correct, it is more common to write the solution to tripartite inequalities with the smaller number on the left. We could rewrite the solution as:

$- 3 < x < 2\nonumber$

This also has the advantage of corresponding better with the answer in interval notation: $(-3, 2)$

With this particular inequality, it would also be possible to skip the step of breaking it apart, and instead just subtract 5 from all three “parts” of the inequality. This works for simple problems like this, but may fail if the inequality has variables in more than one “part” of the inequality.

Exercise $\PageIndex{2}$

Solve: $4 \leq 2x + 6 < 16\nonumber$

Answer

$-1 \leq x < 5 \nonumber$

In interval notation, this is $[-1, 5)$ .

Absolute Value

So far in this section we have been looking at inequalities that are linear. We will now turn to absolute value inequalities. The absolute value function is a piecewise-defined function made up of two linear functions.

Absolute Value of a Function

The absolute value function can be defined as

$f(x) = \left| x \right| = \left\{ \begin{array}{*{20}{c}} x & \text{ if }& x \geq 0 \\ - x& \text{ if }& x < 0\end{array} \right.\nonumber$

The graph of the absolute value looks like a V:

$clipboard_e403fef19c4d4cf4e49fa8213e04e9f56.png$

The absolute value function is commonly used to determine the distance between two numbers on the number line. Given two values $a$ and $b$ , then $\left| a - b \right|$ will give the distance, a positive quantity, between these values, regardless of which value is larger.

Example $\PageIndex{5}$

Describe all values, $x$ , within a distance of 4 from the number 5.

Solution

We want the distance between $x$ and 5 to be less than or equal to 4. The distance can be represented using the absolute value, giving the expression

$\left| x - 5 \right| \leq 4 \nonumber$

Example $\PageIndex{6}$

A 2010 poll reported 78% of Americans believe that people who are gay should be able to serve in the US military, with a reported margin of error of 3%[1]. The margin of error tells us how far off the actual value could be from the survey value[2]. Express the set of possible values using absolute values.

[1] http://www.pollingreport.com/civil.htm, retrieved August 4, 2010

[2] Technically, margin of error usually means that the surveyors are 95% confident that actual value falls within this range.

Solution

Since we want the size of the difference between the actual percentage, $p$ , and the reported percentage to be less than 3%,

$\left| p - 78 \right| \leq 3 \nonumber$

Exercise $\PageIndex{3}$

Students who score within 20 points of 80 will pass the test. Write this as a distance from 80 using the absolute value notation.

Answer: Using the variable $p$ , for passing, $\left| {p - 80} \right| \leq 20 \nonumber$

Solving Absolute Value Equations

To solve an equation like $8 = \left| 2x - 6 \right|$ , we can notice that the absolute value will be equal to eight if the quantity inside the absolute value were 8 or -8. This leads to two different equations we can solve independently:

$\begin{align*} 2x - 6 &= 8 \\ 2x &= 14 \\ x &= 7 \end{align*}$

$\begin{align*} 2x - 6 &= - 8\\ 2x &= - 2 \\ x &= - 1 \end{align*}$

Solutions to Absolute Value Equations

An equation of the form $\left|A \right| = B$ , with $B \geq 0$ , will have solutions when

$A = B \quad \text{or} \quad A = -B \nonumber$

Example $\PageIndex{7}$

Solve: $0 = \left| 4x + 1 \right| - 7$

Solution

$0 = \left| {4x + 1} \right| - 7\nonumber$

Isolate the absolute value on one side of the equation

$7 = \left| {4x + 1} \right| \nonumber$

Now we can break this into two separate equations:

$\begin{align*} 7 &= 4x + 1 \\ 6 &= 4x \\ x &= \frac{6}{4} = \frac{3}{2} \end{align*}$

$\begin{align*} - 7 &= 4x + 1 \\ - 8 &= 4x \\ x &= \frac{- 8}{4} = - 2 \end{align*}$

There are two solutions: $x = \frac{3}{2}$ and $x = -2$ .

Example $\PageIndex{8}$

Solve $1 = 4\left| x - 2 \right| + 2$

Solution

Isolating the absolute value on one side the equation,

$\begin{align*} 1 &= 4\left| x - 2 \right| + 2 \\ -1 &= 4\left| x - 2 \right| \\ - \frac{1}{4} &= \left| x - 2 \right| \end{align*}$

At this point, we notice that this equation has no solutions – the absolute value always returns a positive value, so it is impossible for the absolute value to equal a negative value.

Exercise $\PageIndex{4}$

Find the horizontal & vertical intercepts for the function $f(x) = - \left| {x + 2} \right| + 3$

Answer

Horizontal: $(1,0)$ and $(-5,0 )$

Vertical: $(0,1)$

Solving Absolute Value Inequalities

When absolute value inequalities are written to describe a set of values, like the inequality $\left| x - 5 \right| \leq 4$ we wrote earlier, it is sometimes desirable to express this set of values without the absolute value, either using inequalities, or using interval notation.

We will explore two approaches to solving absolute value inequalities:

Using a graph
Using test values

Example $\PageIndex{9}$

Solve $\left| {x - 5} \right| \leq 4 \nonumber$

Solution

With both approaches, we will need to know first where the corresponding equality is true. In this case we first will find where $\left| {x - 5} \right| = 4$ . We do this because the absolute value is a nice friendly function with no breaks, so the only way the function values can switch from being less than 4 to being greater than 4 is by passing through where the values equal 4. Solve $\left| {x - 5} \right| = 4$ ,

$\begin{align*} x - 5 &= 4 \\ x &= 9 \end{align*}$

$\begin{align*} x - 5 = - 4 \\ x = 1 \end{align*}$

To use a graph, we can sketch the function $f(x) = \left| {x - 5} \right|$ . To help us see where the outputs are 4, the line $g(x) = 4$ could also be sketched.

$clipboard_ec4f582027da58a971239b05a48935ef4.png$

On the graph, we can see that indeed the output values of the absolute value are equal to 4 at $x = 1$ and $x = 9$ . Based on the shape of the graph, we can determine the absolute value is less than or equal to 4 between these two points, when $1 \leq x \leq 9$ . In interval notation, this would be the interval $[1,9]$ .

As an alternative to graphing, after determining that the absolute value is equal to 4 at $x = 1$ and $x = 9$ , we know the graph can only change from being less than 4 to greater than 4 at these values. This divides the number line up into three intervals: $x<1, 1<x<9$ , and $x>9$ . To determine when the function is less than 4, we could pick a value in each interval and see if the output is less than or greater than 4.

$\begin{array}{llll} \text { Interval } & \text { Test } x & f(x) & <4 \text { or }>4 ? \\ \hline x<1 & 0 & |0-5|=5 & \text { greater } \\ 1<x<9 & 6 & |6-5|=1 & \text { less } \\ x>9 & 11 & |11-5|=6 & \text { greater } \end{array} \nonumber$

Since $1 \leq x \leq 9$ is the only interval in which the output at the test value is less than 4, we can conclude the solution to $\left| {x - 5} \right| \leq 4$ is $1 \leq x \leq 9$ .

Example $\PageIndex{10}$

Given the function $f(x) = - \frac{1}{2}\left| {4x - 5} \right| + 3$ , determine for what $x$ values the function values are negative.

Solution

We are trying to determine where $f(x) < 0$ , which is when $- \frac{1}{2}\left| {4x - 5} \right| + 3 < 0$ . We begin by isolating the absolute value:

$- \frac{1}{2}\left| {4x - 5} \right| < - 3 \nonumber$

When we multiply both sides by -2, it reverses the inequality,

$\left| {4x - 5} \right| > 6 \nonumber$

Next we solve for the equality $\left| {4x - 5} \right| = 6$

$\begin{align*} 4x - 5 &= 6 \\ 4x &= 11 \\ x &= \frac{11}{4} \end{align*} \nonumber$

$\begin{align*} 4x - 5 &= - 6 \\ 4x &= - 1 \\ x &= \frac{- 1}{4} \end{align*}$

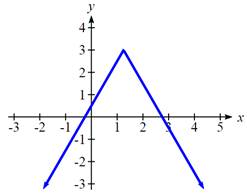
$clipboard_e6e8fecc9efffa079ad9a37eaaedde4a0.png$

We can now either pick test values or sketch a graph of the function to determine on which intervals the original function value are negative. Notice that it is not even really important exactly what the graph looks like, as long as we know that it crosses the horizontal axis at $x = \frac{- 1}{4}$ and $x = \frac{11}{4}$ , and that the graph has been flipped.

From the graph of the function, we can see the function values are negative to the left of the first horizontal intercept at $x = \frac{ - 1}{4}$ , and negative to the right of the second intercept at $x = \frac{11}{4}$ . This gives us the solution to the inequality:

$x < \frac{-1}{4}\quad \text{or} \quad x > \frac{11}{4}\nonumber$

In interval notation, this would be $\left( - \infty ,\frac{ - 1}{4} \right) \cup \left( \frac{11}{4},\infty \right)$

Exercise $\PageIndex{6}$

Solve $- 2\left| k - 4 \right| \leq - 6$

Answer: $k < 1$ or $k > 7$ ; in interval notation this would be $\left( -\infty ,1 \right) \cup \left( 7,\infty \right)$

There is a third approach to solving absolute value inequalities that is formulaic. While it works, and you are welcome to use it, it is much more likely that you will remember the other approaches.

Solutions to Absolute Value Inequalities

To solve $\left| A \right| < B$ , solve: $- B < A < B$

To solve $\left| A \right| > B$ , solve: $A > B$ or $A < - B$

Example $\PageIndex{11}$

Solve $3\left| x + 4 \right| - 2 \geq 7$

Solution

We need to start by isolating the absolute value:

$3\left| {x + 4} \right| - 2 \geq 7\nonumber$

Add 2 to both sides

$3\left| {x + 4} \right| \geq 9\nonumber$

Divide both sides by 3

$\left| {x + 4} \right| \geq 3\nonumber$

Now we can break this apart and solve each piece separately:

$\begin{align*} x + 4 &\geq 3\nonumber \\ x &\geq - 1\end{align*}$

$\begin{align*} x + 4 &\leq - 3 \\ x &\leq - 7 \end{align*}$

In interval notation, this would be $( -\infty , -7] \cup [ -1,\infty )$ .

Important Topics of this Section

The properties of the absolute value function

Solving absolute value equations

Finding intercepts

Solving absolute value inequalities

Search

Text Color

Text Size

Margin Size

Font Type

Compound Inequalities

Absolute Value

Solving Absolute Value Equations

Solving Absolute Value Inequalities

Support Center

How can we help?