4.1: Quadratic Functions

In this section, we will explore the quadratic functions, a type of polynomial function.  Quadratics commonly arise from problems involving areas, as well as revenue and profit, providing some interesting applications.

Example $\PageIndex{1}$:

A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side. Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length $L$.

Solution

Let’s use a diagram such as Figure $\PageIndex{10}$ to record the given information. It is also helpful to introduce a temporary variable, $W$, to represent the width of the garden and the length of the fence section parallel to the backyard fence.

Figure $\PageIndex{10}$: Diagram of the garden and the backyard.

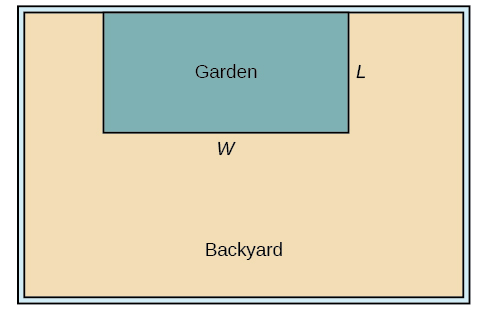
In a scenario like this involving geometry, it is often helpful to draw a picture.  It might also be helpful to introduce a temporary variable, $W$, to represent the side of fencing parallel to the 4^th side or backyard fence. 

Since We know we have only 80 feet of fence available, and $L+W+L=80$, or more simply, $2L+W=80$. This allows us to represent the width, $W$, in terms of $L$.

$$W=80−2L$$

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

$$\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}$$

This formula represents the area of the fence in terms of the variable length $L$.

Short run Behavior: Vertex

We now explore the interesting features of the graphs of quadratics.  In addition to intercepts, quadratics have an interesting feature where they change direction, called the vertex. 

The standard form for a quadratic is $f(x) = a{x^2} + bx + c$, but you will often see them written in the form $f(x) = a{(x - h)^2} + k$.  To see why, consider this example.

Example $\PageIndex{2}$

Sketch a graph of $g(x) = \frac{1}{2}(x + 2)^2 - 3$

Solution

We can create a table of values, which we can use to plot several points and connect them with a smooth curve.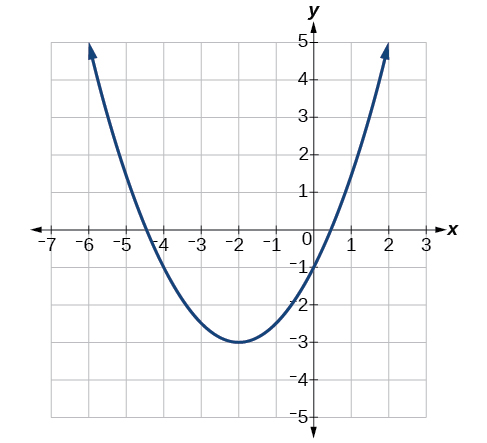

$x$	$g(x)$
-5	1.5
-4	-1
-3	-2.5
-2	-3
-1	-2.5
0	-1
1	1.5

 

Notice that the turning point of the graph, where it changes from decreasing to increasing, is at the point $(-2, -3)$.  We call this point the vertex of the quadratic.  Notice that $g(x) = \frac{1}{2}(x + 2)^2 - 3$ can also be written as $g(x) = \frac{1}{2}\left( x - ( -2) \right)^2 - 3$.  Comparing that to the form $f(x) = a{(x - h)^2} + k$, you can see that the vertex of the graph, $(-2, -3)$, corresponds with the point $h, k$.

Definitions: Forms of Quadratic Functions

• The standard form of a quadratic function is $f(x)=ax^2+bx+c$.
• The vertex form of a quadratic function is $f(x)=a(x−h)^2+k$.
• The vertex of the quadratic function is located at $(h,k)$, where $h$ and $k$ are the numbers in the vertex form of the function.

When $a>0$, the graph of the quadratic will open upwards.

When $a<0$, the graph of the quadratic will open downwards.

Exercise $\PageIndex{1}$

A coordinate grid has been superimposed over the quadratic path of a basketball. Find an equation for the path of the ball. Does the shooter make the basket?

Figure $\PageIndex{8}$: Stop motioned picture of a boy throwing a basketball into a hoop to show the parabolic curve it makes.
(credit: modification of work by Dan Meyer)

Answer

The path passes through the origin and has vertex at $(−4, 7)$, so $h(x)=–\frac{7}{16}(x+4)^2+7$. To make the shot, $h(−7.5)$ would need to be about 4 but $h(–7.5){\approx}1.64$; he doesn’t make it.

Example $\PageIndex{3}$

Write $g(x) = \frac{1}{2}{(x + 2)^2} - 3$ in standard form.

Solution

To write this in standard polynomial form, we could expand the formula and simplify terms:

$$\begin{align*}  g(x) &= \frac{1}{2}{(x + 2)^2} - 3   \\  g(x) &= \frac{1}{2}(x + 2)(x + 2) - 3   \\  g(x) &= \frac{1}{2}({x^2} + 4x + 4) - 3   \\  g(x) &= \frac{1}{2}{x^2} + 2x + 2 - 3   \\  g(x) &= \frac{1}{2}{x^2} + 2x - 1   \end{align*}$$

In the previous example, we saw that it is possible to rewrite a quadratic function given in vertex form and rewrite it in standard form by expanding the formula.  It would be useful to reverse this process, since the transformation form reveals the vertex.

Expanding out the general transformation form of a quadratic gives:

$$\begin{align*}  f(x) &= a{(x - h)^2} + k = a(x - h)(x - h) + k   \\  f(x) &= a({x^2} - 2xh + {h^2}) + k = a{x^2} - 2ahx + a{h^2} + k   \end{align*}$$

This should be equal to the standard form of the quadratic:

$$a{x^2} - 2ahx + a{h^2} + k = a{x^2} + bx + c \nonumber$$

 

The second degree terms are already equal.  For the linear terms to be equal, the coefficients must be equal:

$$- 2ah = b, \quad  \text{so} \quad  h = -\frac{b}{2a} \nonumber$$

This provides us a method to determine the horizontal shift of the quadratic from the standard form.  We could likewise set the constant terms equal to find:

$$\begin{align*} a{h^2} + k &= c \\ k &= c - a{h^2} \\ k&= c - a\left(  - \frac{b}{2a} \right)^2 \\ k&= c - a\frac{b^2}{4a^2} \\ k&= c - \frac{b^2}{4a}\end{align*}$$

In practice, though, it is usually easier to remember that $k$ is the output value of the function when the input is $h$, so $k=f(h)$.

Finding the Vertex of a Quadratic

For a quadratic given in standard form, the vertex $(h, k)$ is located at:

$$h =  - \frac{b}{2a},\quad    k = f(h) = f\left(\frac{-b}{2a} \right) \nonumber$$

Example $\PageIndex{4}$

Find the vertex of the quadratic $f(x) = 2{x^2} - 6x + 7$.  Rewrite the quadratic into vertex form.

Solution

The horizontal coordinate of the vertex will be at $h =  - \frac{b}{2a} =  - \frac{- 6}{2(2)} = \frac{6}{4} = \frac{3}{2}$

The vertical coordinate of the vertex will be at $f\left(\frac{3}{2} \right) = 2\left( \frac{3}{2} \right)^2 - 6\left( \frac{3}{2} \right) + 7 = \frac{5}{2}$

Rewriting into vertex form, the value of a will remain the same as in the original quadratic. 

$$f(x) = 2{\left( {x - \frac{3}{2}} \right)^2} + \frac{5}{2} \nonumber$$

Exercise $\PageIndex{2}$

Given the equation $g(x)=13+x^2−6x$, write the equation in standard form and then vertex form.

Answer

$g(x)=x^2−6x+13$ in standard form; $g(x)=(x−3)^2+4$ in vertex form.

In addition to enabling us to more easily graph a quadratic written in standard form, finding the vertex serves another important purpose – it allows us to determine the maximum or minimum value of the function, depending on which way the graph opens.

Example $\PageIndex{5}$: Finding the Domain and Range of a Quadratic Function

Returning to our backyard farmer from the beginning of the section, what dimensions should she make her garden to maximize the enclosed area?

Solution

Earlier we determined the area she could enclose with 80 feet of fencing on three sides was given by the equation $A(L) = 80L - 2{L^2}$.  Notice that quadratic has been vertically reflected, since the coefficient on the squared term is negative, so the graph will open downwards, and the vertex will be a maximum value for the area.

In finding the vertex, we take care since the equation is not written in standard polynomial form with decreasing powers.  But we know that a is the coefficient on the squared term, so $a = -2$, b = 80, and $c = 0$. 

Finding the vertex:

$$h =  - \frac{80}{2( - 2)} = 20,   k = A(20) = 80(20) - 2(20)^2 = 80.0 \nonumber$$

The maximum value of the function is an area of 800 square feet, which occurs when $L = 20$ feet.  When the shorter sides are 20 feet, that leaves 40 feet of fencing for the longer side.  To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet, and the longer side parallel to the existing fence has length 40 feet.

Example $\PageIndex{6}$

A local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Solution

Revenue is the amount of money a company brings in.  In this case, the revenue can be found by multiplying the charge per subscription times the number of subscribers.  We can introduce variables, $C$ for charge per subscription and $S$ for the number subscribers, giving us the equation:

Revenue = $CS$

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently $S=84,000$ and $C=30$, and that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, $C=32$ and $S=79,000$. From this we can find a linear equation relating the two quantities. Treating $C$ as the input and $S$ as the output, the equation will have the form

$$S = mC+b\nonumber$$

The slope will be

$$\begin{align*} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align*}$$

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the vertical intercept.

$$\begin{align*} S&=−2500C+b &\text{Plug in the point $S=84,000$ and $C=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align*}$$

This gives us the linear equation $S=−2,500C+159,000$ relating cost and subscribers. We now return to our revenue equation.

$$\begin{align*} \text{Revenue}&=CS \\ \text{Revenue}&=C(−2,500C+159,000) \\ \text{Revenue}&=−2,500C^2+159,000C \end{align*}$$

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

$$\begin{align*} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align*}$$

The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

$$\begin{align*} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align*}$$

Notice that the equation $S =  - 2,500C + 159,000$ we found in the last example is essentially a demand function – a relationship between the price $(C)$ and the demand $(S)$. This is a common type of economic application.

Maximizing Revenue or Profit

To solve a problem involving maximizing revenue or profit given data on demand at different price levels,

1. Use the data provided to create a demand equation relating price and quantity demanded.  This will usually be a linear function.
2. Create a Revenue equation.  Start with Revenue = price times quantity, then substitute the demand equation to create a revenue equation just in terms of quantity.
3. If the problem is to maximize profit, create a Profit equation.  Profit = revenue minus cost.
4. Find the vertex of the Revenue or Profit function to find the quantity that maximizes revenue or profit.
5. If needed, use that quantity with the demand function to find the price that maximizes revenue or profit.

Example $\PageIndex{7}$

A company is planning to sell a new smart fitness device.  Developing the product will cost $700,000, and each product will cost $30 to manufacture.  Market research suggests that if they sell the device for $100, they will be able to sell 30,000 items.  For each $10 they lower the price, they estimate they will sell 5,000 more items.  Assuming quantity demanded is linearly related to price, determine the price that will maximize profit

Solution

Let $p$ be the price per item, and $q$ be the quantity the company can sell.  We start by creating a linear demand function, of the form $p = mq + b$.

If they sell the device for $100, they will be able to sell 30,000 items, giving the point (30000, 100). 

We are told that for each $10 they lower the price, they estimate they will sell 5,000 more items.  We can either directly interpret this as a slope, or use it to create a second point.  Lowering the price to $90 would raise the quantity sold to 35,000, giving a second point (35000, 90).

Finding the slope:

$$m = \frac{90 - 100}{35000 - 30000} = \frac{- 10}{5000} =  - \frac{1}{500} =  - 0.002 \nonumber$$

The demand equation will look like $p =  - 0.002q + b$.  Substituting in (30000, 10) to solve for $b$:

$$\begin{align*} 100 &=  - 0.002(30000) + b   \\ 100 &=  -60 + b   \\  b &= 160   \\ \end{align*}  \nonumber$$

We now have our demand function:  $p =  - 0.002q + 160$.

 

Now we construct our revenue function, using our demand curve

$$\begin{align*} R &= pq & \quad  \text{Substituting in the demand function for} p \\ R &= \left( { - 0.002q + 160} \right)q =  - 0.002{q^2} + 160q &\end{align*}$$

Now looking at costs, we know the fixed costs are $700,000, and the per-item costs are $30, leading to the cost equation

$$C = 700,000 + 30q \nonumber$$

Finally we can construct the profit equation:

Profit = Revenue – Cost

$$\begin{align*}  P &= ( - 0.002{q^2} + 160q) - (700,000 + 30q)   \\  P &=  - 0.002{q^2} + 160q - 700,000 - 30q   \\  P &=  - 0.002{q^2} + 130q - 700,000   \end{align*}  \nonumber$$

Now to find the maximum we find the vertex of the quadratic:

$$h =  - \frac{130}{2( - 0.002)} = 32,500 \nonumber$$

To find the price that will produce a demand of 32,500 items, we use the demand function:

$$p =  - 0.002(32500) + 160 = 95 \nonumber$$

To maximize profit, the company should price the device at $95.  At that price they should expect to sell 35,000 items, with a total profit of:

$$P =  - 0.002{(32500)^2} + 130(32500) - 700,000 = \$ 1,412,500 \nonumber$$

Short run Behavior: Intercepts

 

As with any function, we can find the vertical intercepts of a quadratic by evaluating the function at an input of zero, and we can find the horizontal intercepts by solving for when the output will be zero.  Notice that depending upon the location of the graph, we might have zero, one, or two horizontal intercepts.

 

zero horizontal intercepts	one horizontal intercept	two horizontal intercepts

Example $\PageIndex{8}$: Finding the x-Intercepts of a Parabola

Find the vertical and horizontal intercepts of the quadratic $f(x) = 3{x^2} + 5x - 2$.

Solution

We can find the vertical intercept by evaluating the function at an input of zero:

$f(0) = 3{(0)^2} + 5(0) - 2 =  - 2$               Vertical intercept at $(0,-2)$

For the horizontal intercepts, we solve for when the output will be zero

$0 = 3{x^2} + 5x - 2$

In this case, the quadratic can be factored easily, providing the simplest method for solution

$$\begin{align*} 0 &= (3x - 1)(x + 2) \\ 0 &= 3x - 1   \\  x &= \frac{1}{3} \\ &\text{or}  \\  0 &= x + 2   \\  x &=  - 2  \end{align*}$$
Horizontal intercepts at $\left( {\frac{1}{3},0} \right)$ and (-2,0)

Notice that in the standard form of a quadratic, the constant term c reveals the vertical intercept of the graph.

For quadratics that can’t be factored, we need another technique.  Based on our previous work we showed that any quadratic in standard form can be written into vertex form as:
$$\begin{align*} &0 = a\left( x + \frac{b}{2a} \right)^2 + c - \frac{b^2}{4a} & \quad &\text{   start to solve for $x$ by moving the constants to the other side } \\& \frac{b^2}{4a} - c = a\left( x + \frac{b}{2a} \right)^2 & \quad &\text{           divide both sides by $a$ } \\& \frac{b^2}{4a^2} - \frac{c}{a} = \left(x + \frac{b}{2a} \right)^2 & \quad &\text{        find a common denominator to combine fractions } \\& \frac{b^2}{4a^2} - \frac{4ac}{4a^2} = \left( x + \frac{b}{2a} \right)^2 & \quad &\text{       combine the fractions on the left side of the equation } \\& \frac{b^2 - 4ac}{4a^2} = \left(x + \frac{b}{2a} \right)^2 & \quad &\text{        take the square root of both sides } \\& \pm \sqrt {\frac{b^2 - 4ac}{4a^2}}  = x + \frac{b}{2a}& \quad &\text{ subtract $b/2a$ from both sides } \\& -\frac{b}{2a} \pm \frac{\sqrt {b^2 - 4ac}}{2a} = x & \quad &\text{      combining the fractions } \\& x = \frac{- b \pm \sqrt {b^2 - 4ac}}{2a} & \quad &\text{              Notice that this can yield two different answers for $x$} \end{align*}$$

Quadratic Formula

For a quadratic function given in standard form $f(x) = a{x^2} + bx + c$, the quadratic formula gives the horizontal intercepts of the graph of this function.

$$x = \frac{ - b \pm \sqrt {{b^2} - 4ac} }{2a}\nonumber$$

Example $\PageIndex{9}$

A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation $H(t)=−16t^2+80t+40$.

When does the ball reach the maximum height?
What is the maximum height of the ball?
When does the ball hit the ground?

The ball reaches the maximum height at the vertex of the parabola.
$$\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}$$

The ball reaches a maximum height after 2.5 seconds.

To find the maximum height, find the y-coordinate of the vertex of the parabola.
$$\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}$$

The ball reaches a maximum height of 140 feet.

To find when the ball hits the ground, we need to determine when the height is zero, $H(t)=0$.

We use the quadratic formula.

$$\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align}$$

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

$$t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458$$

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.

Example $\PageIndex{10}$

The supply for a certain product can be modeled by $p = 3{q^2}$ and the demand can be modeled by $p = 1620 - 2{q^2}$, where $p$ is the price in dollars, and $q$ is the quantity in thousands of items.  Find the equilibrium price and quantity.

Solution

Recall that the equilibrium price and quantity is found by finding where the supply and demand curve intersect.  We can find that by setting the equations equal:

$$\begin{align*} 3q^2 &= 1620 - 2{q^2}\quad && \quad  \text{Add  $2{q^2}$ to both sides}  \\5q^2 &= 1620 \quad && \quad  \text{Divide by 5 on both sides}  \\q^2 &= 324 \quad && \quad  \text{Take the square root of both sides}  \\q &= \pm \sqrt {324} \quad &&  \\ &= \pm 18 \quad  && \end{align*}$$

Since it doesn’t make sense to talk about negative quantities, the equilibrium quantity is $q = 18$.  To find the equilibrium price, we evaluate either function at the equilibrium quantity.

$$p = 3{(18)^2} = 972 \nonumber$$

The equilibrium is 18 thousand items, at a price of $972.

Exercise $\PageIndex{4}$

For these two equations determine if the vertex will be a maximum value or a minimum value.

          a.  $g(x) =  - 8x + {x^2} + 7$

          b.  $g(x) =  - 3{(3 - x)^2} + 2$

Answer

a. Vertex is a minimum value

b. Vertex is a maximum value

Important Topics of this Section

Quadratic functions

         Standard form

         Transformation form/Vertex form

         Vertex as a maximum / Vertex as a minimum

Short run behavior

         Vertex / Horizontal & Vertical intercepts

Quadratic formula

 

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.