3.4: Continuity

Intuitively, a curve \(y = f(x)\) is continuous if it forms an unbroken line, that is, whenever \(x_{1}\) is close to \(x_{2}\), \(f\left(x_{1}\right)\) is close to \(f\left(x_{2}\right)\). To make this intuitive idea into a mathematical definition, we substitute “infinitely close” for “close”.

Definition:

\(f\) is said to be continuous at a point \(c\) if:

\(\begin{align*} &(\text{i}) \ && f \text{ is defined at } c; \\ &(\text{ii}) && \text{whenever } x \text{ is infinitely close to } c, f(x) \text{ is infinitely close to } f(c). \end{align*}\)

If \(f\) is not continuous at \(c\) it is said to be discontinuous at \(c\).

When \(f\) is continuous at \(c\), the entire part of the curve where \(x \approx c\) will be visible in an infinitesimal microscope aimed at the point \((c, f(c))\), as shown in Figure \(\PageIndex{1(\text{a})}\). But if \(f\) is discontinuous at \(c\), some values of \(f(x)\) where \(x \approx c\) will either be undefined or outside the range of vision of the microscope, as in Figure \(\PageIndex{1(\text{b})}\).

Continuity, like the derivative, can be expressed in terms of limits. Again the proof is immediate from the definitions.

Figure \(\PageIndex{1}\): Continuous and discontinuous functions.

Theorem \(\PageIndex{1}\)

\(f\) is continuous at \(c\) if and only if \[\lim_{x \rightarrow c} f(x) = f(c). \nonumber\]

As an application, we have a set of rules for combining continuous functions. They can be proved either by the corresponding rules for limits (Table \(\PageIndex{1}\) in Section 3.3) or by computing standard parts.

Theorem \(\PageIndex{2}\)

Suppose \(f\) and \(g\) are continuous at \(c\).

\(\begin{align*} &(\text{i}) \ &&\text{For any constant } k, \text{ the function } k \cdot f(x) \text{ is continuous at } c. \\ &(\text{ii}) \ &&f(x) + g(x) \text{ is continuous at } c. \\ &(\text{iii}) \ &&f(x) \cdot g(x) \text{ is continuous at } c. \\ &(\text{iv}) \ &&\text{If } g(c) \neq 0, \text{then } f(x) / g(x) \text{ is continuous at } c. \\ &(\text{v}) \ && \text{If } f(c) \text{ is positive and } n \text{is an integer, then } \sqrt[n]{f(x)} \text{ is continuous at } c. \end{align*}\)

By repeated use of Theorem \(\PageIndex{2}\), we see that all of the following functions are continuous at \(c\).

• Every polynomial function.
• Every rational function \(f(x) / g(x)\), where \(f(x)\) and \(g(x)\) are polynomials and \(g(c) \neq 0\).
• The functions \(f(x) = x^{r}\), where \(r\) is rational and \(x\) is positive.

Sometimes a function \(f(x)\) will be undefined at a point \(x = c\) while the limit \[L = \lim_{x \rightarrow c} f(x). \nonumber\]exists. When this happens, we can make the function continuous at \(c\) by defining \(f(c) = L\).

Example \(\PageIndex{1}\)

Let \(f(x) = \dfrac{x^{2} + x - 2}{x - 1}\).

At any point \(c \neq 1\) \(f\) is continuous. But \(f(1)\) is undefined so \(f\) is discontinuous at 1. However, \[\lim_{x \rightarrow 1} \frac{x^{2} + x - 2}{x - 1} = \lim_{x \rightarrow 1} \frac{(x - 1)(x + 2)}{x - 1} = 3. \nonumber\]

We can make \(f\) continuous at \(1\) by defining \[f(x) = \begin{cases} \frac{x^{2} + x - 2}{x - 1} \quad &\text{if } x \neq 1, \\ 3 &\text{if } x = 1. \end{cases} \nonumber\]

(See Figure \(\PageIndex{2}\).)

Figure \(\PageIndex{2}\): Defining a piecewise function that avoids discontinuity. 

In terms of a dependent variable \(y = f(x)\), the definition of continuity takes the following form, where \(\Delta y = f(c + \Delta x) - f(c)\).

Definition:

\(y\) is continuous at \(x = c\) if: 

\(\begin{align*} &(\text{i}) \ &&y \text{ is defined at } c. \\ &(\text{ii}) \ &&\text{Whenever } \Delta x \text{ is infinitesimal, } \Delta y \text{ is infinitesimal}. \end{align*}\)

To summarize, given a function \(y = f(x)\) defined at \(x = c\), all the statements below are equivalent.

1. \(f\) is continuous at \(c\).
2. Whenever \(x \approx c\), \(f(x) \approx f(c)\).
3. Whenever \(st(x) = c\), \(st(f(x)) = f(c)\).
4. \(\displaystyle \lim_{x \rightarrow c} f(x) = f(c)\).
5. \(y\) is continuous at \(x = c\).
6. Whenever \(\Delta x\) is infinitesimal, \(\Delta y\) is infinitesimal.

Our next theorem is that differentiability implies continuity. That is, the set of differentiable functions at \(c\) is a subset of the set of continuous functions at \(c\). (See Figure \(\PageIndex{3}\).)

Figure \(\PageIndex{3}\).

Theorem \(\PageIndex{3}\)

If \(f\) is differentiable at \(c\) then \(f\) is continuous at \(c\).

Proof

Let \(y = f(x)\), and let \(\Delta x\) be a nonzero infinitesimal. Then \(\Delta y/\Delta x\) is infinitely close to \(f'(c)\) and is therefore finite. Thus \(\Delta y = \Delta x(\Delta y/\Delta x)\) is the product of an infinitesimal and a finite number, so \(\Delta y\) is infinitesimal.

For example, the transcendental functions \(\sin x\), \(\cos x\), \(e^{x}\) are continuous for all \(x\), and \(\ln x\) is continuous for \(x > 0\). Theorem \(\PageIndex{3}\) can be used to show that combinations of these functions are continuous.

Example \(\PageIndex{2}\)

Find as large a set as you can on which the function \[f(x) = \frac{\sin x \ln (x + 1)}{x^{2} - 4} \nonumber\]is continuous.

Solution

\(\sin x\) is continuous for all \(x\). \(\ln (x + 1)\) is continuous whenever \(x + 1 > 0\), that is, \(x > - 1\). The numerator \(\sin x \ln (x + 1)\) is thus continuous whenever \(x > -1\). The denominator \(x^{2} - 4\) is continuous for all \(x\) but is zero when \(x = \pm 2\). Therefore \(f(x)\) is continuous whenever \(x > -1\) and \(x \neq 2\).

The next two examples give functions which are continuous but not differentiable at a point \(c\).

Example \(\PageIndex{3}\)

The function \(y = x^{1/3}\) is continuous but not differentiable at \(x = 0\). (See Figure \(\PageIndex{4 \text{(a)}\).) We have seen before that it is not differentiable at \(x = 0\). It is continuous because if \(\Delta x\) is infinitesimal then so is \[\Delta y = (0 + \Delta x)^{1/3} - 0^{1/3} = (\Delta x)^{1/3}. \nonumber\]

Example \(\PageIndex{4}\)

The absolute value function \(y = |x|\) is continuous but not differentiable at the point \(x = 0\). (See Figure \(\PageIndex{4 \text{(b)}\).) 

We have already shown that the derivative does not exist at \(x = 0\). To see that the function is continuous, we note that for any infinitesimal \(\Delta x\), \[\Delta y = |0 + \Delta x| - |0| = \Delta x. \nonumber\]and thus \(\Delta y\) is infinitesimal.

Figure \(\PageIndex{4}\): Graphs of (a) \(y = x^{1/3}\) and (b) \(y = |x|\).

The path of a bouncing ball is a series of parabolas shown in Figure \(\PageIndex{5}\). The curve is continuous everywhere. At the points \(a_{1}, a_{2}, a_{3}, \ldots\) where the ball bounces, the curve is continuous but not differentiable. At other points, the curve is both continuous and differentiable.

Figure \(\PageIndex{5}\): Path of bouncing ball.

In the classical kinetic theory of gases, a gas molecule is assumed to be moving at a constant velocity in a straight line except at the instant of time when it collides with another molecule or the wall of the container. Its path is then a broken line in space, as in Figure \(\PageIndex{6}\).

Figure \(\PageIndex{6}\): Path of an ideal gas molecule.

The position in three dimensional space at time \(t\) can be represented by three functions \[x= f(t), \quad y = g(t), \quad z = h(t). \nonumber\]

All three functions, \(f\), \(g\), and \(h\) are continuous for all values of \(t\). At the time \(t\) of a collision, at least one and usually all three derivatives \(dx/dt\), \(dy/dt\),(dz/dt\) will be undefined because the speed or direction of the molecule changes abruptly. At any other time \(t\), when no collision is taking place, all three derivatives \(dx/dt\), \(dy/dt\), \(dz/dt\) will exist.

The functions we shall ordinarily encounter in this book will be defined and have a derivative at all but perhaps a finite number of points of an interval. The graph of such a function will be a smooth curve where the derivative exists. At points where the curve has a sharp corner (like \(0\) in \(|x|\)) or a vertical tangent line (like \(0\) in \(x^{1/3}\)), the function is continuous but not differentiable (see Figure \(\PageIndex{7}\)). At points where the function is undefined or there is a jump, or the value approaches infinity or oscillates wildly, the function is discontinuous (see Figure \(\PageIndex{8}\)).

Figure \(\PageIndex{7}\): Points where \(f\) is continuous but nondifferentiable.

Figure \(\PageIndex{8}\): Points where \(f\) is discontinuous.

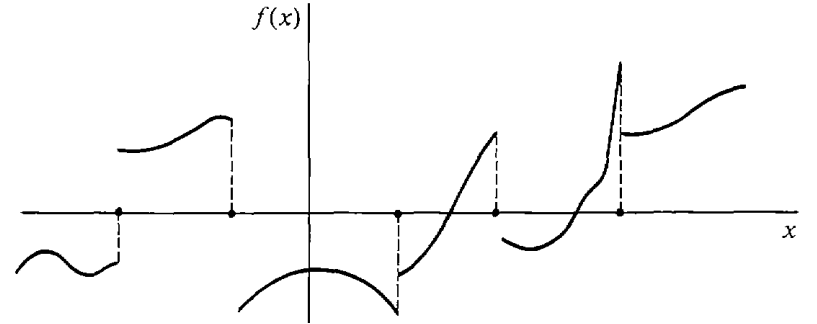
The next theorem is similar to the Chain Rule for derivatives.

Theorem \(\PageIndex{4}\)

If \(f\) is continuous at \(c\) and \(G\) is continuous at \(f(c)\), then the function \[g(x) = G(j(x)) \nonumber\]is also continuous at \(c\). That is, a continuous function of a continuous function is continuous.

Proof

Let \(x\) be infinitely close to but not equal to \(c\). Then \[st(g(x)) = st(G(j(x))) = G(st(f(x))) = G(j(c)) = g(c). \nonumber\]For example, the following functions are continuous: \[\begin{align*} f(x) &= \sqrt{x^{2} + 1} \quad &&\text{all } x \\ g(x) &= \left|x^{3} - x\right| &&\text{all } x \\ h(x) &= \left(1 + \sqrt{x}\right)^{1/3} &&x > 0 \\ j(x) &= e^{\sin x} && \text{all } x \\ k(x) &= \ln |x| &&\text{all } x \neq 0 \end{align*}\]

Here are two examples illustrating two types of discontinuities.

Example \(\PageIndex{5}\)

The function \(g(x) = \dfrac{x^{2} - 3x + 4}{4(x-1)(x-2)}\) is continuous at every real point except \(x = 1\) and \(x = 2\). At these two points
\(g(x)\) is undefined (Figure \(\PageIndex{9}\)).

Figure \(\PageIndex{9}\): Graph of \(y = \dfrac{x^{2} - 3x + 4}{4(x-1)(x-2)}\).

Example \(\PageIndex{6}\)

The greatest integer function \([x]\), shown in Figure \(\PageIndex{10}\), is defined by \[[x] = \text{the greatest integer } n \text{ such that } n \leq x. \nonumber\]Thus \([x] = 0\) if \(0 \leq x < 1\), \([x] = 1\) if \(1 \leq x < 2\), \([x] = 2\) if \(2 \leq x < 3\), and so on. For negative \(x\), we have \([x] = -1\) if \(-1 \leq x < 0\), \([x] = -2\) if \(-2 \leq x < -1\), and so on. For example, if \(-2 \leq x < -1\), and so on. For example, \[[7.362] = 7, \quad [\pi] = 3, \quad [-2.43] = -3. \nonumber\]

For each integer \(n\), \([n]\) is equal to \(n\). The function \([x]\) is continuous when \(x\) is not an integer but is discontinuous when \(x\) is an integer \(n\). At an integer \(n\), both one-sided limits exist but are different, \[\lim_{x \rightarrow n^{-}} f(x) = n - 1, \quad \lim_{x \rightarrow n^{+}} f(x) = n. \nonumber\]

The graph of \([x]\) looks like a staircase. It has a step, or jump discontinuity, at each integer \(n\). The function \([x]\) will be useful in the last section of this chapter. Some hand calculators have a key for either the greatest integer function or for the similar function that gives \([x]\) for positive \(x\) and \([x] + 1\) for negative \(x\).

Figure \(\PageIndex{10}\): Graph of the greatest integer function, \(y = [x]\).

Functions which are "continuous on an interval" will play an important role in this chapter. Intervals were discussed in Section 1.1. Recall that closed intervals have the form
\[[a, b], \nonumber\]

open intervals have one of the forms \[(a, b), \quad (a, \infty), \quad (-\infty, b), \quad (-\infty, \infty), \nonumber\]and half-open intervals have one of the forms \[[a, b), \quad (a, b], \quad [a, \infty), \quad (-\infty, b]. \nonumber\]In these intervals, \(a\) is called the lower endpoint and \(b\), the upper endpoint. The symbol \(-\infty\) indicates that there is no lower endpoint, while \(\infty\) indicates that there is no upper endpoint.

Definition:

We say that \(f\) is continuous on an open interval \(I\) if \(f\) is continuous at every point \(c\) in \(I\). If in addition \(f\) has a derivative at every point of \(I\), we say that \(f\) is differentiable on \(I\).

To define what is meant by a function continuous on a closed interval, we introduce the notions of continuous from the right and continuous from the left, using one-sided limits.

Definition:

\(f\) is continuous from the right at \(c\) if \(\displaystyle \lim_{x \rightarrow c^{+}} f(x) = f(c).\)

\(f\) is continuous from the left at \(c\) if \(\displaystyle \lim_{x \rightarrow c^{-}} f(x) = f(c).\)

Example \(\PageIndex{6}\) (continued)

The greatest integer function \(f(x) = [x]\) is continuous from the right but not from the left at each integer \(n\) because \[[n] = n, \quad \lim_{x \rightarrow n^{+}} [x] = n, \quad \lim_{x \rightarrow n^{-}} [x] = n - 1. \nonumber\]

It is easy to check that \(f\) is continuous at \(c\) if and only if \(f\) is continuous from both the right and left at \(c\).

Definition:

\(f\) is said to be continuous on the closed interval \([a, b]\) if \(f\) is continuous at each point \(c\) where \(a < c < b\), continuous from the right at \(a\), and continuous from the left at \(b\).

Figure \(\PageIndex{11}\) shows a function \(f\) continuous on \([a, b]\).

Figure \(\PageIndex{11}\): \(f\) is continuous on the interval \([a, b]\).

Example \(\PageIndex{7}\)

The semicircle \[y = \sqrt{1 - x^{2}} \nonumber\]shown in Figure \(\PageIndex{12}\) is continuous on the closed interval \([-1, 1]\). It is differentiable on the open interval \((-1, 1)\). To see that it is continuous from the right at \(x = -1\), let \(\Delta x\) be positive infinitesimal. Then \[\begin{align*} y &= \sqrt{1 - (-1)^{2}} = 0 \\ y + \Delta y &= \sqrt{1 - (-1 + \Delta x)^{2}} = \sqrt{1 - (1 - 2\Delta x + (\Delta x)^{2})} \\ &= \sqrt{2 \Delta x - (\Delta x)^{2}} = \sqrt{(2 - \Delta x)\Delta x}. \end{align*}\]

Thus \[y = \sqrt{(2 - \Delta x) \Delta x}. \nonumber\]The number inside the radical is positive infinitesimal, so \(\Delta y\) is infinitesimal. This shows that the function is continuous from the right at \(x = - 1\). Similar reasoning shows it is continuous from the left at \(x = 1\).

Figure \(\PageIndex{12}\): Graph of \(y = \sqrt{1 - x^{2}}\).

Problems for Section 3.4

In Problems 1-17, find the set of all points at which the function is continuous.

1.	\(f(x) = 3x^{2} + 5x + 4\)	2.	\(f(x) = \dfrac{5x + 2}{x^{2} + 1}\)
3.	\(f(x) = \sqrt{x + 2}\)	4.	\(f(x) = \dfrac{x}{x + 2}\)
5.	\(f(x) = \sqrt{|x - 2| + 1}\)	6.	\(f(x) = \dfrac{x + 3}{|x + 3|}\)
7.	\(f(x) = \dfrac{x}{x^{2} + x}\)	8.	\(f(x) = \dfrac{x + 2}{(x - 1)(x - 3)^{1/3}}\)
9.	\(f(x) = \sqrt{4 - x^{2}}\)	10.	\(f(x) = \sqrt{x^{2} - 4}\)
11.	\(f(x) = \dfrac{1}{x - (1/(x + 1))}\)	12.	\(g(x) = \dfrac{1}{x} + \dfrac{1}{x - 1}\)
13.	\(g(x) = \dfrac{x - 2}{x - 3} + \dfrac{x - 3}{x - 2}\)	14.	\(g(x) = \sqrt{x^{3} - x}\)
15.	\(g(x) = \sqrt[4]{x^{2} - x^{3}}\)	16.	\(f(t) = \sqrt{t^{-2} - 1}\)
17.	\(f(x) = \sqrt{t^{-1} - 1}\)
18.	Show that \(f(x) = \sqrt{x}\) is continuous from the right at \(x = 0\).
19.	Show that \(f(x) = \sqrt{1 - x}\) is continuous from the left at \(x = 1\).
20.	Show that \(f(x) = \sqrt{1 - |x|}\) is continuous on the closed interval \([- 1, 1]\).
21.	Show that \(f(x) = \sqrt{x} + \sqrt{2 - x}\) is continuous on the closed interval \([0, 2]\).
22.	Show that \(f(x) = \sqrt{9 - x^{2}}\) is continuous on the closed interval \([-3, 3]\).
23.	Show that \(f(x) = \sqrt{x^{2} - 9}\) is continuous on the half-open intervals \((-\infty, - 3]\) and \([3, \infty)\)).
\(\square\) 24.	Suppose the function \(f(x)\) is continuous on the closed interval \([a, b]\). Show that there is a function \(g(x)\) which is continuous on the whole real line and has the value \(g(x) = f(x)\) for \(x\) in \([a, b]\).
\(\square\) 25.	Suppose \(\displaystyle \lim_{x \rightarrow c} f(x) = L\). Prove that the function \(g(x)\), defined by \(g(x) = f(x)\) for \(x \neq c\) and \(g(x) = L\) for \(x = c\), is continuous at \(c\).
26.	In the curve \(y = f(x)\) illustrated below, identify the points \(x = c\) where each of the following happens: (a) \(f\) is discontinuous at \(x = c\) (b) \(f\) is continuous but not differentiable at \(x = c\).