3.9: Rational Inequalities
- Page ID
- 193570
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Rational inequalities are solved with the same three-step process that was used to solve the polynomial before. That is, in step 1, we find the solution of the corresponding equality, and then, in step 2, we use sample points of the graph to determine the intervals of the solution. Finally, in step 3, we check the endpoints of each interval.
Solve for \(x\).
\(\dfrac{x^2-5x+6}{x^2-5x}\geq 0\)
Solution
Here is the graph of \(\dfrac{x^2-5x+6}{x^2-5x}\) in the standard window.
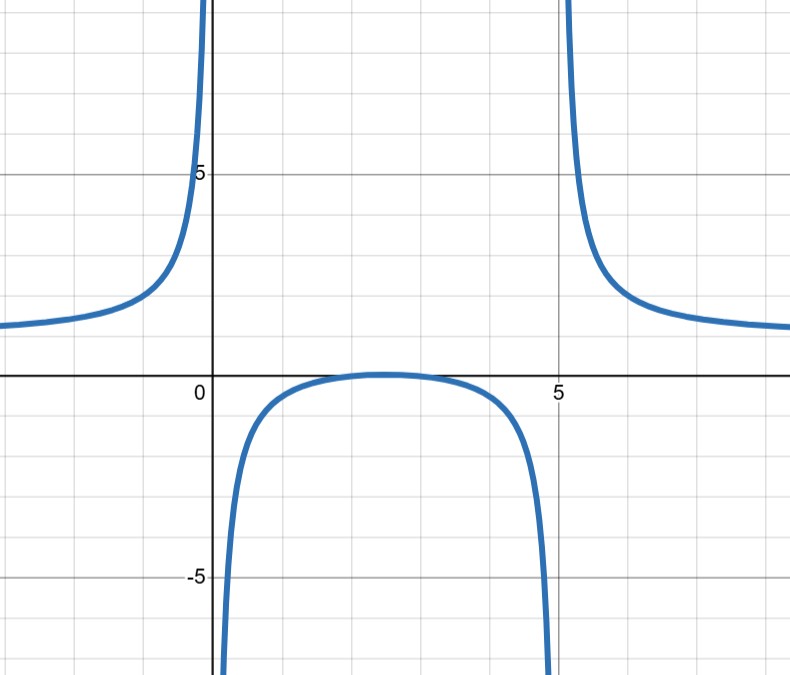
Factoring numerator and denominator, we can determine vertical asymptotes, holes, and \(x\)-intercepts.
\[\dfrac{x^2-5x+6}{x^2-5x}=\dfrac{(x-2)(x-3)}{x(x-5)} \nonumber \]
The vertical asymptotes are at \(x=0\) and \(x=5\), the \(x\)-intercepts are at \(x=2\) and \(x=3\). Since for large \(x\), the fraction reduces to \(\dfrac{x^2}{x^2}=1\), we see that the horizontal asymptote is at \(y=1\). Thus, \(\dfrac{x^2-5x+6}{x^2-5x}\geq 0\) for \(x< 0\) and \(x>5\). To see where the graph is \(\geq 0\) between \(0\) and \(5\), we zoom into the graph:
Combining all of the above information, we obtain the solution set:
\[\text{solution set}=(-\infty,0)\cup[2,3]\cup(5,\infty) \nonumber \]
Notice that the \(x-\)coordinate of the \(x-\)intercepts are \(x=2\) and \(x=3\) are included in the solution set, whereas the values \(x=0\) and \(x=5\) associated with the vertical asymptotes are not included since the fraction is not defined for \(x=0\) and \(x=5\).
Solve for \(x\).
\(\dfrac{5}{x-2}\leq 3\)
Solution
- To find the numbers \(x\) where \(\dfrac{5}{x-2}\leq 3\), we recommend rewriting the inequality so that one side becomes zero. Then, we graph the function on the other side of the new inequality.
\[\begin{aligned} \dfrac{5}{x-2}\leq 3 &\implies \quad \dfrac{5}{x-2}-3\leq 0 \implies \quad \dfrac{5-3(x-2)}{x-2}\leq 0\\ & \implies \quad \dfrac{5-3x+6}{x-2}\leq 0 \implies \quad \dfrac{11-3x}{x-2}\leq 0\end{aligned} \nonumber \]
Therefore, we graph the function \(f(x)=\dfrac{11-3x}{x-2}\).
The vertical asymptote is \(x=2\), and the \(x\)-intercept found thus
\[11-3x=0\implies \quad 11=3x \implies \quad x=\dfrac {11}{3} \nonumber \]
This together with the graph and the fact that \(f\) is undefined at \(2\) and \(f(\dfrac{11}{2})=0\) gives the following solution set:
\[\text{solution set}=\Big(-\infty,2\Big)\cup \Big[\dfrac{11}{3},\infty\Big) \nonumber \]
Solve for \(x\).
\(\dfrac{4}{x+5}<\dfrac{3}{x-3}\)
- \(|2x-3|>7\)
Solution
We want to find those numbers \(x\) for which \(\dfrac{4}{x+5}<\frac{3}{x-3}\). One way to do this is given by graphing both functions \(f_1(x)=\dfrac{4}{x+5}\) and \(f_2(x)=\dfrac{3}{x-3}\), and by trying to determine where \(f_1(x)<f_2(x)\). However this can sometimes be quite confusing, as the two graphs for \(f_1\) and \(f_2\) show below. As before, we recommend rewriting the inequality so that one side of the inequality becomes zero: We therefore graph the function \(f(x)=\(\dfrac{4}{x+5}-\dfrac{3}{x-3}<0\) or we can simplify to find a single fraction.
\[\begin{aligned} \dfrac{4}{x+5}<\dfrac{3}{x-3} & \implies \dfrac{4}{x+5}-\dfrac{3}{x-3} <0 \implies \quad \dfrac{4(x-3)-3(x+5)}{(x+5)(x-3)} <0 \\ & \implies \dfrac{4x-12-3x-15}{(x+5)(x-3)} <0 \implies \quad \dfrac{x-27}{(x+5)(x-3)}<0 \end{aligned} \nonumber \]
We therefore graph the function \(f(x)=\dfrac{x-27}{(x+5)(x-3)}\)
The vertical asymptotes of \(f(x)=\dfrac{x-27}{(x+5)(x-3)}\) are \(x=-5\) and \(x=3\). The \(x\)-intercept is \((27,0)\). We see from the graph that \(f(x)<0\) for \(x<-5\). To see the graph at \(x>3\), we zoom to the \(x\)-intercept at \(x=27\).
Therefore, the solution set is
\[\text{solution set}=\{x| x<-5,\text{ or } 3<x<27\}=(-\infty,-5)\cup (3,27) \nonumber \]
(The \(x\)-intercept \(x=27\) is not included in the solution set since the original equation had a “\(<\)” and not “\(\leq\)” sign.)