7.3: Adding and Subtracting Radical Expressions

Learning Objectives

• Add and subtract like radicals.
• Simplify radical expressions involving like radicals.

Adding and Subtracting Like Radicals

Adding and subtracting radical expressions is similar to adding and subtracting like terms. Radicals are considered to be like radicals¹⁶, or similar radicals¹⁷, when they share the same index and radicand. For example, the terms \(2\sqrt{6}\) and \(5\sqrt{6}\) contain like radicals and can be added using the distributive property as follows:

\(\begin{aligned} 2 \sqrt { 6 } + 5 \sqrt { 6 } & = ( 2 + 5 ) \sqrt { 6 } \\ & = 7 \sqrt { 6 } \end{aligned}\)

Typically, we do not show the step involving the distributive property and simply write,

\(2 \sqrt { 6 } + 5 \sqrt { 6 } = 7 \sqrt { 6 }\)

When adding terms with like radicals, add only the coefficients; the radical part remains the same.

Example \(\PageIndex{1}\):

Add: \(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 }\).

Solution

The terms are like radicals; therefore, add the coefficients.

\(7 \sqrt [ 3 ] { 5 } + 3 \sqrt [ 3 ] { 5 } = 10 \sqrt [ 3 ] { 5 }\)

Answer:

\(10 \sqrt [ 3 ] { 5 }\)

Subtraction is performed in a similar manner.

Example \(\PageIndex{2}\):

Subtract: \(4 \sqrt { 10 } - 5 \sqrt { 10 }\).

Solution

\(\begin{aligned} 4 \sqrt { 10 } - 5 \sqrt { 10 } & = ( 4 - 5 ) \sqrt { 10 } \\ & = - 1 \sqrt { 10 } \\ & = - \sqrt { 10 } \end{aligned}\)

Answer:

\(- \sqrt { 10 }\)

If the radicand and the index are not exactly the same, then the radicals are not similar and we cannot combine them.

Example \(\PageIndex{3}\):

Simplify: \(10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 }\).

Solution

\(\begin{aligned} 10 \sqrt { 5 } + 6 \sqrt { 2 } - 9 \sqrt { 5 } - 7 \sqrt { 2 } & = \color{Cerulean}{10 \sqrt { 5 } - 9 \sqrt { 5 }}\color{black}{ +}\color{OliveGreen}{ 6 \sqrt { 2 } - 7 \sqrt { 2 }} \\ & = \sqrt { 5 } - \sqrt { 2 } \end{aligned}\)

We cannot simplify any further because \(\sqrt{5}\) and \(\sqrt{2}\) are not like radicals; the radicands are not the same.

Answer:

\(\sqrt { 5 } - \sqrt { 2 }\)

\(\color{YellowOrange}{\text{Caution:}}\) It is important to point out that \(\sqrt { 5 } - \sqrt { 2 } \neq \sqrt { 5 - 2 }\). We can verify this by calculating the value of each side with a calculator.

\(\begin{array} { c } { \sqrt { 5 } - \sqrt { 2 } \approx 0.82 } \\ { \sqrt { 5 - 2 } = \sqrt { 3 } \approx 1.73 } \end{array}\)

In general, note that \(\sqrt [ n ] { a } \pm \sqrt [ n ] { b } \neq \sqrt [ n ] { a \pm b }\).

Example \(\PageIndex{4}\):

Simplify: \(5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 }\).

Solution

\(\begin{aligned} 5 \sqrt [ 3 ] { 10 } + 3 \sqrt { 10 } - \sqrt [ 3 ] { 10 } - 2 \sqrt { 10 } & =\color{Cerulean}{ 5 \sqrt [ 3 ] { 10 } - \sqrt [ 3 ] { 10 }}\color{black}{ +}\color{OliveGreen}{ 3 \sqrt { 10 } - 2 \sqrt { 10 }} \\ & = 4 \sqrt [ 3 ] { 10 } + \sqrt { 10 } \end{aligned}\)

We cannot simplify any further, because \(\sqrt [ 3 ] { 10 }\) and \(\sqrt { 10 }\) are not like radicals; the indices are not the same.

Answer:

\(4 \sqrt [ 3 ] { 10 } + \sqrt { 10 }\)

Adding and Subtracting Radical Expressions

Often, we will have to simplify before we can identify the like radicals within the terms.

Example \(\PageIndex{5}\):

Subtract: \(\sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 }\).

Solution

At first glance, the radicals do not appear to be similar. However, after simplifying completely, we will see that we can combine them.

\(\begin{aligned} \sqrt { 32 } - \sqrt { 18 } + \sqrt { 50 } & = \sqrt { 16 } \cdot 2 - \sqrt { 9 \cdot 2 } + \sqrt { 25 \cdot 2 } \\ & = 4 \sqrt { 2 } - 3 \sqrt { 2 } + 5 \sqrt { 2 } \\ & = 6 \sqrt { 2 } \end{aligned}\)

Answer:

\(6\sqrt{2}\)

Example \(\PageIndex{6}\):

Simplify: \(\sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 }\).

Solution:

Begin by looking for perfect cube factors of each radicand.

\(\begin{aligned} \sqrt [ 3 ] { 108 } + \sqrt [ 3 ] { 24 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 81 } & = \sqrt [ 3 ] { 27 \cdot 4 } + \sqrt [ 3 ] { 8 \cdot 3 } - \sqrt [ 3 ] { 8 \cdot 4 } - \sqrt [ 3 ] { 27 \cdot 3 }\quad\color{Cerulean}{Simplify.} \\ & = 3 \sqrt [ 3 ] { 4 } + \color{Cerulean}{2 \sqrt [ 3 ] { 3 } }\color{black}{-} 2 \sqrt [ 3 ] { 4 } - \color{Cerulean}{3 \sqrt [ 3 ] { 3 }} \quad\quad\quad\quad\quad\color{Cerulean}{Combine\:like\:terms.} \\ & = \sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 } \end{aligned}\)

Answer:

\(\sqrt [ 3 ] { 4 } - \sqrt [ 3 ] { 3 }\)

Exercise \(\PageIndex{1}\)

Simplify: \(\sqrt { 20 } + \sqrt { 27 } - 3 \sqrt { 5 } - 2 \sqrt { 12 }\).

Answer

\(- \sqrt { 5 } - \sqrt { 3 }\)

www.youtube.com/v/QtaPdVybP1g

Next, we work with radical expressions involving variables. In this section, assume all radicands containing variable expressions are nonnegative.

Example \(\PageIndex{7}\):

Simplify: \(- 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x }\).

Solution

Combine like radicals.

\(\begin{aligned} - 9 \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } + 10 \sqrt [ 3 ] { 5 x } & = \color{Cerulean}{- 9 \sqrt [ 3 ] { 5 x } + 10 \sqrt [ 3 ] { 5 x } }\color{black}{-}\color{OliveGreen}{ \sqrt [ 3 ] { 2 x }} \\ & = \sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \end{aligned}\)

We cannot combine any further because the remaining radical expressions do not share the same radicand; they are not like radicals. Note: \(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x } \neq \sqrt [ 3 ] { 5 x - 2 x }\).

Answer:

\(\sqrt [ 3 ] { 5 x } - \sqrt [ 3 ] { 2 x }\)

We will often find the need to subtract a radical expression with multiple terms. If this is the case, remember to apply the distributive property before combining like terms.

Example \(\PageIndex{8}\):

Simplify: \(( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } )\).

Solution

\(\begin{aligned} ( 5 \sqrt { x } - 4 \sqrt { y } ) - ( 4 \sqrt { x } - 7 \sqrt { y } ) & = 5 \sqrt { x } - 4 \sqrt { y } - 4 \sqrt { x } + 7 \sqrt { y } \quad\color{Cerulean}{Distribute.} \\ & = 5 \sqrt { x } - 4 \sqrt { x } - 4 \sqrt { y } + 7 \sqrt { y } \\ & = \sqrt { x } + 3 \sqrt { y } \end{aligned}\)

Answer:

\(\sqrt { x } + 3 \sqrt { y }\)

Until we simplify, it is often unclear which terms involving radicals are similar. The general steps for simplifying radical expressions are outlined in the following example.

Example \(\PageIndex{9}\):

Simplify: \(5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right)\).

Solution

Step 1: Simplify the radical expression. In this case, distribute and then simplify each term that involves a radical.

\(\begin{array} { l } { 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - \left( x \sqrt [ 3 ] { 24 x } + 4 \sqrt [ 3 ] { 3 x ^ { 3 } } \right) } \\ { = 5 \sqrt [ 3 ] { 3 x ^ { 4 } } + \sqrt [ 3 ] { 24 x ^ { 3 } } - x \sqrt[3] { 24 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 \sqrt [ 3 ] { 3 \cdot x \cdot x ^ { 3 } } + \sqrt [ 3 ] { 8 \cdot 3 \cdot x ^ { 3 } } - x \sqrt [ 3 ] { 8 \cdot 3 x } - 4 \sqrt [ 3 ] { 3 x ^ { 3 } } } \\ { = 5 x \sqrt [ 3 ] { 3 x } + 2 x \sqrt [ 3 ] { 3 } - 2 x \sqrt [ 3 ] { 3 x } - 4 x \sqrt [ 3 ] { 3 } } \end{array}\)

Step 2: Combine all like radicals. Remember to add only the coefficients; the variable parts remain the same.

\(\begin{array} { l } { =\color{Cerulean}{ 5 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{+ 2 x \sqrt [ 3 ] { 3 }}\color{Cerulean}{ - 2 x \sqrt [ 3 ] { 3 x } }\color{OliveGreen}{- 4 x \sqrt [ 3 ] { 3 } } }\\ { = 3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 } } \end{array}\)

Answer: \(3 x \sqrt [ 3 ] { 3 x } - 2 x \sqrt [ 3 ] { 3 }\)

Example \(\PageIndex{10}\):

Simplify: \(2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b }\).

Solution

\(\begin{array} { l } { 2 a \sqrt { 125 a ^ { 2 } b } - a ^ { 2 } \sqrt { 80 b } + 4 \sqrt { 20 a ^ { 4 } b } } \\ { = 2 a \sqrt { 25 \cdot 5 \cdot a ^ { 2 } \cdot b } - a ^ { 2 } \sqrt { 16 \cdot 5 \cdot b } + 4 \sqrt { 4 \cdot 5 \cdot \left( a ^ { 2 } \right) ^ { 2 } b } }\quad\color{Cerulean}{Factor.} \\ { = 2 a \cdot 5 \cdot a \sqrt { 5 b } - a ^ { 2 } \cdot 4 \sqrt { 5 b } + 4 \cdot 2 \cdot a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\:\color{Cerulean}{Simplify.} \\ { = 10 a ^ { 2 } \sqrt { 5 b } - 4 a ^ { 2 } \sqrt { 5 b } + 8 a ^ { 2 } \sqrt { 5 b } } \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\color{Cerulean}{Combine\:like\:terms.} \\ { = 14 a ^ { 2 } \sqrt { 5 b } } \end{array}\)

Answer:

\(14 a ^ { 2 } \sqrt { 5 b }\)

Exercise \(\PageIndex{2}\)

\(\sqrt [ 3 ] { 2 x ^ { 6 } y } + \sqrt [ 3 ] { x y ^ { 3 } } - \left( y \sqrt [ 3 ] { 27 x } - 2 x \sqrt [ 3 ] { 2 x ^ { 3 } y } \right)\)

Answer

\(3 x ^ { 2 } \sqrt [ 3 ] { 2 y } - 2 y \sqrt [ 3 ] { x }\)

www.youtube.com/v/oYeyj7ubc-Q

note

Take careful note of the differences between products and sums within a radical. Assume both \(x\) and \(y\) are nonnegative.

\(\begin{array} { l } Products \quad \quad\quad\quad Sums\\\hline { \sqrt { x ^ { 2 } y ^ { 2 } } = x y \quad\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y } \\ { \sqrt [ 3 ] { x ^ { 3 } y ^ { 3 } } = x y } \quad\sqrt[3]{x^{3}+y^{3}} \neq x+ y \end{array}\)

The property \(\sqrt [ n ] { a \cdot b } = \sqrt [ n ] { a } \cdot \sqrt [ n ] { b }\) says that we can simplify radicals when the operation in the radicand is multiplication. There is no corresponding property for addition.

Example \(\PageIndex{11}\):

Calculate the perimeter of the triangle formed by the points \((-2,-1), (-3,6)\), and \((2,1)\).

Solution

The formula for the perimeter of a triangle is \(P = a + b + c\) where \(a, b\), and \(c\) represent the lengths of each side. Plotting the points we have,

Figure \(\PageIndex{1}\)

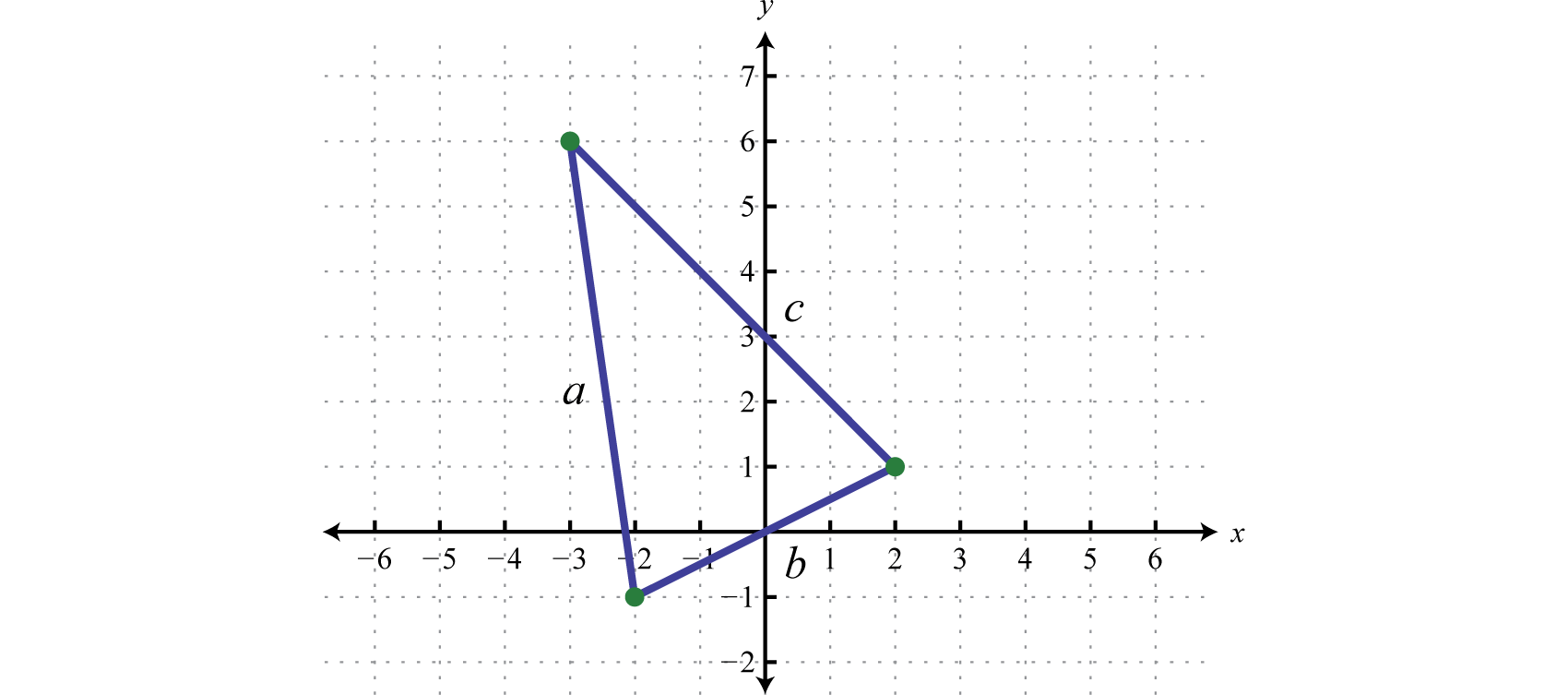
Use the distance formula to calculate the length of each side.

\(\begin{aligned} a & = \sqrt { [ - 3 - ( - 2 ) ] ^ { 2 } + [ 6 - ( - 1 ) ] ^ { 2 } } &b&= \sqrt{[2-(-2)]^{2} + [1-(-1)]^{2}} \\ & = \sqrt { ( - 3 + 2 ) ^ { 2 } + ( 6 + 1 ) ^ { 2 } } &&= \sqrt{(2+2)^{2} + (1+1)^{2}} \\ & = \sqrt { ( - 1 ) ^ { 2 } + ( 7 ) ^ { 2 } } &&=\sqrt{(4)^{2}+(2)^{2}} \\ & = \sqrt { 1 + 49 }&&= \sqrt{16+4} \\ & = \sqrt { 50 } && =\sqrt{20}\\ & = 5 \sqrt { 2 } &&= 2\sqrt{5} \end{aligned}\)

Similarly we can calculate the distance between \((−3, 6)\) and \((2,1)\) and find that \(c = 5\sqrt{2}\) units. Therefore, we can calculate the perimeter as follows:

\(\begin{aligned} P & = a + b + c \\ & = 5 \sqrt { 2 } + 2 \sqrt { 5 } + 5 \sqrt { 2 } \\ & = 10 \sqrt { 2 } + 2 \sqrt { 5 } \end{aligned}\)

Answer:

\(10 \sqrt { 2 } + 2 \sqrt { 5 }\) units

Key Takeaways

• Add and subtract terms that contain like radicals just as you do like terms. If the index and radicand are exactly the same, then the radicals are similar and can be combined. This involves adding or subtracting only the coefficients; the radical part remains the same.
• Simplify each radical completely before combining like terms.

Exercise \(\PageIndex{3}\)

Simplify

1. \(10 \sqrt { 3 } - 5 \sqrt { 3 }\)
2. \(15 \sqrt { 6 } - 8 \sqrt { 6 }\)
3. \(9 \sqrt { 3 } + 5 \sqrt { 3 }\)
4. \(12 \sqrt { 6 } + 3 \sqrt { 6 }\)
5. \(4 \sqrt { 5 } - 7 \sqrt { 5 } - 2 \sqrt { 5 }\)
6. \(3 \sqrt { 10 } - 8 \sqrt { 10 } - 2 \sqrt { 10 }\)
7. \(\sqrt { 6 } - 4 \sqrt { 6 } + 2 \sqrt { 6 }\)
8. \(5 \sqrt { 10 } - 15 \sqrt { 10 } - 2 \sqrt { 10 }\)
9. \(13 \sqrt { 7 } - 6 \sqrt { 2 } - 5 \sqrt { 7 } + 5 \sqrt { 2 }\)
10. \(10 \sqrt { 13 } - 12 \sqrt { 15 } + 5 \sqrt { 13 } - 18 \sqrt { 15 }\)
11. \(6 \sqrt { 5 } - ( 4 \sqrt { 3 } - 3 \sqrt { 5 } )\)
12. \(- 12 \sqrt { 2 } - ( 6 \sqrt { 6 } + \sqrt { 2 } )\)
13. \(( 2 \sqrt { 5 } - 3 \sqrt { 10 } ) - ( \sqrt { 10 } + 3 \sqrt { 5 } )\)
14. \(( - 8 \sqrt { 3 } + 6 \sqrt { 15 } ) - ( \sqrt { 3 } - \sqrt { 15 } )\)
15. \(4 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 6 }\)
16. \(\sqrt [ 3 ] { 10 } + 5 \sqrt [ 3 ] { 10 } - 4 \sqrt [ 3 ] { 10 }\)
17. \(( 7 \sqrt [ 3 ] { 9 } - 4 \sqrt [ 3 ] { 3 } ) - ( \sqrt [ 3 ] { 9 } - 3 \sqrt [ 3 ] { 3 } )\)
18. \(( - 8 \sqrt [ 3 ] { 5 } + \sqrt [ 3 ] { 25 } ) - ( 2 \sqrt [ 3 ] { 5 } + 6 \sqrt [ 3 ] { 25 } )\)

Answer

1. \(5 \sqrt { 3 }\)

3. \(14 \sqrt { 3 }\)

5. \(- 5 \sqrt { 5 }\)

7. \(- \sqrt { 6 }\)

9. \(8 \sqrt { 7 } - \sqrt { 2 }\)

11. \(9 \sqrt { 5 } - 4 \sqrt { 3 }\)

13. \(- \sqrt { 5 } - 4 \sqrt { 10 }\)

15. \(10 \sqrt [ 3 ] { 6 } - 3 \sqrt [ 3 ] { 5 }\)

17. \(6 \sqrt [ 3 ] { 9 } - \sqrt [ 3 ] { 3 }\)

Exercise \(\PageIndex{4}\)

Simplify. (Assume all radicands containing variable expressions are positive.)

1. \(\sqrt { 2 x } - 4 \sqrt { 2 x }\)
2. \(5 \sqrt { 3 y } - 6 \sqrt { 3 y }\)
3. \(9 \sqrt { x } + 7 \sqrt { x }\)
4. \(- 8 \sqrt { y } + 4 \sqrt { y }\)
5. \(7 x \sqrt { y } - 3 x \sqrt { y } + x \sqrt { y }\)
6. \(10 y ^ { 2 } \sqrt { x } - 12 y ^ { 2 } \sqrt { x } - 2 y ^ { 2 } \sqrt { x }\)
7. \(2 \sqrt { a b } - 5 \sqrt { a } + 6 \sqrt { a b } - 10 \sqrt { a }\)
8. \(- 3 x \sqrt { y } + 6 \sqrt { y } - 4 x \sqrt { y } - 7 \sqrt { y }\)
9. \(5 \sqrt { x y } - ( 3 \sqrt { x y } - 7 \sqrt { x y } )\)
10. \(- 8 a \sqrt { b } - ( 2 a \sqrt { b } - 4 \sqrt { a b } )\)
11. \(( 3 \sqrt { 2 x } - \sqrt { 3 x } ) - ( \sqrt { 2 x } - 7 \sqrt { 3 x } )\)
12. \(( \sqrt { y } - 4 \sqrt { 2 y } ) - ( \sqrt { y } - 5 \sqrt { 2 y } )\)
13. \(5 \sqrt [ 3 ] { x } - 12 \sqrt [ 3 ] { x }\)
14. \(- 2 \sqrt [ 3 ] { y } - 3 \sqrt [ 3 ] { y }\)
15. \(a \sqrt [ 5 ] { 3 b } + 4 a \sqrt [ 5 ] { 3 b } - a \sqrt [ 5 ] { 3 b }\)
16. \(- 8 \sqrt [ 4 ] { a b } + 3 \sqrt [ 4 ] { a b } - 2 \sqrt [ 4 ] { a b }\)
17. \(6 \sqrt { 2 a } - 4 \sqrt [ 3 ] { 2 a } + 7 \sqrt { 2 a } - \sqrt [ 3 ] { 2 a }\)
18. \(4 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a } - 9 \sqrt [ 5 ] { 3 a } + \sqrt [ 3 ] { 3 a }\)
19. \(( \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } ) - ( 2 \sqrt [ 4 ] { 4 x y } - \sqrt [ 3 ] { x y } )\)
20. \(( 5 \sqrt [ 5 ] { 6 y } - 5 \sqrt { y } ) - ( 2 \sqrt [ 6 ] { 6 y } + 3 \sqrt { y } )\)
21. \(2 x ^ { 2 } \sqrt [ 3 ] { 3 x } - \left( x ^ { 2 } \sqrt [ 3 ] { 3 x } - x \sqrt [ 3 ] { 3 x } \right)\)
22. \(5 y ^ { 3 } \sqrt { 6 y } - \left( \sqrt { 6 y } - 4 y ^ { 3 } \sqrt { 6 y } \right)\)

Answer

1. \(- 3 \sqrt { 2 x }\)

3. \(16 \sqrt { x }\)

5. \(5 x \sqrt { y }\)

7. \(8 \sqrt { a b } - 15 \sqrt { a }\)

9. \(9 \sqrt { x y }\)

11. \(2 \sqrt { 2 x } + 6 \sqrt { 3 x }\)

13. \(- 7 \sqrt [ 3 ] { x }\)

15. \(4 a \sqrt [ 5 ] { 3 b }\)

17. \(13 \sqrt { 2 a } - 5 \sqrt [ 3 ] { 2 a }\)

19. \(- \sqrt [ 4 ] { 4 x y }\)

21. \(x ^ { 2 } \sqrt [ 3 ] { 3 x } + x \sqrt [ 3 ] { 3 x }\)

Exercise \(\PageIndex{5}\)

Simplify.

1. \(\sqrt { 75 } - \sqrt { 12 }\)
2. \(\sqrt { 24 } - \sqrt { 54 }\)
3. \(\sqrt { 32 } + \sqrt { 27 } - \sqrt { 8 }\)
4. \(\sqrt { 20 } + \sqrt { 48 } - \sqrt { 45 }\)
5. \(\sqrt { 28 } - \sqrt { 27 } + \sqrt { 63 } - \sqrt { 12 }\)
6. \(\sqrt { 90 } + \sqrt { 24 } - \sqrt { 40 } - \sqrt { 54 }\)
7. \(\sqrt { 45 } - \sqrt { 80 } + \sqrt { 245 } - \sqrt { 5 }\)
8. \(\sqrt { 108 } + \sqrt { 48 } - \sqrt { 75 } - \sqrt { 3 }\)
9. \(4 \sqrt { 2 } - ( \sqrt { 27 } - \sqrt { 72 } )\)
10. \(- 3 \sqrt { 5 } - ( \sqrt { 20 } - \sqrt { 50 } )\)
11. \(\sqrt [ 3 ] { 16 } - \sqrt [ 3 ] { 54 }\)
12. \(\sqrt [ 3 ] { 81 } - \sqrt [ 3 ] { 24 }\)
13. \(\sqrt [ 3 ] { 135 } + \sqrt [ 3 ] { 40 } - \sqrt [ 3 ] { 5 }\)
14. \(\sqrt [ 3 ] { 108 } - \sqrt [ 3 ] { 32 } - \sqrt [ 3 ] { 4 }\)
15. \(2 \sqrt { 27 } - 2 \sqrt { 12 }\)
16. \(3 \sqrt { 50 } - 4 \sqrt { 32 }\)
17. \(3 \sqrt { 243 } - 2 \sqrt { 18 } - \sqrt { 48 }\)
18. \(6 \sqrt { 216 } - 2 \sqrt { 24 } - 2 \sqrt { 96 }\)
19. \(2 \sqrt { 18 } - 3 \sqrt { 75 } - 2 \sqrt { 98 } + 4 \sqrt { 48 }\)
20. \(2 \sqrt { 45 } - \sqrt { 12 } + 2 \sqrt { 20 } - \sqrt { 108 }\)
21. \(( 2 \sqrt { 363 } - 3 \sqrt { 96 } ) - ( 7 \sqrt { 12 } - 2 \sqrt { 54 } )\)
22. \(( 2 \sqrt { 288 } + 3 \sqrt { 360 } ) - ( 2 \sqrt { 72 } - 7 \sqrt { 40 } )\)
23. \(3 \sqrt [ 3 ] { 54 } + 5 \sqrt [ 3 ] { 250 } - 4 \sqrt [ 3 ] { 16 }\)
24. \(4 \sqrt [ 3 ] { 162 } - 2 \sqrt [ 3 ] { 384 } - 3 \sqrt [ 3 ] { 750 }\)

Answer

1. \(3 \sqrt { 3 }\)

3. \(2 \sqrt { 2 } + 3 \sqrt { 3 }\)

5. \(5 \sqrt { 7 } - 5 \sqrt { 3 }\)

7. \(5 \sqrt { 5 }\)

9. \(10 \sqrt { 2 } - 3 \sqrt { 3 }\)

11. \(- \sqrt [ 3 ] { 2 }\)

13. \(4 \sqrt [ 3 ] { 5 }\)

15. \(2 \sqrt { 3 }\)

17. \(23 \sqrt { 3 } - 6 \sqrt { 2 }\)

19. \(- 8 \sqrt { 2 } + \sqrt { 3 }\)

21. \(8 \sqrt { 3 } - 6 \sqrt { 6 }\)

23. \(26 \sqrt[3] { 2 }\)

Exercise \(\PageIndex{6}\)

Simplify. (Assume all radicands containing variable expressions are positive.)

1. \(\sqrt { 81 b } + \sqrt { 4 b }\)
2. \(\sqrt { 100 a } + \sqrt { a }\)
3. \(\sqrt { 9 a ^ { 2 } b } - \sqrt { 36 a ^ { 2 } b }\)
4. \(\sqrt { 50 a ^ { 2 } } - \sqrt { 18 a ^ { 2 } }\)
5. \(\sqrt { 49 x } - \sqrt { 9 y } + \sqrt { x } - \sqrt { 4 y }\)
6. \(\sqrt { 9 x } + \sqrt { 64 y } - \sqrt { 25 x } - \sqrt { y }\)
7. \(7 \sqrt { 8 x } - ( 3 \sqrt { 16 y } - 2 \sqrt { 18 x } )\)
8. \(2 \sqrt { 64 y } - ( 3 \sqrt { 32 y } - \sqrt { 81 y } )\)
9. \(2 \sqrt { 9 m ^ { 2 } n } - 5 m \sqrt { 9 n } + \sqrt { m ^ { 2 } n }\)
10. \(4 \sqrt { 18 n ^ { 2 } m } - 2 n \sqrt { 8 m } + n \sqrt { 2 m }\)
11. \(\sqrt { 4 x ^ { 2 } y } - \sqrt { 9 x y ^ { 2 } } - \sqrt { 16 x ^ { 2 } y } + \sqrt { y ^ { 2 } x }\)
12. \(\sqrt { 32 x ^ { 2 } y ^ { 2 } } + \sqrt { 12 x ^ { 2 } y } - \sqrt { 18 x ^ { 2 } y ^ { 2 } } - \sqrt { 27 x ^ { 2 } y }\)
13. \(\left( \sqrt { 9 x ^ { 2 } y } - \sqrt { 16 y } \right) - \left( \sqrt { 49 x ^ { 2 } y } - 4 \sqrt { y } \right)\)
14. \(\left( \sqrt { 72 x ^ { 2 } y ^ { 2 } } - \sqrt { 18 x ^ { 2 } y } \right) - \left( \sqrt { 50 x ^ { 2 } y ^ { 2 } } + x \sqrt { 2 y } \right)\)
15. \(\sqrt { 12 m ^ { 4 } n } - m \sqrt { 75 m ^ { 2 } n } + 2 \sqrt { 27 m ^ { 4 } n }\)
16. \(5 n \sqrt { 27 m n ^ { 2 } } + 2 \sqrt { 12 m n ^ { 4 } } - n \sqrt { 3 m n ^ { 2 } }\)
17. \(2 \sqrt { 27 a ^ { 3 } b } - a \sqrt { 48 a b } - a \sqrt { 144 a ^ { 3 } b }\)
18. \(2 \sqrt { 98 a ^ { 4 } b } - 2 a \sqrt { 162 a ^ { 2 } b } + a \sqrt { 200 b }\)
19. \(\sqrt [ 3 ] { 125 a } - \sqrt [ 3 ] { 27 a }\)
20. \(\sqrt [ 3 ] { 1000 a ^ { 2 } } - \sqrt [ 3 ] { 64 a ^ { 2 } }\)
21. \(2 x \sqrt [ 3 ] { 54 x } - 2 \sqrt [ 3 ] { 16 x ^ { 4 } } + 5 \sqrt [ 3 ] { 2 x ^ { 4 } }\)
22. \(x \sqrt [ 3 ] { 54 x ^ { 3 } } - \sqrt [ 3 ] { 250 x ^ { 6 } } + x ^ { 2 } \sqrt [ 3 ] { 2 }\)
23. \(\sqrt [ 4 ] { 16 y ^ { 2 } } + \sqrt [ 4 ] { 81 y ^ { 2 } }\)
24. \(\sqrt [ 5 ] { 32 y ^ { 4 } } - \sqrt [ 5 ] { y ^ { 4 } }\)
25. \(\sqrt [ 4 ] { 32 a ^ { 3 } } - \sqrt [ 4 ] { 162 a ^ { 3 } } + 5 \sqrt [ 4 ] { 2 a ^ { 3 } }\)
26. \(\sqrt [ 4 ] { 80 a ^ { 4 } b } + \sqrt [ 4 ] { 5 a ^ { 4 } b } - a \sqrt [ 4 ] { 5 b }\)
27. \(\sqrt [ 3 ] { 27 x ^ { 3 } } + \sqrt [ 3 ] { 8 x } - \sqrt [ 3 ] { 125 x ^ { 3 } }\)
28. \(\sqrt [ 3 ] { 24 x } - \sqrt [ 3 ] { 128 x } - \sqrt [ 3 ] { 81 x }\)
29. \(\sqrt [ 3 ] { 27 x ^ { 4 } y } - \sqrt [ 3 ] { 8 x y ^ { 3 } } + x \sqrt [ 3 ] { 64 x y } - y \sqrt [ 3 ] { x }\)
30. \(\sqrt [ 3 ] { 125 x y ^ { 3 } } + \sqrt [ 3 ] { 8 x ^ { 3 } y } - \sqrt [ 3 ] { 216 x y ^ { 3 } } + 10 x ^ { 3 } \sqrt { y }\)
31. \(\left( \sqrt [ 3 ] { 162 x ^ { 4 } y } - \sqrt [ 3 ] { 250 x ^ { 4 } y ^ { 2 } } \right) - \left( \sqrt [ 3 ] { 2 x ^ { 4 } y ^ { 2 } } - \sqrt [ 3 ] { 384 x ^ { 4 } y } \right)\)
32. \(\left( \sqrt [ 5 ] { 32 x ^ { 2 } y ^ { 6 } } - \sqrt [ 5 ] { 243 x ^ { 6 } y ^ { 2 } } \right) - \left( \sqrt [ 5 ] { x ^ { 2 } y ^ { 6 } } - x \sqrt [ 5 ] { x y ^ { 2 } } \right)\)

Answer

1. \(11 \sqrt { b }\)

3. \(- 3 a \sqrt { b }\)

5. \(8 \sqrt { x } - 5 \sqrt { y }\)

7. \(20 \sqrt { 2 x } - 12 \sqrt { y }\)

9. \(- 8 m \sqrt { n }\)

11. \(- 2 x \sqrt { y } - 2 y \sqrt { x }\)

13. \(- 4 x \sqrt { y }\)

15. \(3 m ^ { 2 } \sqrt { 3 n }\)

17. \(2 a \sqrt { 3 a b } - 12 a ^ { 2 } \sqrt { a b }\)

19. \(2 \sqrt [ 3 ] { a }\)

21. \(7 x \sqrt [ 3 ] { 2 x }\)

23. \(5 \sqrt [ 4 ] { y ^ { 2 } }\)

25. \(4 \sqrt [ 4 ] { 2 a ^ { 3 } }\)

27. \(- 2 x + 2 \sqrt [ 3 ] { x }\)

29. \(7 x \sqrt [ 3 ] { x y } - 3 y \sqrt [ 3 ] { x }\)

31. \(7 x \sqrt [ 3 ] { 6 x y } - 6 x \sqrt [ 3 ] { 2 x y ^ { 2 } }\)

Exercise \(\PageIndex{7}\)

Calculate the perimeters of the triangles formed by the following set of vertices.

1. \(\{ ( - 4 , - 5 ) , ( - 4,3 ) , ( 2,3 ) \}\)
2. \(\{ ( - 1,1 ) , ( 3,1 ) , ( 3 , - 2 ) \}\)
3. \(\{ ( - 3,1 ) , ( - 3,5 ) , ( 1,5 ) \}\)
4. \(\{ ( - 3 , - 1 ) , ( - 3,7 ) , ( 1 , - 1 ) \}\)
5. \(\{ ( 0,0 ) , ( 2,4 ) , ( - 2,6 ) \}\)
6. \(\{ ( - 5 , - 2 ) , ( - 3,0 ) , ( 1 , - 6 ) \}\)
7. A square garden that is \(10\) feet on each side is to be fenced in. In addition, the space is to be partitioned in half using a fence along its diagonal. How much fencing is needed to do this? (Round to the nearest tenth of a foot.)
8. A garden in the shape of a square has an area of \(150\) square feet. How much fencing is needed to fence it in? (Hint: The length of each side of a square is equal to the square root of the area. Round to the nearest tenth of a foot.)

Answer

1. \(24\) units

3. \(8 + 4 \sqrt { 2 }\) units

5. \(4 \sqrt { 5 } + 2 \sqrt { 10 }\) units

7. \(54.1\) feet

Exercise \(\PageIndex{8}\)

1. Choose values for \(x\) and \(y\) and use a calculator to show that \(\sqrt { x + y } \neq \sqrt { x } + \sqrt { y }\).
2. Choose values for \(x\) and \(y\) and use a calculator to show that \(\sqrt { x ^ { 2 } + y ^ { 2 } } \neq x + y\).

Answer

1. Answer may vary

Footnotes

¹⁶Radicals that share the same index and radicand.

¹⁷Term used when referring to like radicals.