5.06: Extrapolation is a Bad Idea
- Page ID
- 126412
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson 1: Extrapolation is a Bad Idea
Learning Objectives
After successful completion of this lesson, you should be able to:
1) enumerate why using extrapolation can be a bad idea.
2) show through an example why extrapolation can be a bad idea.
Description
This conversation illustrates the pitfall of using extrapolation.
(Due to certain reasons, this student wishes to remain anonymous.)
This takes place in Summer Session B – July 2001
Student: “Hey, Dr. Kaw! Look at this cool new cell phone I just got!”
Kaw: “That’s nice. It better not ring in my class or it’s mine.”
Student: “What would you think about getting stock in this company?”
Kaw: “What company is that?”
Student: “WorldCom! They’re the world’s leading global data and internet company.”
Kaw: “So?”
Student: “They’ve just closed the deal today to merge with Intermedia Communications, based right here in Tampa!”
Kaw: “Yeah, and …?”
Student: “The stock’s booming! It’s at $14.11 per share and promised to go only one way—up! We’ll be millionaires if we invest now!”
Kaw: “You might not want to assume their stock will keep rising … besides, I’m skeptical of their success. I don’t want you putting yourself in financial ‘jeopardy!’ over some silly extrapolation. Take a look at these NASDAQ composite numbers (Table \(\PageIndex{1.1}\)).”
Student: “That’s only up to two years ago …”
Kaw: “That’s right. Looking at this data, don’t you think you should’ve invested back then?”
Student: “Well, didn’t the composite drop after that?”
Kaw: “Right again, but look what you would’ve hoped for if you had depended on that trend continuing (Figure 1).”
Student: “So you’re saying that …?”
Kaw: “You should seldom depend on extrapolation as a source of approximation! Just take a look at how wrong you would have been (Table 2).”
| End of year | NASDAQ |
|---|---|
| \(1\) | \(751.96\) |
| \(2\) | \(1052.13\) |
| \(3\) | \(1291.03\) |
| \(4\) | \(1570.35\) |
| \(5\) | \(2192.69\) |
| \(6\) | \(4069.31\) |
Note: The range of years in Table 1 are actually between 1994 (Year 1) and 1999 (Year 9). Numbers start from 1 to avoid round-off errors and near singularities in matrix calculations.
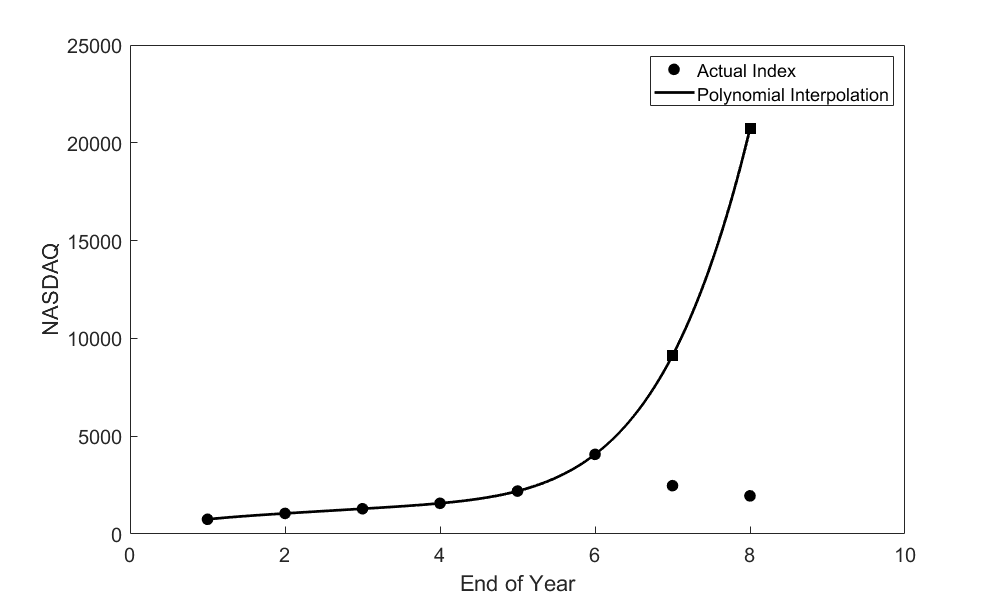
| End of Year | Actual | Fifth order polynomial interpolation | Absolute relative true error |
|---|---|---|---|
| \(2000\) | \(2471\) | \(9128\) | \(269.47 \%\) |
| \(2001\) | \(1950\) | \(20720\) | \(962.36 \%\) |
Student: “Now wait a sec! I wouldn’t have been quite that wrong. What if I had used cubic splines instead of a fifth-order interpolant?”
Kaw: “Let’s find out.”
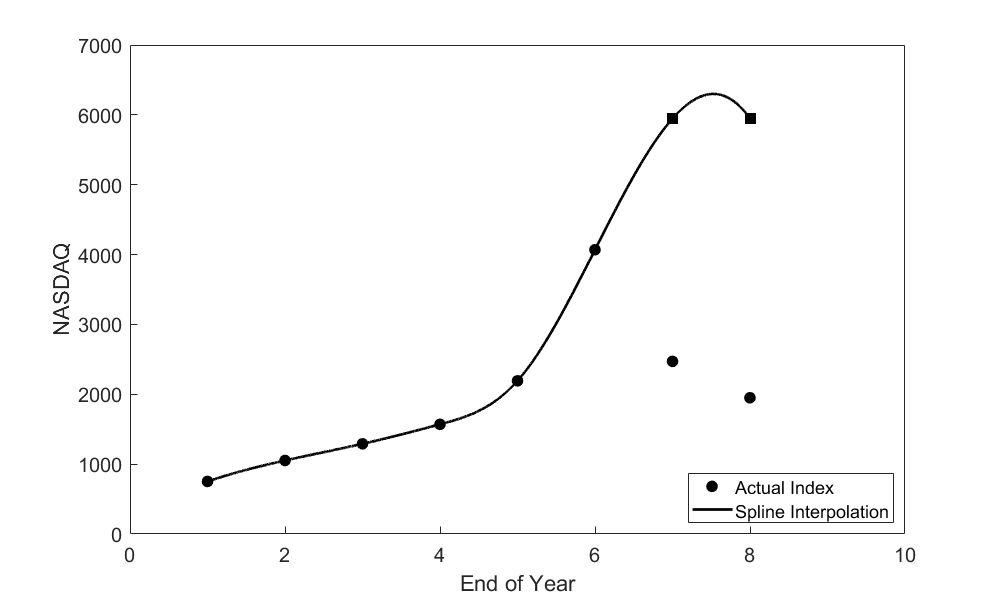
| End of Year | Actual | Cubic spline interpolation | Absolute relative true error |
|---|---|---|---|
| \(2000\) | \(2471\) | \(5945.9\) | \(140.63 \%\) |
| \(2001\) | \(1950\) | \(5947.4\) | \(204.99 \%\) |
Student: “There you go. That didn’t take so long (Figure \(\PageIndex{1.2}\) and Table \(\PageIndex{1.3}\)).”
Kaw: “Well, let’s think about what this data means. If you had gone ahead and invested, thinking your projected yield would follow the spline, you would have only been 205% (Table \(\PageIndex{1.3}\)) wrong, as opposed to being 962% (Table \(\PageIndex{1.2}\)) wrong by following the polynomial. That’s not so bad, is it?”
Student: “Okay, you’ve got a point. Maybe I’ll hold off on being an investor and just use the cell phone.”
Kaw: “You’ve got a point, too—you’re brighter than you look … that is, if you turn off the phone before coming to class.”
* * * * *
<One year later … July 2002>
Student: “Hey, Dr. Kaw! Whatcha got for me today?”
Kaw: “The Computational Methods students just took their interpolation test today, so here you go. <hands stack of tests to student> Time to grade them!”
Student: <Grunt!> “That’s a lot of paper! Boy, interpolation … learned that a while ago.”
Kaw: “You haven’t forgotten my lesson to you about not extrapolating, have you?”
Student: “Of course not! Haven’t you seen the news? WorldCom just closed down 93% from 83¢ on June 25 to 6¢ per share! They’ve had to recalculate their earnings, so your skepticism really must’ve spread. Did you have an “in” on what was going on?”
Kaw: “Oh, of course not. I’m just an ignorant numerical methods professor.”