1.3: 2D Limits
- Page ID
- 597
Topology Terminology
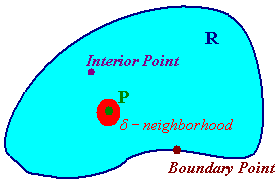
Let \(P\) be a point in the plane then a d-neighborhood (ball) of \(P\) is the set of points that are less than \(d\) units away from \(P\). If \(R\) is a region, then a point \(P\) is called an interior point of \(R\) if there is a d-neighborhood totally contained in \(R\). If every point of \(R\) is an interior point of \(R\) then \(R\) is called open. A point \(P\) is called a boundary point of \(R\) if every d-neighborhood of \(R\) contains both points in \(R\) and not in \(R\). \(R\) is called closed if it contains all of its boundary points.
Definition: Two-Dimensional Limits
Let \(f(x,y)\) be a function defined near the point \(P\), then
\[ \lim_{x \rightarrow P} f(x,y)= L\]
if there is a \(d\) such that \(f(x,y)\) is close to \(L\) for all points (except possibly \(P\)) in the d - neighborhood of \(P\).
Equivalently, the limit is \(L\) if for all paths that lead to \(P\), the function also tends towards \(P\). (Recall that for the one variable case we needed to check only the path from the left and from the right.) To show that a limit does not exist at a point, it is necessary to demonstration that two paths that both lead to \(P\) such that \(f(x,y)\) tends towards different values.
Techniques For Finding Limits
Example \(\PageIndex{1}\)
Show that
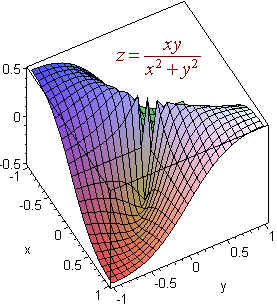
\[ \lim_{(x,y) \rightarrow (0,0)} \dfrac{xy}{x^2+y^2}\]
does not exist.
Solution
First select the path along the x-axis. On this path
\[y = 0 \]
so the function becomes:
\[ f(x,0)=\dfrac{0}{x^2} = 0.\]
Now choose the path along the y = x line:
\[ f(0,y)= \dfrac{x^2}{2x^2} = \dfrac{1}{2}.\]
Hence the function tends towards two different values for different paths. We can conclude that the limit does not exist. The graph is pictured below.
Example \(\PageIndex{2}\)
Find
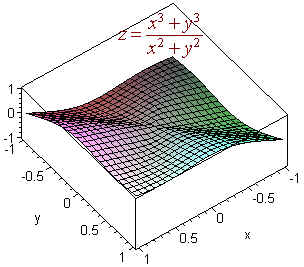
\[ \lim_{(x,y) \rightarrow (0,0)} \dfrac{x^3+y^3}{x^2+y^2}.\]
Solution
We could try the paths from the last example, but both paths give a value of 0 for the limit. Hence we suspect that the limit exists. We convert to polar coordinates and take the limit as \(r\) approaches 0:
We have
\[ f(r,q) =\dfrac{r^3\cos^3q + r^3\sin^3q}{ r^2} = r\cos^3q + r\sin^3q \]
as \(r\) approaches 0, the function also approaches 0 no matter what \(q\) is. Hence the limit is 0. Below is the graph of this function.
Exercises
Find the limit if it exists
- \( \lim_{(x,y) \rightarrow (0,1)} \dfrac{xy-x}{x^2+y^2-2y+1}\)
- \( \lim_{(x,y) \rightarrow (0,1)} \dfrac{4x^2y^2}{x^4+y^4}\)
Continuity
We make the following definition for continuity.
Definition: Continuity
A function of several variables is continuous at a point \(P\) if the limit exists at \(P\) and the function defined at \(P\) is equal to this limit.
As with functions of one variable, polynomials are continuous, sums, products, and compositions of continuous functions are continuous. Quotients of continuous functions are continuous. A function is continuous if it is continuous at every point.
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


