4.3: Subspaces
- Page ID
- 316
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
As mentioned in the last section, there are countless examples of vector spaces. One particularly important source of new vector spaces comes from looking at subsets of a set that is already known to be a vector space.
Definition 4.3.1. Let \(V\) be a vector space over \( \mathbb{F}\), and let \( U\) be a subset of \(V\) . Then we call \(U\) a subspace of \(V\) if \(U\) is a vector space over \(\mathbb{F}\) under the same operations that make \(V\) into a vector space over \(\mathbb{F}\).
To check that a subset \(U\) of \(V\) is a subspace, it suffices to check only a few of the conditions of a vector space.
Lemma 4.3.2. Let \( U \subset V \) be a subset of a vector space \(V\) over \(F\). Then \(U\) is a subspace of \(V\) if and only if the following three conditions hold.
- additive identity: \( 0 \in U \);
- closure under addition: \(u, v \in U \Rightarrow u + v \in U\);
- closure under scalar multiplication: \( a \in \mathbb{F}, ~u \in U \implies au \in U \).
Proof. Condition 1 implies that the additive identity exists. Condition 2 implies that vector addition is well-defined and, Condition 3 ensures that scalar multiplication is well-defined. All other conditions for a vector space are inherited from V since addition and scalar multiplication for elements in \(U\) are the same when viewed as elements in either \(U\) or \(V\) .
Remark 4.3.3. Note that if we require \(U \in V\) to be a nonempty subset of \(V\), then condition 1 of Lemma 4.3.2 already follows from condition 3 since \(0u = 0 \rm{~for~} u \in U\).
Example 4.3.4. In every vector space \(V\) , the subsets \({0}\) and \(V\) are easily verified to be subspaces. We call these the trivial subspaces of \(V\) .
Example 4.3.5. \({(x_1 , 0) | x_1 \in R} \) is a subspace of R2 .
Example 4.3.6. \( U = { (x_1 , x_2 , x_3) \in \mathbb{F}^3 | x_1 + 2x_2 = 0 } \) is a subspace of \(\mathbb{F}^3\) . To see this, we need to check the three conditions of Lemma 4.3.2.
The zero vector \((0, 0, 0) \in \mathbb{F}^3\) is in \(U\) since it satisfies the condition \(x_1 + 2x_2 = 0\). To show that \(U\) is closed under addition, take two vectors \(v = (v_1 , v_2 , v_3 ) \) and \(u = (u_1 , u_2, u_3 )\). Then, by the definition of \(U\), we have \(v_1 + 2v_2 = 0\) and\( u_1 + 2u_2 = 0\). Adding these two equations, it is not hard to see that the vector
\[ v + u = (v_1 + u_1, v_2 + u_2 , v_3 + u_3 ) \rm{~satisfies~} (v_1 + u_1 ) + 2(v_2 + u_2 ) = 0. \]
Hence \(v + u \in U\). Similarly, to show closure under scalar multiplication, take \(u = (u_1 , u_2, u_3 ) \in U\) and \(a \in \mathbb{F}\). Then \(au = (au_1 , au_2 , au-3 )\) satisfies the
equation \(au_1 + 2au_2 = a(u_1 + 2u_2 ) = 0\), and so \(au \in U\).
Example 4.3.7. \(U = {p \in \mathbb{F}[z] | p(3) = 0}\) is a subspace of \(\mathbb{F}[z]\). Again, to check this, we need to verify the three conditions of Lemma 4.3.2.
Certainly the zero polynomial \( p(z) = 0z^n + 0z^{n-1}+ \ldots + 0z + 0\) is in \(U\) since \(p(z\)) evaluated at 3 is 0. If \(f(z)\), \(g(z)\) \in U\), then \(f (3) = g(3) = 0\) so that \((f + g)(3) = f (3) + g(3) = 0 + 0 = 0\). Hence \(f + g \in U\), which proves closure under addition. Similarly, \((af )(3) = af (3) = a0 = 0\) for any \(a \in F\), which proves closure under scalar multiplication.
Example 4.3.8. As in Example 4.1.6, let \(D \subset \mathbb{R}\) be a subset of \(\mathbb{R}\), and let \(\cal{C}^{\infty}(D)\) denote the set of all smooth (a.k.a. continuously differentiable) functions with domain \(D\) and codomain \(\mathbb{R}\). Then, under the same operations of pointwise addition and scalar multiplication, one can show that \(\cal{C}^{\infty}(D)\) is a subspace of \(\cal{C}(D)\).
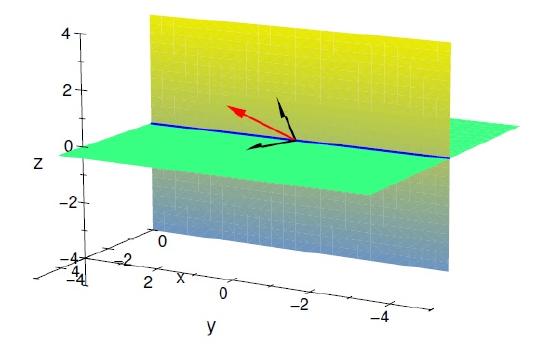
Figure 4.3.1: The intersection \(U \cap U^\prime\) of two subspaces is a subspace.
Example 4.3.9. The subspaces of \(\mathbb{R}^2\) consist of \({0}\), all lines through the origin, and \(\mathbb{R}^2\) itself. The subspaces of \(\mathbb{R}^3\) are {0}, all lines through the origin, all planes through the origin, and \(\mathbb{R}^3\). In fact, these exhaust all subspaces of \(\mathbb{R}^2\) and \(\mathbb{R}^3\) , respectively. To prove this, we will need further tools such as the notion of bases and dimensions to be discussed soon. In particular, this shows that lines and planes that do not pass through the origin are not subspaces (which is not so hard to show!).
Note that if \(U\) and \(U^\prime\) are subspaces of \(V\) , then their intersection \(U \cap U^\prime\) is also a subspace (see Proof-writing Exercise 2 and Figure 4.3.1). However, the union of two subspaces is not necessarily a subspace. Think, for example, of the union of two lines in \(\mathbb{R}^2\) , as in Figure 4.4.1 in the next chapter.
Contributors
- Isaiah Lankham, Mathematics Department at UC Davis
- Bruno Nachtergaele, Mathematics Department at UC Davis
- Anne Schilling, Mathematics Department at UC Davis
Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.


