4.4: Sums and direct sum

Last updated
Save as PDF

Page ID: 317

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Throughout this section, $V$ is a vector space over $\mathbb{F}$, and $U_1 , U_2 \subset V$ denote subspaces.

Definition 4.4.1: (subspace) sum

Let $U_1 , U_2 \subset V$ be subspaces of $V$ . Deﬁne the (subspace) sum of $U_1$

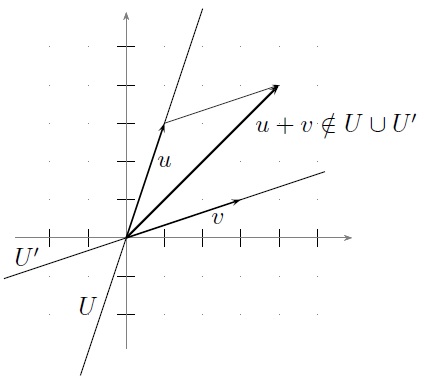
$figure 4.4.1 - Copy.jpg$

Figure 4.4.1: The union $U \cup U^\prime$ of two subspaces is not necessarily a subspace.

and $U_2$ to be the set

\[ U_1 + U_2 = \{u_1 + u_2 | u_1 \in U_1 , u_2 \in U_2 \}. \tag{4.4.1}\]

Check as an exercise that $U_1 + U_2$ is a subspace of $V$ . In fact, $U_1 + U_2$ is the smallest subspace of $V$ that contains both $U_1$ and $U_2$ .

Example 4.4.2. Let

\[ U_1 = \{(x, 0, 0) \in \mathbb{F}^3 | x \in \mathbb{F}\}, \\ U_2 = \{(0, y, 0) \in \mathbb{F}^3 | y \in \mathbb{F}\}.\]

Then

\[U_1 + U_2 = \{(x, y, 0) \in \mathbb{F}^3 | x, y \in \mathbb{F}\}. \tag{4.4.2}\]

If, alternatively, $U_2 = \{(y, y, 0) \in \mathbb{F}^3 | y \in \mathbb{F}\}$, then Equation (4.4.2) still holds.

If $U = U_1 +U_2$ , then, for any $u \in U$, there exist $u_1 \in U_1$ and $u_2 \in U_2$ such that $u = u_1 +u_2.$

If it so happens that $u$ can be uniquely written as $u_1 + u_2$ , then $U$ is called the direct sum of $U_1$ and $U_2.$

Definition 4.4.3: Direct Sum

Suppose every $u \in U$ can be uniquely written as $u = u_1 + u_2$ for $ u_1 \in U_1$ and $u_2 \in U_2$ . Then we use

\[U = U_1 \oplus U_2\]

to denote the direct sum of $U_1$ and $U_2.$

Example 4.4.4. Let
\[U_1 = \{(x, y, 0) \in \mathbb{R}^3 | x, y \in \mathbb{R}\}, \\
U_2 = \{(0, 0, z) \in \mathbb{R}^3 | z \in \mathbb{R}\}.\]
Then $\mathbb{R}^3 = U_1 \oplus U_2$. However, if instead
\[U_2 = \{(0, w, z) | w, z \in \mathbb{R}\},\]
then $\mathbb{R}^3 = U_1 + U_2$ but is not the direct sum of $U_1$ and $U_2$ .
Example 4.4.5. Let
\[U_1 = \{p \in \mathbb{F}[z] | p(z) = a_0 + a_2 z^2 + \cdots + a_{2m}z^{2m} \}, \\
U_2 = \{p \in \mathbb{F}[z] | p(z) = a_1z + a_3z^3 + \cdots + a_{2m+1}z^{2m+1} \}.\]
Then $\mathbb{F}[z] = U_1 \oplus U_2.$

Proposition 4.4.6. Let $U_1 , U_2 \subset V$ be subspaces. Then $V = U_1 \oplus U_2$ if and only if the following two conditions hold:

$V = U_1 + U_2;$
If $0 = u_1 + u_2$ with $u_1 \in U_1$ and $u_2 \in U_2$ , then $u_1 = u_2 = 0.$

Proof.
$(“\Rightarrow”)$ Suppose $V = U_1 \oplus U_2$. Then Condition 1 holds by deﬁnition. Certainly $0 = 0 + 0$, and, since by uniqueness this is the only way to write $0 \in V$ , we have $u_1 = u_2 = 0$.

$(“\Leftarrow”)$ Suppose Conditions 1 and 2 hold. By Condition 1, we have that, for all $v \in V$ , there exist $u_1 \in U_1$ and $u_2 \in U_2$ such that $v = u_1 + u_2$ . Suppose $v = w_1 + w_2$ with $w_1 \in U_1$ and $w_2 \in U_2$ . Subtracting the two equations, we obtain

\[0 = (u_1 − w_1 ) + (u_2 − w_2 ),\]

where $u_1 − w_1 \in U_1$ and $u_2 − w_2 \in U_2$. By Condition 2, this implies $u_1 − w_1 = 0$ and $u_2 − w_2 = 0$, or equivalently $u_1 = w_1$ and $u_2 = w_2$ , as desired.

Proposition 4.4.7. Let $U_1 , U_2 \subset V$ be subspaces. Then $V = U_1 \oplus U_2$ if and only if the following two conditions hold:

$V = U_1 + U_2;$
$U_1 \cap U_2 = \{0\}.$

Proof.
$(“\Rightarrow”)$ Suppose $V = U_1 \oplus U_2$. Then Condition 1 holds by deﬁnition. If $u \in U_1 \cap U_2$ , then $0 = u + (−u)$ with $u \in U_1$ and $−u \in U_2$ (why?). By Proposition 4.4.6, we have $u = 0$ and $−u = 0$ so that $U_1 \cap U_2 = \{0\}.$

$(“\Leftarrow”)$ Suppose Conditions 1 and 2 hold. To prove that $V = U_1 \oplus U_2$ holds, suppose that

\[0 = u_1 + u_2, \rm{~where~} u_1 \in U_1 \rm{~and~} u_2 \in U_2. \tag{4.3}\]

By Proposition 4.4.6, it suﬃces to show that $u_1 = u_2 = 0$. Equation (4.3) implies that $u_1 = −u_2 \in U_2$. Hence $u_1 \in U_1 \cap U_2$, which in turn implies that $u_1 = 0$. It then follows that $u_2 = 0$ as well.

Everything in this section can be generalized to m subspaces $U_1 , U_2 , \ldots U_m,$ with the notable exception of Proposition 4.4.7. To see, this consider the following example.

Example 4.4.8. Let

\[U_1 = \{(x, y, 0) \in \mathbb{F}^3 | x, y \in \mathbb{F}\}, \\
U_2 = \{(0, 0, z) \in \mathbb{F}^3 | z \in \mathbb{F}\}, \\
U_3 = \{(0, y, y) \in \mathbb{F}^3 | y \in \mathbb{F}\}.\]

Then certainly $\mathbb{F}^3 = U_1 + U_2 + U_3$ , but $\mathbb{F}^3 \neq U_1 \oplus U_2 \oplus U_3$ since, for example,

\[(0, 0, 0) = (0, 1, 0) + (0, 0, 1) + (0, −1, −1).\]

But $U_1 \cap U_2 = U_1 \cap U_3 = U_2 \cap U_3 = \{0\}$ so that the analog of Proposition 4.4.7 does not hold.

Contributors

Both hardbound and softbound versions of this textbook are available online at WorldScientific.com.

Search

Text Color

Text Size

Margin Size

Font Type