10.3: Areas in Polar Coordinates
( \newcommand{\kernel}{\mathrm{null}\,}\)
We can use the equation of a curve in polar coordinates to compute some areas bounded by such curves. The basic approach is the same as with any application of integration: find an approximation that approaches the true value. For areas in rectangular coordinates, we approximated the region using rectangles; in polar coordinates, we use sectors of circles, as depicted in 10.3.1. Recall that the area of a sector of a circle is αr2/2, where α is the angle subtended by the sector. If the curve is given by r=f(θ), and the angle subtended by a small sector is Δθ, the area is (Δθ)(f(θ))2/2. Thus we approximate the total area as
n−1∑i=012f(θi)2Δθ.
In the limit this becomes
∫ba12f(θ)2dθ.
We find the area inside the cardioid r=1+cosθ.

Figure 10.3.1: Approximating area by sectors of circles.
Solution
∫2π012(1+cosθ)2dθ=12∫2π01+2cosθ+cos2θdθ=12(θ+2sinθ+θ2+sin2θ4)|2π0=3π2.
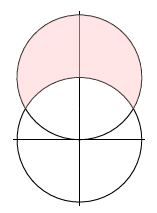
We find the area between the circles r=2 and r=4sinθ, as shown in 10.3.2.
Solution
The two curves intersect where 2=4sinθ, or sinθ=1/2, so θ=π/6 or 5π/6. The area we want is then 12∫5π/6π/616sin2θ−4dθ=43π+2√3.
This example makes the process appear more straightforward than it is. Because points have many different representations in polar coordinates, it is not always so easy to identify points of intersection.
We find the shaded area in the first graph of 10.3.3 as the difference of the other two shaded areas. The cardioid is r=1+sinθ and the circle is r=3sinθ.
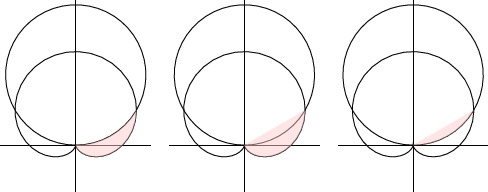
Figure 10.3.3: An area between curves.
Solution
We attempt to find points of intersection:
1+sinθ=3sinθ1=2sinθ1/2=sinθ.
This has solutions θ=π/6 and 5π/6; π/6 corresponds to the intersection in the first quadrant that we need. Note that no solution of this equation corresponds to the intersection point at the origin, but fortunately that one is obvious. The cardioid goes through the origin when θ=−π/2; the circle goes through the origin at multiples of π, starting with 0.
Now the larger region has area
12∫π/6−π/2(1+sinθ)2dθ=π2−916√3
and the smaller has area
12∫π/60(3sinθ)2dθ=3π8−916√3 so the area we seek is π/8.
Contributors
Integrated by Justin Marshall.


