5.2: Dihedral Groups

Last updated
Save as PDF

Page ID: 81061

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Another special type of permutation group is the dihedral group. Recall the symmetry group of an equilateral triangle in Chapter 3. Such groups consist of the rigid motions of a regular $n$-sided polygon or $n$-gon. For $n = 3, 4, \ldots\text{,}$ we define the nth dihedral group to be the group of rigid motions of a regular $n$-gon. We will denote this group by $D_n\text{.}$ We can number the vertices of a regular $n$-gon by $1, 2, \ldots, n$ (Figure 5.19). Notice that there are exactly $n$ choices to replace the first vertex. If we replace the first vertex by $k\text{,}$ then the second vertex must be replaced either by vertex $k+1$ or by vertex $k-1\text{;}$ hence, there are $2n$ possible rigid motions of the $n$-gon. We summarize these results in the following theorem.

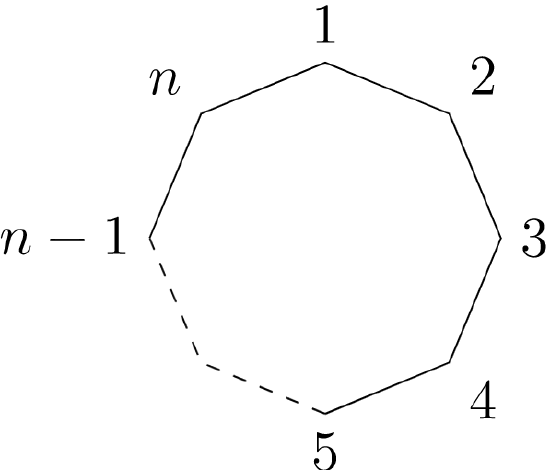
$clipboard_e2d7020c020fdd9be4f703f0a95d9e097.png$

$Figure \text { } 5.19.$ A regular $n$-gon

Theorem $5.20$

The dihedral group, $D_n\text{,}$ is a subgroup of $S_n$ of order \(2n\text{.}\

Theorem $5.21$

The group $D_n\text{,}$ $n \geq 3\text{,}$ consists of all products of the two elements $r$ and $s\text{,}$ satisfying the relations

\begin{align*} r^n & = 1\\ s^2 & = 1\\ srs & = r^{-1}\text{.} \end{align*}

Proof

The possible motions of a regular $n$-gon are either reflections or rotations (Figure 5.22). There are exactly $n$ possible rotations:

\[ \identity, \frac{360^{\circ} }{n}, 2 \cdot \frac{360^{\circ} }{n}, \ldots, (n-1) \cdot \frac{360^{\circ} }{n}\text{.} \nonumber \]

We will denote the rotation $360^{\circ} /n$ by $r\text{.}$ The rotation $r$ generates all of the other rotations. That is,

\[ r^k = k \cdot \frac{360^{\circ} }{n}\text{.} \nonumber \]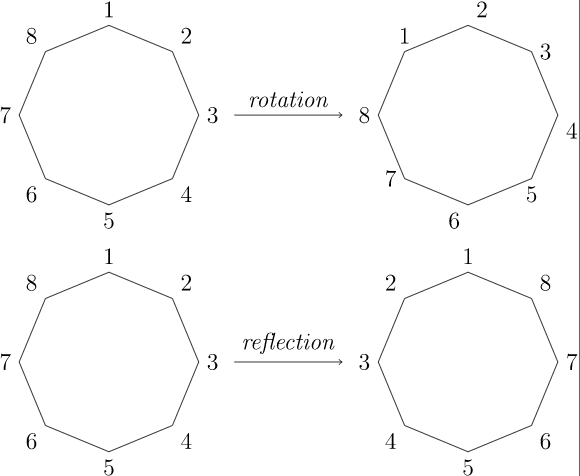

$clipboard_eb5eeaf95647d62c1e9b6083ab46e3f5e.png$

$Figure \text { } 5.22.$ Rotations and reflections of a regular $n$-gon

Label the $n$ reflections $s_1, s_2, \ldots, s_n\text{,}$ where $s_k$ is the reflection that leaves vertex $k$ fixed. There are two cases of reflections, depending on whether $n$ is even or odd. If there are an even number of vertices, then two vertices are left fixed by a reflection, and $s_1 = s_{n/2 + 1}, s_2 = s_{n/2 + 2}, \ldots, s_{n/2} = s_n\text{.}$ If there are an odd number of vertices, then only a single vertex is left fixed by a reflection and $s_1, s_2, \ldots, s_n$ are distinct (Figure 5.23). In either case, the order of each $s_k$ is two. Let $s = s_1\text{.}$ Then $s^2 = 1$ and $r^n = 1\text{.}$ Since any rigid motion $t$ of the $n$-gon replaces the first vertex by the vertex $k\text{,}$ the second vertex must be replaced by either $k+1$ or by $k-1\text{.}$ If the second vertex is replaced by $k+1\text{,}$ then $t = r^k\text{.}$ If the second vertex is replaced by $k-1\text{,}$ then $t = r^k s\text{.}$² Hence, $r$ and $s$ generate $D_n\text{.}$ That is, $D_n$ consists of all finite products of $r$ and $s\text{,}$

\[ D_n = \{1, r, r^2, \ldots, r^{n-1}, s, rs, r^2 s, \ldots, r^{n-1} s\}\text{.} \nonumber \]

We will leave the proof that $srs = r^{-1}$ as an exercise.

Since we are in an abstract group, we will adopt the convention that group elements are multiplied left to right.

$clipboard_eab994bc75d9f11b192c216cc529ea9f7.png$

$Figure \text { } 5.23.$ Types of reflections of a regular $n$-gon