19.5: Exercises

Last updated
Save as PDF

Page ID: 81193

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1

Draw the lattice diagram for the power set of $X = \{ a, b, c, d \}$ with the set inclusion relation, $\subset\text{.}$

2

Draw the diagram for the set of positive integers that are divisors of $30\text{.}$ Is this poset a Boolean algebra?

3

Draw a diagram of the lattice of subgroups of ${\mathbb Z}_{12}\text{.}$

4

Let $B$ be the set of positive integers that are divisors of $210\text{.}$ Define an order on $B$ by $a \preceq b$ if $a \mid b\text{.}$ Prove that $B$ is a Boolean algebra. Find a set $X$ such that $B$ is isomorphic to ${\mathcal P}(X)\text{.}$

5

Prove or disprove: ${\mathbb Z}$ is a poset under the relation $a \preceq b$ if $a \mid b\text{.}$

6

Draw the switching circuit for each of the following Boolean expressions.

$\displaystyle (a \vee b \vee a') \wedge a$
$\displaystyle (a \vee b)' \wedge (a \vee b)$
$\displaystyle a \vee (a \wedge b)$
$\displaystyle (c \vee a \vee b) \wedge c' \wedge (a \vee b)'$

7

Draw a circuit that will be closed exactly when only one of three switches $a\text{,}$ $b\text{,}$ and $c$ are closed.

8

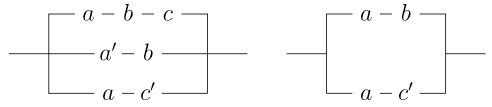
Prove or disprove that the two circuits shown are equivalent.

$clipboard_e5662dbc2f7ce018ed67a8d7fd8774ac7.png$

9

Let $X$ be a finite set containing $n$ elements. Prove that $|{\cal P}(X)| = 2^n\text{.}$ Conclude that the order of any finite Boolean algebra must be $2^n$ for some $n \in {\mathbb N}\text{.}$

10

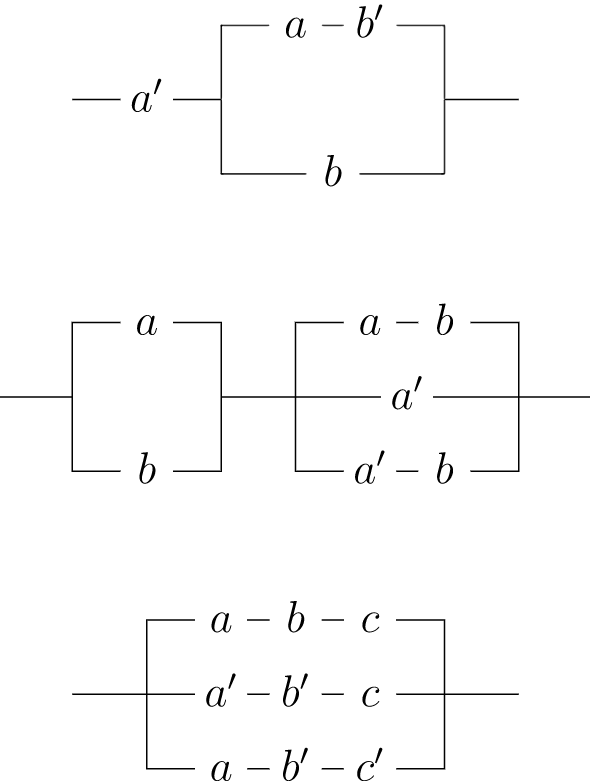
For each of the following circuits, write a Boolean expression. If the circuit can be replaced by one with fewer switches, give the Boolean expression and draw a diagram for the new circuit.

$clipboard_e71296a28342c24abfd0d3d8babc75aa2.png$

11

Prove or disprove: The set of all nonzero integers is a lattice, where $a \preceq b$ is defined by $a \mid b\text{.}$

12

Let $L$ be a nonempty set with two binary operations $\vee$ and $\wedge$ satisfying the commutative, associative, idempotent, and absorption laws. We can define a partial order on $L\text{,}$ as in Theorem $19.14$, by $a \preceq b$ if $a \vee b = b\text{.}$ Prove that the greatest lower bound of $a$ and $b$ is $a \wedge b\text{.}$

13

Let $G$ be a group and $X$ be the set of subgroups of $G$ ordered by set-theoretic inclusion. If $H$ and $K$ are subgroups of $G\text{,}$ show that the least upper bound of $H$ and $K$ is the subgroup generated by $H \cup K\text{.}$

14

Let $R$ be a ring and suppose that $X$ is the set of ideals of $R\text{.}$ Show that $X$ is a poset ordered by set-theoretic inclusion, $\subset\text{.}$ Define the meet of two ideals $I$ and $J$ in $X$ by $I \cap J$ and the join of $I$ and $J$ by $I + J\text{.}$ Prove that the set of ideals of $R$ is a lattice under these operations.

15

Let $B$ be a Boolean algebra. Prove each of the following identities.

$a \vee I = I$ and $a \wedge O = O$ for all $a \in B\text{.}$
If $a \vee b = I$ and $a \wedge b = O\text{,}$ then $b = a'\text{.}$
$(a')'=a$ for all $a \in B\text{.}$
$I' = O$ and $O' = I\text{.}$
$(a \vee b)' = a' \wedge b'$ and $(a \wedge b)' = a' \vee b'$ (De Morgan's laws).

16

By drawing the appropriate diagrams, complete the proof of Theorem $19.30$ to show that the switching functions form a Boolean algebra.

17

Let $B$ be a Boolean algebra. Define binary operations $+$ and $\cdot$ on $B$ by

\begin{align*} a + b & = (a \wedge b') \vee (a' \wedge b)\\ a \cdot b & = a \wedge b\text{.} \end{align*}

Prove that $B$ is a commutative ring under these operations satisfying $a^2 = a$ for all $a \in B\text{.}$

18

Let $X$ be a poset such that for every $a$ and $b$ in $X\text{,}$ either $a \preceq b$ or $b \preceq a\text{.}$ Then $X$ is said to be a totally ordered set.

Is $a \mid b$ a total order on ${\mathbb N}\text{?}$
Prove that ${\mathbb N}\text{,}$ ${\mathbb Z}\text{,}$ ${\mathbb Q}\text{,}$ and ${\mathbb R}$ are totally ordered sets under the usual ordering $\leq\text{.}$

19

Let $X$ and $Y$ be posets. A map $\phi : X \rightarrow Y$ is order-preserving if $a \preceq b$ implies that $\phi(a) \preceq \phi(b)\text{.}$ Let $L$ and $M$ be lattices. A map $\psi: L \rightarrow M$ is a lattice homomorphism if $\psi( a \vee b ) = \psi(a) \vee \psi(b)$ and $\psi( a \wedge b ) = \psi(a) \wedge \psi(b)\text{.}$ Show that every lattice homomorphism is order-preserving, but that it is not the case that every order-preserving homomorphism is a lattice homomorphism.

20

Let $B$ be a Boolean algebra. Prove that $a = b$ if and only if $(a \wedge b') \vee ( a' \wedge b) = O$ for $a, b \in B\text{.}$

21

Let $B$ be a Boolean algebra. Prove that $a = O$ if and only if $(a \wedge b') \vee ( a' \wedge b) = b$ for all $b \in B\text{.}$

22

Let $L$ and $M$ be lattices. Define an order relation on $L \times M$ by $( a, b) \preceq (c, d)$ if $a \preceq c$ and $b \preceq d\text{.}$ Show that $L \times M$ is a lattice under this partial order.