21.2: Splitting Fields

Let \(F\) be a field and \(p(x)\) be a nonconstant polynomial in \(F[x]\text{.}\) We already know that we can find a field extension of \(F\) that contains a root of \(p(x)\text{.}\) However, we would like to know whether an extension \(E\) of \(F\) containing all of the roots of \(p(x)\) exists. In other words, can we find a field extension of \(F\) such that \(p(x)\) factors into a product of linear polynomials? What is the “smallest” extension containing all the roots of \(p(x)\text{?}\)

Let \(F\) be a field and \(p(x) = a_0 + a_1 x + \cdots + a_n x^n\) be a nonconstant polynomial in \(F[x]\text{.}\) An extension field \(E\) of \(F\) is a splitting field of \(p(x)\) if there exist elements \(\alpha_1, \ldots, \alpha_n\) in \(E\) such that \(E = F( \alpha_1, \ldots, \alpha_n )\) and

\[ p(x) = ( x - \alpha_1 )(x - \alpha_2) \cdots (x - \alpha_n)\text{.} \nonumber \]

A polynomial \(p(x) \in F[x]\) splits in \(E\) if it is the product of linear factors in \(E[x]\text{.}\)

Example \(21.29\).

Let \(p(x) = x^4 + 2x^2 - 8\) be in \({\mathbb Q}[x]\text{.}\) Then

Solution

\(p(x)\) has irreducible factors \(x^2 -2\) and \(x^2 + 4\text{.}\) Therefore, the field \({\mathbb Q}( \sqrt{2}, i )\) is a splitting field for \(p(x)\text{.}\)

Example \(21.30\).

Let \(p(x) = x^3 - 3\) be in \({\mathbb Q}[x]\text{.}\) Then \(p(x)\) has a root in the field \({\mathbb Q}( \sqrt[3]{3}\, )\text{.}\)

Solution

However, this field is not a splitting field for \(p(x)\) since the complex cube roots of 3,

\[ \frac{ -\sqrt[3]{3} \pm (\sqrt[6]{3}\, )^5 i }{2}\text{,} \nonumber \]

are not in \({\mathbb Q}( \sqrt[3]{3}\, )\text{.}\)

Theorem \(21.31\).

Let \(p(x) \in F[x]\) be a nonconstant polynomial. Then there exists a splitting field \(E\) for \(p(x)\text{.}\)

Proof

We will use mathematical induction on the degree of \(p(x)\text{.}\) If \(\deg p(x) = 1\text{,}\) then \(p(x)\) is a linear polynomial and \(E = F\text{.}\) Assume that the theorem is true for all polynomials of degree \(k\) with \(1 \leq k \lt n\) and let \(\deg p(x) = n\text{.}\) We can assume that \(p(x)\) is irreducible; otherwise, by our induction hypothesis, we are done. By Theorem \(21.5\), there exists a field \(K\) such that \(p(x)\) has a zero \(\alpha_1\) in \(K\text{.}\) Hence, \(p(x) = (x - \alpha_1)q(x)\text{,}\) where \(q(x) \in K[x]\text{.}\) Since \(\deg q(x) = n -1\text{,}\) there exists a splitting field \(E \supset K\) of \(q(x)\) that contains the zeros \(\alpha_2, \ldots, \alpha_n\) of \(p(x)\) by our induction hypothesis. Consequently,

\[ E = K(\alpha_2, \ldots, \alpha_n) = F(\alpha_1, \ldots, \alpha_n) \nonumber \]

is a splitting field of \(p(x)\text{.}\)

The question of uniqueness now arises for splitting fields. This question is answered in the affirmative. Given two splitting fields \(K\) and \(L\) of a polynomial \(p(x) \in F[x]\text{,}\) there exists a field isomorphism \(\phi : K \rightarrow L\) that preserves \(F\text{.}\) In order to prove this result, we must first prove a lemma.

Theorem \(21.32\).

Let \(\phi : E \rightarrow F\) be an isomorphism of fields. Let \(K\) be an extension field of \(E\) and \(\alpha \in K\) be algebraic over \(E\) with minimal polynomial \(p(x)\text{.}\) Suppose that \(L\) is an extension field of \(F\) such that \(\beta\) is root of the polynomial in \(F[x]\) obtained from \(p(x)\) under the image of \(\phi\text{.}\) Then \(\phi\) extends to a unique isomorphism \(\overline{\phi} : E( \alpha ) \rightarrow F( \beta )\) such that \(\overline{\phi}( \alpha ) = \beta\) and \(\overline{\phi}\) agrees with \(\phi\) on \(E\text{.}\)

Proof

If \(p(x)\) has degree \(n\text{,}\) then by Theorem \(21.13\) we can write any element in \(E( \alpha )\) as a linear combination of \(1, \alpha, \ldots, \alpha^{n - 1}\text{.}\) Therefore, the isomorphism that we are seeking must be

\[ \overline{\phi}( a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1}) = \phi(a_0) + \phi(a_1) \beta + \cdots + \phi(a_{n - 1}) \beta^{n - 1}\text{,} \nonumber \]

where

\[ a_0 + a_1 \alpha + \cdots + a_{n - 1} \alpha^{n - 1} \nonumber \]

is an element in \(E(\alpha)\text{.}\) The fact that \(\overline{\phi}\) is an isomorphism could be checked by direct computation; however, it is easier to observe that \(\overline{\phi}\) is a composition of maps that we already know to be isomorphisms.

We can extend \(\phi\) to be an isomorphism from \(E[x]\) to \(F[x]\text{,}\) which we will also denote by \(\phi\text{,}\) by letting

\[ \phi( a_0 + a_1 x + \cdots + a_n x^n ) = \phi( a_0 ) + \phi(a_1) x + \cdots + \phi(a_n) x^n\text{.} \nonumber \]

This extension agrees with the original isomorphism \(\phi : E \rightarrow F\text{,}\) since constant polynomials get mapped to constant polynomials. By assumption, \(\phi(p(x)) = q(x)\text{;}\) hence, \(\phi\) maps \(\langle p(x) \rangle\) onto \(\langle q(x) \rangle\text{.}\) Consequently, we have an isomorphism \(\psi : E[x] / \langle p(x) \rangle \rightarrow F[x]/\langle q(x) \rangle\text{.}\) By Proposition \(21.12\), we have isomorphisms \(\sigma: E[x]/\langle p(x) \rangle \rightarrow E(\alpha)\) and \(\tau : F[x]/\langle q(x) \rangle \rightarrow F( \beta )\text{,}\) defined by evaluation at \(\alpha\) and \(\beta\text{,}\) respectively. Therefore, \(\overline{\phi} = \tau \psi \sigma^{-1}\) is the required isomorphism (see Figure \(21.33\)).

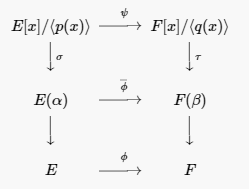
\(Figure \text { } 21.33.\)

We leave the proof of uniqueness as a exercise.

 

Theorem \(21.34\).

Let \(\phi : E \rightarrow F\) be an isomorphism of fields and let \(p(x)\) be a nonconstant polynomial in \(E[x]\) and \(q(x)\) the corresponding polynomial in \(F[x]\) under the isomorphism. If \(K\) is a splitting field of \(p(x)\) and \(L\) is a splitting field of \(q(x)\text{,}\) then \(\phi\) extends to an isomorphism \(\psi : K \rightarrow L\text{.}\)

Proof

We will use mathematical induction on the degree of \(p(x)\text{.}\) We can assume that \(p(x)\) is irreducible over \(E\text{.}\) Therefore, \(q(x)\) is also irreducible over \(F\text{.}\) If \(\deg p(x) = 1\text{,}\) then by the definition of a splitting field, \(K = E\) and \(L = F\) and there is nothing to prove.

Assume that the theorem holds for all polynomials of degree less than \(n\text{.}\) Since \(K\) is a splitting field of \(p(x)\text{,}\) all of the roots of \(p(x)\) are in \(K\text{.}\) Choose one of these roots, say \(\alpha\text{,}\) such that \(E \subset E( \alpha ) \subset K\text{.}\) Similarly, we can find a root \(\beta\) of \(q(x)\) in \(L\) such that \(F \subset F( \beta) \subset L\text{.}\) By Lemma \(21.32\), there exists an isomorphism \(\overline{\phi} : E(\alpha ) \rightarrow F( \beta)\) such that \(\overline{\phi}( \alpha ) = \beta\) and \(\overline{\phi}\) agrees with \(\phi\) on \(E\) (see Figure \(21.35\)).

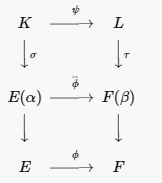
\(Figure \text { } 21.35.\)

Now write \(p(x) = (x - \alpha ) f(x)\) and \(q(x) = ( x - \beta) g(x)\text{,}\) where the degrees of \(f(x)\) and \(g(x)\) are less than the degrees of \(p(x)\) and \(q(x)\text{,}\) respectively. The field extension \(K\) is a splitting field for \(f(x)\) over \(E( \alpha)\text{,}\) and \(L\) is a splitting field for \(g(x)\) over \(F( \beta )\text{.}\) By our induction hypothesis there exists an isomorphism \(\psi : K \rightarrow L\) such that \(\psi\) agrees with \(\overline{\phi}\) on \(E( \alpha)\text{.}\) Hence, there exists an isomorphism \(\psi : K \rightarrow L\) such that \(\psi\) agrees with \(\phi\) on \(E\text{.}\)

 

Corollary \(21.36\).

Let \(p(x)\) be a polynomial in \(F[x]\text{.}\) Then there exists a splitting field \(K\) of \(p(x)\) that is unique up to isomorphism.