2.1: A First Example
- Page ID
- 97986
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
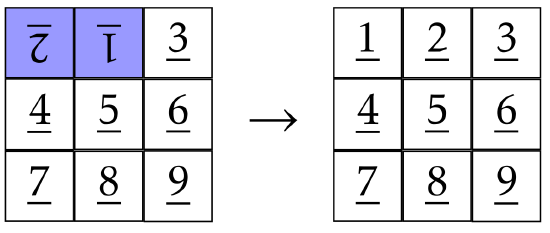
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let’s begin our study by developing some intuition about what groups actually are. To get started, we will explore the game Spinpossible, which used to be available for iOS and Android devices.* The game is played on a \(3\times 3\) board of scrambled tiles numbered 1 to 9, each of which may be right-side-up or up-side-down. The objective of the game is to return the board to the standard configuration where tiles are arranged in numerical order and right-side-up. This is accomplished by a sequence of “spins", where a spin consists of rotating an \(m\times n\) subrectangle by 180\(^\circ\). The goal is to minimize the number of spins used. The following figure depicts a scrambled board on the left and the solved board on the right. The sequence of arrows is used to denote some sequence of spins that transforms the scrambled board into the solved board.
* If you’d like to play the game, try going here: https://www.kongregate.com/games/spinpossible.↩
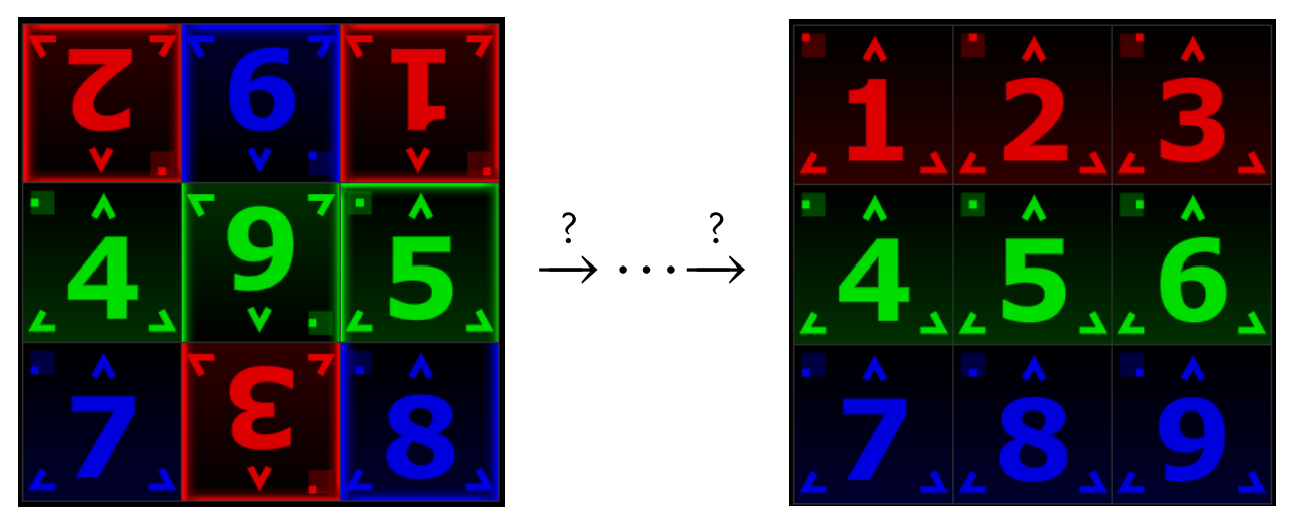
Let's play with an example. Suppose we start with the following scrambled board.
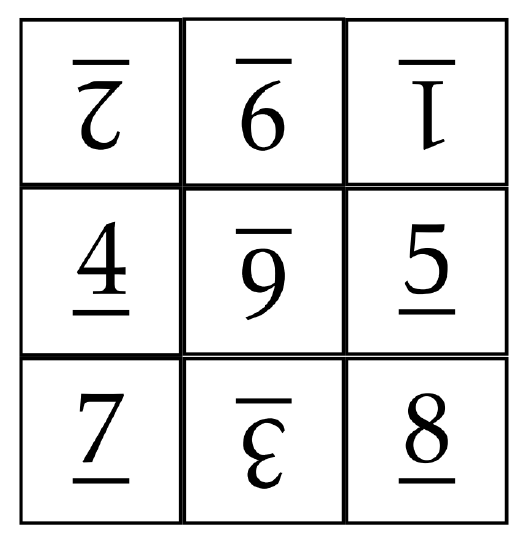
The underlines on the numbers are meant to help us tell whether a tile is right-side-up or up-side-down. Our goal is to use a sequence of spins to unscramble the board. Before we get started, let’s agree on some conventions. When we refer to tile \(n\), we mean the actual tile that is labeled by the number \(n\) regardless of its position and orientation on the board. On the other hand, position \(n\) will refer to the position on the board that tile \(n\) is supposed to be in when the board has been unscrambled. For example, in the board above, tile 1 is in position 3 and tile 7 happens to be in position 7.
It turns out that there are multiple ways to unscramble this board, but I have one particular sequence in mind. First, let’s spin the rectangle determined by the two rightmost columns. Here’s what we get. I’ve shaded the subrectangle that we are spinning.
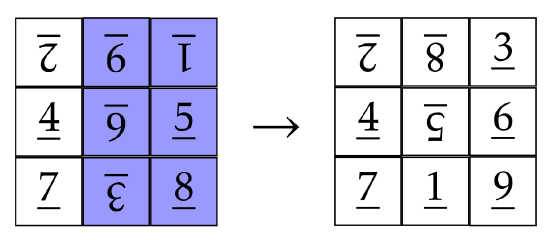
Okay, now let’s spin the middle column.
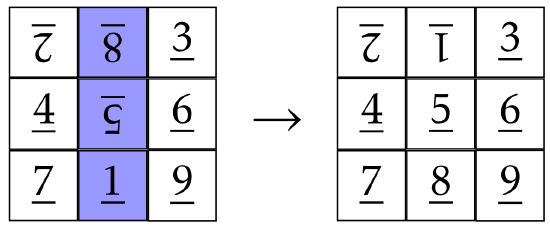
Hopefully, you can see that we are really close to unscrambling the board. All we need to do is spin the rectangle determined by the tiles in positions 1 and 2.
Putting all of our moves together, here is what we have.

In this case, we were able to solve the scrambled board in 3 moves. It’s not immediately obvious, but it turns out that there is no way to unscramble the board in fewer than 3 spins. However, there is at least one other solution that involves exactly 3 spins.
[prob:number_spinpossible_boards] How many scrambled \(3\times 3\) Spinpossible boards are there? To answer this question, you will need to rely on some counting principles such as factorials. In this context, we want to include the solved board as one of the scrambled boards—it’s just not very scrambled.
How many spins are there?
It’s useful to have some notation. Let \(s_{ij}\) denote the spin that rotates the subrectangle that has position \(i\) in the upper-left corner and position \(j\) in the lower-right corner. As an example, the sequence of spins that we used above to unscramble our initial scrambled board is \[s_{29}\to s_{28} \to s_{12}.\] As you noticed in Problem \(\PageIndex{2}\), we can also rotate a single tile. Every spin of the form \(s_{ii}\) is called a toggle. For example, \(s_{44}\) toggles the tile in position 4.
We can think of each spin as a function and since we are doing spins on top of spins, every sequence of spins corresponds to a composition of functions. We will follow the standard convention of function composition that says the function on the right goes first. In this case, our previous sequence of spins becomes \(s_{12} \circ s_{28} \circ s_{29}\), which we abbreviate as \(s_{12} s_{28} s_{29}\). This might take some getting used to, but just remember that it is just like function notation—stuff on the right goes first. We will refer to expressions like \(s_{12} s_{28} s_{29}\) as words in the alphabet \(\{s_{ij}\mid i\text{ upper left corner}, j\text{ lower right corner of subrectangle}\}\). Our words will always consist of a finite number of spins.
Every word consisting of spins corresponds to a function that takes a scrambled board as input and returns a scrambled board. We say that the words “act on" the scrambled boards. For each word, there is an associated net action. For example, the word \(s_{12} s_{23} s_{12}\) corresponds to swapping the positions but not orientation of the tiles in positions 1 and 3. You should take the time to verify this for yourself. Notice that the net action does not depend on the current configuration of the board. Sometimes it is difficult to describe what the net action associated to a word is, but there is always some corresponding net action nonetheless. Moreover, each net action has many—infinitely many, in fact—words that determine that net action. For example, it turns out that \(s_{12}s_{23}s_{12}\), \(s_{23}s_{12}s_{23}\), and \(s_{12}s_{23}s_{11}s_{11}s_{12}\) all yield the same net action. In this case, we would write \[s_{12}s_{23}s_{12}=s_{23}s_{12}s_{23}=s_{12}s_{23}s_{11}s_{11}s_{12}.\] Notice that equality here is referring to net action and not the words themselves. That is, the words are different, but the result is the same.
It is worth pointing out that \(s_{12} s_{23} s_{12}\) is not itself a spin. However, sometimes a composition of spins will yield a spin. For example, the net action of \(s_{12} s_{11} s_{12}\) is toggling the tile in position 2. That is, \(s_{12} s_{11} s_{12}=s_{22}\).
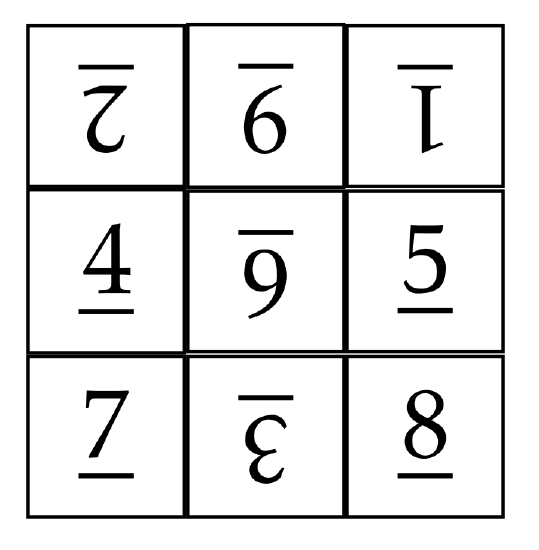
Find a sequence of 3 spins that is different from the one we described earlier that unscrambles the following board. Write your answer as a word consisting of spins.
What is the net action that corresponds to the word \(s_{23} s_{12} s_{23}\)? What can you conclude about \(s_{23} s_{12} s_{23}\) compared to \(s_{12} s_{23} s_{12}\)?
We can also use exponents to abbreviate. For example, \(s_{23}^2\) is the same as \(s_{23} s_{23}\) (which in this case is the net action of doing nothing) and \((s_{12} s_{23})^2\) is the same as \(s_{12} s_{23} s_{12} s_{23}\).
It turns out that there is an even simpler word (i.e., a shorter word) that yields the same net action as \((s_{12} s_{23})^2\). Can you find one?
Define \(\text{Spin}_{3\times 3}\) to be the collection of net actions that we can obtain from words consisting of spins. We say that the set of spins generates \(\text{Spin}_{3\times 3}\) and we refer to the set of spins as a generating set for \(\text{Spin}_{3\times 3}\).
Suppose \(s_{x_1}s_{x_2}\cdots s_{x_n}\) and \(s_{y_1}s_{y_2}\cdots s_{y_m}\) are both words consisting of spins. Then the corresponding net actions, say \(u\) and \(v\), respectively, are elements of \(\text{Spin}_{3\times 3}\). Prove that the composition of the actions \(u\) and \(v\) is an element of \(\text{Spin}_{3\times 3}\).
The previous problem tells us that the composition of two net actions from \(\text{Spin}_{3\times 3}\) results in another net action in \(\text{Spin}_{3\times 3}\). Formally, we say that \(\text{Spin}_{3\times 3}\) is closed under composition.
It is clear that we can construct an infinite number of words consisting of spins, but since there are a finite number of ways to rearrange the positions and orientations of the tiles of the \(3\times 3\) board, there are only a finite number of net actions arising from these words. That is, \(\text{Spin}_{3\times 3}\) is a finite set of functions.
Verify that \(\text{Spin}_{3\times 3}\) contains an identity function, i.e., a function whose net action is “do nothing." What happens if we compose a net action from \(\text{Spin}_{3\times 3}\) with the identity?
A natural question to ask is whether every possible scrambled Spinpossible board can be unscrambled using only spins. In other words, is \(\text{Spin}_{3\times 3}\) sufficient to unscramble every scrambled board? It turns out that the answer is yes.
Verify that \(\text{Spin}_{3\times 3}\) is sufficient to unscramble every scrambled board by describing an algorithm that will always unscramble a scrambled board. It does not matter whether your algorithm is efficient. That is, we don’t care how many steps it takes to unscramble the board as long as it works in a finite number of steps. Using your algorithm, what is the maximum number of spins required to unscramble any scrambled board?
In a 2011 paper, Alex Sutherland and Andrew Sutherland (a father and son team) present a number of interesting results about Spinpossible and list a few open problems. You can find the paper at http://arxiv.org/abs/1110.6645. As a side note, Alex is one of the developers of the game and his father, Andrew, is a mathematics professor at MIT. Using a brute-force computer algorithm, the Sutherlands verified that every scrambled \(3\times 3\) Spinpossible board can be solved in at most 9 moves. However, a human readable mathematical proof of this fact remains elusive. By the way, mathematics is chock full of open problems and you can often get to the frontier of what is currently known without too much trouble. Mathematicians are in the business of solving open problems.
Instead of unscrambling boards, we can act on the solved board with an action from \(\text{Spin}_{3\times 3}\) to obtain a scrambled board. Problem \(\PageIndex{8}\) tells us that we can use \(\text{Spin}_{3\times 3}\) to get from the solved board to any scrambled board. In fact, starting with the solved board makes it clear that there is a one-to-one correspondence between net actions and scrambled boards.
What is the size of \(\text{Spin}_{3\times 3}\)? That is, how many net actions are in \(\text{Spin}_{3\times 3}\)?
Let’s make a couple more observations. First, every spin is reversible. That is, every spin has an inverse. In the case of Spinpossible, we can just apply the same spin again to undo it. For example, \(s_{12}^2\) is the same as doing nothing. This means that the inverse of \(s_{12}\), denoted \(s_{12}^{-1}\), is \(s_{12}\) itself. Symbolically, we write \(s_{12}^{-1}=s_{12}\). Remember that we are exploring the game Spinpossible—it won’t always be the case that repeating an action will reverse the action.
In the same vein, every sequence of spins is reversible. For example, if we apply \(s_{12} s_{23}\) (i.e., do \(s_{23}\) first followed by \(s_{12}\)), we could undo the net action by applying \(s_{23} s_{12}\) because \[(s_{12} s_{23})^{-1}=s_{23}^{-1} s_{12}^{-1}=s_{23} s_{12}\] since \(s_{23}^{-1}=s_{23}\) and \(s_{12}^{-1}=s_{12}\). Notice that the first equality is an instantiation of the “socks and shoes theorem", which states that if \(f\) and \(g\) are functions with compatible domain and codomain, then \[(f\circ g)^{-1} = g^{-1}\circ f^{-1}.\] The upshot is that the net action that corresponds to a word consisting of spins can be reversed by applying “socks and shoes" and is itself an action.
Imagine we started with the solved board and then you scrambled the board according to some word consisting of spins. Let’s call this word \(w\). How could you obtain the solved board from the scrambled board determined by \(w\)? How is this related to \(w^{-1}\)?
There is one detail we have been sweeping under the rug. Notice that every time we wrote down a word consisting of two or more spins, we didn’t bother to group pairs of adjacent spins using parentheses. Recall that the composition of functions with compatible domains and codomains is associative (see Theorem 2.2.1). That is, if \(f\), \(g\), and \(h\) are functions with compatible domains and codomains, then \[(f\circ g)\circ h = f\circ (g\circ h).\] Since composition of spins is really just function composition, composition of spins is also associative. And since the spins generate \(\text{Spin}_{3\times 3}\), the composition of net actions from \(\text{Spin}_{3\times 3}\) is associative, as well.
Does the order in which you apply spins matter? Does it always matter? Let’s be as specific as possible. If the order in which we apply two spins does not matter, then we say that the spins commute. However, if the order does matter, then the spins do not commute. When will two spins commute? When will they not commute? Provide some specific examples.
In the previous problem, you discovered that the composition of two spins may or may not commute. Since the spins generate \(\text{Spin}_{3\times 3}\), the composition of two net actions may or may not commute. We say that \(\text{Spin}_{3\times 3}\) is not commutative.
Let’s collect our key observations about \(\text{Spin}_{3\times 3}\).
- Generating Set: The set of spins generates \(\text{Spin}_{3\times 3}\). That is, every net action from \(\text{Spin}_{3\times 3}\) corresponds to a word consisting of spins.1
- Closure: The composition of any two net actions from \(\text{Spin}_{3\times 3}\) results in a net action from \(\text{Spin}_{3\times 3}\).
- Associative: The composition of net actions from \(\text{Spin}_{3\times 3}\) is associative.
- Identity: There is an identity in \(\text{Spin}_{3\times 3}\) whose corresponding net action is “do nothing".
- Inverses: Every net action from \(\text{Spin}_{3\times 3}\) has an inverse net action in \(\text{Spin}_{3\times 3}\). Composing a net action and its inverse results in the identity.
- The composition of two net actions from \(\text{Spin}_{3\times 3}\) may or may not commute.
It turns out that \(\text{Spin}_{3\times 3}\) is an example of a group. Loosely speaking, a group is a set together with a method for combining two elements together that satisfies conditions (2), (3), (4), and (5) above. More formally, a group is a nonempty set together with an associative binary operation such that the set contains an identity element and every element in the set has an inverse that is also in the set. As we shall see, groups can have a variety of generating sets, possibly of different sizes. Also, some groups are commutative and some groups are not.
Before closing out this section, let’s tackle a few more interesting problems concerning Spinpossible. We say that a generating set \(S\) for a group is a minimal generating set if \(S\setminus\{x\}\) is no longer a generating set for the group for all \(x\in S\).
Determine whether the set of spins is a minimal generating set for \(\text{Spin}_{3\times 3}\).
- *
-
The case of Spinpossible is a little misleading. Since each spin is its own inverse, we never need to write words consisting of spins with inverses. However, as we shall see later, there are situations outside the context of Spinpossible where we will need to utilize inverses of elements from a generating set.
It’s not too difficult to prove—but we will omit the details—that we can generate \(\text{Spin}_{3\times 3}\) with the following subset of 9 spins: \[T=\{s_{11}, s_{12}, s_{23}, s_{36}, s_{56}, s_{45}, s_{47}, s_{78}, s_{89}\}.\] That is, every net action in \(\text{Spin}_{3\times 3}\) corresponds to a word consisting of the spins from \(T\). Try to take a moment to convince yourself that this is at least plausible.
For each of the following spins, find a word consisting of spins from the set \(T\) that yields the same net action.
- \(s_{33}\)
- \(s_{13}\)
- \(s_{14}\)
Taking for granted that \(T\) is a generating set for \(\text{Spin}_{3\times 3}\), determine whether \(T\) is a minimal generating set.


