4.4: Alternating Groups

In this section, we describe a special class of permutation groups. To get started, let’s play with a few exercises.

Problem \(\PageIndex{1}\)

Write down every permutation in \(S_3\) as a product of 2-cycles in the most efficient way you can find (i.e., use the fewest possible transpositions). Now, write every permutation in \(S_3\) as a product of adjacent 2-cycles, but don’t worry about whether your decompositions are efficient. Any observations about the number of transpositions you used in each case? Think about even versus odd.

Theorem \(\PageIndex{1}\)

If \(\alpha_1,\alpha_2,\ldots,\alpha_k\) is a collection of 2-cycles in \(S_n\) such that \(\alpha_1\alpha_2\cdots\alpha_k=(1)\), then \(k\) must be even.

Proof.

Suppose \(\alpha_1,\alpha_2,\ldots,\alpha_k\) is a collection of 2-cycles in \(S_n\) such that \(\alpha_1\alpha_2\cdots\alpha_k=(1)\). We need to show that \(k\) is even. We proceed by strong induction. First, it is clear that the statement is not true when \(k=1\), but is true when \(k=2\).

Now, assume that \(k>2\) and if \(j\leq k-1\) and we have a product of \(j\) 2-cycles that equals the identity, then \(j\) is even. Consider \(\alpha_1\alpha_2\). The only possibilities are:

1. \(\alpha_1\alpha_2=(a,b)(a,b)\),
2. \(\alpha_1\alpha_2=(a,b)(a,c)\),
3. \(\alpha_1\alpha_2=(a,b)(c,d)\),
4. \(\alpha_1\alpha_2=(a,b)(b,c)\).

If case (i) happens, then \[(1)=\alpha_1\alpha_2\cdots\alpha_k=\alpha_3\alpha_4\cdots\alpha_k.\] Since the expression on the right consists of \(k-2\) factors, \(k-2\) must be even by induction, which implies that \(k\) is even. Now, suppose we are in one of cases (ii), (iii), or (iv). Observe that:

1. \((a,b)(a,c)=(b,c)(a,b)\),
2. \((a,b)(c,d)=(c,d)(a,b)\),
3. \((a,b)(b,c)=(b,c)(a,c)\).

In each case, we were able to move \(a\) from the original left 2-cycle to a new right 2-cycle. That is, we were able to rewrite \(\alpha_1\alpha_2\) so that \(a\) does not appear in the left 2-cycle. Systematically repeat this process for the pairs \(\alpha_2\alpha_3\), \(\alpha_3\alpha_4\),…, \(\alpha_{k-1}\alpha_k\). If we ever encounter case (i) along the way, then we are done by induction. Otherwise, we are able to rewrite \(\alpha_1\alpha_2\cdots\alpha_k\) so that \(a\) only appears in the rightmost 2-cycle. But this implies that \(\alpha_1\alpha_2\cdots\alpha_k\) does not fix \(a\), which contradicts \(\alpha_1\alpha_2\cdots\alpha_k =(1)\). This implies that at some point we must encounter case (i), and hence \(k\) is even by induction.

Theorem \(\PageIndex{2}\)

If \(\sigma\in S_n\), then every transposition representation of \(\sigma\) has the same parity.

The previous theorem tells us that the following definition is well-defined.

Definition: Even and Odd Permutation

A permutation is even (respectively, odd) if one of its transposition representations consists of an even (respectively, odd) number of transpositions.

Problem \(\PageIndex{2}\)

Classify all of the permutations in \(S_3\) as even or odd.

Problem \(\PageIndex{3}\)

Classify all of the permutations in \(S_4\) as even or odd.

Problem \(\PageIndex{4}\)

Determine whether \((1,4,2,3,5)\) is even or odd. How about \((1,4,2,3,5)(7,9)\)?

Problem \(\PageIndex{5}\)

Consider the arbitrary \(k\)-cycle \((a_1,a_2,\ldots, a_k)\) from \(S_n\) (with \(k\leq n\)). When will this cycle be odd versus even? Briefly justify your answer.

Problem \(\PageIndex{6}\)

Conjecture a statement about when a permutation will be even versus odd. Briefly justify your answer.

And finally, we are ready to introduce the alternating groups.

Definition: Alternating Groups

The set of all even permutations in \(S_n\) is denoted by \(A_n\) and is called the alternating group.

Since we referred to \(A_n\) as a group, it darn well better be a group!

Theorem \(\PageIndex{3}\)

The set \(A_n\) forms a group under composition of permutations and has order \(n!/2\).*

*

Hint: To show that \(A_n\) is a group, argue that \(A_n\) is a subgroup of \(S_n\) using the Two-Step Subgroup Test (see Theorem [thm:subgroup_criterion]). To show that \(|A_n|=n!/2\), prove that the number of even permutations in \(S_n\) is the same as the number of odd permutations in \(S_n\). Here is one way to accomplish this. Define \(f:A_n\to S_n\setminus A_n\) via \(f(\sigma)=(1,2)\sigma\). Note that \(S_n\setminus A_n\) is the set of odd permutations in \(S_n\). Show that \(f\) is a bijection.

Problem \(\PageIndex{7}\)

Find \(A_3\). What group is \(A_3\) isomorphic to?

Problem \(\PageIndex{8}\)

Find \(A_4\) and then draw its subgroup lattice. Is \(A_4\) abelian?

Problem \(\PageIndex{9}\)

What is the order of \(A_5\)? Is \(A_5\) abelian?

Problem \(\PageIndex{10}\)

What orders of elements occur in \(S_6\) and \(A_6\)? What about \(S_7\) and \(A_7\)?

Problem \(\PageIndex{11}\)

Does \(A_8\) contain an element of order 15? If so, find one. If not, explain why no such element exists.

Remark \(\PageIndex{1}\)

Below are a few interesting facts about \(A_4\) and \(A_5\), which we will state without proof.

1. The group of rigid motion symmetries for a regular tetrahedron is isomorphic to \(A_4\).
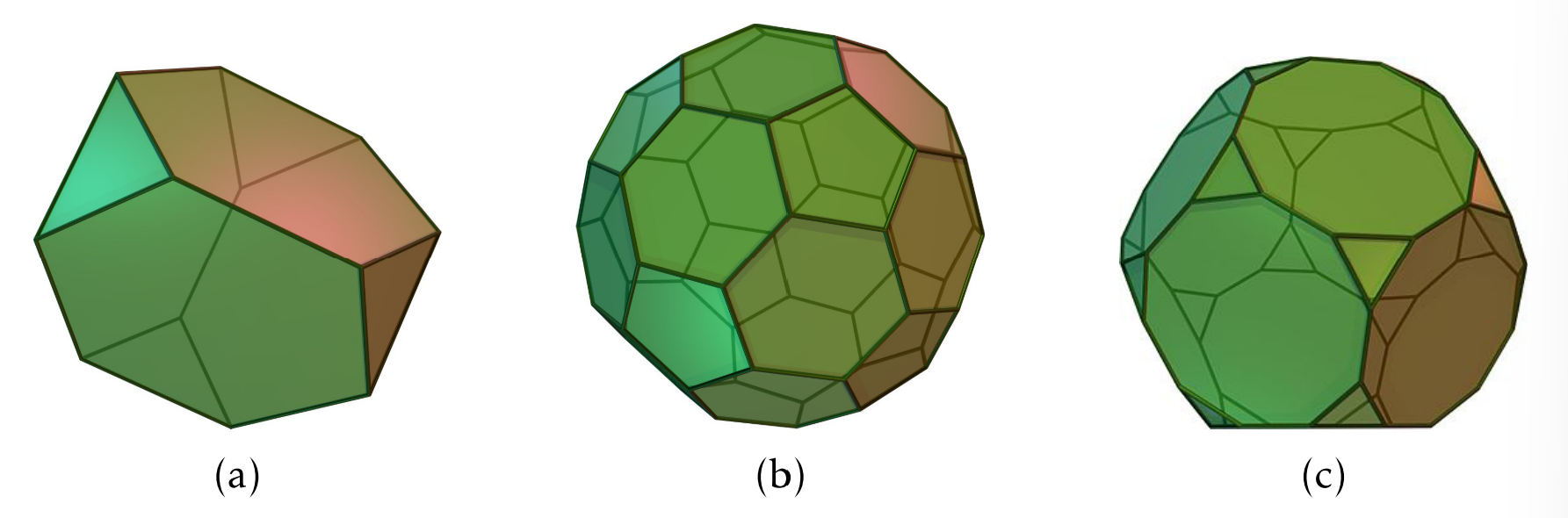
2. You can arrange the Cayley diagram for \(A_4\) with generators \((1,2)(3,4)\) and \((2,3,4)\) on a truncated tetrahedron, which is depicted in Figure \(\PageIndex{1}\)a.
3. You can arrange the Cayley diagram for \(A_5\) with generators \((1,2)(3,4)\) and \((1,2,3,4,5)\) on a truncated icosahedron, which is given in Figure \(\PageIndex{1}\)b. You can also arrange the Cayley diagram for \(A_5\) with generators \((1,2,3)\) and \((1,5)(2,4)\) on a truncated dodecahedron seen in Figure \(\PageIndex{1}\)c.

Figure \(\PageIndex{1}\): Truncated tetrahedron, truncated icosahedron, and truncated dodecahedron. [Image source: Wikipedia]