5.1: Cosets
- Page ID
- 98000
Undoubtably, you’ve noticed numerous times that if \(G\) is a group with \(H\leq G\) and \(g\in G\), then both \(|H|\) and \(|g|\) divide \(|G|\). The theorem that says this is always the case is called Lagrange’s theorem and we’ll prove it towards the end of this chapter. We begin with a definition.
Let \(G\) be a group and let \(H\leq G\) and \(a\in G\). The subsets \[aH:=\{ah\mid h\in H\}\] and \[Ha:=\{ha\mid h\in H\}\] are called the left and right cosets of \(H\) containing \(a\), respectively.
To gain some insight, let’s tinker with an example. Consider the dihedral group \(D_3=\langle r,s\rangle\) and let \(H=\langle s\rangle\leq D_3\). To compute the right cosets of \(H\), we need to multiply all of the elements of \(H\) on the right by the elements of \(G\). We see that \[\begin{aligned} & He =\{ee,se\}=\{e,s\}=H\\ & Hr=\{er,sr\}=\{r,sr\}\\ & Hr^2=\{er^2,sr^2\}=\{r^2,rs\}\\ & Hs=\{es,ss\}=\{s,e\}=H\\ & Hsr=\{esr,ssr\}=\{sr,r\}\\ & Hrs=\{ers,srs\}=\{rs,ssr^2\}=\{rs,r^2\}.\end{aligned}\] Despite the fact that we made six calculations (one for each element in \(D_3\)), if we scan the list, we see that there are only 3 distinct cosets, namely \[\begin{aligned} & H=He=Hs=\{e,s\}\\ & Hr=Hsr=\{r,sr\}\\ & Hr^2=Hrs=\{r^2,rs\}.\end{aligned}\] We can make a few more observations. First, the resulting cosets formed a partition of \(D_3\). That is, every element of \(D_3\) appears in exactly one coset. Moreover, all the cosets are the same size—two elements in each coset in this case. Lastly, each coset can be named in multiple ways. In particular, the elements of the coset are exactly the elements of \(D_3\) we multiplied \(H\) by. For example, \(Hr=Hsr\) and the elements of this coset are \(r\) and \(sr\). Shortly, we will see that these observations hold, in general.
Here is another significant observation we can make. Consider the Cayley diagram for \(D_3\) with generating set \(\{r,s\}\) that is given in Figure \(\PageIndex{1}\). Given this Cayley diagram, we can visualize the subgroup \(H\) and its clones. Moreover, \(H\) and its clones are exactly the 3 right cosets of \(H\). We’ll see that, in general, the right cosets of a given subgroup are always the subgroup and its clones (see Problem \(\PageIndex{7}\)).
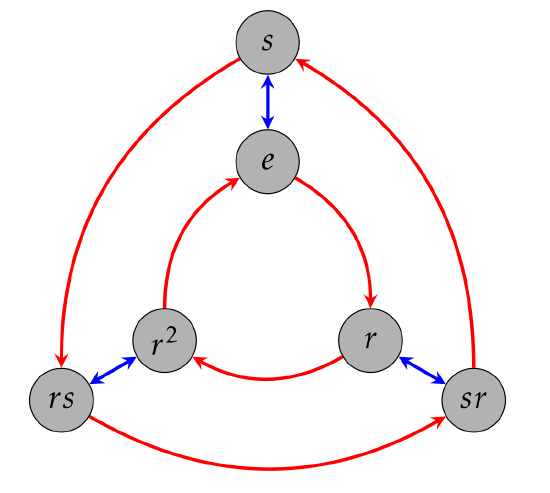
Consider the group \(D_3\). Find all the left cosets for \(H=\langle s\rangle\). Are they the same as the right cosets? Are they the same as the subgroup \(H\) and its clones that we can see in the Cayley graph for \(D_3\) with generating set \(\{r,s\}\)?
As the previous exercise indicates, the collections of left and right cosets may not be the same and when they are not the same, the subgroup and its clones do not coincide with the left cosets.
You might be thinking that somehow right cosets are “better" than left cosets since we were able to visualize them in the Cayley graph. However, this is just a consequence of our convention of composing actions from right to left. If we had adopted a left to right convention, then we would be able to visualize the left cosets in Cayley diagrams.
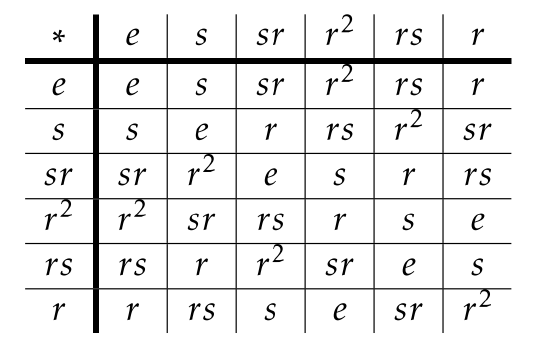
Computing left and right cosets using a group table is fairly easy. Hopefully, you figured out in Problem \(\PageIndex{1}\) that the left cosets of \(H=\langle s\rangle\) in \(D_3\) are \(H=\{e,s\}\), \(srH=\{r^2,sr\}\), and \(rsH=\{r,rs\}\). Now, consider the following group table for \(D_3\) that has the rows and columns arranged according to the left cosets of \(H\).
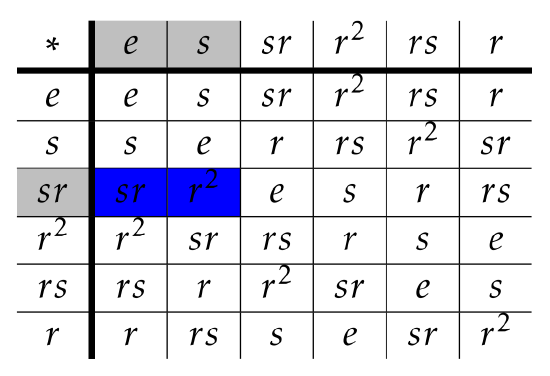
The left coset \(srH\) must appear in the row labeled by \(sr\) and in the columns labeled by the elements of \(H=\{e,s\}\). We’ve depicted this below.
On the other hand, the right coset \(Hsr\) must appear in the column labeled by \(sr\) and the rows labeled by the elements of \(H=\{e,s\}\):
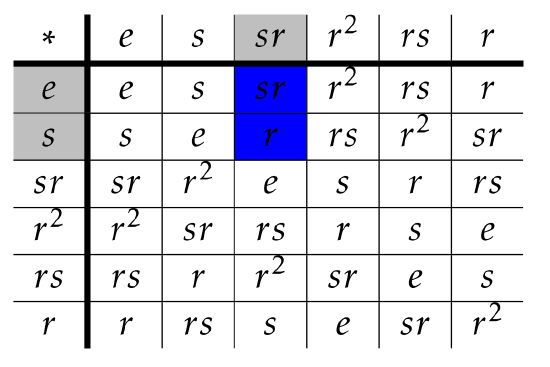
As we can see from the tables, \(srH\neq Hsr\) since \(\{sr,r^2\}\neq \{sr,r\}\). If we color the entire group table for \(D_3\) according to which left coset an element belongs to, we get the following.
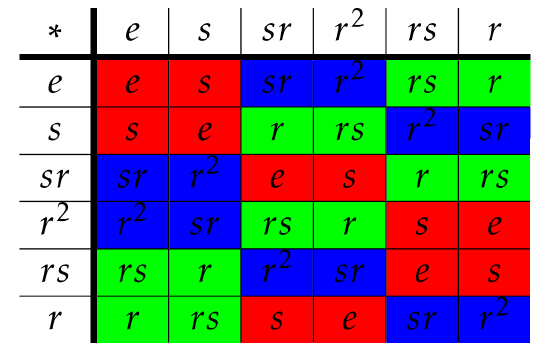
We would get a similar table (but in this case, not identical) if we colored the elements according to the right cosets.
Let’s tackle a few more examples.
Consider \(D_3\) and let \(K=\langle r\rangle\).
- Find all of the left cosets of \(K\) and then find all of the right cosets of \(K\) in \(D_3\). Any observations?
- Write down the group table for \(D_3\), but this time arrange the rows and columns according to the left cosets for \(K\). Color the entire table according to which left coset an element belongs to. Can you visualize the observations you made in part (a)?
Consider \(Q_8\). Let \(H=\langle i\rangle\) and \(K=\langle -1\rangle\).
- Find all of the left cosets of \(H\) and all of the right cosets of \(H\) in \(Q_8\).
- Write down the group table for \(Q_8\) so that rows and columns are arranged according to the left cosets for \(H\). Color the entire table according to which left coset an element belongs to.
- Find all of the left cosets of \(K\) and all of the right cosets of \(K\) in \(Q_8\).
- Write down the group table for \(Q_8\) so that rows and columns are arranged according to the left cosets for \(K\). Color the entire table according to which left coset an element belongs to.
Consider \(S_4\). Find all of the left cosets and all of the right cosets of \(A_4\) in \(S_4\). Instead of doing brute-force, try to be clever. Hint: What happens when you compose two even permutations versus an even permutation and an odd permutation?
Consider \(\mathbb{Z}_8\). Find all of the left cosets and all of the right cosets of \(\langle 4\rangle\) in \(\mathbb{Z}_8\). Why do you know the left and right cosets are the same without actually verifying?
Consider \((\mathbb{Z},+)\). Find all of the left cosets and all of the right cosets of \(3\mathbb{Z}\) in \(\mathbb{Z}\). Why do you know the left and right cosets are the same without actually verifying?
Let \(G\) be a group and let \(H\leq G\). If \(G\) is abelian, then for all \(a\in G\), \(aH=Ha\). That is, if \(G\) is abelian, then the left cosets of \(H\) are the same as the right cosets of \(H\).
Exercises \(\PageIndex{1}\) and \(\PageIndex{2}\) illustrate that if a group is non-abelian, then the cosets of a subgroup may or may not coincide. That is, knowing that the group is non-abelian is not enough to determine whether the left and right cosets are different.
In all of the examples we’ve seen so far, the left and right cosets partitioned \(G\) into equal-sized chunks. We need to prove that this is true in general. To prove that the cosets form a partition, we will define an appropriate equivalence relation.
Let \(G\) be a group and let \(H\leq G\). Define \(\sim_L\) and \(\sim_R\) via
\(a\sim_L b\) if and only if \(a^{-1}b\in H\)
and
\(a\sim_R b\) if and only if \(ab^{-1}\in H\).
Then both \(\sim_L\) and \(\sim_R\) are equivalence relations.*
- *
-
You only need to prove that either \(\sim_L\) or \(\sim_R\) is an equivalence relation as the proof for the other is similar.
Since \(\sim_L\) and \(\sim_R\) are equivalence relations, the corresponding equivalence classes form a partition of \(G\). If \(a\in G\), then the “left" and “right" equivalence classes containing \(a\) are given by \[[a]_{\sim_L}=\{g\in G\mid a\sim_L g\}\] and \[[a]_{\sim_R}=\{g\in G\mid a\sim_R g\}.\] The next theorem tells us that the equivalence classes determined by \(\sim_L\) and \(\sim_R\) are indeed the left and right cosets of \(H\leq G\), respectively.
If \(G\) is a group and \(H\leq G\), then \([a]_{\sim_L}=aH\) and \([a]_{\sim_R}=Ha\) for all \(a\in G\).
If \(G\) is a group and \(H\leq G\), then the left (respectively, right) cosets of \(H\) form a partition of \(G\).
Next, we argue that all of the cosets have the same size.
Let \(G\) be a group, \(H\leq G\), and \(a\in G\). Define \(\phi:H\to aH\) via \(\phi(h)=ah\). Then \(\phi\) is one-to-one and onto.
Let \(G\) be a group and let \(H\leq G\). Then all of the left and right cosets of \(H\) are the same size as \(H\). In other words \(\#(aH)=|H|=\#(Ha)\) for all \(a\in G\).*
- *
-
As you probably expect, \(\#(aH)\) denotes the size of \(aH\). Note that everything works out just fine even if \(H\) has infinite order.
The next theorem provides a useful characterization of cosets. Each part can either be proved directly or by appealing to previous results in this section.
Let \(G\) be a group and let \(H\leq G\).
- If \(a\in G\), then \(a\in aH\) (respectively, \(Ha\)).
- We have \(b\in aH\) (respectively, \(Ha\)) if and only if \(aH=bH\) (respectively, \(Ha=Hb\)).
- If \(a\in H\), then \(aH=H=Ha\).
- If \(a\notin H\), then for all \(h\in H\), \(ah\notin H\) (respectively, \(ha \notin H\)).
The upshot of part (b) of Theorem \(\PageIndex{4}\) is that cosets can have different names. In particular, if \(b\) is an element of the left coset \(aH\), then we could have just as easily called the coset by the name \(bH\). In this case, both \(a\) and \(b\) are called coset representatives.
The final result of this section verifies that the clones of a subgroup in a Cayley diagram coincide with the right cosets of the subgroup.
Let \(G\) be a finite group with generating set \(S\) and let \(H\) be a proper subgroup of \(G\) and suppose we can visualize the subgroup for \(H\) in the Cayley diagram for \(G\) using \(S\) as the generating set.
- If \(g\in G\), verify that the right coset \(Hg\) is a clone of \(H\). Hint: Suppose \(s\in S\) and \(h_1, h_2\in H\) such that there is an arrow labeled by \(s\) that points from \(h_1\) to \(h_2\). Argue that there is an arrow labeled by \(s\) pointing from \(h_1g\) to \(h_2g\).
- If \(C\) is a clone of \(H\), prove that \(C\) is a right coset of \(H\).


