7.1: Homomorphisms

Let \(G_1\) and \(G_2\) be groups. Recall that \(\phi:G_1\to G_2\) is an isomorphism if and only if \(\phi\)

1. is one-to-one,
2. is onto, and
3. satisfies the homomorphic property.

We say that \(G_1\) is isomorphic to \(G_2\) and write \(G_1\cong G_2\) if such a \(\phi\) exists. Loosely speaking, two groups are isomorphic if they have the “same structure." What if we drop the one-to-one and onto requirement?

Definition: Homomorphism

Let \((G_1,*)\) and \((G_2,\odot)\) be groups. A function \(\phi:G_1\to G_2\) is a homomorphism if and only if \(\phi\) satisfies the homomorphic property: \[\phi(x*y)=\phi(x)\odot\phi(y)\] for all \(x,y\in G_1\). At the risk of introducing ambiguity, we will usually omit making explicit reference to the binary operations and write the homomorphic property as \[\phi(xy)=\phi(x)\phi(y).\]

Group homomorphisms are analogous to linear transformations on vector spaces that one encounters in linear algebra.

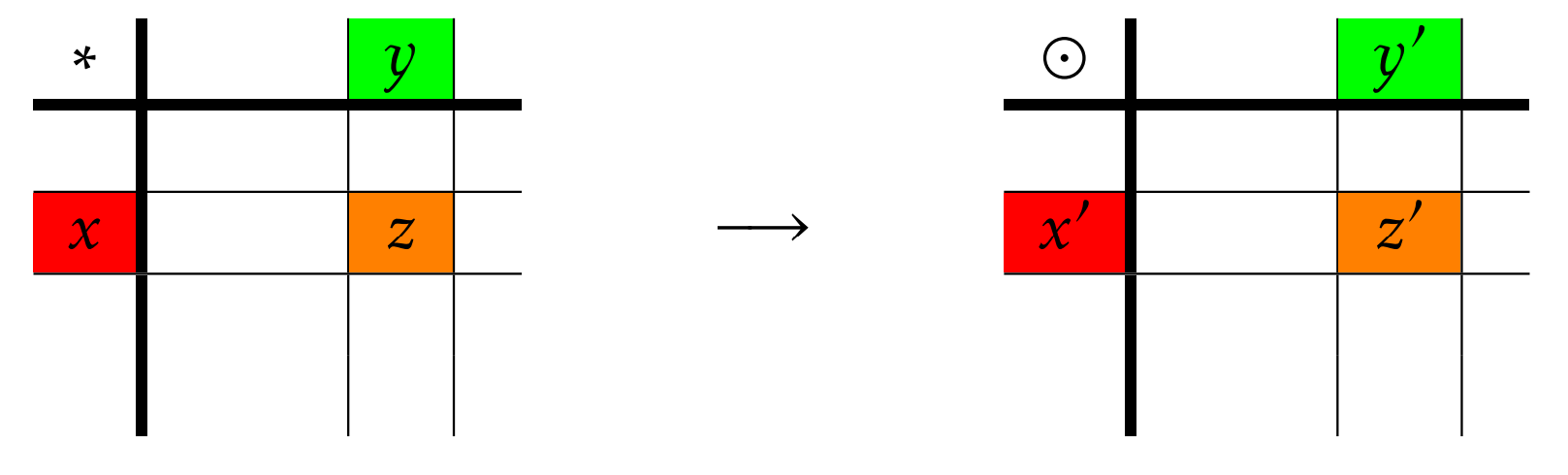
Figure \(\PageIndex{1}\) captures a visual representation of the homomorphic property. We encountered this same representation in Figure \(\PageIndex{1}\). If \(\phi(x)=x'\), \(\phi(y)=y'\), and \(\phi(z)=z'\) while \(z'=x'\odot y'\), then the only way \(G_2\) may respect the structure of \(G_1\) is for \[\phi(x*y)=\phi(z)=z'=x'\odot y'=\phi(x)\odot \phi(y).\]

Figure \(\PageIndex{1}\)

Problem \(\PageIndex{1}\): Homomorphism

Define \(\phi:\mathbb{Z}_3\to D_3\) via \(\phi(k)=r^k\). Prove that \(\phi\) is a homomorphism and then determine whether \(\phi\) is one-to-one or onto. Also, try to draw a picture of the homomorphism in terms of Cayley diagrams.

Problem \(\PageIndex{2}\)

Let \(G\) and \(H\) be groups. Prove that the function \(\phi:G\times H\to G\) given by \(\phi(g,h)=g\) is a homomorphism. This function is an example of a projection map.

There is always at least one homomorphism between two groups.

Theorem \(\PageIndex{1}\): Trivial Homomorphism

Let \(G_1\) and \(G_2\) be groups. Define \(\phi:G_1\to G_2\) via \(\phi(g)=e_2\) (where \(e_2\) is the identity of \(G_2\)). Then \(\phi\) is a homomorphism. This function is often referred to as the trivial homomorphism or the \(0\)-map.

Back in Section 3.3, we encountered several theorems about isomorphisms. However, at the end of that section we remarked that some of those theorems did not require that the function be one-to-one and onto. We collect those results here for convenience.

Theorem \(\PageIndex{2}\)

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism.

1. If \(e_1\) and \(e_2\) are the identity elements of \(G_1\) and \(G_2\), respectively, then \(\phi(e_1)=e_2\).
2. For all \(g\in G_1\), we have \(\phi(g^{-1})=[\phi(g)]^{-1}\).
3. If \(H\leq G_1\), then \(\phi(H)\leq G_2\), where \[\phi(H):=\{y\in G_2\mid \text{there exists } h\in H\text{ such that }\phi(h)=y\}.\] Note that \(\phi(H)\) is called the image of \(H\). A special case is when \(H=G_1\). Notice that \(\phi\) is onto exactly when \(\phi(G_1)=G_2\).

The following theorem is a consequence of Lagrange’s Theorem.

Theorem \(\PageIndex{3}\)

Let \(G_1\) and \(G_2\) be groups such that \(G_2\) is finite and let \(H\leq G_1\). If \(\phi:G_1\to G_2\) is a homomorphism, then \(|\phi(H)|\) divides \(|G_2|\).

The next theorem tells us that under a homomorphism, the order of the image of an element must divide the order of the pre-image of that element.

Theorem \(\PageIndex{4}\): Order Image

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. If \(g\in G_1\) such that \(|g|\) is finite, then \(|\phi(g)|\) divides \(|g|\).

Every homomorphism has an important subset of the domain associated with it.

Definition: Kernel

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. The kernel of \(\phi\) is defined via \[\ker(\phi):=\{g\in G_1\mid \phi(g)=e_2\}.\]

The kernel of a homomorphism is analogous to the null space of a linear transformation of vector spaces.

Problem \(\PageIndex{3}\)

Identify the kernel and image for the homomorphism given in Problem \(\PageIndex{1}\).

Problem \(\PageIndex{4}\)

What is the kernel of a trivial homomorphism (see Theorem \(\PageIndex{1}\)).

Theorem \(\PageIndex{5}\): Kernal Normal

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. Then \(\ker(\phi)\trianglelefteq G_1\).

Theorem \(\PageIndex{6}\): Canonical Projection

Let \(G\) be a group and let \(H\trianglelefteq G\). Then the map \(\gamma:G\to G/H\) given by \(\gamma(g)=gH\) is a homomorphism with \(\ker(\gamma)=H\). This map is called the canonical projection map.

The upshot of Theorems \(\PageIndex{5}\) and \(\PageIndex{6}\) is that kernels of homomorphisms are always normal and every normal subgroup is the kernel of some homomorphism. It turns out that the kernel can tell us whether \(\phi\) is one-to-one.

The next theorem tells us that two elements in the domain of a group homomorphism map to the same element in the codomain if and only if they are in the same coset of the kernel.

Theorem \(\PageIndex{7}\): Same Image

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. Then \(\phi(a) = \phi(b)\) if and only if \(a\in b\ker(\phi)\).

One consequence of Theorem \(\PageIndex{7}\) is that if the kernel of a homomorphism has order \(k\), then the homomorphism is \(k\)-to-1. That is, every element in the range has exactly \(k\) elements from the domain that map to it. In particular, each of these collections of \(k\) elements corresponds to a coset of the kernel.

Problem \(\PageIndex{5}\)

Suppose \(\phi:\mathbb{Z}_{20}\to\mathbb{Z}_{20}\) is a group homomorphism such that \(\ker(\phi)=\{0,5,10,15\}\). If \(\phi(13)=8\), determine all elements that \(\phi\) maps to 8.

The next result is a special case of Theorem \(\PageIndex{7}\).

Theorem \(\PageIndex{8}\): Trivial Kernel

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. Then \(\phi\) is one-to-one if and only if \(\ker(\phi)=\{e_1\}\), where \(e_1\) is the identity in \(G_1\).

Let \(G_1\) and \(G_2\) be groups and suppose \(\phi:G_1\to G_2\) is a homomorphism. Given a generating set for \(G_1\), the homomorphism \(\phi\) is uniquely determined by its action on the generating set for \(G_1\). In particular, if you have a word for a group element written in terms of the generators, just apply the homomorphic property to the word to find the image of the corresponding group element.

Problem \(\PageIndex{6}\): \(Q_8\to V_{4}\)

Suppose \(\phi: Q_8\to V_{4}\) is a group homomorphism satisfying \(\phi(i)=h\) and \(\phi(j)=v\).

1. Find \(\phi(1)\), \(\phi(-1)\), \(\phi(k)\), \(\phi(-i)\), \(\phi(-j)\), and \(\phi(-k)\).
2. Find \(\ker(\phi)\).
3. What well-known group is \(Q_8/\ker(\phi)\) isomorphic to?​​​​​​

Problem \(\PageIndex{7}\):

Find a non-trivial homomorphism from \(\mathbb{Z}_{10}\) to \(\mathbb{Z}_6\).

Problem \(\PageIndex{8}\)

Find all non-trivial homomorphisms from \(\mathbb{Z}_3\) to \(\mathbb{Z}_6\).

Problem \(\PageIndex{9}\)

Prove that the only homomorphism from \(D_3\) to \(\mathbb{Z}_3\) is the trivial homomorphism.

Problem \(\PageIndex{10}\)

Let \(F\) be the set of all functions from \(\mathbb{R}\) to \(\mathbb{R}\) and let \(D\) be the subset of differentiable functions on \(\mathbb{R}\). It turns out that \(F\) is a group under addition of functions and \(D\) is a subgroup of \(F\) (you do not need to prove this). Define \(\phi:D\to F\) via \(\phi(f)=f'\) (where \(f'\) is the derivative of \(f\)). Prove that \(\phi\) is a homomorphism. You may recall facts from calculus without proving them. Is \(\phi\) one-to-one? Onto?