6.1: Problems

1. (a) Establish all the abstract groups having an order \(2 \le N \le 6\). Compute typical products. Which groups are Abelian? Indicate at least two isomorphic realizations for each group.

   (b) Identify the subgroups. Which are invariant?

2. Write down the permutations of \(n = 3\) and \(n = 4\) objects. Arrange the result in a compact fashion. Consider at first the subgroup of even permutations (the alternating group). Make use of cycles.
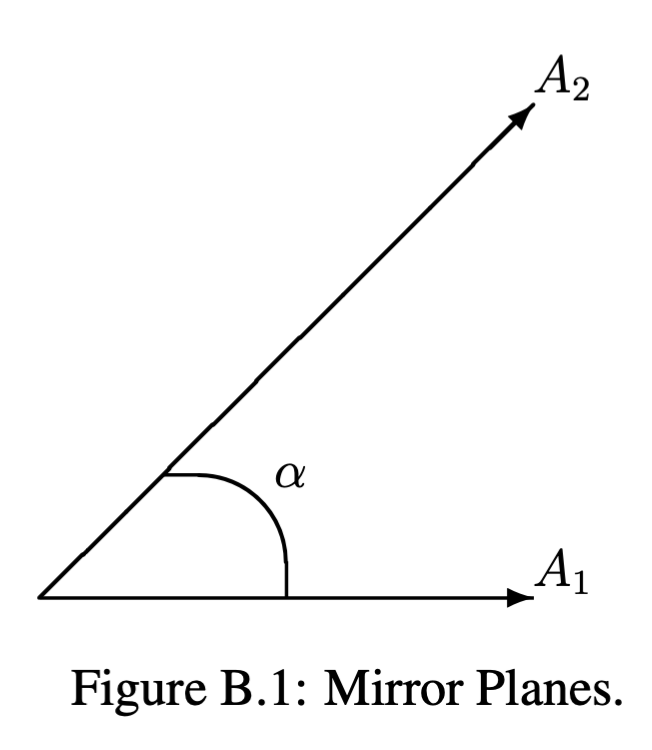
3. Find the joint effect of two mirror planes (see Figure B.1). Consider also parallel mirrors.

   

4. A spherical wave pulse diverges from the space-time point (0, 0, 0, 0) in the inertial frame \(\sum\). Consider a frame \(\sum'\) moving along the z direction with the velocity \(\beta = \tanh \mu\). The observer in \(\sum'\) sees also spherical wave fronts. However, the space-time points making up a surface \(r' = ct' = const\) do not look synchronous, hence spherical in \(\sum\). Show that the surfaces are ellipsoids of revolution with one common focus. Find the major and minor axes a, b, and the eccentricity in terms of \(r'\) and \(\beta\). Find also the lengths of the perihelion and the aphelion. Use polar coordinates.
5. Consider the composition of rotations in the \(\mathcal{SU}(2)\) formalism: \(U'' =U'U\) where \(U = l_{0} = -i \vec{l} \cdot \vec{\sigma}\), with

\[\begin{array}{cc} {l_{0} = \cos \frac{\phi}{2},}&{\vec{l} = \sin \frac{\phi}{2} \hat{u}} \nonumber \end{array}\]

(a) Express \(\{l_{0}'', \vec{l}''\}\) in terms of \(\{l_{0}', \vec{l}'\}\) and \(\{l_{0}, \vec{l}\}\).

(b) Refer to the Rodriues-Hamilton theorem (Figure 2.1) and obtain the cosine law of spher­ ical trigonometry.

(c) Obtain the sine law.

6. Check your general expressions by applying the special cases:

(a) \(U'' = UU = U^{2}\)

(b) \(\hat{u} = \frac{1}{\sqrt{3}} (1, 1, 1),}&{\phi = \frac{2 \pi}{3}\)

\(\hat{u} = \frac{1}{\sqrt{3}} (1, 0, 0),}&{\phi = \frac{\pi}{2}\)

Note that U and U' generate symmetry operations on the cube.

7. Consider the one-dimensional motion of a particle of rest mass m, under the influence of a force \(eE_{z}\). At \(t = 0\) the particle is at rest. Show that the trajectory is represented in the z, ct plane as a hyperbola and find the semi-diameter. Develop the analogy with the cyclotron problem as far as you can. Discuss the significance of the approximation

\[\begin{array}{c} {\gamma^{-1} = \sqrt{1-\beta^2} \simeq 1} \nonumber \end{array}\]

8. Consider an electromagnetic field

\[\begin{array}{c} {\vec{f} = \vec{E}+i \vec{B}} \nonumber \end{array}\]

in a small space-time region. The Lorentz invariant of the field is:

\[\begin{array}{c} {f^{2} = E^{2}-B^{2}+2i E \cdot B = I_{1}+i I_{2} = g^{2} \exp(2i \psi)} \nonumber \end{array}\]

(a) Consider the case \(f^{2} \ne 0\). In this case, a canonical frame exists in which \(E_{can} \parallel B_{can}\) and \(\zeta = B_{can}/E_{can}\), the pitch, is a real number (which could be 0 or \(\infty\)). Discuss the possible values of \(\zeta\) according to the signs of \(I_{1}\) and \(I_{2}\). Summarize your conclusions in a table such as that shown in Table B.1.

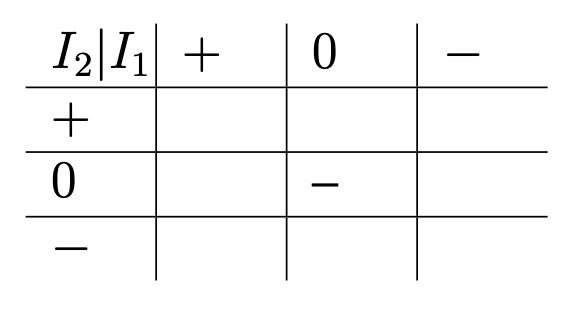
Table B.1: Table for Problem 8

(b) Express \(E_{can}, B_{can}, \zeta\) in terms of \(I_{1}, I_{2}\) and \(g, \psi\).

(c) Assume \(\zeta \ne 0, \infty\). Take \(\hat{x}\) along \(E_{can}\). Consider a passive Lorentz transformation in the \(\hat{z}\) direction, to a frame of velocity \(v(\beta = v/c = \tanh \mu)\) with respect to the canonical frame. Find \(\tan \theta E, \tan \theta B, \tan(\theta_{E}-\theta_{B})\) in terms of \(\beta, \zeta\) and also \(\mu, \psi\), where \(\theta_{E}\) and \(\theta_{B}\) are the angles by which the electric and magnetic fields rotate under the Lorentz transformation, as shown in Figure B.2.

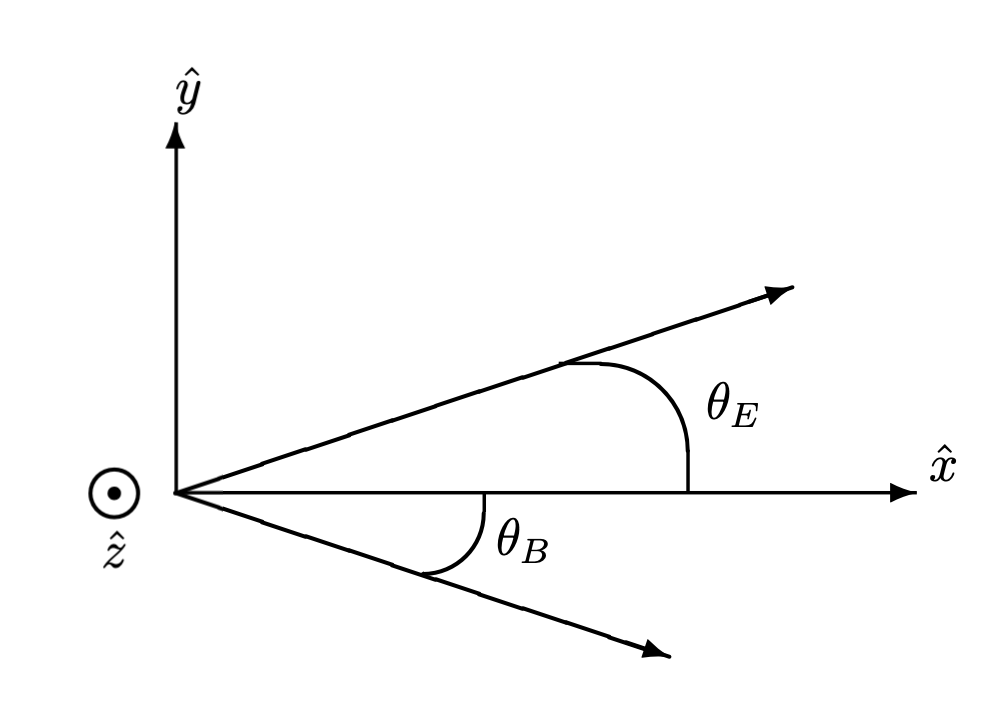
Figure B.2: Problem 8 coordinate frame and angles.

(d) Consider now the cases \(\zeta = 0; \zeta = \infty\). Take \(\hat{x}\) in the direction of the non-vanishing canonical field. Discuss the effect of a Lorentz transformation similar to that considered in (c). Give the ratio of the magnitudes of the electric and magnetic fields after the Lorentz transformation.

9. (a) Find the polar decomposition of the matrix

\[\begin{array}{c} {\begin{pmatrix} {1}&{\zeta}\\ {0}&{1} \end{pmatrix}} \nonumber \end{array}\]

Verify the relation (11b) on p. II-53. Consider the cases \(\delta = 1\) and \(\delta << 1\).

(b) Find

\[\begin{array}{c} {\mathcal{P}_{\hat{a}} (\vec{p} \cdot \vec{\sigma}) \mathcal{P}_{\hat{a}}} \nonumber \end{array}\]

where

\[\begin{array}{c} {\mathcal{P}_{\hat{a}} = \frac{1}{2} (1+\hat{a} \cdot \vec{\sigma})} \nonumber \end{array}\]

10. Verify Eq’s (23) - (26) on II-42, 43.

11. Show that the field matrix \(F = (\vec{E}+i \vec{B}) \cdot \vec{\sigma}\) can be derived from the matrix equivalent of the four-potential. What, if any, conditions are to be imposed on the latter?

12. (a) Express the reflection of a four-vector \(K = k_{0}1+\vec{k} \cdot \vec{\sigma}\) in a moving plane. The normal of the plane is \(\hat{a}\). Its velocity is \(v = v \hat{a}\) with \(v/c = \tanh \mu\). (Hint:transform to the rest frame of the mirror.)

(b) Show that the combination of two mirrors \(\vec{v}_{1} = v_{1} \hat{a}_{1}\), and \(\vec{v}_{2} = v_{2} \hat{a}_{2}\) yields a Lorentz transformation.

13. Verify the equivalence of Equations (4) and (5) in Section 4.2 by transforming each factor from space-to the body-frame.

14. Show that the relation

\[\begin{array}{c} {|\xi \rangle \langle \xi |= \frac{1}{2} (1+\hat{k} \cdot \vec{\sigma})} \end{array}\]

can be obtained through stereographic projection.

Hint: Project the sphere \(k_{1}^{2}+k_{2}^{2}+k_{3}^{2} = 1\) from the south pole to the equatorial plane interpreted as the complex z-plane. Express \(k_{1}, k_{2}, k_{3}\) in terms of \(z, z∗\) and set \(z = \xi_{1}/\xi_{0}\) with \(|\xi_{0}|^{2}+|\xi_{1}|^{2} = 1\).

15. Find the unitary matrix U that connects two given set of spinors with each other:

\[\begin{array}{c} {(| \eta \rangle, | \bar{\eta} \rangle) = (| \xi \rangle, | \bar{\xi} \rangle)U} \end{array}\]

Express first its elements, then its components in terms of \(\xi_{0}, \xi_{1}, \eta_{0}, \eta_{1}\).

16. The Pauli algebra can be considered as a generalization of elementary vector algebra and the knowledge of the latter is helpful in matrix manipulation.

However, one can approach the problem also from the converse point of view and derive the vector relations through matrix operations. Define

\[\begin{array}{ccc} {A= \vec{a} \cdot \vec{\sigma},}&{B = \vec{b} \cdot \vec{\sigma},}&{C = \vec{c} \cdot \vec{\sigma}} \nonumber \end{array}\]

and associate

\[\begin{array}{ccc} {\vec{a} \cdot \vec{b}}&{with}&{\frac{1}{2} \{A, B\} = \frac{1}{2} (AB+BA)} \end{array}\]

\[\begin{array}{ccc} {\vec{a} \times \vec{b}}&{with}&{\frac{1}{2i} \{A, B\} = \frac{1}{2i} (AB-BA)} \end{array}\]

Consider the Jacobi identity

\[\begin{array}{c} {[[A, B], C] + [[B, C], A] + [[C, A], B] = 0} \end{array}\]

and the condition for associativity:

\[\begin{array}{c} {A (BC)-(AB) C = 0} \end{array}\]

(Equation B.1.5 is easily verified for commutators. For its significance see [Hal74] .)

Translate Equation B.1.5 and B.1.6 by means of Equations B.1.3 and B.1.4, and obtain the familiar relations for triple vector products.

17. Give explicit spinorial expressions for the following polarization forms: \(| x \rangle\) (linear polariza­ tion along the x-axis); \(| \theta/2 \rangle\) (polarized at the angle \(\theta /2\) with the x-axis); \(| R \rangle\) (right circularly polarized).

(a) Use the \(\hat{\kappa} (\phi, \theta, \psi)\) scheme and assign \(\phi = \psi = \theta = 0\) to \(| x \rangle = (1, 0)\). Express \(| \theta/2 \rangle, | \theta/2 \rangle, | R \rangle, | \bar{R} \rangle\) in terms of \(| x \rangle\) and \(| \bar{x} \rangle\).

(b) Use the \(\hat{s}(\alpha, \beta, \gamma)\) scheme. Assign \(\beta = 0, \alpha = \gamma = \pi / 2\) to \(| R \rangle\). Express the above mentioned spinors in terms of \(| R \rangle\) and \(| \bar{R} \rangle\). Note that the results of (a) and (b) are consistent with each other.

18. Give the matrix representations of a quarter wave, plate, a half wave plate, a rotator and a plane polarizer in both the \(\hat{k}\) and the \(\hat{s}\) schemes.

19. (a) We know of an optical instrument only that it transforms \(| R \rangle\) into \(| \bar{R} \rangle\) and vice versa. Find the most general matrix operator consistent with this fact

(b) Sharpen this answer by using the additional information that the instrument passes a beam \(| x \rangle\) unchanged. What is the name of this device?

20. Consider an arbitrary Hermitian \(2 \times 2\) matrix: \(S = s_{0}+\vec{s} \cdot \vec{\sigma}\) with \(s_{0}^{2}-\vec{s}^{2} \ne 0\) in general.

(a) Show that it is possible to decompose S into a sum of two matrices with determinant zero. That is:

\[\begin{array}{c} {S = K'+K''} \nonumber \end{array}\]

where

\[\begin{array}{cc} {K' = k'_{0}+\vec{k}' \cdot \vec{\sigma}}&{k_{0}^{'2}-\vec{k}'^{2}} \nonumber \end{array}\]

\[\begin{array}{cc} {K'' = k''_{0}+\vec{k}'' \cdot \vec{\sigma}}&{k_{0}^{''2}-\vec{k}''^{2}} \nonumber \end{array}\]

(b) Show that if one imposes:

\[\begin{array}{c} {\vec{k}' = k' \hat{k}}\\ {\vec{k}'' = k'' \hat{k}}\\ {\vec{k}' and \vec{k}'' parallel} \nonumber \end{array}\]

the decomposition becomes unique. Find \(k_{0}', k_{0}'', k', k'', hat{k}\).

21. Consider an approximately monochromatic beam of unpolarized light, it has been suggested that such a beam be considered as a random sequence of elliptically polarized light, whereby the parameters of ellipticity \(\alpha, \beta\) vary slowly compared to \(1/\omega\) but fast compared to the time of observation (see [Hur45]). This author shows that the average ellipticity is given by the median value

\[\begin{array}{c} {(\frac{a_{2}}{a_{1}})_{m} = \tan(15^{\circ})} \nonumber \end{array}\]

This result can be obtained very simply. Assume that all representative points of the Poincare ́ sphere are equally probable. Consider the quantity:

\[\begin{array}{c} {S = \frac{2a_{1}a_{2}}{a_{1}^{2}+a_{2}^{2}}} \nonumber \end{array}\]

for an arbitrary point on the sphere.

Take the average of \(|S|\) over the Poincare ́ sphere, using the statistical assumption above.

Deduce the value

\[\begin{array}{c} {(\frac{a_{2}}{a_{1}})_{0}} \nonumber \end{array}\]

corresponding to \(\langle |S| \rangle\).