1.1: Symmetry
- Page ID
- 686
Groups arise in nature whenever we can find symmetry. For example, the human body has a lateral symmetry: if you imagine reversing left and right, most people would look more-or-less the same. (In fact, we see an example of this every time we look in a mirror.)
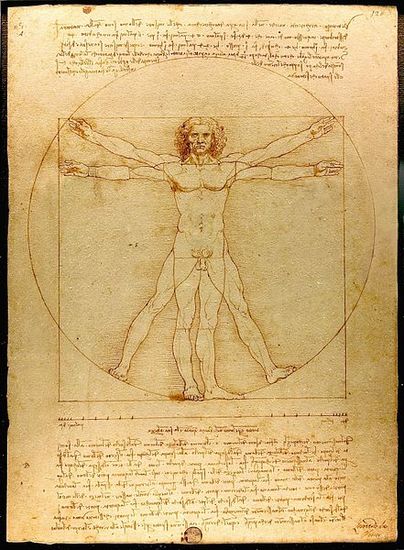
Figure 1: Da Vinci's famous sketch demonstrates lateral symmetry in the human body. (Source)
Another example is in the formation of crystals. In a crystal, the atomic structure arranges itself into a very symmetrical pattern, which you can see even with the unaided eye. The symmetry of the atomic structure means the atoms are packed very regularly, which leads to the nice shapes we see. In the late 1800's, mathematicians used group theory to classify all of the shapes of crystals that could ever exist in the world.

Figure 2: Twinned pyrite crystal. (Source)
Tiling patterns -- two-dimensional pictures that repeat in regular ways -- are also an example of symmetry. Many cultures have explored symmetry through tiling patterns, though the study of tiling was especially refined in the Islamic cultures during the middle ages. Bans on the depiction of human forms led Islamic artists to very deep explorations of abstract designs, with a strong emphasis on tiling. Group theory can also classify all of the possible regular tiling patterns, also known as tessellations, allowing us to verify that all of the possible tiling patterns were actually discovered by Islamic artists! There are many, many interesting tiling patterns out there: here's a place to start reading about them if you're interested.
A very deep example of symmetry occurs in our most fundamental assumptions in physics. A basic principle states that what matters in a physical system is the relationship between all of the objects, not their absolute position. This principle allows us to say that the physics we figure out on Earth should work the same on Mars. (Thus far in the history of the world, it's been a very useful assumption.) So if you move the entire system in any direction (or rotate it or reflect it), the system will not 'notice.' This invariance is also a kind of symmetry. Since you can move a physical system by any amount without changing it, the physical system has an infinite number of symmetries!
So what is a group? How can we create mathematics to encompass the study of symmetry? This is what we'll explore in this chapter.
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


