4.2: Subgroup Proofs and Lattices

Using Lemma \(4.1.1\) and the argument preceding it, we have the following.

Theorem \(\PageIndex{1}\)

A subset \(H\) of a group \(G\) is a subgroup of \(G\) if and only if

1. \(H\) is closed under \(G\)'s operation;
2. The identity element of \(G\) is in \(H\text{;}\) and
3. For each \(a\in H\text{,}\) \(a\)'s inverse in \(G\) is contained in \(H\text{.}\)

Example \(\PageIndex{1}\)

For each of the following, prove that the given subset \(H\) of group \(G\) is or is not a subgroup of \(G\text{.}\)

1. \(H=3\mathbb{Z}\text{,}\) \(G=\mathbb{Z}\text{.}\)
2. \(H=\{0,1,2,3\}\text{,}\) \(G=\mathbb{Z}_6\text{;}\)
3. \(H=\mathbb{R}^*\text{,}\) \(G=\mathbb{R}\text{;}\)
4. \(H=\{(0,x,y,z):x,y,z\in \mathbb{R}\}\text{,}\) \(G=\mathbb{R}^4\text{.}\)

Example \(\PageIndex{2}\)

Generalizing Part 1 of the above theorem, we have \(n\mathbb{Z}\leq \mathbb{Z}\) for every \(n\in \mathbb{Z}^+\text{.}\)

The proof of this is left as an exercise for the reader.

Example \(\PageIndex{3}\)

Consider the group \(\langle F,+\rangle\text{,}\) where \(F\) is the set of all functions from \(\mathbb{R}\) to \(\mathbb{R}\) and \(+\) is pointwise addition. Which of the following are subgroups of \(F\text{?}\)

1. \(H=\{f\in F: f(5)=0\}\text{;}\)

2. \(K=\{f\in F: f \text{ is continuous} \}\text{;}\)

3. \(L=\{f\in F: f \text{ is differentiable} \}\text{.}\)

Are any of \(H\text{,}\) \(K\text{,}\) and \(L\) subgroups of one another?

In fact, we can narrow down the number of facts we need to check to prove a subset \(H\subseteq G\) is a subgroup of \(G\) to only two.

Theorem \(\PageIndex{2}\): Two-Step Subgroup Test

Let \(G\) be a group and \(H\subseteq G\text{.}\) Then \(H\) is a subgroup of \(G\) if

1. \(H\neq \emptyset\text{;}\) and
2. For each \(a,b\in H\text{,}\) \(ab^{-1}\in H\text{.}\)

Proof

Assume that the above two properties hold. Since \(H≠∅\), there exists an \(x∈G\) such that \(x∈H\). Then \(e_G=xx^{−1}\) is in \(H\), by the second property. Next, for every \(a∈H\) we have \(a^{−1}=e_Ga^{−1}∈H\) (again by the second property). Finally, if \(a,b∈H\) then we've already shown \(b^{−1}∈H\); so \(ab=a(b^{−1})^{−1}∈H\), yet again by the second property. Thus, \(H≤G\).

Example \(\PageIndex{4}\)

1. Use the Two-Step Subgroup Test to prove that \(3\mathbb{Z}\) is a subgroup of \(\mathbb{Z}\text{.}\)
2. Use the Two-Step Subgroup Test to prove that \(SL(n,\mathbb{R})\) is a subgroup of \(GL(n,\mathbb{R})\text{.}\)

Assume that the above two properties hold. Since \(H\neq \emptyset\text{,}\) there exists an \(x\in G\) such that \(x\in H\text{.}\) Then \(e_G=xx^{-1}\) is in \(H\text{,}\) by the second property. Next, for every \(a\in H\) we have \(a^{-1}=e_Ga^{-1}\in H\) (again by the second property). Finally, if \(a,b\in H\) then we've already shown \(b^{-1}\in H\text{;}\) so \(ab=a(b^{-1})^{-1}\in H\text{,}\) yet again by the second property. Thus, \(H\leq G\text{.}\)​​​​​​It is straightforward to prove the following theorem.

Theorem \(\PageIndex{3}\)

If \(H\) is a subgroup of a group \(G\) and \(K\) is a subset of \(H\text{,}\) then \(K\) is a subgroup of \(H\) if and only if it's a subgroup of \(G\text{.}\)

It can be useful to look at how subgroups of a group relate to one another. One way of doing this is to consider subgroup lattices (also known as subgroup diagrams). To draw a subgroup lattice for a group \(G\text{,}\) we list all the subgroups of \(G\text{,}\) writing a subgroup \(K\) below a subgroup \(H\text{,}\) and connecting them with a line, if \(K\) is a subgroup of \(H\) and there is no proper subgroup \(L\) of \(H\) that contains \(K\) as a proper subgroup.

Example \(\PageIndex{5}\)

Consider the group \(\mathbb{Z}_8\text{.}\) We will see later that the subgroups of \(\mathbb{Z}_8\) are \(\{0\}\text{,}\) \(\{0,2,4,6\}\text{,}\) \(\{0,4\}\) and \(\mathbb{Z}_8\) itself. So \(\mathbb{Z}_8\) has the following subgroup lattice.

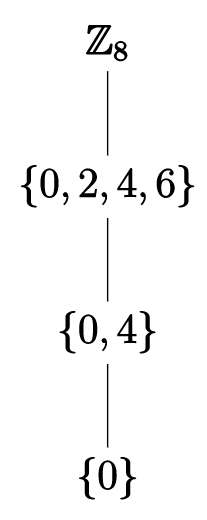
Example \(\PageIndex{6}\)

Referring to Example \(4.2.3\), draw the portion of the subgroup lattice for \(F\) that shows the relationships between itself and its proper subgroups \(H\text{,}\) \(K\text{,}\) and \(L\text{.}\)

Example \(\PageIndex{7}\)

Indicate the subgroup relationships between the following groups: \(\mathbb{Z}\text{,}\) \(12\mathbb{Z}\text{,}\) \(\mathbb{Q}^+\text{,}\) \(\mathbb{R}\text{,}\) \(6\mathbb{Z}\text{,}\) \(\mathbb{R}^+\text{,}\) \(3\mathbb{Z}\text{,}\) \(G=\langle \{\pi^n:n\in \mathbb{Z}\},\cdot\,\rangle\) and \(J=\langle \{6^n:n\in \mathbb{Z}\},\cdot\,\rangle .\)

We end with a theorem about homomorphisms and subgroups that leads us to another group invariant.

Theorem \(\PageIndex{4}\)

Let \(G\) and \(G'\) be groups, let \(\phi\) a homomorphism from \(G\) to \(G'\text{,}\) and let \(H\) a subgroup of \(G\text{.}\) Then \(\phi(H)\) is a subgroup of \(G'\text{.}\)

Proof

The proof is left as an exercise for the reader.

Corollary \(\PageIndex{1}\)

The probabilities assigned to events by a distribution function on a sample space are given by.

Proof

If \(G\simeq G'\) and \(G\) contains exactly \(n\) subgroups (\(n\in \mathbb{Z}^+\)), then so does \(G'\text{.}\)

This is another way of, for instance, distinguishing between the groups \(\mathbb{Z}_4\) and the Klein 4-group \(\mathbb{Z}_2^2\text{.}\)

Example \(\PageIndex{8}\)

By inspection, \(\mathbb{Z}_4\) and \(\mathbb{Z}_2^2\) have, respectively, the following subgroup lattices.

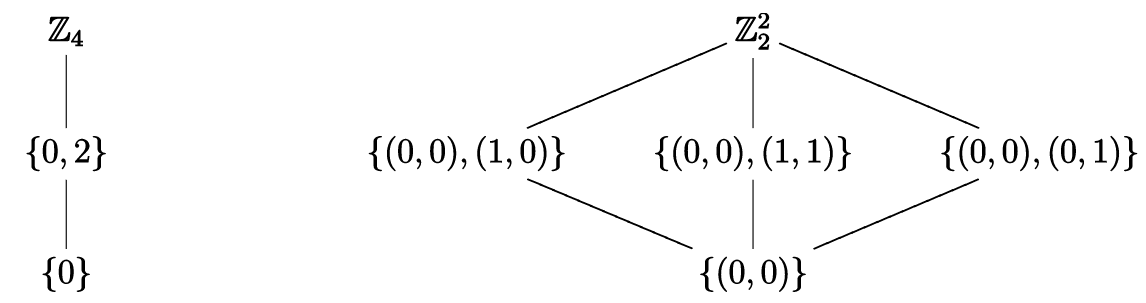
Since \(\mathbb{Z}_4\) contains exactly \(3\) subgroups and \(\mathbb{Z}_2^2\) exactly \(5\), we have that \(\mathbb{Z}_4\not\simeq \mathbb{Z}_2^2\text{.}\)