9.1: The First Isomorphism Theorem

A very powerful theorem, called the First Isomorphism Theorem, lets us in many cases identify factor groups (up to isomorphism) in a very slick way. Kernels will play an extremely important role in this. We therefore first provide some theorems relating to kernels.

Theorem \(\PageIndex{1}\)

Let \(G\) and \(G'\) be groups, let \(\phi\) be a homomorphism from \(G\) to \(G'\text{,}\) and let \(K=\text{Ker}\; \phi\text{.}\) Then for \(a,b\in G\text{,}\) \(aK=bK\) if and only if \(\phi(a)=\phi(b)\text{.}\)

Proof

Let \(a,b∈G\). Then

\( \begin{array} &ϕ(a)=ϕ(b)&⇔ϕ(b)^{−1}ϕ(a)=e_{G′}\\&⇔ϕ(b^{−1}a)=e_{G′}\\&⇔b^{−1}a∈K\\&⇔a∈bK\\&⇔aK=bK, \end{array}\)

as desired.

Corollary \(\PageIndex{1}\)

Let \(\phi\) be a homomorphism from group \(G\) to group \(G'\text{.}\) Then \(\phi\) is one-to-one (hence a monomorphism) if and only if \(\text{Ker} \phi=\{e_G\}\text{.}\)

Proof

Clearly, if \(ϕ\) is one-to-one then \(\text{Ker}⁡ϕ=\{e_G\}\). Conversely, assume \(\text{Ker}ϕ=\{e_G\}\).

If \(a,b∈G\) with \(ϕ(a)=ϕ(b)\), then by the above theorem, \(a\text{Ker}⁡ϕ=b\text{Ker}⁡ϕ\). But \(a\text{Ker}⁡ϕ=a\{e_G\}=\{a\}\) and \(b\text{Ker}⁡ϕ=b\{e_G\}=\{b\}\). Thus, \(a=b\), and we see that \(ϕ\) is one-to-one.

Clearly, if \(\phi\) is one-to-one then \(\Ker \phi=\{e_G\}\text{.}\) Conversely, assume \(\Ker \phi=\{e_G\}\text{.}\) If \(a,b\in G\) with \(\phi(a)=\phi(b)\text{,}\) then by the above theorem, \(a\Ker \phi=b\Ker \phi\text{.}\) But \(a\Ker \phi=a\{e_G\}=\{a\}\) and \(b\Ker \phi=b\{e_G\}=\{b\}\text{.}\) Thus, \(a=b\text{,}\) and we see that \(\phi\) is one-to-one.

We now prove a theorem that provides the meat and potatoes of the First Isomorphism Theorem.

Theorem \(\PageIndex{2}\): Factorization Theorem

Let \(G\) and \(G'\) be groups, let \(\phi\) be a homomorphism from \(G\) to \(G'\text{,}\) let \(K=\text{Ker} \phi\text{,}\) let \(N\) be a normal subgroup of \(G\) with \(N\subseteq K\text{,}\) and let \(\Psi\) be the canonical epimorphism from \(G\) to \(G/N\text{.}\) Then the map \(\overline{\phi}: G/N \to G'\) defined by \(\overline{\phi}(aN)=\phi(a)\) is a well-defined homomorphism, with \(\overline{\phi} \circ \Psi=\phi\text{.}\)

We summarize this in the following picture:

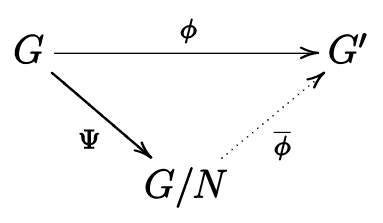
Proof

We define \(\overline{\phi}:G/N→G′\), as indicated above, by \(\overline{\phi}(aN)=ϕ(a)\) for every \(aN∈G/N\). Since \(\overline{\phi}\) is defined using coset representatives, we must first show that \(\overline{\phi}\) is well-defined. So let \(aN=bN∈G/N\). Then \(\overline{\phi}(aN)=ϕ(a)\) and \(\overline{\phi}(bN)=ϕ(b)\), so we must show that \(ϕ(a)=ϕ(b)\). Since \(aN=bN\) and \(N⊆K\), we have that \(aK=bK\) by Statement 6 of Theorem \(7.2.3\); thus \(ϕ(a)=ϕ(b)\) (using Theorem \(9.1.1\)). So \(\overline{\phi}\) is well-defined.

Next, we show that \(\overline{\phi}\) is a homomorphism. Let a\(aN,bN∈G/N\). Then

\(\overline{\phi}((aN)(bN))= \overline{\phi}(abN)=ϕ(ab)=ϕ(a)ϕ(b)=\overline{\phi}(aN)\overline{\phi}(bN)\).

Finally, for every \(a∈G\),

\((\overline{\phi} \circ Ψ)(a)=\overline{\phi}(Ψ(a))=\overline{\phi}(aN)=ϕ(a)\);

so \(\overline{\phi} \circ Ψ=ϕ\), as desired.

Note that the above theorem does not state that \(\overline{\phi}\) is a monomorphism or an epimorphism. This is because in general it may be neither! We do have the following theorem:

Theorem \(\PageIndex{3}\)

Let \(G\text{,}\) \(G'\text{,}\) \(\phi\text{,}\) \(N\text{,}\) and \(\overline{\phi}\) be as defined in the Factorization Theorem. Then

1. \(\overline{\phi}\) is onto (an epimorphism) if and only if \(\phi\) is onto (an epimorphism); and
2. \(\overline{\phi}\) is one-to-one (a monomorphism) if and only if \(N=\text{Ker} \phi\text{.}\)

Proof

This is clear, since \(\overline{\phi}(G/N)=ϕ(G)\).

By Corollary \(9.1.1\), \(\overline{\phi}\) is one-to-one if and only if \(\text{Ker}\overline{\phi}=\{N\}\). But

\(\begin{array}& \text{Ker}\overline{\phi}&=\{aN∈G/N:\overline{\phi}(aN)=e_{G′}\} \\&=\{aN∈G/N:ϕ(a)=e_{G′}\} \\&=\{aN∈G/N:a∈\text{Ker}ϕ\}. \end{array}\)

So \(\text{Ker}\overline{\phi}⁡=\{N\}\) if and only if

\(\{aN∈G/N:a∈\text{Ker}ϕ\}=\{N\}\),

in other words if and only if \(aN=N\) for all \(a∈\text{Ker}⁡ϕ\). But

\(\begin{array} &&3&&aN=N   &\text{ for all } a∈\text{Ker}ϕ \\&& ⇔&a∈N   &\text{ for all } a∈\text{Ker}ϕ \\&&⇔&\text{Ker}ϕ⊆N \\&&⇔&\text{Ker}ϕ=N, \end{array}\)

since we are given that \(N⊆\text{Ker}⁡ϕ\). Thus, \(\overline{\phi}\) is one-to-one if and only if \(N=\text{Ker}⁡ϕ\), as desired.

We are now ready to state the all-important First Isomorphism Theorem, which follows directly from the Factorization Theorem and Theorem \(9.1.3\).

Theorem \(\PageIndex{4}\): First Isomorphism Theorem

Let \(G\) and \(G'\) be groups, with homomorphism \(\phi:G \rightarrow G'\text{.}\) Let \(K=\text{Ker} \phi\text{.}\) Then \(G/K \simeq \phi(G)\text{.}\) In particular, if \(\phi\) is onto, then \(G/K\simeq G'\text{.}\)

So to prove that a factor group \(G/N\) is isomorphic to a group \(G'\text{,}\) it suffices to show there exists an epimorphism from \(G\) to \(G'\) that has \(N\) as its kernel.

Example \(\PageIndex{1}\)

Letting \(n\in \mathbb{Z}^+\text{,}\) let's identify a familiar group to which \(GL(n,\mathbb{R})/SL(n,\mathbb{R})\) is isomorphic. As in Example \(8.2.3\), the map \(\phi:GL(n,\mathbb{R})\to \mathbb{R}^*\) defined by \(\phi(A)\) is a homomorphism with kernel \(SL(n,\mathbb{R})\text{.}\) Moreover, \(Phi\) clearly maps onto \(\mathbb{R}^*\text{:}\) indeed, given \(\lambda \in \mathbb{R}^*\text{,}\) the diagonal matrix having \(\lambda\) in the uppermost left position and \(1\)'s elsewhere down the diagonal gets sent to \(\lambda\) by \(\phi\text{.}\) So by the First Isomorphism Theorem, we have \(GL(n,\mathbb{R})/SL(n,\mathbb{R}) \simeq \mathbb{R}^*\text{.}\)

Example \(\PageIndex{2}\)

Let \(G=S_3\times \mathbb{Z}_{52}\) and let \(N=S_3 \times \{0\}\subseteq G\text{.}\) It is straightforward to show that \(N\) is normal in \(G\text{.}\) What is the structure of \(G/N\text{?}\) Well, define \(\phi:G\to \mathbb{Z}_{52}\) by \(\phi((\sigma, a))=a\text{.}\) Then \(\phi\) is clearly an epimorphism and \(\text{Ker} \phi=\{(\sigma,a)\in G\,:a=0\}=N\text{.}\) So \(G/N\) is isomorphic to \(\mathbb{Z}_{52}\text{.}\)

Generalizing the above example, we have the following theorem, whose proof we leave to the reader.

Theorem \(\PageIndex{5}\)

Let \(G=G_1\times G_2 \times \cdots \times G_k\) (where \(k\in \mathbb{Z}^+\)) and let \(N_i\) be a normal subgroup of \(G_i\) for each \(i=1,2,\ldots, k\text{.}\) Then \(N=N_1 \times N_2 \times \cdots \times N_k\) is a normal subgroup of \(G\text{,}\) with \(G/N \simeq G_1/N_1 \times G_2/N_2 \cdots \times G_k/N_k.\)

We provide one more cool example of using the First Isomorphism Theorem. Clearly, since \(\mathbb{R}\) is abelian, \(\mathbb{Z}\) is a normal subgroup of \(\mathbb{R}\text{.}\) What is the structure of \(\mathbb{R}/\mathbb{Z}\text{?}\) Well, in modding \(\mathbb{R}\) out by \(\mathbb{Z}\) we have essentially identified together all real numbers that are an integer distance apart. So we can think of the canonical epimorphism from \(\mathbb{R}\) to \(\mathbb{R}/\mathbb{Z}\) as wrapping up \(\mathbb{R}\) like a garden hose! Thus, one might guess that \(\mathbb{R}/\mathbb{Z}\) has some circle-like structure—but if we want to think of it as a group, we have to figure out what the group structure on such a “circle” would be!

We leave, for a moment, our group \(\mathbb{R}/\mathbb{Z}\text{,}\) and look at how we can consider a circle to be a group.

Recall that for every \(\theta \in \mathbb{R}\text{,}\) \(e^{i\theta}\) is defined to be \(\cos \theta + i\sin \theta\text{.}\) It is clear then that the set \(S^1=\{e^{i\theta} \,:\, \theta\in \mathbb{R}\}\) is the unit circle in the complex plane.

Remark

Note that if \(\theta_1, \theta_2\in \mathbb{R}\text{,}\) then \(e^{i\theta_1}=e^{i\theta_2}\) if and only if \(\theta_1-\theta_2 \in 2\pi \mathbb{Z}\text{.}\)

Theorem \(\PageIndex{6}\)

\(S^1\) is a group under the multiplication \(e^{i\theta_1}e^{i\theta_2}=e^{i(\theta_1+\theta_2)}\text{.}\)

Proof

The tricky part is showing that the operation is well-defined. Suppose \(θ_1,θ_2,t_1\), and \(t_2\) are in \(R\), with \(e^{iθ_1}=e^{it_1}\) and \(e^{iθ_2}=e^{it_2}\). We want to show that

\(e^{iθ_1}e^{iθ_2}=e^{it_1}e^{it_2}\),

i.e., that

\(e^{i(θ_1+θ_2)}=e^{i(t_1+t_2)}\).

Now, \(e^{iθ_1}=e^{it_1}\) and \(e^{iθ_2}=e^{it_2}\) imply that \(θ_1−t_1=2πm\) and \(θ_2−t_2=2πn\) for some \(m\) and \(n\) in \(\mathbb{Z}\); hence,

\(θ_1+θ_2−(t_1+t_2)=2π(m+n)∈2π\mathbb{Z}\).

Thus, \(e^{i(θ_1+θ_2)}=e^{i(t_1+t_2)}\), so our operation is well-defined.

Since products of elements in \(S^1\) are in \(S^1\), we have that \(S^1\) is a binary structure; moreover, associativity of the operation in \(S^1\) follows from the associativity of addition in \(\mathbb{R}\). Moreover, \(e^{i0}=1\) clearly acts as an identity element in \(S^1\), and if \(e^{iθ}∈S^1\), then \(e^{iθ}\) has inverse \(e^{i(−θ)}∈S^1\). So \(S^1\) is a group under the described operation.

The tricky part is showing that the operation is well-defined. Suppose \(\theta_1, \theta_2, t_1\text{,}\) and \(t_2\) are in \(\R\text{,}\) with \(e^{i\theta_1}=e^{it_1}\) and \(e^{i\theta_2}=e^{it_2}\text{.}\) We want to show that

\begin{equation*} e^{i\theta_1}e^{i\theta_2}=e^{it_1}e^{it_2}, \end{equation*}

i.e., that

\begin{equation*} e^{i(\theta_1+\theta_2)}=e^{i(t_1+t_2)}. \end{equation*}

Now, \(e^{i\theta_1}=e^{it_1}\) and \(e^{i\theta_2}=e^{it_2}\) imply that \(\theta_1 -t_1 = 2\pi m\) and \(\theta_2-t_2 = 2\pi n\) for some \(m\) and \(n\) in \(\Z\text{;}\) hence,

\begin{equation*} \theta_1+\theta_2-(t_1+t_2)= 2\pi(m+n) \in 2\pi\Z. \end{equation*}

Thus, \(e^{i(\theta_1+\theta_2)}=e^{i(t_1+t_2)}\text{,}\) so our operation is well-defined.

Since products of elements in \(S^1\) are in \(S^1\text{,}\) we have that \(S^1\) is a binary structure; moreover, associativity of the operation in \(S^1\) follows from the associativity of addition in \(\R\text{.}\) Moreover, \(e^{i0}=1\) clearly acts as an identity element in \(S^1\text{,}\) and if \(e^{i\theta}\in S^1\text{,}\) then \(e^{i\theta}\) has inverse \(e^{i(-\theta)} \in S^1\text{.}\) So \(S^1\) is a group under the described operation.

Beautifully, it turns out that our group \(\mathbb{R}/\mathbb{Z}\) is isomorphic to \(S^1\text{.}\)

Theorem \(\PageIndex{7}\)

\(\mathbb{R}/\mathbb{Z} \simeq S^1\text{.}\)

Proof

We will define an epimorphism \(ϕ\) from \(\mathbb{R}\) to \(S^1\) with \(\text{Ker}ϕ=\mathbb{Z}\); then we'll have \(\mathbb{R}/\mathbb{Z}≃S^1\), by the First Isomorphism Theorem.

Define \(ϕ:\mathbb{R}→S^1\) by \(ϕ(r)=e^{i2πr}\). We have that \(ϕ\) is a homomorphism, since for every \(r,s∈\mathbb{R}\), we have

\(ϕ(r+s)=e^{i2π(r+s)}=e^{i2πr+i2πs}=e^{i2πr}e^{i2πs}=ϕ(r)ϕ(s)\).

Moreover, \(ϕ\) is clearly onto, since if \(e^{iθ}∈S^1\), then

\(e^{iθ}=e^{i2π(θ2π)}=ϕ(θ2π)\).

Finally, \(\text{Ker}⁡ϕ=\mathbb{Z}\): indeed,

\(\begin{array}& r∈\text{Ker}⁡ϕ&⇔ϕ(r)=1\\&⇔e^{i2πr}=1\\&⇔\cos⁡2πr+i\sin⁡2πr=1\\&⇔\cos⁡2πr=1 \text{ and } \sin⁡2πr=0\\&⇔r∈\mathbb{Z}. \end{array}\)

Thus, \(\text{Ker}⁡ϕ=\mathbb{Z}\), and hence \(\mathbb{R}/\mathbb{Z}≃S^1\), as desired.

We will define an epimorphism \(\phi\) from \(\R\) to \(S^1\) with \(\Ker \phi=\Z\text{;}\) then we'll have \(\R/\Z \simeq S^1\text{,}\) by the First Isomorphism Theorem.

Define \(\phi:\R \to S^1\) by \(\phi(r)=e^{i2\pi r}\text{.}\) We have that \(\phi\) is a homomorphism, since for every \(r,s\in \R\text{,}\) we have

\begin{equation*} \phi(r+s)=e^{i2\pi (r+s)}=e^{i2\pi r+i2\pi s}=e^{i2\pi r}e^{i2\pi s}=\phi(r)\phi(s). \end{equation*}

Moreover, \(\phi\) is clearly onto, since if \(e^{i\theta}\in S^1\text{,}\) then

\begin{equation*} e^{i\theta}=e^{i2\pi\left(\frac{\theta}{2\pi}\right)}=\phi\left(\frac{\theta}{2\pi}\right). \end{equation*}

Finally, \(\Ker\phi=\Z\text{:}\) indeed,

\begin{align*} r\in \Ker\phi \amp \Leftrightarrow \phi(r)=1\\ \amp \Leftrightarrow e^{i2\pi r}=1\\ \amp \Leftrightarrow \cos 2\pi r + i\sin 2\pi r=1\\ \amp \Leftrightarrow \cos 2\pi r = 1 \text{ and } \sin 2\pi r = 0\\ \amp \Leftrightarrow r\in \Z. \end{align*}

Thus, \(\Ker \phi = \Z\text{,}\) and hence \(\R/\Z\simeq S^1\text{,}\) as desired.