Solutions to Exercises

1. Yes/No. For each of the following, write Y if the object described is a well-defined set; otherwise, write N. You do NOT need to provide explanations or show work for this problem.

$\{z \in \mathbb{C} \,:\, |z|=1\}$
$\{\epsilon \in \mathbb{R}^+\,:\, \epsilon \mbox{ is sufficiently small} \}$
$\{q\in \mathbb{Q} \,:\, q \mbox{ can be written with denominator } 4\}$
$\{n \in \mathbb{Z}\,:\, n^2 \lt 0\}$

Solution

Y
N
Y (it's $\mathbb{Q}$)
Y (it's $∅$)

2. List the elements in the following sets, writing your answers as sets.

Example: $\{z\in \mathbb{C}\,:\,z^4=1\}$ Solution: $\{\pm 1, \pm i\}$

$\{z\in \mathbb{R}\,:\, z^2=5\}$
$\{m \in \mathbb{Z}\,:\, mn=50 \mbox{ for some } n\in \mathbb{Z}\}$
$\{a,b,c\}\times \{1,d\}$
$P(\{a,b,c\})$

Solution

$\{±√5\}$
$\{±50,±25,±10,±5,±2,±1\}$
$\{(a,1),(a,d),(b,1),(b,d),(c,1),(c,d)\}$
$\{∅,\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\},\{a,b,c\}\}$

3. Let $S$ be a set with cardinality $n\in \mathbb{N}\text{.}$ Use the cardinalities of $P(\{a,b\})$ and $P(\{a,b,c\})$ to make a conjecture about the cardinality of $P(S)\text{.}$ You do not need to prove that your conjecture is correct (but you should try to ensure it is correct).

Solution

$|P(\{a,b\})|=4=2^2$ and $|P(\{a,b,c\})|=8=2^3$; we may conjecture that when $|S|=n$, $|P(S)|=2^n$.

4. Let $f: \mathbb{Z}^2 \to \mathbb{R}$ be defined by $f(a,b)=ab\text{.}$ (Note: technically, we should write $f((a,b))\text{,}$ not $f(a,b)\text{,}$ since $f$ is being applied to an ordered pair, but this is one of those cases in which mathematicians abuse notation in the interest of concision.)

What are $f$'s domain, codomain, and range?
Prove or disprove each of the following statements. (Your proofs do not need to be long to be correct!)
1. $f$ is onto;
2. $f$ is 1-1;
3. $f$ is a bijection. (You may refer to parts (i) and (ii) for this part.)
Find the images of the element $(6,-2)$ and of the set $\mathbb{Z}^- \times \mathbb{Z}^-$ under $f\text{.}$ (Remember that the image of an element is an element, and the image of a set is a set.)
Find the preimage of $\{2,3\}$ under $f\text{.}$ (Remember that the preimage of a set is a set.)

Solution

$f$'s domain, codomain, and range are, respectively, $\mathbb{Z}^2$, $\mathbb{R}$, and $\mathbb{Z}$.
1. $f$ is not onto, since, for instance, $1/2∈\mathbb{R}−\mathbb{Z}$.
2. $f$ is not 1-1: for instance, $f(−2,2)=−4=f(2,−2)$.
3. $f$ is not a bijection since it's not 1-1. (It would be equally valid to answer that it's not a bijection since it's not onto, or that it's not a bijection since it's neither 1-1 nor onto.)
$f(6,−2)=−12$ and $f(\mathbb{Z}^− \times \mathbb{Z}^−)=\mathbb{Z}^+$.
$\begin{array}& f←({2,3})&=\{(a,b)∈\mathbb{Z} \times \mathbb{Z}:f(a,b)∈\{2,3\}\}\\&=\{(a,b)∈\mathbb{Z} \times \mathbb{Z}:ab=2 \text{ or } ab=3\} \end{array}$
which is the set
$\{(1,2),(2,1),(−1,−2),(−2,−1),(1,3),(3,1),(−1,−3),(−3,−1)\}$.

5. Let $S\text{,}$ $T\text{,}$ and $U$ be sets, and let $f: S\to T$ and $g: T\to U$ be onto. Prove that $g \circ f$ is onto.

Solution

Let $u∈U$. We want to show there is an element of $S$ that gets mapped to uu by $g \circ f$.

Since $g:T→U$ is onto, there is an element $t∈T$ such that $g(t)=u$; next, since $f:S→T$ is onto, there is an element $s∈S$ such that $f(s)=t$.

Then $(g \circ f)(s)=g(f(s))=g(t)=u$. Thus, $g \circ f$ is onto.

6. Let $A $ and $B$ be sets with $|A|=m\lt \infty$ and $|B|=n\lt \infty\text{.}$ Prove that $|A\times B|=mn\text{.}$

Solution

We can list the elements of $A$ and $B$ as so:

$A=\{a_1,a_2,…,a_m\}$ and $B=\{b_1,b_2,…,b_n\}$.

Consider the table

$\begin{array}& (a_1,b_1)&(a_1,b_2)& \ldots &(a_1,b_n) \\ (a_2,b_1)&(a_2,b_2)& \ldots &(a_2,b_n) \\ \vdots&\vdots& \ddots &\vdots \\ (a_m,b_1)&(a_m,b_2)& \ldots &(a_m,b_n) \\ \end{array}$

Clearly this table contains $mn$ elements, and contains each element of $A \times B$ exactly once. Therefore, $|A \times B|=mn$.

Exercise 2.2 (Part I)

1. For each of the following, write Y if the given “operation” is a well-defined binary operation on the given set; otherwise, write N. In each case in which it isn't a well-defined binary operation on the set, provide a brief explanation. You do not need to prove or explain anything in the cases in which it is a binary operation.

$+$ on $\mathbb{C}^*$
$*$ on $\mathbb{R}^+$ defined by $x*y=\log_x y$
$*$ on $\mathbb{M}_2(\mathbb{R})$ defined by $A*B=AB^{-1}$
$*$ on $\mathbb{Q}^*$ defined by $z*w=z/w$

Solution

N; for instance, $1,−1∈\mathbb{C}^∗$, but $1+(−1)=0∉\mathbb{C}^∗$.
N; for instance, $10∗1=\log_{10}⁡0.1=−1∉\mathbb{R}^+$.
N; for instance, the zero matrix, $0$, in $\mathbb{M}^2(\mathbb{R})$ is not invertible, so $A∗0$ is undefined for every $A∈\mathbb{M}2(\mathbb{R})$.
Y

2. Define $*$ on $\mathbb{Q}$ by $p*q=pq+1\text{.}$ Prove or disprove that $*$ is (a) commutative; (b) associative.

Solution

Let $p,q∈\mathbb{Q}$. Then $p∗q=pq+1=qp+1$ (since multiplication is commutative on $\mathbb{Q}$), which equals $q∗p$. So $∗$ is commutative.
$∗$ is not associative: for instance, $1,2,3∈\mathbb{Q}$ and $1∗(2∗3)=1∗7=8$, while $(1∗2)∗3=3∗3=10≠8$.

3. Prove that matrix multiplication is not commutative on $\mathbb{M}_2(\mathbb{R})\text{.}$

Solution

Let $A= \begin{bmatrix} 1 & 0 \\ 0 & 0\end{bmatrix}$ and $B=\begin{bmatrix} 0 & 1 \\0 & 0\end{bmatrix}$ in $\mathbb{M}^2(\mathbb{R})$. Then $AB=B$ while $BA$ is the zero matrix. Since $AB≠BA$, matrix multiplication isn't commutative on $\mathbb{M}^2(\mathbb{R})$.

4. Prove or disprove each of the following statements.

The set $2\mathbb{Z}=\{2x\;:\;x\in \mathbb{Z}$ is closed under addition in $\mathbb{Z}\text{.}$
The set $S=\{1,2,3\}$ is closed under multiplication in $\mathbb{R}\text{.}$
The set
\begin{equation*} U=\left\{ \begin{bmatrix} a & b\\ 0 & c \end{bmatrix}\,:\,a,b,c\in \mathbb{R}\right\} \end{equation*}
is closed under multiplication in $\mathbb{M}_2(\mathbb{R})\text{.}$ (Recall that $U$ is the set of upper-triangular matrices in $\mathbb{M}_2(\mathbb{R})\text{.}$)

Solution

Let $x,y∈2\mathbb{Z}$. Then there exist $a,b∈\mathbb{Z}$ such that $x=2a$ and $y=2b$. Then
$x+y=2a+2b=2(a+b)∈2\mathbb{Z}$.
So $2\mathbb{Z}$ is closed under addition.
Since, for instance, $2,3∈S$ but $2(3)=6∉S$, $S$ isn't closed under multiplication.
Let $A = \begin{bmatrix} a & b\\ 0 & c \end{bmatrix}$ and $B=\begin{bmatrix} \alpha & \beta \\ 0 & \gamma \end{bmatrix}$ in $U$. Then
$AB = \begin{bmatrix} a & b\\ 0 & c \end{bmatrix}\begin{bmatrix} \alpha & \beta \\ 0 & \gamma \end{bmatrix} = \begin{bmatrix} a\alpha & a\beta + b\gamma \\ 0 & c\gamma \end{bmatrix} ∈U$
So $U$ is closed under matrix multiplication.

5. Let $*$ be an associative and commutative binary operation on a set $S\text{.}$ An element $u\in S$ is said to be an idempotent in $S$ if $u*u=u\text{.}$ Let $H$ be the set of all idempotents in $S\text{.}$ Prove that $H$ is closed under $*\text{.}$

Figure $2.2.1$: ©Bill Griffith. Reprinted with permission.

Solution

Let $u,v∈H$. To show $u∗v∈H$, we need to show that $(u∗v)∗(u∗v)=u∗v$. Now,

$\begin{array}& (u∗v)∗(u∗v)&=u∗(v∗u)∗v &(\text{since } ∗ \text{ is associative}) \\&=u∗(u∗v)∗v &(\text{since } ∗ \text{ is commutative}) \\&=(u∗u)∗(v∗v) &(\text{since } ∗ \text{ is associative}) \\&=u∗v &(\text{since } u,v∈H) . \end{array}$

So $u∗v∈H$.

Exercise 2.8 (Part II)

1. True/False. For each of the following, write T if the statement is true; otherwise, write F. You do NOT need to provide explanations or show work for this problem.

For every positive integer $n\text{,}$ there exists a group of order $n\text{.}$
For every integer $n\geq 2\text{,}$ $\mathbb{Z}_n$ is abelian.
Every abelian group is finite.
For every integer $m$ and integer $n\geq 2\text{,}$ there exist infinitely many integers $a$ such that $a$ is congruent to $m$ modulo $n\text{.}$
A binary operation $*$ on a set $S$ is commutative if and only if there exist $a,b\in S$ such that $a*b=b*a\text{.}$
If $\langle S, *\rangle$ is a binary structure, then the elements of $S$ must be numbers.
If $e$ is an identity element of a binary structure (not necessarily a group) $\langle S,*\rangle\text{,}$ then $e$ is an idempotent in $S$ (that is, $e*e=e$).
If $s$ is an idempotent in a binary structure (not necessarily a group) $\langle S,*\rangle\text{,}$ then $s$ must be an identity element of $S\text{.}$

Solution

T
T
F
T
F
F
T
F

2. Let $G$ be the set of all functions from $\mathbb{Z}$ to $\mathbb{R}\text{.}$ Prove that pointwise multiplication on $G$ (that is, the operation defined by $(fg)(x)=f(x)g(x)$ for all $f,g\in G$ and $x\in \mathbb{Z}$) is commutative. (Note. To prove that two functions, $h$ and $j\text{,}$ sharing the same domain $D$ are equal, you need to show that $h(x)=j(x)$ for every $x\in D\text{.}$)

Solution

Let $f,g∈G$. Then for every $x∈\mathbb{Z}$,

$(fg)(x)=f(x)g(x)=g(x)f(x)$,

since $f(x),g(x)∈\mathbb{R}$ and multiplication of real numbers is commutative. Since $g(x)f(x)=(gf)(x)$, $fg=gf$, and so pointwise multiplication on $G$ is commutative.

3. Decide which of the following binary structures are groups. For each, if the binary structure isn't a group, prove that. (Remember, you should not state that inverses do or do not exist for elements until you have made sure that the structure contains an identity element!) If the binary structure is a group, prove that.

$\mathbb{Q}$ under multiplication
$\mathbb{M}_2(\mathbb{R})$ under addition
$\mathbb{M}_2(\mathbb{R})$ under multiplication
$\mathbb{R}^+$ under $*\text{,}$ defined by $a*b=\sqrt{ab}$ for all $a,b\in \mathbb{R}^+$

Solution

$\mathbb{Q}$ isn't a group under multiplication since $0∈\mathbb{Q}$ has no inverse.
Matrix multiplication is always associative, and the zero matrix in $\mathbb{M}^2(\mathbb{R})$ acts as an additive identity element. Finally, let $A∈\mathbb{M}^2(\mathbb{R})$. Then $−A∈\mathbb{M}^2(\mathbb{R})$ is an inverse for $A$ under addition. Thus, $\mathbb{M}^2(\mathbb{R})$ is a group under addition.
$\mathbb{M}^2(\mathbb{R})$isn't a group under multiplication since the zero matrix has no inverse.
$1∗(4∗9)=1∗6=\sqrt{6}$ while $(1∗4)∗9=2∗9=\sqrt{18}$, so $∗$ isn't associative. Thus, $\mathbb{R}^+$ isn't a group under $∗$.

4. Give an example of an abelian group containing 711 elements.

Solution

$\mathbb{Z}_{711}$. (Other answers are possible.)

5. Let $n\in \mathbb{Z}\text{.}$ Prove that $n\mathbb{Z}$ is a group under the usual addition of integers. Note: You may use the fact that $\langle n\mathbb{Z},+\rangle$ is a binary structure if you provide a reference for this fact.

Solution

We know from Theorem $2.6.1$ that $\langle n\mathbb{Z},+ \rangle$ is a binary structure.

Next, $+$ is associative on $n$, since it's associative on $\mathbb{Z}$, and $n\mathbb{Z}⊆\mathbb{Z}$.

Notice that $0∈n\mathbb{Z}$ (since $0=n(0)$); $0$ then clearly acts as an identity element for $+$ in $n\mathbb{Z}$.

Finally, let $x∈n\mathbb{Z}$, then $x=nm$ for some $m∈\mathbb{Z}$, so $−x=n(−m)$ for $m∈\mathbb{Z}$, implying $−x∈n\mathbb{Z}$; and clearly $−x$ acts as an inverse for $x$ in $n\mathbb{Z}$.

Thus, $\langle n\mathbb{Z},+ \rangle$ is a group.

6. Let $n\in \mathbb{Z}^+\text{.}$ Prove that $SL(n,\mathbb{R})$ is a group under matrix multiplication. Note: You may use the fact that $\langle SL(n\mathbb{R}),\cdot\rangle$ is a binary structure if you provide a reference for this fact.

Solution

We know from Theorem $2.4.2$ that $\langle SL(n,\mathbb{R}), \cdot \rangle$ is a binary structure,and we know that matrix multiplication is always associative. Next, since $\text{det }I_n=1$, $I_n$ is in $SL(n,\mathbb{R})$, and clearly acts as an identity element in $SL(n,\mathbb{R})$. Finally, let $A∈SL(n,\mathbb{R})$. Since $\text{det }A=1≠0$, $A$ has an inverse matrix $A^{−1}$ in $GL(n,\mathbb{R})$. $A^{−1}$ is in $SL(n,\mathbb{R})$ since

$\text{det }(A^{−1})=\dfrac{1}{\text{det }A}=\dfrac{1}{1}=1.$

So $A$ has an inverse in $SL(n,\mathbb{R})$.

Thus, our proof is complete.

7.

List three distinct integers that are congruent to $6$ modulo $5\text{.}$
List the elements of $\mathbb{Z}_5\text{.}$
Compute:
1. $4+5$ in $\mathbb{Z}\text{;}$
2. $4+5$ in $\mathbb{Q}\text{;}$
3. $4+_65$ in $\mathbb{Z}_6\text{;}$
4. the inverse of $4$ in $\mathbb{Z}\text{;}$
5. the inverse of $4$ in $\mathbb{Z}_6\text{.}$
Why does it not make sense for me to ask you to compute $4+_3 2$ in $\mathbb{Z}_3\text{?}$ Please answer this using a complete, grammatically correct sentence.

Solution

$11,1,−4$. (Other answers are possible.)
$\mathbb{Z}_5=\{0,1,2,3,4\}$
Compute:
1. $9$
2. $9$
3. $3$
4. $-4$
5. $2$
It doesn't make sense because $4∉\mathbb{Z}_3$.

8. Let $G$ be a group with identity element $e\text{.}$ Prove that if every element of $G$ is its own inverse, then $G$ is abelian.

Solution

Let $a,b∈G$. Then

$\begin{array}& ab&=(ab)^{−1} &(\text{since } ab \text{ is its own inverse}) \\&=b^{−1}a^{−1}&=ba, \end{array}$

since $a,b$ are their own inverses.

So $G$ is abelian.

Let $a,b\in G\text{.}$ Then

So $G$ is abelian.

9. Let $G$ be a group. The subset

\begin{equation*} Z(G):=\{z \in G\,:\, zg=gz \mbox{ for all } g\in G\} \end{equation*}

of $G$ is called the center of $G\text{.}$ In other words, $Z(G)$ is the set of all elements of $G$ that commute with every element of $G\text{.}$ Prove that $Z(G)$ is closed in $G\text{.}$

Solution

Let $z_1,z_2∈Z(G)$. Let $z=z_1z_2$; we want to show that $z$ is in $H$: that is, we want to show that for every $g∈G$, $zg=gz$. But for every $g∈G$,

$\begin{array}& zg&=(z_1z_2)g &(\text{using the definition of \(z$}) \\&=z_1(z_2g) &(\text{since $G$'s operation is associative}) \\&=z_1(gz_2) &(\text{since } z_2∈Z(G)) \\&=(z_1g)z_2 &(\text{since $G$'s operation is associative}) \\&=(gz_1)z_2 &(\text{since } z_1∈Z(G)) \\&=g(z_1z_2) &(\text{since $G$'s operation is associative}) \\&=g_z &(\text{using the definition of }h) \end{array}\).

Thus, $Z(G)$ is closed in $G$.

Exercise 3.4

1. True/False. For each of the following, write T if the statement is true; otherwise, write F. You do NOT need to provide explanations or show work for this problem. Throughout, let $G$ and $G'$ be groups.

If there exists a homomorphism $\phi\;:\;G\to G'\text{,}$ then $G$ and $G'$ must be isomorphic groups.
There is an integer $n\geq 2$ such that $\mathbb{Z}\simeq \mathbb{Z}_n\text{.}$
If $|G|=|G'|=3\text{,}$ then we must have $G\simeq G'\text{.}$
If $|G|=|G'|=4\text{,}$ then we must have $G\simeq G'\text{.}$

Solution

F
F
T
F

2. For each of the following functions, prove or disprove that the function is (i) a homomorphism; (ii) an isomorphism. (Remember to work with the default operation on each of these groups!)

The function $f:\mathbb{Z}\to\mathbb{Z}$ defined by $f(n)=2n\text{.}$
The function $g:\mathbb{R}\to\mathbb{R}$ defined by $g(x)=x^2\text{.}$
The function $h:\mathbb{Q}^*\to\mathbb{Q}^*$ defined by $h(x)=x^2\text{.}$

Solution

1. The function $f$ is a homomorphism, since for every $a,b∈\mathbb{Z}$, we have
  $f(a+b)=2(a+b)=2a+2b=f(a)+f(b)$.
2. The function $f$ isn't a bijection, since it isn't onto: for instance, there is no element aa in $\mathbb{Z}$ such that $f(a)=3$. Thus, $f$ is not an isomorphism.
1. The function $g$ isn't a homomorphism: for instance, we have
  $g(2+3)=g(5)=25≠13=4+9=g(2)+g(3)$.
2. Since it isn't a homomorphism, it isn't an isomorphism.
1. The function $h$ is a homomorphism, since for every $a,b∈\mathbb{Q}$, we have
  $h(ab)=(ab)^2=a^2b^2=h(a)h(b)$.
2. The function $h$ isn't onto: its range is the set of nonnegative rational numbers, not all of $\mathbb{Q}$. Thus, $h$ is not an isomorphism.

3. Define $d : GL(2,\mathbb{R})\to \mathbb{R}^*$ by $d(A)=\text{det } A\text{.}$ Prove/disprove that $d$ is:

a homomorphism
1-1
onto
an isomorphism.

Solution

The function $d$ is a homomorphism, since for every $A,B∈GL(2,\mathbb{R})$, we have
$d(AB)=\text{det }(AB)=(\text{det }A)(\text{det }B)=d(A)d(B)$.
$d$ isn't 1-1: For instance, $d(I_2)=d(−I_2)$.
$d$ is onto: Let $a∈\mathbb{R}^∗$. Then the matrix
$A=\begin{bmatrix} a & 0\\0 & 1\end{bmatrix}$
is in $GL(2,\mathbb{R})$, with $d(A)=a$.
Since $d$ isn't 1-1, it isn't an isomorphism.

4. Complete the group tables for $\mathbb{Z}_4$ and $\mathbb{Z}_8^{\times}\text{.}$ Use the group tables to decide whether or not $\mathbb{Z}_4$ and $\mathbb{Z}_8^{\times}$ are isomorphic to one another. (You do not need to provide a proof.)

Solution

The group tables of $\mathbb{Z}_4$ and $\mathbb{Z}^×_8$ are, respectively,

$+$	$0$	$1$	$2$	$3$
$0$	$0$	$1$	$2$	$3$
$1$	$1$	$2$	$3$	$0$
$2$	$2$	$3$	$0$	$1$
$3$	$3$	$0$	$1$	$2$

and

$\cdot s$	$1$	$3$	$5$	$7$
$1$	$1$	$3$	$5$	$7$
$3$	$3$	$5$	$7$	$1$
$5$	$5$	$7$	$1$	$3$
$7$	$7$	$1$	$3$	$5$

We can see from the group table for $\mathbb{Z}^×_8$ that every element of that group is its own inverse; that is not the case in $\mathbb{Z}_4$. Thus, $\mathbb{Z}_4≄\mathbb{Z}^×_8$.

5. Let $n\in \mathbb{Z}^+\text{.}$ Prove that $\langle n\mathbb{Z},+\rangle \simeq \langle \mathbb{Z},+\rangle\text{.}$

Solution

Define $ϕ:\mathbb{Z}→n\mathbb{Z}$ by $ϕ(x)=nx$, for all $x∈\mathbb{Z}$. Clearly, $ϕ$ is a bijection. Moreover, for all $x,y∈\mathbb{Z}$,

$ϕ(x+y)=n(x+y)=nx+ny=ϕ(x)+ϕ(y)$;

so $ϕ$ is a homomorphism. Thus, $ϕ$ is an isomorphism, and hence

$\langle \mathbb{Z},+ \rangle ≃ \langle n\mathbb{Z},+ \rangle$.

6.

Let $G$ and $G'$ be groups, where $G$ is abelian and $G\simeq G'\text{.}$ Prove that $G'$ is abelian.
Give an example of groups $G$ and $G'\text{,}$ where $G$ is abelian and there exists a homomorphism from $G$ to $G'\text{,}$ but $G'$ is NOT abelian.

Solution

Since $G≃G′$, there exists some isomorphism $ϕ:G→G′$. Let $x,y∈G′$. Since $ϕ$ is onto, there exist $a,b∈G$ such that $ϕ(a)=x$ and $ϕ(b)=y$. So
$\begin{array}& xy&=ϕ(a)ϕ(b)\\ &=ϕ(ab) &(\text{since } ϕ \text{ is a homomorphism}) \\&=ϕ(ba) &(\text{since } G \text{ is abelian}) \\&=ϕ(b)ϕ(a)\\&=yx. \end{array}$
Thus, $G′$ is abelian.
Let $G=\{I_2\}$ (under multiplication) and let $G′=GL(2,\mathbb{R})$. Then the map $ϕ:G→G′$ defined by $ϕ(I_2)=I_2$ is clearly a homomorphism, but note that $G$ is abelian while $G′$ is not.

7. Let $\langle G,\cdot\rangle$ and $\langle G',\cdot'\rangle$ be groups with identity elements $e$ and $e'\text{,}$ respectively, and let $\phi$ be a homomorphism from $G$ to $G'\text{.}$ Let $a\in G\text{.}$ Prove that $\phi(a)^{-1}=\phi(a^{-1})\text{.}$

Solution

We omit the group operations in this solution in order to increase familiarity with the convention.

We want to show that $ϕ(a)^{−1}=ϕ(a^{−1})$. Notice that

$\begin{array} &ϕ(a^{−1})ϕ(a) & =ϕ(a^{−1}a) & (\text{since \(ϕ$ is a homomorphism}) \\ & =ϕ(e) & (\text{by definition of } a^{−1})\\ &=e′ & (\text{since $ϕ(e)$ is the identity element of } G′) \\& =ϕ(a)^{−1}ϕ(a) & (\text{by definition of } ϕ(a)^{−1}). \end{array}\)

Thus, $ϕ(a^{−1})=ϕ(a)^{−1}$, by right cancellation.

Exercise 4.3

1. True/False. For each of the following, write T if the statement is true; otherwise, write F. You do NOT need to provide explanations or show work for this problem. Throughout, let $G$ and $G'$ be groups.

Every group contains at least two distinct subgroups.
If $H$ is a proper subgroup of group $G$ and $G$ is finite, then we must have $|H|\lt |G|\text{.}$
$7\mathbb{Z}$ is a subgroup of $14\mathbb{Z}\text{.}$
A group $G$ may have two distinct proper subgroups which are isomorphic (to one another).

Solution

F
T
F
T

2. Give specific, precise examples of the following groups $G$ with subgroups $H\text{:}$

A group $G$ with a proper subgroup $H$ of $G$ such that $|H|=|G|\text{.}$
A group $G$ of order 12 containing a subgroup $H$ with $|H|=3\text{.}$
A nonabelian group $G$ containing a nontrivial abelian subgroup $H\text{.}$
A finite subgroup $H$ of an infinite group $G\text{.}$

Solution

(Other answers are possible.)

$G=\mathbb{Z}$, $H=2\mathbb{Z}$
$G=\mathbb{Z}_{12}$, $H=\{0,4,8\}$
$G=GL(2,\mathbb{R})$, $H=\{±I_2\}$
$G=\mathbb{R}^∗$, $H=\{±1\}$.

3. Let $n\in \mathbb{Z}^+\text{.}$

Prove that $n\mathbb{Z} \leq \mathbb{Z}\text{.}$
Prove that the set $H=\{A\in \mathbb{M}_n(\mathbb{R})\,:\,\det A=\pm 1\}$ is a subgroup of $GL(n,\mathbb{R})\text{.}$

(Note: Your proofs do not need to be long to be correct!)

Solution

We know that $n\mathbb{Z}⊆\mathbb{Z}$ and that $n\mathbb{Z}$ is a group under addition, the group operation in $\mathbb{Z}$. Therefore, $n\mathbb{Z}≤\mathbb{Z}$.
Clearly, $H$ is a nonempty subset of $GL(n,\mathbb{R})$ (for instance, $I_n∈H$). Next, let $A,B∈H$. Then
$\text{det }(AB^{−1})=(\text{det }A)(\text{det }(B^{−1}))=(±1)(1±1)=±1$,
so $AB^{−1}∈H$. Thus, $H≤GL(n,\mathbb{R})$ by the Two-Step Subgroup Test.

4. Let $n\in \mathbb{Z}^+\text{.}$ For each group $G$ and subset $H\text{,}$ decide whether or not $H$ is a subgroup of $G\text{.}$ In the cases in which $H$ is not a subgroup of $G\text{,}$ provide a proof. (Note. Your proofs do not need to be long to be correct!)

$G=\mathbb{R}\text{,}$ $H=\mathbb{Z}$
$G=\mathbb{Z}_{15}\text{,}$ $H=\{0,5,10\}$
$G=\mathbb{Z}_{15}\text{,}$ $H=\{0,4,8,12\}$
$G=\mathbb{C}\text{,}$ $H=\mathbb{R}^*$
$G=\mathbb{C}^*\text{,}$ $H=\{1,i,-1,-i\}$
$G=\mathbb{M}_n(\mathbb{R})\text{,}$ $H=GL(n,\mathbb{R})$
$G=GL(n,\mathbb{R})\text{,}$ $H=\{A\in \mathbb{M}_n(\mathbb{R})\,:\,\det A = -1\}$

Solution

$H≤G$.
$H≤G$.
$H$ is a subset of $G$ but isn't closed under $+_{15}$: for instance $12+_{15}4=1∉H$. So $H \nleq G$.
$H$ is a subset of $G$, but the identity element, $0$, of $G$ isn't in $H$, so $H \nleq G$.
$H≤G$.
$H$ is a subset of $G$, but the identity element, $0$, of $G$ isn't in $H$, so $H \nleq G$.
$H$ is a subset of $G$, but the identity element, $I_n$, of $G$ isn't in $H$, since $\text{det }I_n=1$. Thus, $H \nleq G$.

5. Let $G$ and $G'$ be groups, let $\phi$ be a homomorphism from $G$ to $G'\text{,}$ and let $H$ be a subgroup of $G\text{.}$ Prove that $\phi(H)$ is a subgroup of $G'\text{.}$

Solution

Let $x,y∈ϕ(H)$. Then $x=ϕ(a)$ and $y=ϕ(b)$ for some $a,b∈H$. So $xy=ϕ(a)ϕ(b)=ϕ(ab)$ (since $ϕ$ is a homomorphism). Since $H≤G$, $ab∈H$. Thus, $xy∈ϕ(H)$. Next, $e_G∈H$, so $e_G′=ϕ(e_G)∈ϕ(H)$. Finally, since $H≤G$ and $a∈H$, $a^{−1}∈H$; so $x^{−1}=ϕ(a)^{−1}=ϕ(a^{−1})∈ϕ(H)$. Thus, $ϕ(H)≤G′$.

6. Let $G$ be an abelian group, and let $U=\{g\in G\,:\, g^{-1}=g\}.$ Prove that $U$ is a subgroup of $G\text{.}$

Solution

Clearly, $U⊆G$ and $e∈U$. Next, let $u,v∈U$. Then

$(uv)^2=(uv)(uv)=u^2v^2=uv$,

so $uv∈U$. Finally, since $u∈U$, we have $u^{−1}=u$, so $(u^{−1})^2=u^2=e$; thus, $u^{−1}∈U$.

Exercise 5.3

1. True/False. For each of the following, write T if the statement is true; otherwise, write F. You do NOT need to provide explanations or show work for this problem. Throughout, let $G$ be a group with identity element $e\text{.}$

If $G$ is infinite and cyclic, then $G$ must have infinitely many generators.
There may be two distinct elements $a$ and $b$ of a group $G$ with $\langle a\rangle =\langle b\rangle\text{.}$
If $a,b\in G$ and $a\in \langle b\rangle$ then we must have $b\in \langle a\rangle\text{.}$
If $a\in G$ with $a^4=e\text{,}$ then $o(a)$ must equal $4\text{.}$
If $G$ is countable then $G$ must be cyclic.

Solution

F
T
F
F
F

2. Give examples of the following.

An infinite noncyclic group $G$ containing an infinite cyclic subgroup $H\text{.}$
An infinite noncyclic group $G$ containing a finite nontrivial cyclic subgroup $H\text{.}$
A cyclic group $G$ containing exactly 20 elements.
A nontrivial cyclic group $G$ whose elements are all matrices.
A noncyclic group $G$ such that every proper subgroup of $G$ is cyclic.

Solution

(Other answers are possible.)

$G=\mathbb{R}$, $H=\mathbb{Z}$
$G=GL(n,\mathbb{R})$, $H=\{±I_2\}$
$G=\mathbb{Z}_{20}$
$G=\{±I_2\}$, under matrix multiplication
$G=\mathbb{Z}_2^2$

3. Find the orders of the following elements in the given groups.

$2\in \mathbb{Z}$
$-i\in \mathbb{C}^*$
$-I_2\in GL(2,\mathbb{R})$
$-I_2\in \mathbb{M}_2(\mathbb{R})$
$(6,8)\in \mathbb{Z}_{10}\times \mathbb{Z}_{10}$

Solution

$o(2)=∞$, since $ \langle 2 \rangle =2\mathbb{Z}$.
$o(−i)=4$, since $\langle −i \rangle =\{−i,−1,i,1\}$.
$o(I_2)=2$, since $\langle−I_2 \rangle=\{−I_2,I_2\}$.
$o(I_2)=∞$, since $\langle −I_2 \rangle =\{kI_2:k∈\mathbb{Z}\}$.
$o((6,8))=5$, since $\langle (6,8) \rangle=\{(6,8),(2,6),(8,4),(4,2),(0,0)\}$.

4. For each of the following, if the group is cyclic, list all of its generators. If the group is not cyclic, write NC.

$5\mathbb{Z}$
$\mathbb{Z}_{18}$
$\mathbb{R}$
$\langle \pi\rangle$ in $\mathbb{R}$
$\mathbb{Z}_2^2$
$\langle 8\rangle$ in $\mathbb{Q}^*$

Solution

$±5$
$1,5,7,11,13,17$
NC
$±π$
NC
$8,\dfrac{1}{8}$

5. Explicitly identify the elements of the following subgroups of the given groups. You may use set-builder notation if the subgroup is infinite, or a conventional name for the subgroup if we have one.

$\langle 3\rangle$ in $\mathbb{Z}$
$\langle i\rangle$ in $C^*$
$\langle A\rangle\text{,}$ for $A=\left[ \begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array} \right]\in \mathbb{M}_2(\mathbb{R})$
$\langle (2,3)\rangle$ in $\mathbb{Z}_4\times \mathbb{Z}_5$
$\langle B\rangle\text{,}$ for $B=\left[ \begin{array}{cc} 1 & 1\\ 0 & 1 \end{array} \right]\in GL(2,\mathbb{R})$

Solution

$3\mathbb{Z}$
$\{i,−1,−i,1\}$
$\{\left[ \begin{array}{cc} k & 0 \\ 0 & 0 \end{array} \right]:k∈\mathbb{Z}\}$
$\{(2,3),(0,1),(2,4),(0,2),(2,0),(0,3),(2,1),(0,4),(2,2),(0,0)\}$
$\{\left[ \begin{array}{cc} 1 & k \\ 0 & 1 \end{array} \right]:k∈\mathbb{Z}\}$

6. Draw subgroup lattices for the following groups.

$\mathbb{Z}_6$
$\mathbb{Z}_{13}$
$\mathbb{Z}_{18}$

The respective solutions are:

Solution

The respective solutions are:

a.

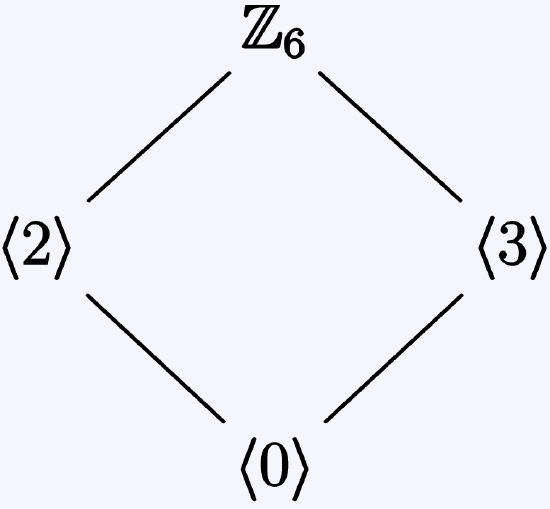
$clipboard_ec4d4f68fbd356817a531707567fdb823.png$

b.

$clipboard_eec713a0eaf19850992c7106830fd9b3c.png$

c.

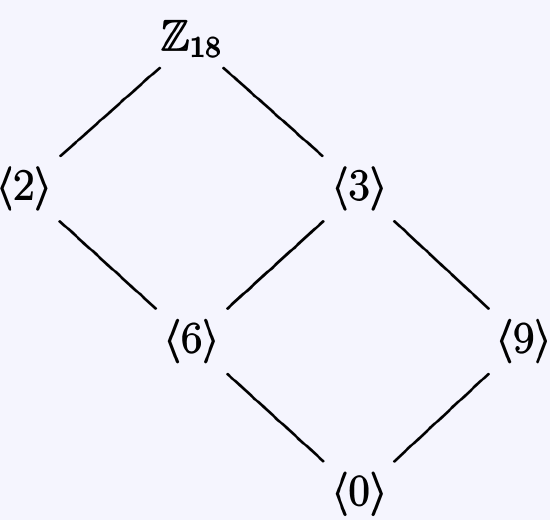
$clipboard_efe02f0f83f1510eb887a3dd3b1053619.png$

7. Let $G$ be a group with no nontrivial proper subgroups. Prove that $G$ is cyclic.

Solution

Let $e$ be the identity element of $G$. If $G=\{e\}$, then $G$ is clearly cyclic. Else, there exists $a≠e$ in $G$. Then $\langle a \rangle$ is a subgroup of $G$. Since $e≠a∈ \langle a \rangle$, $\langle a \rangle$ is a nontrivial subgroup of $G$. Therefore, we must have $\langle a \rangle =G$. Hence, $G$ is cyclic, as desired.

Exercise 6.6

1. Let $\sigma=(134)\text{,}$ $\tau=(23)(145)\text{,}$ $\rho=(56)(78)\text{,}$ and $\alpha=(12)(145)$ in $S_8\text{.}$ Compute the following.

$\sigma \tau$
$\tau \sigma$
$\tau^2$
$\tau^{-1}$
$o(\tau)$
$o(\rho)$
$o(\alpha)$
$\langle \tau\rangle$

Solution

$στ=(134)(23)(145)=(2453)$
$τσ=(23)(145)(134)=(1235)$
$τ^2=(154)$
$τ−1=(23)(154)$
$o(τ)= \text{lcm}⁡(2,3)=6 (\text{since } (23) \text{ and } (145) \text{ are disjoint})$
$o(ρ)= \text{lcm}⁡(2,2)=2$
In disjoint cycle notation, $α=(1452)$, so $o(α)=o(1452)=4$.
$\langle τ \rangle ={(23)(145),(154),(23),(145),e}$

2. Prove Lemma 6.3.1.

Solution

Let $σ=(a_1a_2⋯a_k)∈S_n$. Then $σ=(a_1a_k)(a_1a_{k_{−1}})⋯(a_1a_3)(a_1a_2)$, so is a product of $k−1$ transpositions. Thus, $σ$ is even if $k−1$ is even, that is, if $k$ is odd, and odd if $k−1$ is odd, that is, if $k$ is even.

3. Prove that $A_n$ is a subgroup of $S_n\text{.}$

Solution

Since $e∈A_n$, $A_n≠∅$. Next, let $σ,τ∈A_n$. Then $σ$ can be written as a product of $k$ transpositions and $τ$ can be written as $τ=τ_1τ_2⋯τ_m$, where $k$ and mm are even and the $τ_i$ are transpositions. Since each $τ_i$ is a transposition, each $τ_i$ is its own inverse; so

$τ^{−1}=(τ_m)^{−1}(τ_{m−1})^{−1}⋯τ^{−1}_1=τ_m^{−1}τ_{m-1}^{−1}⋯τ_1^{−1}$.

Thus, $στ^{−1}$ is a product of $k+m$ transpositions; since $k$ and $m$ are even, $k+m$ is even, and so $στ^{−1}∈A_n$. Thus, $A_n≤S_n$, by the Two-Step Subgroup Test.

4. Prove or disprove: The set of all odd permutations in $S_n$ is a subgroup of $S_n\text{.}$

Solution

This set is not a subgroup of $S_n$ because, for instance, it doesn't contain $e$.

5. Let $n$ be an integer greater than $2$. $m \in \{1,2,\ldots,n\}\text{,}$ and let $H=\{\sigma\in S_n\,:\,\sigma(m)=m\}$ (in other words, $H$ is the set of all permutations in $S_n$ that fix $m$).

Prove that $H\leq S_n\text{.}$
Identify a familiar group to which $H$ is isomorphic. (You do not need to show any work.)

Solution

Since $e∈H$, $H≠∅$. Next, let $σ,τ∈H$. Since $τ(m)=m$ and $τ$ is a bijection, $τ^{−1}(m)=m$. So $στ^{−1}(m)=σ(τ^{−1}(m))=σ(m)=m$. So $στ^{−1}∈H$; therefore, $H≤S_n$, by the Two-Step Subgroup Test.
$S_{n−1}$.

6. Write $rfr^2frfr$ in $D_5$ in standard form.

Solution

In $D_5$, $frfr=(fr)^2=e$ and $rf=fr^{−1}$, so

$rfr^2frfr=rfr^2=fr^{−1}r^2=fr.$

7. Prove or disprove: $D_6\simeq S_6\text{.}$

Solution

$|D_6|=2(6)=12$ while $|S_6|=720$, so $D_6≄S_6$.

8. Which elements of $D_4$ (if any)

have order $2$?
have order $3\text{?}$

Solution

We know $o(fr^i)=2$ for every $i$, and $o(e)=1$. Moreover, since $4$ is even, $r^{4/2}=r^2$ has order $2$. Finally, $o(r)=o(r^{−1})=4$. So (a) the elements of order $2$ in $D_4$ are $f, fr,fr^2, fr^3$, and $r^2$, and (b) $D_4$ contains no elements of order $3$.

9. Let $n$ be an even integer that's greater than or equal to $4$. Prove that $r^{n/2}\in Z(D_n)\text{:}$ that is, prove that $r^{n/2}$ commutes with every element of $D_n\text{.}$ (Do NOT simply refer to the last statement in Theorem 6.5.4; that is the statement you are proving here.)

Solution

Clearly, $r^{n/2}$ commutes with every $r^k$ for $0≤k≤n$. Moreover, by the first statement of Theorem 6.5.4,

$r^{n/2}f=f(r^{n/2})^{−1}=fr^{n−n/2}=fr^{n/2}$.

So $r^{n/2}$ commutes with $f$. It clearly follows that $r^{n/2}∈\mathbb{Z}(D_n)$.

Exercise 7.4

1. How many distinct partitions of the set $S=\{a,b,c,d\}$ are there? You do not need to list them. (Yes, you can find this answer online. But I recommend doing the work yourself for practice working with partitions!)

Solution

There are 15 distinct partitions of the set $\{a,b,c,d\}$:

$\{\{a\},\{b\},\{c\},\{d\}\},\{\{a,b\},\{c\},\{d\}\},\{\{a,c\},\{b\},\{d\}\},\{\{a,d\},\{b\},\{c\}\}, \\ \{\{b,c\},\{a\},\{d\}\},\{\{b,d\},\{a\},\{c\}\},\{\{c,d\},\{a\},\{b\}\}, \\ \{\{a,b\},\{c,d\}\},\{\{a,c\},\{b,d\}\},\{\{a,d\},\{b,c\}\}, \\ \{\{a,b,c\},\{d\}\},\{\{a,b,d\},\{c\}\},\{\{a,c,d\},\{b\}\},\{\{b,c,d\},\{a\},\}, \\ \{\{a,b,c,d\}\}.$

2.

Let $n\in \mathbb{Z}^+\text{.}$ Prove that $\equiv_n$ is an equivalence relation on $\mathbb{Z}\text{.}$
The cells of the induced partition of $\mathbb{Z}$ are called the residue classes (or congruence classes) of $\mathbb{Z}$ modulo $n$. Using set notation of the form $\{\ldots,\#, \#,\#,\ldots\}$ for each class, write down the residue classes of $\mathbb{Z}$ modulo $4\text{.}$

Solution

First, for every $x∈\mathbb{Z}$, $n$ divides $0=x−x$; so $x≡_nx$ for every $x∈\mathbb{Z}$. Thus, $≡_n$ is reflexive. Next, let $x,y∈\mathbb{Z}$ with $x≡_ny$. Then there exists some $q∈\mathbb{Z}$ with $x−y=nq$; so $y−x=n(−q)$. Since $−q∈\mathbb{Z}$, this shows us that $y≡_nx$. Hence, $≡_n$ is symmetric. Finally, let $x,y$ and $z$ be in $\mathbb{Z}$ with $x≡_ny$ and $y≡_nz$. Then there exist $q_1,q_2∈\mathbb{Z}$ with $x−y=nq_1$ and $y−z=nq_2$. Thus,
$x−z=(x−y)+(y−z)=nq_1+nq_2=n(q_1+q_2)$;
since $q_1+q_2∈\mathbb{Z}$, this shows us that $x≡_nz$. Thus, $≡_n$ is transitive. Hence, $≡_n$ is an equivalence relation, as desired.
$\{…,−8,−4,0,4,…\},\{…,−7,−3,1,5,…\},\\ \{…,−6,−2,2,6,…\},\{…,−5,−1,3,7,…\}$

3. Let $G$ be a group with subgroup $H\text{.}$ Prove that $\sim_R$ is an equivalence relation on $G\text{.}$

Solution

First, let $a∈G$. Then $aa^{−1}=e∈H$, so $a\sim_Ra$. Thus, $\sim_R$ is reflexive.

Next, let $a,b∈G$ with $a sim_Rb$. Then $ab^{−1}∈H$, so, since $H$ is a subgroup of $G$, $(ab^{−1})^{−1}∈H$. But $(ab^{−1})^{−1}=ba^{−1}$; thus, $b \sim_Ra$, and so $\sim_R$ is symmetric.

Finally, let $a,b,c∈G$ with $a \sim_Rb$ and $b \sim_Lc$. Then $ab^{−1}$ and $bc^{−1}$ are in $H$. Since $H$ is a subgroup of $G$, we must then have $(ab^{−1})(bc^{−1})∈H$; but $(ab^{−1})(bc^{−1})$ equals $ac^{−1}$. Thus, $a\sim_Rc$, and so $\sim_R$ is transitive.

Hence, $\sim_R$ is an equivalence relation on $G$, as desired.

4. Find the indices of:

$H=\langle (15)(24)\rangle$ in $S_5$
$K=\langle (2354)(34)\rangle$ in $S_6$
$A_n$ in $S_n$

Solution

$(S_5:H)=\dfrac{|S_5|}{|H|}= \dfrac{120}{2} =60$.
In disjoint cycle notation, the permutation $(2354)(34)$ is written $(23)(45)$, so $L$ has order $2$. Thus, $(S_6:K)=\dfrac{|S_6|}{|K|}=\dfrac{720}{2}=360$.
$(S_n:A_n)=2$.

5. For each subgroup $H$ of group $G\text{,}$ (i) find the left and the right cosets of $H$ in $G\text{,}$ (ii) decide whether or not $H$ is normal in $G\text{,}$ and (iii) find $(G:H)\text{.}$

Write all permutations using disjoint cycle notation, and write all dihedral group elements using standard form.

$H=6\mathbb{Z}$ in $G=2\mathbb{Z}$
$H=\langle 4\rangle$ in $\mathbb{Z}_{20}$
$H=\langle (23)\rangle$ in $G=S_3$
$H=\langle r\rangle$ in $G=D_4$
$H=\langle f\rangle$ in $G=D_4$

Solution

1. The left and the right cosets of $6\mathbb{Z}$ in $2\mathbb{Z}$ are $6\mathbb{Z}$, $2+6\mathbb{Z}=6\mathbb{Z}+2$, and $4+6\mathbb{Z}=6\mathbb{Z}+4$.
2. $6\mathbb{Z}⊴2\mathbb{Z}$.
3. $(2\mathbb{Z}:6\mathbb{Z})=3$.
1. The left and the right cosets of $H= \langle 4 \rangle=\{0,4,8,12,16\}$ in $\mathbb{Z}_{20}$ are $H$, $1+H=\{1,5,9,13,17\}=H+1$, $2+H=\{2,7,10,14,18\}=H+2$, and $3+H=\{3,8,11,15,19\}=H+3$.
2. $H⊴Z_{20}$.
3. $(Z_{20}:H)=4$.
1. The left cosets of $H$ in $S_3$ are $H=\{e,(23)\}$, $(12)H=\{(12),(123)\}$, and $(13)H=\{(13),(132)\}$. The right cosets of $H$ in $S_3$ are $H$, $H(12)=\{(12),(132)\}$, and $H(13)=\{(13),(123)\}$.
2. $H$ is not normal in $S_3$.
3. $(S_3:H)=3$.
1. The left cosets and the right cosets of $H$ in $D_4$ are $H=\{e,r,r^2,r^3\}$ and $fH=\{f,fr,fr^2,fr^3\}=Hf$.
2. $H⊴D_4$.
3. $(D_4:H)=2$.
1. The left cosets of $H$ in $D_4$ are $H=\{e,f\}$, $rH=\{r,fr^3\}$, $r^2H=\{r^2,fr^2\}$, and $r^3H=\{r^3,fr\}$. The right cosets of $H$ in $D_4$ are $H$, $Hr=\{r,fr\}$, $Hr^2=\{r^2,fr^2\}$, and $Hr^3=\{r^3,fr^3\}$.
2. $H$ is not normal in $D_4$.
3. $(D_4:H)=4$.

6. For each of the following, give an example of a group $G$ with a subgroup $H$ that matches the given conditions. If no such example exists, prove that.

A group $G$ with subgroup $H$ such that $|G/H|=1\text{.}$
A finite group $G$ with subgroup $H$ such that $|G/H|=|G|\text{.}$
An abelian group $G$ of order $8$ containing a non-normal subgroup $H$ of order 2.
A group $G$ of order 8 containing a normal subgroup of order $2\text{.}$
A nonabelian group $G$ of order 8 containing a normal subgroup of index $2\text{.}$
A group $G$ of order 8 containing a subgroup of order $3\text{.}$
An infinite group $G$ containing a subgroup $H$ of finite index.
An infinite group $G$ containing a finite nontrivial subgroup $H\text{.}$

Solution

(Other answers are possible.)

$G=H=S_3$.
$G=S_3$, $H=\{e\}$.
No such example exists, since every subgroup of an abelian group is normal.
$G=\mathbb{Z}_8$, $H=\{0,4\}$.
$G=D_4$, $H= \langle r \rangle$.
No such example exists, since by Lagrange's Theorem $|H|$ must divide $|G|$, and $3$ doesn't divide $8$.
$G=\mathbb{Z}$, $H=2\mathbb{Z}$.
$G=GL(2,\mathbb{R})$, $H=\{±I_2\}$.

7. True/False. For each of the following, write T if the statement is true; otherwise, write F. You do NOT need to provide explanations or show work for this problem. Throughout, let $G$ be a group with subgroup $H$ and elements $a,b\in G\text{.}$

If $a\in bH$ then $aH$ must equal $bH\text{.}$
$aH$ must equal $Ha\text{.}$
If $aH=bH$ then $Ha$ must equal $Hb\text{.}$
If $a\in H$ then $aH$ must equal $Ha\text{.}$
$H$ must be normal in $G$ if there exists $a\in G$ such that $aH=Ha\text{.}$
If $aH=bH$ then $ah=bh$ for every $h\in H\text{.}$
$|G/H|$ must be less than $|G|\text{.}$
$(G:H)$ must be less than or equal to $|G|\text{.}$

Solution

T
F
F
T
F
F
F
T

8. Let $G$ be a group of order $pq\text{,}$ where $p$ and $q$ are prime, and let $H$ be a proper subgroup of $G\text{.}$ Prove that $H$ is cyclic.

Solution

By Lagrange's Theorem, $|H|$ divides $pq$, and since $H$ is proper, $|H|≠pq$.Thus, $|H|=1,p$, or $q$. Since the order of $H$ is either $1$ or a prime number, $H$ must be cyclic.

9. Prove Corollary 7.3.2: that is, let $G$ be a group of prime order, and prove that $G$ is cyclic.

Solution

Since $|G|$ is prime, $|G|>1$, so there exists $a∈G$ with $a≠e$. Then $\langle a \rangle$ is a subgroup of $G$, so by Lagrange's Theorem, $|\langle a \rangle|$ divides $|G|$. But $|G|$ is prime and $a≠e$, so we must have $|\langle a \rangle|=|G|$; thus, $G=\langle a \rangle$.

10. Let $G$ be a group of finite order $n\text{,}$ containing identity element $e\text{.}$ Let $a\in G\text{.}$ Prove that $a^n=e\text{.}$

Solution

By Lagrange's Theorem, $o(a)=|\langle a \rangle|$ divides $n$ ; that is, $n=o(a)m$ for some $m∈\mathbb{Z}^+$. Thus,

$a^n=a^{o(a)m}=(a^{o(a)})^m=e^m=e$.

Exercise 8.4

1. Let $G$ be a group and let $H\leq G$ have index 2. Prove that $H\unlhd G\text{.}$

Solution

Let $a∈G$. If $a∈H$, then $aH=H=Ha$. On the other hand, if $a∉H$, then $aH=G−H=Ha$, since $(G:H)=2$. Thus, $H⊴G$.

2. Let $G$ be an abelian group with $N\unlhd G\text{.}$ Prove that $G/N$ is abelian.

Solution

Let $aN,bN∈G/N$. Then

$(aN)(bN)=abN=baN=(bN)(aN)$.

So $G/N$ is abelian.

Let $aN,bN\in G/N.$ Then

So $G/N$ is abelian.

3. Find the following.

$|2\mathbb{Z}/6\mathbb{Z}|$
$|H|\text{,}$ for $H=2+\langle 6\rangle \subseteq \mathbb{Z}_{12}$
$o(2+\langle 6\rangle)$ in $\mathbb{Z}_{12}/\langle 6\rangle$
$\langle f+H\rangle $ in $D_4/H\text{,}$ where $H=\{e,r^2\}$
$|(\mathbb{Z}_6\times \mathbb{Z}_8)/(\langle 3\rangle\times \langle 2\rangle)|$
$|(\mathbb{Z}_{15} \times \mathbb{Z}_{24})/\langle (5,4)\rangle|$

Solution

$|2\mathbb{Z}/6\mathbb{Z}|=(2\mathbb{Z}:6\mathbb{Z})=3$
$\langle 6 \rangle =\{6,0\}$, so $|H|=|\{8,2\}|=2$
$o(2+ \langle 6 \rangle)=3$
$\langle f+H \rangle =\{f+H,H\}$
$|\mathbb{Z}_6×\mathbb{Z}_8|=6(8)=48$ and $|\langle 3 \rangle ×\langle 2 \rangle |=2(4)=8$, so $|\mathbb{Z}_6×\mathbb{Z}_8/\langle 3 \rangle ×\langle 2 \rangle |= \dfrac{48}{8}=6$.
$ \langle(5,4) \rangle=\{(5,4),(10,8),(0,12),(5,16),(10,20),(0,0)\}$; so the order of $(\mathbb{Z}_{15}×\mathbb{Z}_{24})/\langle (5,4) \rangle$ is $\dfrac{(15)(24)}{6}=60$.

4. For each of the following, find a familiar group to which the given group is isomorphic. (Hint: Consider the group order, properties such as abelianness and cyclicity, group tables, orders of elements, etc.)

$\mathbb{Z}/14\mathbb{Z}$
$3\mathbb{Z}/12\mathbb{Z}$
$S_8/A_8$
$(4\mathbb{Z} \times 15\mathbb{Z})/(\langle 2 \rangle \times \langle 3 \rangle )$
$D_4/\langle r^2 \rangle$

Solution

$\mathbb{Z}_{14}$
$3\mathbb{Z}/12\mathbb{Z}$ is cyclic (since $3\mathbb{Z}$ is cyclic) with order $4$, so is isomorphic to $\mathbb{Z}_4$
$S_8/A_8$ has order $2$, so is isomorphic to $\mathbb{Z}_2$.
Since $\text{gcd}(4,15)=1$, the group $4\mathbb{Z}×15\mathbb{Z}$ is cyclic. So since $|4\mathbb{Z}×15\mathbb{Z}|/|\langle 2 \rangle ×\langle 3 \rangle|= \dfrac{60}{10}=6$, we have $(4\mathbb{Z}×15\mathbb{Z})/(\langle 2 \rangle × \langle 3 \rangle)≃\mathbb{Z}_6$.
$|D_4/ \langle r^2 \rangle|= \dfrac{8}{2}=4$, and $f \langle r^2 \rangle$ and $r \langle r^2 \rangle$ in $D_4/ \langle r^2 \rangle$ each have order $2$, so $D_4/ \langle r^2 \rangle≃ \mathbb{Z}_2^2$.

5. Let $H\unlhd G$ with index $k\text{,}$ and let $a\in G\text{.}$ Prove that $a^k\in H\text{.}$

Solution

Since $k=(G:H)$, $|G/H|=k$. Then $aH∈G/H$ has an order, call it $d$, which must divide $|G/H|=k$. So $k=dm$ for some $m∈\mathbb{Z}$. Then $(aH)^k=(aH)^{dm}=((aH)^d)^m=H^m=H$. Since $(aH)^k=a^kH$, we thus have $a^kH=H$, implying that $a^k∈H$, as desired.

Exercise 9.3

1. Let $F$ be the group of all functions from $[0,1]$ to $\mathbb{R}\text{,}$ under pointwise addition. Let

\begin{equation*} N=\{f\in F: f(1/4)=0\}. \end{equation*}

Prove that $F/N$ is a group that's isomorphic to $\mathbb{R}\text{.}$

Solution

Define $Φ:F→\mathbb{R}$ by $Φ(f)=f(14)$, for every $f∈F$. We have that $Φ$ is a homomorphism, since for every $f,g∈F$,

$Φ(f+g)=(f+g) \left(\dfrac{1}{4} \right)=f\left(\dfrac{1}{4} \right)+g\left(\dfrac{1}{4} \right)=Φ(f)+Φ(g)$.

We also have that $Φ$ is onto, since if $r∈\mathbb{R}$, then the constant function $c_r$ defined by

$c_r(x)=r$ for every $x∈[0,1]$

is sent to $r$ by $Φ$. So $Φ(F)=\mathbb{R}$. Finally, if $f∈F$, then

$f∈\text{Ker}Φ⇔Φ(f)=0⇔f \left(\dfrac{1}{4} \right)=0⇔f∈N$;

so $\text{Ker}⁡Φ=N$. Thus, $F/N≅\mathbb{R}$, by the First Isomorphism Theorem.

2. Let $N=\{1,-1\}\subseteq \mathbb{R}^*\text{.}$ Prove that $\mathbb{R}^*/N$ is a group that's isomorphic to $\mathbb{R}^+\text{.}$

Solution

Define $Φ:\mathbb{R}^∗→\mathbb{R}^+$ by $Φ(x)=|x|$. We know that $Φ$ is a homomorphism, since $Φ(xy)=|xy|=|x||y|=Φ(x)Φ(y)$, for every $x,y∈\mathbb{R}^∗$. Moreover, $Φ$ is clearly onto (so $Φ(\mathbb{R}^∗)=\mathbb{R}^+$), and has

$\text{Ker}⁡Φ=\{x∈\mathbb{R}R^∗:Φ(x)=1\}=\{1,−1\}=N$.

Thus, $\mathbb{R}^∗/N≅\mathbb{R}^+$, by the First Isomorphism Theorem.

3. Let $n\in \mathbb{Z}^+$ and let $H=\{A\in GL(n,\mathbb{R})\,:\, \det A =\pm 1\}\text{.}$ Identify a group familiar to us that is isomorphic to $GL(n,\mathbb{R})/H\text{.}$

Solution

Define $Φ:GL(n,\mathbb{R})→\mathbb{R}^+$ by $Φ(A)=|\text{det }A|$. We have that $Φ$ is an epimorphism since for all $A,B∈GL(n,\mathbb{R})$,

$Φ(AB)=|\text{det }AB|=|\text{det }A\text{det }B|=|\text{det }A||\text{det }B|=Φ(A)Φ(B)$,

and for all $λ∈\mathbb{R}^+$, the diagonal matrix having $λ$ in the uppermost left position and $1$'s elsewhere down the diagonal gets sent to $λ$. Since $\text{Ker}⁡Φ=H$, we have that $GL(n,\mathbb{R})/H≃\mathbb{R}^+$, by the First Isomorphism Theorem.

4. Let $G$ and $G'$ be groups with respective normal subgroups $N$ and $N'\text{.}$ Prove or disprove: If $G/N\simeq G'/N'$ then $G\simeq G'\text{.}$

Solution

The statement is false. Indeed, using the preceding two problems, we see that $\mathbb{R}^∗/\{1,−1\}$ and $GL(2,\mathbb{R})/H$, where $H=\{A∈GL(2,\mathbb{R}):\text{det }A=±1\}$, are both isomorphic to $\mathbb{R}^+$, hence are isomorphic to each other. But we know that $\mathbb{R}^∗≄GL(2,\mathbb{R})$.

\(+\)	\(0\)	\(1\)	\(2\)	\(3\)
\(0\)	\(0\)	\(1\)	\(2\)	\(3\)
\(1\)	\(1\)	\(2\)	\(3\)	\(0\)
\(2\)	\(2\)	\(3\)	\(0\)	\(1\)
\(3\)	\(3\)	\(0\)	\(1\)	\(2\)

\(\cdot s\)	\(1\)	\(3\)	\(5\)	\(7\)
\(1\)	\(1\)	\(3\)	\(5\)	\(7\)
\(3\)	\(3\)	\(5\)	\(7\)	\(1\)
\(5\)	\(5\)	\(7\)	\(1\)	\(3\)
\(7\)	\(7\)	\(1\)	\(3\)	\(5\)