3.1: Generating Sets
- Page ID
- 691
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We have now seen a few different kinds of groups: groups of symmetries of a geometric object, integers under addition, integers modulo \(n\), and permutations. We can easily visualize the objects related to the group - like the geometric object, numbers, or the braid notation for permutations - but how can we visualize the group itself?
An excellent way to go about this is to identify a set of generators for the group. In a group we can always combine some elements using the group operation to get another group element. Generators are some special elements that we pick out which can be used to get to any other element in the group.
As an example, remember the dihedral group, the symmetries of an \(n\)-sided polygon. There are \(2n\) symmetries in all, but we can build up any of the symmetries using just a small rotation and a flip. For the symmetries of the equilateral triangle, we let \(\rho\) denote the rotation by \(120\) degrees, and let \(f\) be the flip over one of the axes of the triangle. Then the six elements of the dihedral group are given by: \(id, \rho, \rho^2, f, f\rho, f\rho^2\). Thus, \(\{f, \rho\}\) is a set of generators for the dihedral group.
Here's the formal definition:
Let \(G\) be a group, and \(S\) a subset of \(G\). We say that \(S\) generates \(G\) (and that \(S\) is a set of generators for \(G\)) if every element of \(G\) can be expressed as a product of elements of \(S\) and their inverses.
We include the inverses of the generators in the definition because we know that every element has an inverse. If we think of the integers under addition, we can write every positive number as a many-times sum of the number \(1\): for example, \(5\) is just \(1+1+1+1+1\). If we allow inverses as well, we can then get every element of the group from a single generator: the inverse of \(1\) is \(-1\), so we can write (for example) \(-4=(-1)+(-1)+(-1)+(-1)\). (Including the inverses also means we don't need to include the identity, since for any \(g\), \(gg^{-1}=e\).)
On the other hand, for any group \(G\), we can certainly take \(G\) itself as a generating set! Then every element is considered a 'generator,' so every element can be written as a (trivial) product of generators. This tells us that for any group we can find a generating set. Usually, we try to find a generating set as small as possible. Sometimes, though, a larger generating set might be interesting if it helps us to better understand the group in question.
Once we have a generating set for a graph \(G\), we can produce a very nice visualization of the group called the Cayley graph. By graph, we mean a number of points (called vertices) connected by some arrows (called edges). Graphs are good for keeping track of relationships between things, and appear in many, many places in mathematics and in applications.
The Cayley graph of a group has one vertex for each element \(x\) in the group. Each vertex has one arrow coming out of it for each generator \(g\), pointing to the element \(gx\). (This creates the left Cayley graph. The right Cayley graph has arrows pointing from \(x\) to \(xg\).) Usually we make the arrows different colors to correspond to the different generators; this is very useful for being able to visualize the structure of the group!
For the dihedral group, we found a set of generators with two elements: the rotation and the flip over one of the axes. In fact, the dihedral group has many different sets of generators of size two! We could have chosen the clockwise rotation instead of the counter-clockwise rotation, for example. Or we could have chosen any of the other flips. But the resulting Cayley graph would have been more-or-less the same.
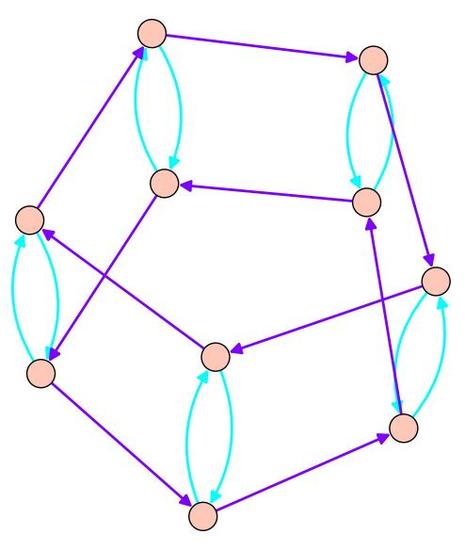
Figure 3.1: Dihedral group Cayley graph, generated by a flip and rotation.
A quite different set of generators for the dihedral group is to take two different flips, across axes that are adjacent to one another. Let's call them \(f_1\) and \(f_2\). You can actually still write any element of the dihedral group as a product of these two flips. And the resulting Cayley graph looks quite different.
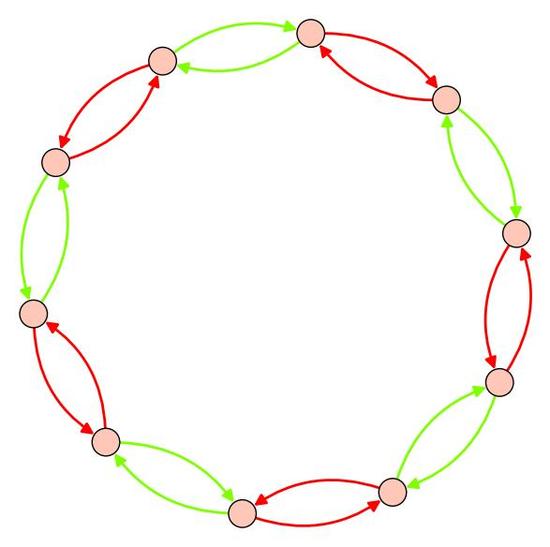
Figure. 3.2: The Cayley graph for the dihedral group with generators given by two different flips.
Suppose we have a generator where \(g^2=1\). It's tedious to draw arrows in both directions from every element, so we sometimes omit the arrow heads in this case.
Identify generators for the permutation group \(S_3\). Make a Cayley graph.
Contributors and Attributions
- Tom Denton (Fields Institute/York University in Toronto)


