1.3: Stereographic Projection

Stereographic projection \(S^1\to \hat{\mathbb{R}}\)

Let \(S^1\) denote the unit circle in the \(x,y\)-plane.

\[
S^1 = \{(x,y)\in \mathbb{R}^2 \colon x^2+y^2=1\}\label{s1defn}\tag{1.3.1}
\]

Let \(N=(0,1)\) denote the "north pole" (that is, the point at the "top" of the unit circle). Given a point \(P=(x,y)\neq N\) on the unit circle, let \(s(P)\) denote the intersection of the line \(\overline{NP}\) with the \(x\)-axis. See Figure 1.3.1. The map \(s\colon S^1\setminus \{N\}\to \mathbb{R}\) given by this rule is called stereographic projection. Using similar triangles, it is easy to see that \(s(x,y)=\frac{x}{1-y}\text{.}\)

Figure 1.3.1. Stereographic projection

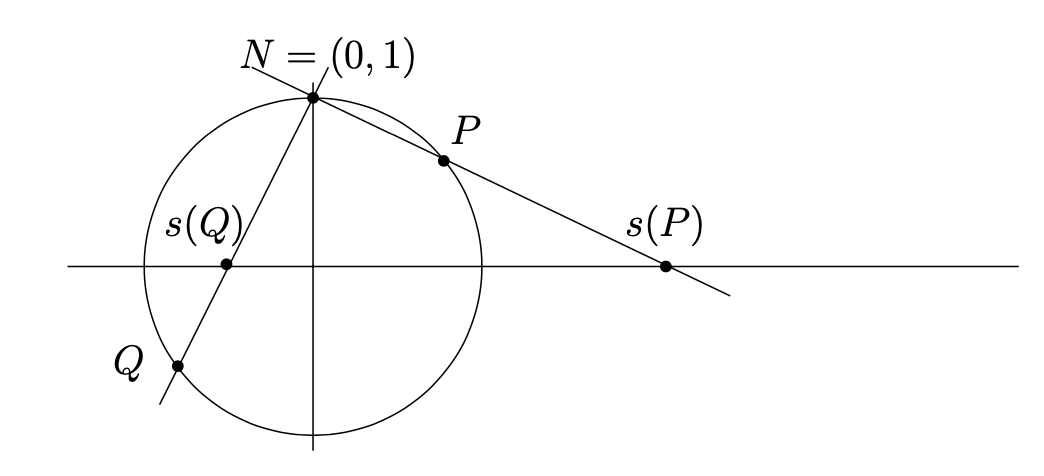
Checkpoint 1.3.2.

Draw the relevant similar triangles and verify the formula \(s(x,y) = \frac{x}{1-y}\text{.}\)

We extend stereographic projection to the entire unit circle as follows. We call the set

\[\hat{\mathbb{R}}=\mathbb{R}\cup \{\infty\}\label{extendedrealsdefn}\tag{1.3.2}\]

the extended real numbers, where "\(∞\)" is an element that is not a real number. Now we define stereographic projection \(s\colon S^1 \to \hat{\mathbb{R}}\) by

\[s(x,y) = \left\{
\begin{array}{cc}
\frac{x}{1-y} & y\neq 1\\
\infty & y=1
\end{array}
\right..\label{stereoproj1defn}\tag{1.3.3}\]

Stereographic projection \(S^2\to \hat{\mathbb{C}}\)

The definitions in the previous subsection extend naturally to higher dimensions. Here are the details for the main case of interest.

Let \(S^2\) denote the unit sphere in \(\mathbb{R}^3\text{.}\)

\[
S^2 = \{(a,b,c)\in \mathbb{R}^3\colon a^2+b^2+c^2=1\}\label{s2defn}\tag{1.3.4}
\]

Let \(N=(0,0,1)\) denote the "north pole" (that is, the point at the "top" of the sphere, where the positive \(z\)-axis is "up"). Given a point \(P=(a,b,c)\neq N\) on the unit sphere, let \(s(P)\) denote the intersection of the line \(\overline{NP}\) with the \(x,y\)-plane, which we identify with the complex plane \(\mathbb{C}\). See See Figure 1.3.3. The map \(s\colon S^2\setminus \{N\}\to \mathbb{C}\) given by this rule is called stereographic projection. Using similar triangles, it is easy to see that \(s(a,b,c)=\frac{a+ib}{1-c}\text{.}\)

Figure 1.3.3. Stereographic projection

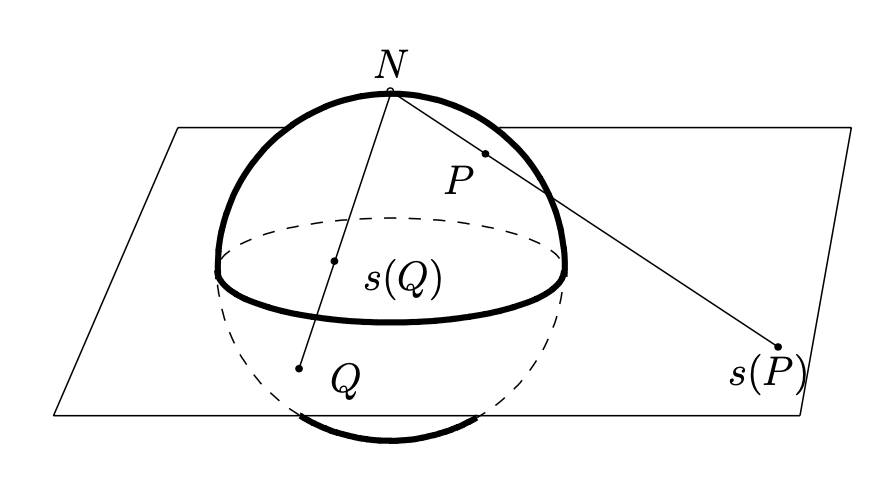
We extend stereographic projection to the entire unit sphere as follows. We call the set

\[\hat{\mathbb{C}}=\mathbb{C}\cup \{\infty\}\label{extendedcomplexsdefn}\tag{1.3.5}\]

the extended complex numbers, where "\(∞\)" is an element that is not a complex number. Now we define stereographic projection \(s\colon S^2 \to \hat{\mathbb{C}}\) by

\[s(a,b,c) = \left\{
\begin{array}{cc}
\frac{a+ib}{1-c} & c\neq 1\\
\infty & c=1
\end{array}
\right..\label{stereoprojdefn}\tag{1.3.6}
\]

Exercises

Formulas for inverse stereographic projection.

It is intuitively clear that stereographic projection is a bijection. Make this rigorous by finding a formula for the inverse.

Exercise 1

For \(s\colon S^1\to \hat{\mathbb{R}}\text{,}\) find a formula for \(s^{-1}\colon \hat{\mathbb{R}}\to S^1\text{.}\) Find \(s^{-1}(3)\text{.}\)

Answer

\[
s^{-1}(r) = \begin{cases}
\left(\frac{2r}{r^2+1},\frac{r^2-1}{r^2+1}\right) &
\text{ if } r\neq \infty\\ (0,1)& \text{ if } r=\infty
\end{cases}
\nonumber \]

\(s^{-1}(3) = (3/5,4/5)\)

Exercise 2

For \(s\colon S^2\to \hat{\mathbb{C}}\text{,}\) find a formula for \(s^{-1}\colon \hat{\mathbb{C}}\to S^2\text{.}\) Find \(s^{-1}(3+i)\text{.}\)

Answer

\[
s^{-1}(z) = \begin{cases}
\left(\frac{2Re(z)}{|z|^2+1},\frac{2Im(z)}{|z|^2+1},
\frac{|z|^2-1}{|z|^2+1}\right)& \text{ if } z\neq
\infty\\ (0,0,1) & \text{ if } z=\infty \end{cases}
\nonumber \]

\(s^{-1}(3+i) = (6/11,2/11,9/11)\)

Conjugate transformations.

Let \(\mu \colon X\to Y\) be a bijective map. We say that maps and \(f\colon X\to X\) and \(g\colon Y\to Y\) are conjugate transformations (with respect to the bijection \(\mu\)) if \(f = \mu^{-1}\circ g\circ \mu\text{.}\)

Exercise 3

Show that the maps \(S^1\to S^1\) given by \((x,y)\to (x,-y)\) and \(\hat{\mathbb{R}}\to \hat{\mathbb{R}}\) given by \(x\to 1/x\) are conjugate transformations with respect to stereographic projection

Exercise 4

Show that the map \(R_{Z,\theta}\colon S^2\to S^2\) given by \((a,b,c)\to
(a\cos\theta-b\sin\theta,a\sin\theta+b\cos\theta,c)\) (a rotation about the \(z\)-axis by angle \(θ\)) and the map \(T_{Z,\theta}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}\) given by \(z\to e^{i\theta}z\) are conjugate transformations with respect to stereographic projection.

Exercise 5

Show that the map \(R_{X,\pi}\colon S^2\to S^2\) given by \((a,b,c)\to (a,-b,-c)\) (rotation about the \(x\)-axis by \(\pi\) radians) and the map \(T_{X,\pi}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}\) given by \(z\to 1/z\) are conjugate transformations with respect to stereographic projection.

Exercise 6

Show that the map \(R_{X,\pi/2}\colon S^2\to S^2\) given by \((a,b,c)\to (a,-c,b)\) (rotation about the \(x\)-axis by \(\pi/2\) radians) and the map \(T_{X,\pi/2}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}\) given by \(z\to \frac{z+i}{iz+1}\) are conjugate transformations with respect to stereographic projection.

7. Projections of endpoints of diameters.

Show that \(s(a,b,c)(s(-a,-b,-c))^\ast=-1\) for any point \((a,b,c)\) in \(S^2\) with \(|c|\neq 1\text{.}\) Conversely, suppose that \(zw^\ast=-1\) for some \(z,w\in \mathbb{C}\text{.}\) Show that .