1.3: Stereographic Projection

Stereographic projection $S^1\to \hat{\mathbb{R}}$

Let $S^1$ denote the unit circle in the $x,y$-plane.

$$S^1 = \{(x,y)\in \mathbb{R}^2 \colon x^2+y^2=1\}\label{s1defn}\tag{1.3.1}$$

Let $N=(0,1)$ denote the "north pole" (that is, the point at the "top" of the unit circle). Given a point $P=(x,y)\neq N$ on the unit circle, let $s(P)$ denote the intersection of the line $\overline{NP}$ with the $x$-axis. See Figure 1.3.1. The map $s\colon S^1\setminus \{N\}\to \mathbb{R}$ given by this rule is called stereographic projection. Using similar triangles, it is easy to see that $s(x,y)=\frac{x}{1-y}\text{.}$

Figure 1.3.1. Stereographic projection

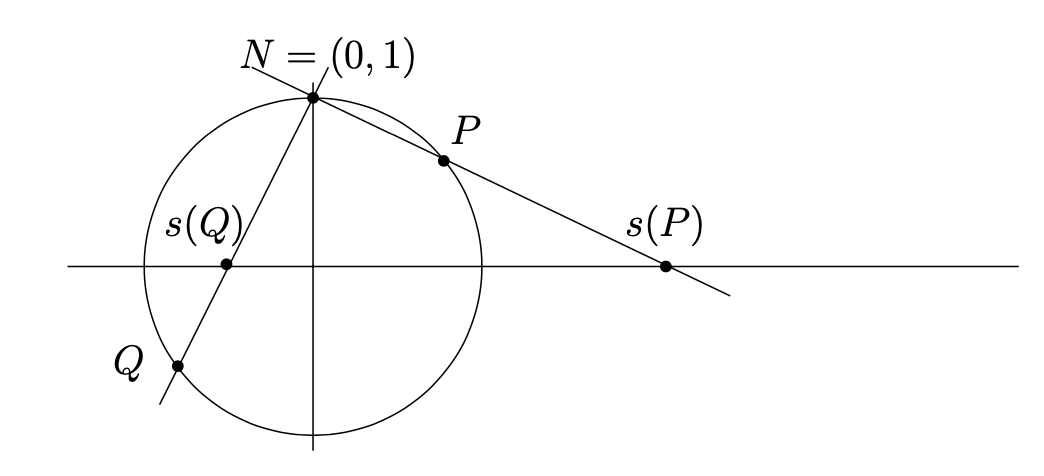
Checkpoint 1.3.2.

Draw the relevant similar triangles and verify the formula $s(x,y) = \frac{x}{1-y}\text{.}$

We extend stereographic projection to the entire unit circle as follows. We call the set

$$\hat{\mathbb{R}}=\mathbb{R}\cup \{\infty\}\label{extendedrealsdefn}\tag{1.3.2}$$

the extended real numbers, where "$∞$" is an element that is not a real number. Now we define stereographic projection $s\colon S^1 \to \hat{\mathbb{R}}$ by

$$s(x,y) = \left\{ \begin{array}{cc} \frac{x}{1-y} & y\neq 1\\ \infty & y=1 \end{array} \right..\label{stereoproj1defn}\tag{1.3.3}$$

Stereographic projection $S^2\to \hat{\mathbb{C}}$

The definitions in the previous subsection extend naturally to higher dimensions. Here are the details for the main case of interest.

Let $S^2$ denote the unit sphere in $\mathbb{R}^3\text{.}$

$$S^2 = \{(a,b,c)\in \mathbb{R}^3\colon a^2+b^2+c^2=1\}\label{s2defn}\tag{1.3.4}$$

Let $N=(0,0,1)$ denote the "north pole" (that is, the point at the "top" of the sphere, where the positive $z$-axis is "up"). Given a point $P=(a,b,c)\neq N$ on the unit sphere, let $s(P)$ denote the intersection of the line $\overline{NP}$ with the $x,y$-plane, which we identify with the complex plane $\mathbb{C}$. See See Figure 1.3.3. The map $s\colon S^2\setminus \{N\}\to \mathbb{C}$ given by this rule is called stereographic projection. Using similar triangles, it is easy to see that $s(a,b,c)=\frac{a+ib}{1-c}\text{.}$

Figure 1.3.3. Stereographic projection

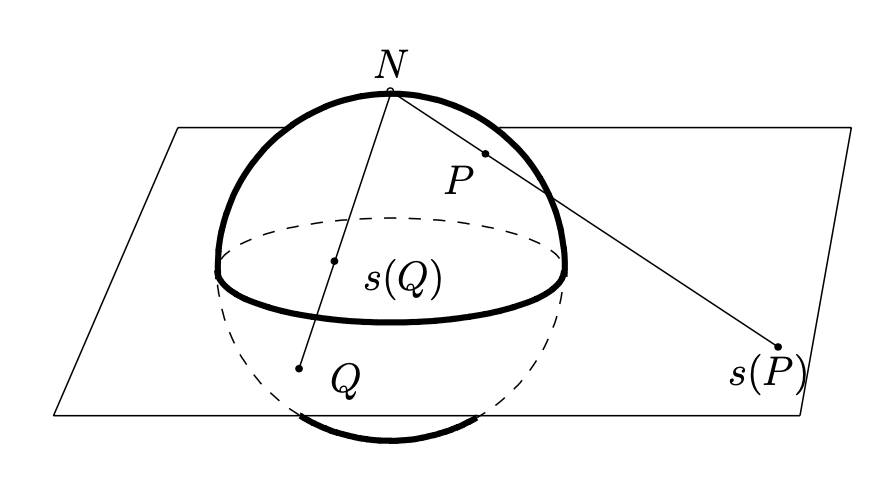
We extend stereographic projection to the entire unit sphere as follows. We call the set

$$\hat{\mathbb{C}}=\mathbb{C}\cup \{\infty\}\label{extendedcomplexsdefn}\tag{1.3.5}$$

the extended complex numbers, where "$∞$" is an element that is not a complex number. Now we define stereographic projection $s\colon S^2 \to \hat{\mathbb{C}}$ by

$$s(a,b,c) = \left\{ \begin{array}{cc} \frac{a+ib}{1-c} & c\neq 1\\ \infty & c=1 \end{array} \right..\label{stereoprojdefn}\tag{1.3.6}$$

Exercises

Formulas for inverse stereographic projection.

It is intuitively clear that stereographic projection is a bijection. Make this rigorous by finding a formula for the inverse.

Exercise 1

For $s\colon S^1\to \hat{\mathbb{R}}\text{,}$ find a formula for $s^{-1}\colon \hat{\mathbb{R}}\to S^1\text{.}$ Find $s^{-1}(3)\text{.}$

Answer

$$s^{-1}(r) = \begin{cases} \left(\frac{2r}{r^2+1},\frac{r^2-1}{r^2+1}\right) & \text{ if } r\neq \infty\\ (0,1)& \text{ if } r=\infty \end{cases} \nonumber$$

$s^{-1}(3) = (3/5,4/5)$

Exercise 2

For $s\colon S^2\to \hat{\mathbb{C}}\text{,}$ find a formula for $s^{-1}\colon \hat{\mathbb{C}}\to S^2\text{.}$ Find $s^{-1}(3+i)\text{.}$

Answer

$$s^{-1}(z) = \begin{cases} \left(\frac{2Re(z)}{|z|^2+1},\frac{2Im(z)}{|z|^2+1}, \frac{|z|^2-1}{|z|^2+1}\right)& \text{ if } z\neq \infty\\ (0,0,1) & \text{ if } z=\infty \end{cases} \nonumber$$

$s^{-1}(3+i) = (6/11,2/11,9/11)$

Conjugate transformations.

Let $\mu \colon X\to Y$ be a bijective map. We say that maps and $f\colon X\to X$ and $g\colon Y\to Y$ are conjugate transformations (with respect to the bijection $\mu$) if $f = \mu^{-1}\circ g\circ \mu\text{.}$

Exercise 3

Show that the maps $S^1\to S^1$ given by $(x,y)\to (x,-y)$ and $\hat{\mathbb{R}}\to \hat{\mathbb{R}}$ given by $x\to 1/x$ are conjugate transformations with respect to stereographic projection

Exercise 4

Show that the map $R_{Z,\theta}\colon S^2\to S^2$ given by $(a,b,c)\to (a\cos\theta-b\sin\theta,a\sin\theta+b\cos\theta,c)$ (a rotation about the $z$-axis by angle $θ$) and the map $T_{Z,\theta}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}$ given by $z\to e^{i\theta}z$ are conjugate transformations with respect to stereographic projection.

Exercise 5

Show that the map $R_{X,\pi}\colon S^2\to S^2$ given by $(a,b,c)\to (a,-b,-c)$ (rotation about the $x$-axis by $\pi$ radians) and the map $T_{X,\pi}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}$ given by $z\to 1/z$ are conjugate transformations with respect to stereographic projection.

Exercise 6

Show that the map $R_{X,\pi/2}\colon S^2\to S^2$ given by $(a,b,c)\to (a,-c,b)$ (rotation about the $x$-axis by $\pi/2$ radians) and the map $T_{X,\pi/2}\colon \hat{\mathbb{C}}\to \hat{\mathbb{C}}$ given by $z\to \frac{z+i}{iz+1}$ are conjugate transformations with respect to stereographic projection.

7. Projections of endpoints of diameters.

Show that $s(a,b,c)(s(-a,-b,-c))^\ast=-1$ for any point $(a,b,c)$ in $S^2$ with $|c|\neq 1\text{.}$ Conversely, suppose that $zw^\ast=-1$ for some $z,w\in \mathbb{C}\text{.}$ Show that .