1.1: Complex Numbers

The complex numbers were originally invented to solve problems in algebra. It was later recognized that the algebra of complex numbers provides an elegant set of tools for geometry in the plane. This section presents the basics of the algebra and geometry of the complex numbers.

Elements in the set of complex numbers \(\mathbb{C}\) are in one-to-one correspondence with points in the 2-dimensional real plane \(\mathbb{R}^{2}\) (where \(\mathbb{R}\) denotes the set of real numbers). We will write \(z\leftrightarrow (x,y)\) to denote that the complex number \(z\) corresponds to the ordered pair \((x,y)\) of real numbers.

Real and imaginary parts

Given a complex number \(z\) corresponding to the point \((x,y)\) in \(\mathbb{R}^{2}\), we say that \(x\) is the real part of \(z\) and that \(y\) is the imaginary part of \(z\), denoted \(Re\left ( z \right )=x\) and \(Im⁡(z)=y\). The set \(\mathbb{C}\) contains the set \(\mathbb{R}\) as a subset. The real number \(x\), which is also the complex number \(x\), corresponds to the ordered pair \((x,0)\). A complex number that corresponds to an ordered pair \((0,y)\) is called (pure) imaginary. The complex number i corresponds to the ordered pair \((0,1)\). Here is a summary so far.

\begin{align*}
z & \leftrightarrow (Re\left ( z \right ),Im\left ( z \right ))\\
x\in\mathbb{R}& \leftrightarrow (x,0)\\
i & \leftrightarrow (0,1)
\end{align*}

Modulus and argument

Figure 1.1.1. Norm and argument of a complex number are polar coordinates.

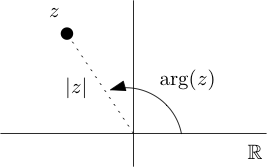
Given a complex number \(z\leftrightarrow (x,y)\text{,}\) let \((r,\theta)\) be polar coordinates for the point \((x,y)\) such that \(r≥0\) and \(θ\) is measured in radians. The modulus or norm of \(z\text{,}\) denoted \(|z|\), is defined to be the polar coordinate \(r=\sqrt{x^2+y^2}\) and the argument of \(z\text{,}\) denoted \(\arg(z)\), is the polar coordinate \(θ\), that is, the oriented angle made by the real vector \((x,y)\) with the positive real axis. In other words, \((|z|,\arg{z})\) are polar coordinates for the point \((x,y)\text{.}\) See Figure 1.1.1. Here is a summary.

Norm and argument.

\[
z\leftrightarrow (x,y) = \left(|z|\cos( \arg{z}),|z|\sin(\arg{z})\right) \label{normargdef}\tag{1.1.1}
\]

Addition and multiplication of complex numbers

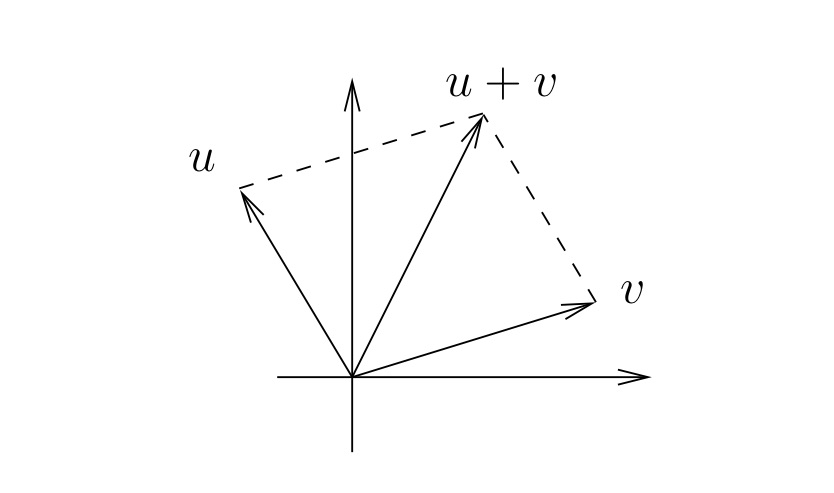
Given complex numbers \(z\leftrightarrow (x,y)\) and \(z'\leftrightarrow(x',y')\text{,}\) the sum \(z+z'\) is defined by the following.

Complex addition.

\[
z+z' \leftrightarrow (x+x',y+y')\label{complexadddef}\tag{1.1.2}
\]

In other words, complex addition corresponds to real vector addition. See Figure 1.1.2.

Figure 1.1.2. Complex addition is vector addition

The product \(zz'\) is defined as follows.

Complex multiplication.

\begin{align}
|zz'| & = |z||z'|\label{complexmultdefnorm}\tag{1.1.3}\\
\arg(zz') & = \arg{z}+\arg{z'}\label{complexmultdefarg}\tag{1.1.4}
\end{align}

The interaction between complex addition and multiplication is expressed by the following relationship, which holds for any complex \(z,u,v\text{.}\) See Figure 1.1.3.

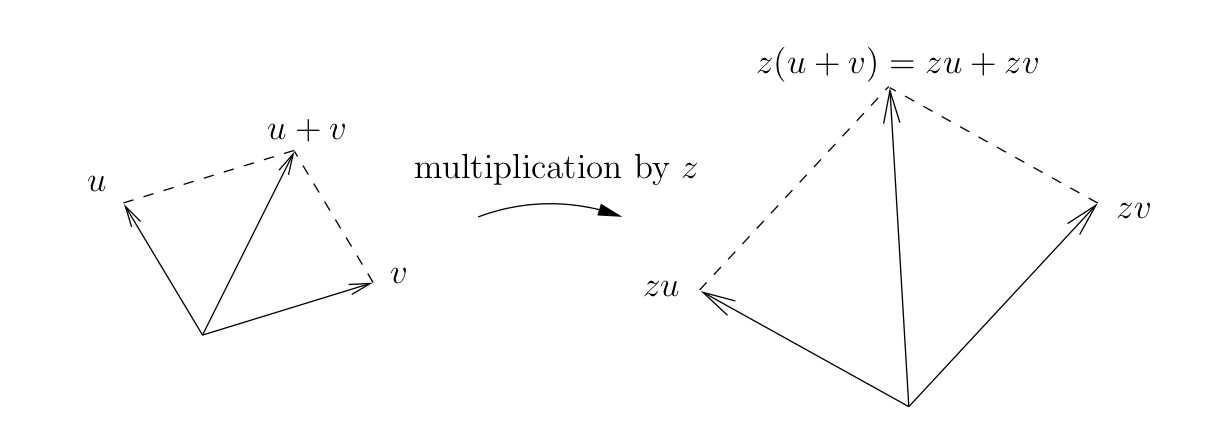
Distributive law.

\[
z(u+v) = zu+zv \label{distributivelaw}\tag{1.1.5}
\]

Figure 1.1.3. The distributive law: multiplication by \(z\) rotates the vectors \(u\text{,}v\text{,}\) and \(u+v\) by angle \(\arg z\) and scales by the factor \(|z|\text{.}\)

Below are a number of relationships arising from the definitions of complex addition and multiplication. Let \(a,b,c,d\) be real numbers and let \(z,u,v\) be complex numbers. The following relationships hold. ¹

\begin{align}
a+ib & \leftrightarrow (a,b)\tag{1.1.6}\\
a+b \;\;\text{(complex sum)} &= a+b \;\;\text{(real sum)}\label{addextends}\tag{1.1.7}\\
ab \;\;\text{(complex product)} & = ab \;\;\text{(real product)}\label{multextends}\tag{1.1.8}\\
|a| \;\;\text{(complex norm)} & = |a| \;\;\text{(real absolute value)}\label{normextends}\tag{1.1.9}\\
1z & = z1 = z \label{multidentity}\tag{1.1.10}\\
i^2 & = -1\label{i2isminus1}\tag{1.1.11}\\
(a+ib)+ (c+id) & = (a+c) + i(b+d)\tag{1.1.12}\\
(a+ib)(c+id) & = (ac-bd) + i(ad+bc)\label{complexmultrectangular}\tag{1.1.13}
\end{align}

The complex exponential function

The Taylor series for the real function \(y=e^x\) is

\[
e^x = 1 +x +\frac{x^2}{2} +\frac{x^3}{3!} + \cdots .
\nonumber \]

Convergence for sequences and series of complex numbers can be defined in a way that naturally extends the definitions for real numbers. It turns out that the complex power series

\[
1 +z +\frac{z^2}{2} +\frac{z^3}{3!} + \cdots
\nonumber \]

converges for every complex number \(z\text{,}\) so we define the complex exponential function by

\[
e^z= 1 +z +\frac{z^2}{2} +\frac{z^3}{3!} + \cdots .
\nonumber \]

The complex exponential obeys familiar laws of the real exponential. For \(z,w\) in \(\mathbb{C}\), we have

\begin{align*}
e^ze^w & = e^{z+w}\\
e^0 & =1
\end{align*}

A key property of the complex exponential is the following, called Euler's formula.

Euler's formula.

\[
e^{it}= \cos t + i\sin t \;\;\text{(for $t$ real)}\label{eulersformula}\tag{1.1.14}
\]

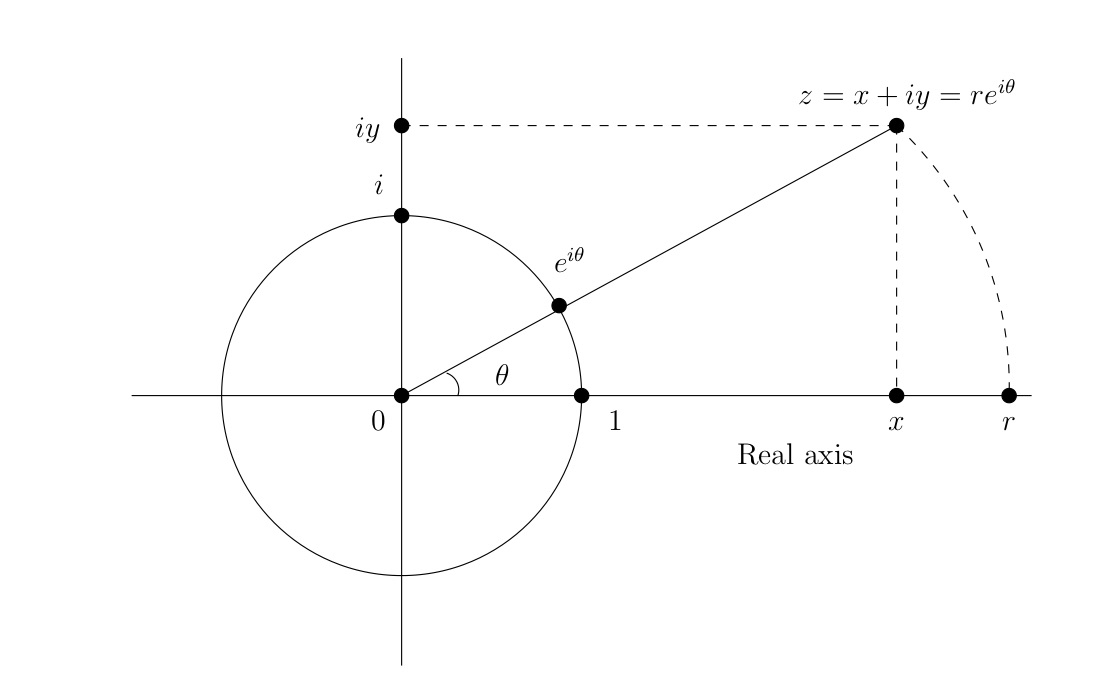
For \(z\) with \(r=|z|\) and \(t=\arg(z)\text{,}\) the expression \(z=re^{it}\) is called the polar form for \(z\text{.}\) By contrast, we call \(z=x+iy\) the rectangular form (or the Cartesian form ) for \(z\text{.}\) Figure 1.1.4 shows a summary of the geometric content of the rectangular and polar forms for a complex number \(z\text{.}\)

Here is how complex multiplication looks in polar form. For \(z=re^{i\theta}, w=se^{i\phi}\text{,}\) we have

\[
zw = (re^{i\theta})(se^{i\phi}) = rse^{i(\theta + \phi)}.\label{complexmultpolar}\tag{1.1.15}
\]

From this it is easy to see that for \(r\neq 0\text{,}\) we have

\[
\left(re^{i\theta}\right)\; \left(\frac{1}{r}e^{-i\theta}\right) = 1.
\nonumber \]

For \(z=re^{i\theta}\) with \(r\neq 0\text{,}\) we call \(\frac{1}{r}e^{-i\theta}\) the multiplicative inverse of \(z\text{,}\) denoted \({1}/{z}\)or \(z^{-1}\text{.}\)

Figure 1.1.4. Rectangular and polar forms for a complex number \(z\)

Conjugation

The conjugate of the complex number \(z=x+iy=re^{i\theta}\text{,}\) denoted \(\overline{z}\) or \(z^\ast\), is defined to be \(z^\ast = x-iy = re^{-i\theta}\text{.}\) Geometrically, \(z^\ast\) is the reflection of \(z\) across the real axis (the \(x\)-axis) in \(\mathbb{R}^{2}\). Here are some relations involving conjugates.

\begin{align}
Re(z) & = \frac{z + z^\ast}{2}\label{realpartformula}\tag{1.1.16}\\
Im(z) & = \frac{z - z^\ast}{2i}\label{imagpartformula}\tag{1.1.17}\\
|z|^2 & = zz^\ast\label{zzbarisnormsq}\tag{1.1.18}\\
2\arg z & = \frac{z}{z^\ast} \;\;\text{(for $z\neq 0$)}\tag{1.1.19}\\
\frac{1}{z}
& = \frac{z^\ast}{zz^\ast}= \frac{z^\ast}{|z|^2} \;\;\text{(for $z\neq 0$)}\tag{1.1.20}\\
(zw)^\ast & = z^\ast w^\ast\tag{1.1.21}
\end{align}

Circles and lines

Let \(C\) be the circle of radius \(r\gt 0\) and with center \(a\in \mathbb{C}\text{.}\) A point \(z\) lies on \(C\) if and only if the distance from \(z\) to a equals \(r\text{.}\) In mathematical symbols, \(C\) is the set of solutions \(z\) for the following equation.

\[
|z-a|=r\label{circleeqn}\tag{1.1.22}
\]

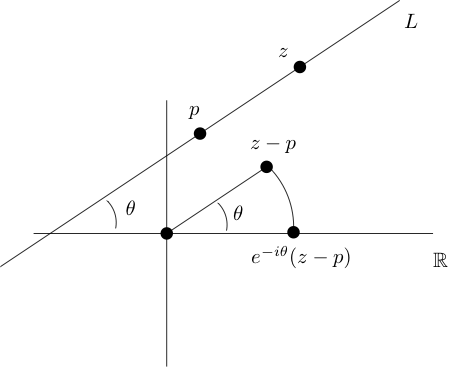
The real line \(\mathbb{R}\) is the set of solutions \(z\) of the equation \(Im⁡(z)=0\). More generally, let \(L\) be a line that contains the point \(p\in \mathbb{C}\) and makes an angle \(\theta\) with the real axis (set \(\theta=0\)if \(L\) is parallel to the real axis). If \(z\in L\text{,}\) then \(e^{-i\theta}(z-p)\) is real, so \(Im(e^{-i\theta}(z-p))=0\text{.}\) See Figure 1.1.5. Conversely, if \(e^{-i\theta}(z-p)\) is real, then \(z\) lies on \(L\text{.}\) Multiplying by a positive constant \(k\text{,}\) and setting \(a=ke^{-i\theta}\) and ,\(b=-ke^{-i\theta}p\text{,}\) we conclude that the line \(L\) is the set of solutions to the following equation.

\[
Im(az+b)=0\label{lineeqn}\tag{1.1.23}
\]

Figure 1.1.5. A line in the complex plane.

Exercises

Exercise 1

What is the difference between polar coordinates and polar form? What is the difference between rectangular coordinates and rectangular form? Write formulas for converting from polar to rectangular coordinates and vice-versa.

Solution

Let \(z\) be a complex number, let \(x=Re(z)\text{,}\) \(y=Im(z)\text{,}\) \(r=|z|\) and \(\theta = \arg(z)\text{.}\) The pair \((r,θ)\) is called the polar coordinates for \(z\text{,}\) while the expression \(re^{i\theta}\) is called the polar form for \(z\text{.}\) The pair \((x,y)\) is called the rectangular coordinates for \(z\text{,}\) while the expression \(x+iy\) is called the rectangular form for \(z\text{.}\)

To convert from polar to rectangular, use the equations \(x=r\cos \theta, y=r\sin \theta\) (show sketches to explain these formulas). To convert from rectangular to polar, use \(r=\sqrt{x^2+y^2}\) and \(\tan \theta = y/x\text{.}\) For the last equation, you must use judgment when \(x=0\) to decide whether \(θ\) should be \(\pi/2\) or \(-\pi/2\text{.}\) You must also use judgment when calculating \(\theta = \arctan (y/x)\text{.}\) The standard codomain for arctan is the interval \((\pi/2,\pi/2)\text{,}\) so you need to use \(\theta = \arctan (y/x) + \pi\) for \(x\lt 0\text{.}\)

Exercise 2

Express each of the following in rectangular and polar form.

a. \(\displaystyle 3(2-i) + 6(1+i)\)

b. \(\displaystyle \left(2e^{i\pi/6}\right)\left(3e^{-i\pi/3}\right)\)

c. \(\displaystyle (2+3i)(4-i)\)

d. \(\displaystyle (1+i)^3\)

Answer

a. \(\displaystyle 12+3i=\sqrt{153}\;e^{i\arctan(1/4)}\)

b. \(\displaystyle 6e^{-i\pi/6}=3\sqrt{3}-3i\)

c. \(\displaystyle 11+10i=\sqrt{221}\;e^{i\arctan(10/11)}\)

d. \(\displaystyle -2+2i=2\sqrt{2}\;e^{i3\pi/4}\)

Exercise 3

Prove the following property of norm.

The triangle inequality.

For any two complex numbers \(z,w\text{,}\) we have

\(\[
|z+w|\leq |z|+|w|.
\nonumber \]\)

Solution

The simplest approach is geometric: Sketch the parallelogram for vector addition and use the fact that the length of any side of a triangle is less than the sum of the lengths of the other two sides.

Here is one route to an algebraic proof: Let \(z=a+bi\text{,}\) \(w=c+di\text{.}\) Manipulate the triangle inequality (start by squaring both sides) to obtain

\(\[
2abcd \leq b^2c^2 + a^2d^2.
\nonumber \]\)

This is the same as the clearly true statement

\[
0\leq b^2c^2 + a^2d^2 - 2abcd = (bc-ad)^2.
\nonumber \]

Conclude by observing that all steps of the derivation are reversible.

Exercise 4

Prove (1.1.18).

Solution

Let \(z=re^{i\theta}\text{.}\) Then \(\overline{z}=re^{-i\theta}\text{,}\) and we have

\begin{align*}
z\overline{z} & = re^{i\theta}re^{-i\theta}\\
& = r^2 e^0\\
& = r^2 = |z|^2.
\end{align*}

Exercise 5

Let \(p\) and \(q\) be complex numbers. Prove that the distance (ordinary distance between points in the plane) between \(p\) and \(q\) is \(|p-q|\text{.}\)

Hint

Use rectangular form.

Solution

Let \(p=a+ib\) and \(q=c+id\text{.}\) We have

\begin{align*}
|p-q| & = |(a+ib)-(c+id)| \\
& = |(a-c)+i(b-d)|\\
& = \sqrt{(a-c)^2 + (b-d)^2}.
\end{align*}

The latter expression is the distance from \(p\) to \(q\text{,}\) so we are done.

Exercise 6

Express each of the following in rectangular and polar form.

a. \(\displaystyle \displaystyle \frac{2+i}{3-i}\)

b. \(\displaystyle \displaystyle \frac{1+2i}{1-2i}\)

c. \(\displaystyle \displaystyle \frac{2e^{i\pi/4}}{3e^{-i\pi/2}}\)

Answer

a. \(\displaystyle \displaystyle \frac{1}{2} + \frac{1}{2}i=\frac{\sqrt{2}}{2}e^{i\pi/4}\)

b. \(\displaystyle \displaystyle -\frac{3}{5} +\frac{4}{5}i=e^{i(\arctan(-4/3)+\pi)}\)

c. \(\displaystyle \displaystyle \frac{2}{3}e^{i3\pi/4}=-\frac{\sqrt{2}}{3} + \frac{\sqrt{2}}{3}i\)

Exercise 7

Verify the formulas (1.1.16) and (1.1.17).

Solution

Let \(z=x+iy\text{.}\) Then we have

• \(\displaystyle \frac{z+\overline{z}}{2}= \frac{2x}{2}=x=Re(z)\text{,}\) and
• \(\displaystyle \frac{z-\overline{z}}{2i}=\frac{2iy}{2i}=y=Im(z)\text{.}\)

Exercise 8

Given a nonzero complex number \(z\text{,}\) explain why \(z\) has exactly two square roots, and explain how to find them.

Solution

Since squaring a number squares the norm and doubles the argument, a square root can be found by taking the square root of the norm and dividing the argument by two. That is, for \(z=re^{i\theta}\text{,}\) a square root of \(z\) is \(\sqrt{r}e^{i\theta/2}\text{.}\) Another square root of \(z\) is the negative of that expression. Any other square root of \(z\) would have to have norm \(\sqrt{|z|}\) and argument \(\theta/2\) plus or minus an integer multiple of \(\pi\text{,}\) so these must be all the square roots of \(z\text{.}\)

Exercise 9

Find all complex solutions of the following equations.

a. \(\displaystyle \displaystyle z^2 + 3z + 5 = 0\)

b. \(\displaystyle (z - i)(z + i) = 1\)

c. \(\displaystyle \displaystyle \frac{2z + i}{-z+3i} = z\)

Answer

a. \(\displaystyle \displaystyle -\frac{3}{2} \pm i\frac{\sqrt{11}}{2}\)

b. \(\displaystyle 0\)

c. \(\displaystyle (1/2)[(-2 \pm 281^{1/4}\cos \varphi) + i(3 \pm 281^{1/4}\sin \varphi)]\text{,}\) where

\(\varphi=(\arctan(16/5)+\pi)/2\)

Exercise 10

Use the fact that \(e^{ia}e^{ib}=e^{i(a+b)}\) together with Euler's formula \(e^{i\theta}=\cos\theta + i\sin\theta\) to derive the trigonometric angle sum formulas below.

\begin{align*}
\cos(a+b) & = \cos a \cos b -\sin a \sin b\\
\sin(a+b) & = \cos a \sin b + \sin a \cos b
\end{align*}

Solution

Using Euler's formula for the first equality below, and then using complex multiplication for the second equality, we have

\begin{align}
e^{ia}e^{ib} & = (\cos a + i\sin a)(\cos b + i\sin b)\notag\\
& = (\cos a\cos b - \sin a \sin b) + i(\cos a \sin b + \sin a\cos b).\label{localtag1}\tag{\(\star\)}
\end{align}

On the other hand, Euler's formula also gives

\begin{gather}
e^{i(a+b)}= \cos(a+b) + i\sin
(a+b).\label{localtag2}\tag{\(\star\star\)}
\end{gather}

Equating real and and imaginary parts of (⋆) and (⋆⋆) gives the desired trigonometric identities.

Exercise 11

Circles and lines.

a. For a real variable \(x\) and a real constant \(a\text{,}\) completing the square refers to rewriting the expression \(x^2 - 2ax\) as follows.

\[
x^2-2ax = x^2-2ax +a^2 - a^2 = \left(x-a\right)^2
-a^2.
\nonumber \]

A complex version of completing the square for a complex variable z and a complex constant a is the following.

\[
|z|^2-2Re(za^\ast)=|z-a|^2
-|a|^2\label{complexcompletesquare}\tag{1.1.24}
\]

Write a derivation to justify this. Then use completing the square to find the center and radius of the circle given by the equation \(|z|^2 -iz +iz^\ast -5=0\text{.}\)

b. Write an alternative proof for the general form for the equation of a line (1.1.23), as follows. Let \(a=u+iv\text{,}\) \(b=r+is\text{,}\) \(z=x+iy\text{.}\) Find the equation of the line \(Im(az+b)=0\) in terms of the real variables \(x,y\) and real constants \(u,v,r,s\text{.}\) Explain why it is necessary that \(a\neq 0\text{.}\)

Exercise 12

Complex numbers as 2×2 real matrices.

Let \({\mathcal M}_\mathbb{C}\) denote the set of 2×2 matrices of the form \(\left[\begin{array}{cc}a& b\\-b& a\end{array}\right]\) with \(a,b\in \mathbb{R}\text{.}\) Given a complex number \(z\) with Cartesian form \(z=a+bi\text{,}\) let \(M(z)\) denote the matrix in \(\left[\begin{array}{cc}a &
b\\-b& a\end{array}\right]\) in \({\mathcal M}_\mathbb{C}\text{.}\) Conversely, given a matrix \(M\in {\mathcal M}_\mathbb{C}\) with top left entry \(a\) and top right entry \(b\text{,}\) let \(C(M)\) denote the complex number \(a+bi\text{.}\) It is clear that the mappings \(z\to M(z)\) and \(M\to C(M)\) are inverses to one another, and establish a one-to-one correspondence \(\mathbb{C}\leftrightarrow {\mathcal M}_\mathbb{C}\text{.}\)

a. Show that \({\mathcal M}_\mathbb{C}\) is closed under addition and multiplication. That is, suppose that \(M,N\) are elements of \({\mathcal M}_\mathbb{C}\text{.}\) Show that \(M+N\) and \(MN\) are also elements of \({\mathcal M}_\mathbb{C}\text{.}\)

b. Show that complex addition and multiplication are "mirrored" in \({\mathcal M}_\mathbb{C}\text{.}\) That is, show that \(C(M(z)+M(w))=z+w\) and \(C(M(z)M(w))=zw\) for all \(z,w\in \mathbb{C}\text{.}\)