Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

6.E: Solving Equations and Inequalities (Exercises)

Last updated

Oct 6, 2021
Save as PDF
- 6.6: Solving Polynomial and Rational Inequalities
- 7: Exponential and Logarithmic Functions

Anonymous
LibreTexts

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Exercise $\PageIndex{1}$

Solve by extracting the roots.

$x^{2}-81=0$
$y^{2}-\frac{1}{4}=0$
$9 x^{2}-8=0$
$5 x^{2}-12=0$
$2 y^{2}-7=0$
$3 y^{2}-6=0$
$(2 x-3)^{2}-16=0$
$4(x-1)^{2}-5=0$
$9(x-3)^{2}+4=0$
$5(2 x+1)^{2}+1=0$
$2 x^{2}+10=0$
$x^{2}+64=0$
The height in feet of an object dropped from a $20$ -foot stepladder is given by $h (t) = −16t^{2} + 20$ where $t$ represents the time in seconds after the object has been dropped. How long does it take the object to hit the ground after it has been dropped? Round to the nearest tenth of a second.
A $20$ -foot ladder, leaning against a building, reaches a height of $19$ feet. How far is the base of the ladder from the wall? Round to the nearest tenth of a foot.

Answer

1. $\pm 9$

3. $\pm \frac{2 \sqrt{2}}{3}$

5. $\pm \frac{\sqrt{14}}{2}$

7. $-\frac{1}{2}, \frac{7}{2}$

9. $3\pm \frac{2}{3} i$

11. $\pm i \sqrt{5}$

13. $1.1$ seconds

Exercise $\PageIndex{2}$

Solve by completing the square.

$x^{2}+4 x-5=0$
$x^{2}+2 x-17=0$
$x^{2}-4 x+1=0$
$x^{2}-6 x-2=0$
$x^{2}-3 x-1=0$
$x^{2}+5 x-6=0$
$x^{2}+x-2=0$
$x^{2}-x-4=0$
$5 x^{2}-10 x+1=0$
$4 x^{2}+8 x-3=0$
$2 x^{2}-6 x+1=0$
$3 x^{2}+10 x+6=0$
$x^{2}-x+3=0$
$2 x^{2}+6 x+5=0$
$x(x+9)+10=5 x+2$
$(2 x+5)(x+2)=8 x+7$

Answer

1. $-5,1$

3. $2\pm \sqrt{3}$

5. $\frac{3 \pm \sqrt{13}}{2}$

7. $-2,1$

9. $\frac{5 \pm 2 \sqrt{5}}{5}$

11. $\frac{3 \pm \sqrt{7}}{2}$

13. $\frac{1}{2} \pm \frac{\sqrt{11}}{2} i$

15. $-2 \pm 2 i$

Exercise $\PageIndex{3}$

Solve using the quadratic formula.

$2 x^{2}-x-6=0$
$3 x^{2}+x-4=0$
$9 x^{2}+12 x+2=0$
$25 x^{2}-10 x-1=0$
$-x^{2}+8 x-2=0$
$-x^{2}-x+1=0$
$5-2 x-x^{2}=0$
$2+4 x-3 x^{2}=0$
$3 x^{2}-2 x+4=0$
$7 x^{2}-x+1=0$
$-x^{2}+2 x-6=0$
$-3 x^{2}+4 x-2=0$
$36 x^{2}+60 x+25=0$
$72 x^{2}+54 x-35=0$
$1.3 x^{2}-2.8 x-4.2=0$
$5.5 x^{2}-4.1 x+2.2=0$
$(x+2)^{2}-3 x=4$
$(3 x+1)^{2}-6=6 x-3$
The height in feet of a baseball tossed upward at a speed of $48$ feet per second from the ground is given by the function, $h (t) = −16t^{2} + 48t$ , where $t$ represents the time in seconds after the ball is tossed. At what time does the baseball reach a height of $18$ feet? Round off to the nearest hundredth of a second.
The height in feet reached by a model rocket launched from a $3$ -foot platform is given by the function $h(t) = −16t^{2} + 256t + 3$ where $t$ represents time in seconds after launch. At what times will the rocket reach $1,000$ feet? Round off to the nearest tenth of a second.

Answer

1. $-\frac{3}{2}, 2$

3. $\frac{-2 \pm \sqrt{2}}{3}$

5. $4\pm \sqrt{14}$

7. $-1 \pm \sqrt{6}$

9. $\frac{1}{3} \pm \frac{\sqrt{11}}{3} i$

11. $1\pm i \sqrt{5}$

13. $-\frac{5}{6}$

15. $x \approx-1.0, x \approx 3.2$

17. $-1,0$

19. The ball will reach $18$ feet at $0.44$ seconds and again at $2.56$ seconds.

Exercise $\PageIndex{4}$

Use the discriminant to determine the number and type of solutions.

$-x^{2}+6 x+1=0$
$-x^{2}+x-3=0$
$4 x^{2}-4 x+1=0$
$16 x^{2}-9=0$

Answer

1. Two irrational solutions

3. One rational solution

Exercise $\PageIndex{5}$

Solve using any method.

$x^{2}-4 x-96=0$
$25 x^{2}+x=0$
$25 t^{2}-1=0$
$t^{2}+25=0$
$y^{2}-y-7=0$
$5 y^{2}-25 y=0$
$2 x^{2}-9=0$
$25 x^{2}-10 x+1=0$
$(2 x+5)^{2}-9=0$
$(x-2)(x-5)=5$
The length of a rectangle is $3$ inches less than twice the width. If the area of the rectangle measures $30$ square inches, then find the dimensions of the rectangle. Round off to the nearest hundredth of an inch.
The value in dollars of a new car is modeled by the function $V (t) = 125t^{2} − 2,500t + 18,000$ where $t$ represents the number of years since it was purchased. Determine the age of the car when its value is $ $18,000$ .

Answer

1. $-8,12$

3. $\pm \frac{1}{5}$

5. $\frac{1 \pm \sqrt{29}}{2}$

7. $\pm \frac{3 \sqrt{2}}{2}$

9. $-4,-1$

11. Length: $6.38$ inches; width: $4.69$ inches

Exercise $\PageIndex{6}$

Find all solutions.

$x^{4}-16 x^{2}+48=0$
$x^{2 / 3}-x^{1 / 3}-20=0$
$x^{-2}-5 x^{-1}-50=0$
$\left(\frac{t+3}{t}\right)^{2}+11\left(\frac{t+3}{t}\right)-12=0$
$x+2 \sqrt{x}-24=0$
$2 x^{1 / 2}-3 x^{1 / 4}+1=0$
$4\left(\frac{1}{x+1}\right)^{2}-4\left(\frac{1}{x+1}\right)-3=0$
$5 t^{-2}-27 t^{-1}-18=0$
$3 x^{2 / 3}-5 x^{1 / 3}+2=0$
$4 x+4 \sqrt{x}+1=0$
$16 y^{4}-25=0$
$x^{-2}-64=0$

Answer

1. $\pm 2, \pm 2 \sqrt{3}$

3. $-\frac{1}{5}, \frac{1}{10}$

5. $16$

7. $-3,-\frac{1}{3}$

9. $1, \frac{8}{27}$

11. $\pm \frac{\sqrt{5}}{2}, \pm \frac{\sqrt{5}}{2} i$

Exercise $\PageIndex{7}$

Find the set of all roots.

$f(x)=x^{2}-50$
$f(x)=x^{3}-64$
$f(x)=x^{4}-81$
$f(x)=x^{4}+8 x$

Answer

1. $\{\pm 5 \sqrt{2}\}$

3. $\{\pm 3, \pm 3 i\}$

Exercise $\PageIndex{8}$

Find a quadratic equation with integer coefficients and the given set of solutions.

$\left\{\frac{4}{3},-\frac{1}{2}\right\}$
$\{\pm \sqrt{5}\}$
$\{\pm 4 \sqrt{2}\}$
$\{\pm 6 i\}$
$\{2 \pm i\}$
$\{3 \pm \sqrt{5}\}$

Answer

1. $6 x^{2}-5 x-4=0$

3. $x^{2}-32=0$

5. $x^{2}-4 x+5=0$

Exercise $\PageIndex{9}$

Determine the $x$ - and $y$ -intercepts.

$y=2 x^{2}+5 x-12$
$y=x^{2}-18$
$y=x^{2}+4 x+7$
$y=-9 x^{2}+12 x-4$

Answer

1. $x$ -intercepts: $(−4, 0), ( \frac{3}{2} , 0)$ ; $y$ -intercept: $(0, −12)$

3. $x$ -intercepts: none; $y$ -intercept: $(0, 7)$

Exercise $\PageIndex{10}$

Find the vertex and the line of symmetry.

$y=x^{2}-4 x-12$
$y=-x^{2}+8 x-1$
$y=x^{2}+3 x-1$
$y=4 x^{2}-1$

Answer

1. Vertex: $(2, −16)$ ; line of symmetry: $x = 2$

3. Vertex: $(−\frac{3}{2} , −\frac{13}{4} )$ ; line of symmetry: $x = −\frac{3}{2}$

Exercise $\PageIndex{11}$

Graph. Find the vertex and the $y$ -intercept. In addition, find the $x$ -intercepts if they exist.

$y=x^{2}+8 x+12$
$y=-x^{2}-6 x+7$
$y=-2 x^{2}-4$
$y=x^{2}+4 x$
$y=4 x^{2}-4 x+1$
$y=-2 x^{2}$
$y=-2 x^{2}+8 x-7$
$y=3 x^{2}-1$

Answer

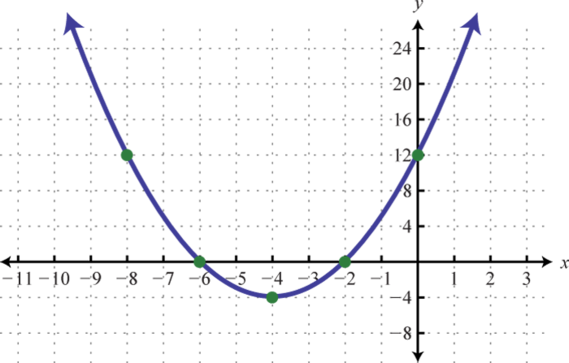
Figure 6.E.1

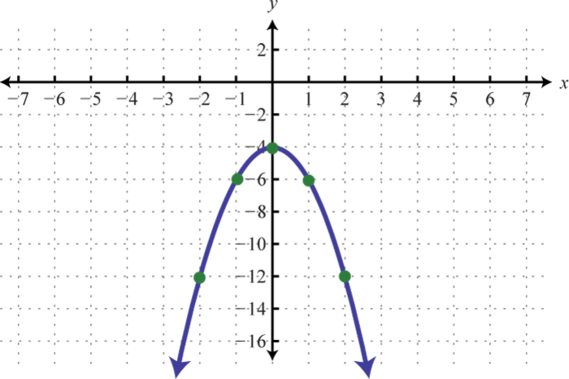
Figure 6.E.2

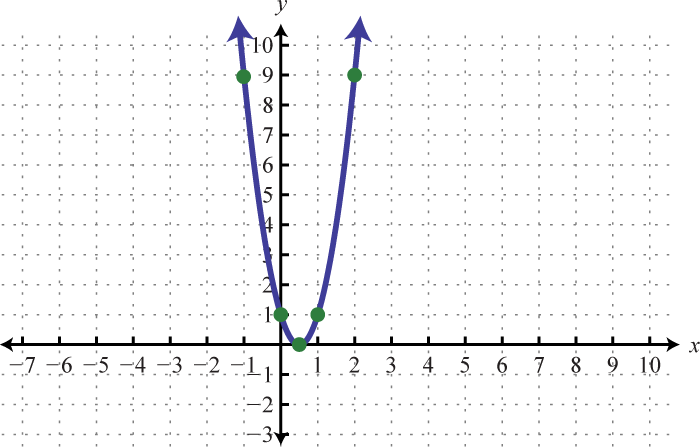
Figure 6.E.3

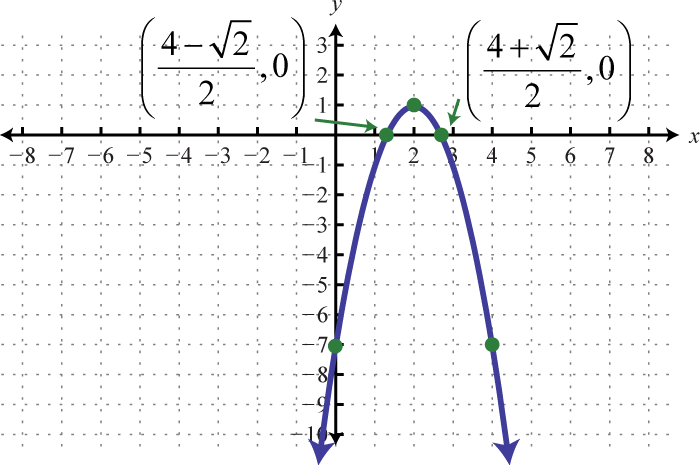
Figure 6.E.4

Exercise $\PageIndex{12}$

Determine the maximum or minimum $y$ -value.

$y=x^{2}-10 x+1$
$y=-x^{2}+10 x-1$
$y=-3 x^{2}+2 x-1$
$y=2 x^{2}-x+2$

Answer

1. Minimum: $y = −24$

3. Maximum: $y = −\frac{2}{3}$

Exercise $\PageIndex{13}$

Rewrite in vertex form $y = a(x − h)^{2} + k$ and determine the vertex.

$y=x^{2}-6 x+13$
$y=x^{2}+10 x+24$
$y=2 x^{2}-4 x-1$
$y=-x^{2}-8 x-11$

Answer

1. $y=(x-3)^{2}+4$ ; vertex: $(3,4)$

3. $y=2(x-1)^{2}-3$ ; vertex: $(1,-3)$

Exercise $\PageIndex{14}$

Graph. Find the vertex and the $y$ -intercept. In addition, find the $x$ -intercepts if they exist.

$f(x)=(x-4)^{2}-2$
$f(x)=-(x+6)^{2}+4$
$f(x)=-x^{2}+10$
$f(x)=(x+10)^{2}-20$
$f(x)=2(x-1)^{2}-3$
$f(x)=-3(x+1)^{2}-2$
The value in dollars of a new car is modeled by $V (t) = 125t^{2} − 3,000t + 22,000$ where $t$ represents the number of years since it was purchased. Determine the age of the car when its value is at a minimum.
The height in feet of a baseball tossed upward at a speed of $48$ feet per second from the ground is given by the function, $h (t) = −16t^{2} + 32t$ , where $t$ represents the time in seconds after it is tossed. What is the maximum height of the baseball?
The rectangular area in square feet that can be enclosed with $200$ feet of fencing is given by $A (w) = w (100 − w)$ where $w$ represents the width of the rectangular area in feet. What dimensions will maximize the area that can be enclosed?
A manufacturing company has found that production costs in thousands of dollars are modeled by $C (x) = 0.4x^{2} − 72x + 8,050$ where $x$ represents the number of employees. Determine the number of employees that will minimize production costs.

Answer

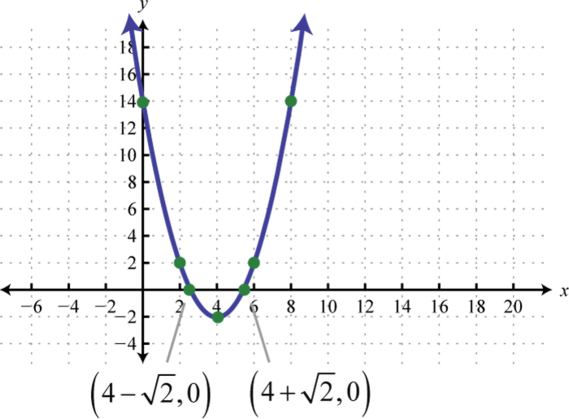
Figure 6.E.5

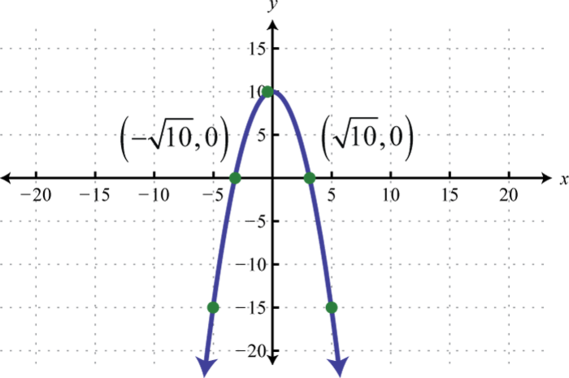
Figure 6.E.6

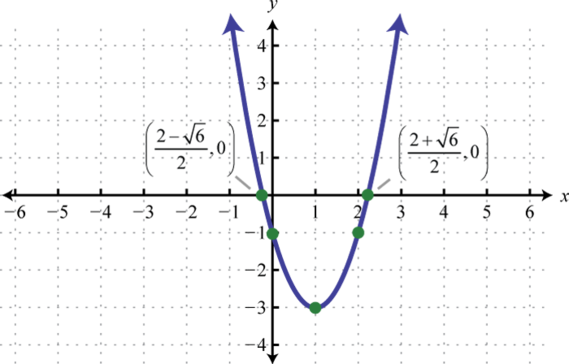
Figure 6.E.7

7. The car will have minimum value $12$ years after it is purchased.

9. Length: $50$ feet; width: $50$ feet

Exercise $\PageIndex{15}$

Solve. Present answers using interval notation.

$-2(x-1)(x+3)<0$
$x^{2}+2 x-35<0$
$x^{2}-6 x-16 \leq 0$
$x^{2}+14 x+40 \geq 0$
$x^{2}-10 x-24>0$
$36-x^{2}>0$
$1-9 x^{2}<0$
$8 x-12 x^{2} \leq 0$
$5 x^{2}+3 \leq 0$
$x^{2}-28 \geq 0$
$9 x^{2}-30 x+25 \leq 0$
$x^{2}-8 x+18>0$
$x^{2}-2 x-4<0$
$-x^{2}+3 x+18>0$

Answer

1. $(-\infty,-3) \cup(1, \infty)$

3. $[-2,8]$

5. $(-\infty,-2) \cup(12, \infty)$

7. $\left(-\infty,-\frac{1}{3}\right) \cup\left(\frac{1}{3}, \infty\right)$

9. $\varnothing$

11. $\frac{5}{3}$

13. $(1-\sqrt{5}, 1+\sqrt{5})$

Exercise $\PageIndex{16}$

Find the domain of the function.

$f(x)=\sqrt{x^{2}-100}$
$f(x)=\sqrt{3 x-6 x^{2}}$
$g(x)=\sqrt{3 x^{2}+9}$
$g(x)=\sqrt{8+2 x-x^{2}}$

Answer

1. $(-\infty,-10] \cup[10, \infty)$

3. $(-\infty, \infty)$

Exercise $\PageIndex{17}$

Solve. Present answers using interval notation.

$x(x-5)(x+2)>0$
$(x+4)^{2}(x-3)<0$
$x^{2}(x+3) \geq 0$
$x(x-1)^{2} \leq 0$
$x^{3}+4 x^{2}-9 x-36>0$
$2 x(4 x-1) \geq 3$
$4 x^{3}-12 x^{2}+9 x<0$
$x^{3}-9 x^{2}+20 x \geq 0$
$x^{3}-2 x^{2}-x+2<0$
$6 x(x+1)+5 x \leq 35$
$\frac{(x-2)(2 x+1)}{x(x-1)} \leq 0$
$\frac{x(x-3)^{2}}{x-4} \leq 0$
$\frac{x^{2}+4 x+4}{4 x^{2}-1}<0$
$\frac{x^{2}-10 x+24}{x^{2}+10 x+25}>0$
$\frac{1}{x-2}+\frac{3}{x} \geq 0$
$\frac{2}{x-1}-\frac{1}{x+1} \leq 0$
$\frac{3(x+1)}{x^{2}+2 x-3} \leq \frac{2}{x-1}$
$\frac{x-4}{x+5} \geq \frac{x-2}{x-5}$

Answer

1. $(-2,0) \cup(5, \infty)$

3. $[-3, \infty)$

5. $(-4,-3) \cup(3, \infty)$

7. $(-\infty, 0)$

9. $(-\infty,-1) \cup(1,2)$

11. $\left[-\frac{1}{2}, 0\right) \cup(1,2]$

13. $\left(-\frac{1}{2}, \frac{1}{2}\right)$

15. $\left(0, \frac{3}{2}\right] \cup(2, \infty)$

17. $(-\infty,-3) \cup(1,3]$

Sample Exam

Exercise $\PageIndex{18}$

Solve by extracting the roots: $2 x^{2}-5=0$ .
Solve by completing the square: $x^{2}-16 x+1=0$ .

Answer: 1. $\pm \frac{\sqrt{10}}{2}$

Exercise $\PageIndex{19}$

Solve using the quadratic formula.

$x^{2}+x+1=0$
$2 x^{2}-x-4=0$
$-4 x^{2}+2 x-1=0$
$(x-4)(x-2)=6$

Answer

1. $-\frac{1}{2} \pm \frac{\sqrt{3}}{2} i$

3. $\frac{1}{4} \pm \frac{\sqrt{3}}{4} i$

Exercise $\PageIndex{20}$

Find a quadratic equation with integer coefficients and solutions $\{\pm \sqrt{5}\}$ .
The area of a rectangle is $22$ square centimeters. If the length is $5$ centimeters less than twice the width, then find the dimensions of the rectangle. Round off to the nearest tenth of a centimeter.
Assuming dry road conditions and average reaction times, the safe stopping distance in feet of a certain car is given by $d(x)=\frac{1}{20} x^{2}+x$ where $x$ represents the speed of the car in miles per hour. Determine the safe speed of the car if you expect to stop in $100$ feet. Round off to the nearest mile per hour.

Answer

1. $x^{2}-5=0$

9. $36$ miles per hour

Exercise $\PageIndex{21}$

Find all solutions.

$x^{4}+x^{2}-12=0$
$3 x^{-2}-5 x^{-1}-2=0$
$2 x^{2 / 3}+3 x^{1 / 3}-2=0$
$x-3 \sqrt{x}-4=0$
$\left(\frac{t}{t+1}\right)^{2}+4\left(\frac{t}{t+1}\right)-12=0$

Answer

2. $-3, \frac{1}{2}$

4. $16$

Exercise $\PageIndex{22}$

Graph. Find the vertex and the $y$ -intercept. In addition, find the $x$ -intercepts if they exist.

$f(x)=x^{2}+4 x-12$
$f(x)=-x^{2}+2 x+3$

Answer

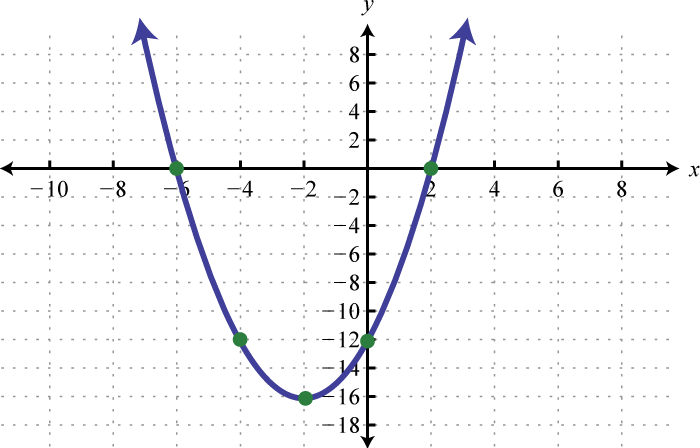
Figure 6.E.8

Exercise $\PageIndex{23}$

Given the function defined by y=3x2−6x−5:
1. Does the function have a minimum or maximum? Explain.
2. Find the minimum or maximum $y$ -value.
The height in feet of a water rocket launched from the ground is given by the function $h (t) = −16t^{2} + 96t$ where $t$ represents the number of seconds after launch. What is the maximum height attained by the rocket?

Answer: 1. (1) Minimum (2) $y=-8$

Exercise $\PageIndex{24}$

Sketch the graph and use it to solve the given inequality.

Graph $f(x)=(x+1)^{2}-4$ and find $x$ where $f(x) \geq 0$ .
Graph $f(x)=-x^{2}+4$ and find $x$ where $f(x) \geq 0$ .

Answer

1. $(-\infty,-3] \cup[1, \infty)$

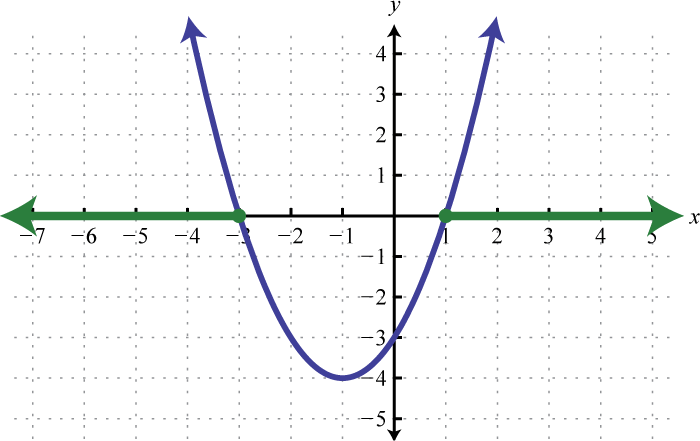
Figure 6.E.9

Exercise $\PageIndex{25}$

Solve. Present answers using interval notation.

$x^{2}-2 x-15<0$
$x(2 x-1)>10$
$x(x+3)(x-2)^{2} \leq 0$
$\frac{x^{2}-10 x+25}{x+1} \geq 0$
$\frac{x^{2}-5 x+4}{x^{2}+x} \leq 0$

Answer

1. $(-3,5)$

3. $[-3,0] \cup\{2\}$

5. $(-1,0) \cup[1,4]$

Sample Exam

Support Center

How can we help?