8.2: Circles
- Page ID
- 6283
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Learning Objectives
- Graph a circle in standard form.
- Determine the equation of a circle given its graph.
- Rewrite the equation of a circle in standard form.
The Circle in Standard Form
A circle8 is the set of points in a plane that lie a fixed distance, called the radius9, from any point, called the center. The diameter10 is the length of a line segment passing through the center whose endpoints are on the circle. In addition, a circle can be formed by the intersection of a cone and a plane that is perpendicular to the axis of the cone:
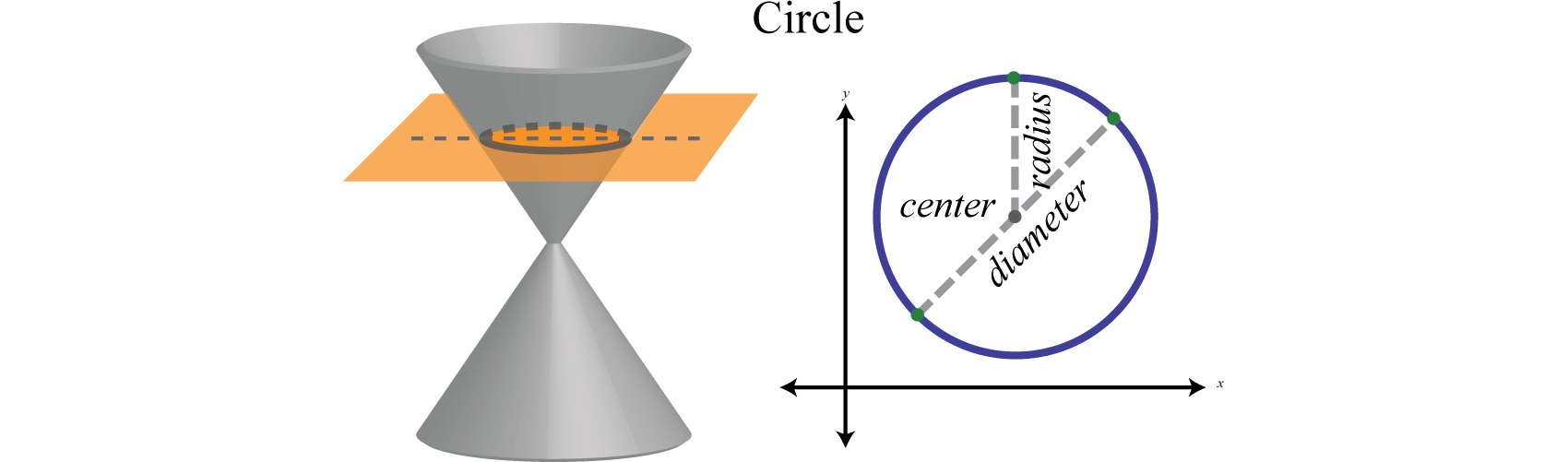
In a rectangular coordinate plane, where the center of a circle with radius \(r\) is \((h,k)\), we have

Calculate the distance between \((h,k)\) and \((x,y)\) using the distance formula,
\(\sqrt{(x-h)^{2}+(y-k)^{2}}=r\)
Squaring both sides leads us to the equation of a circle in standard form11,
\((x-h)^{2}+(y-k)^{2}=r^{2}\)
In this form, the center and radius are apparent. For example, given the equation \((x-2)^{2}+(y+5)^{2}=16\) we have,
\(\begin{array}{l}{(x-h)^{2}\:+\:(x\:-k)^{2}=r^{2}} \\ \quad\quad\color{Cerulean}{\downarrow}\quad\quad\quad\quad\:\color{Cerulean}{\downarrow}\quad\quad\color{Cerulean}{\downarrow} \\ {(x-\color{Cerulean}{2}\color{black}{)}^{2}+[y-(\color{Cerulean}{-5}\color{black}{)}]^{2}=\color{Cerulean}{4}^{\color{black}{2}}}\end{array}\)
In this case, the center is \((2,−5)\) and \(r=4\). More examples follow:
| Equation | Center | Radius |
|---|---|---|
| \((x-3)^{2}+(y-4)^{2}=25\) | \((3,4)\) | \(r=5\) |
| \((x-1)^{2}+(y+2)^{2}=7\) | \((1,-2)\) | \(r=\sqrt{7}\) |
| \((x+4)^{2}+(y-3)^{2}=1\) | \((-4,3)\) | \(r=1\) |
| \(x^{2}+(y+6)^{2}=8\) | \((0,-6)\) | \(r=2 \sqrt{2}\) |
The graph of a circle is completely determined by its center and radius.
Example \(\PageIndex{1}\):
Graph: \((x-2)^{2}+(y+5)^{2}=16\).
Solution
Written in this form we can see that the center is \((2,−5)\) and that the radius \(r=4\) units. From the center mark points \(4\) units up and down as well as \(4\) units left and right.
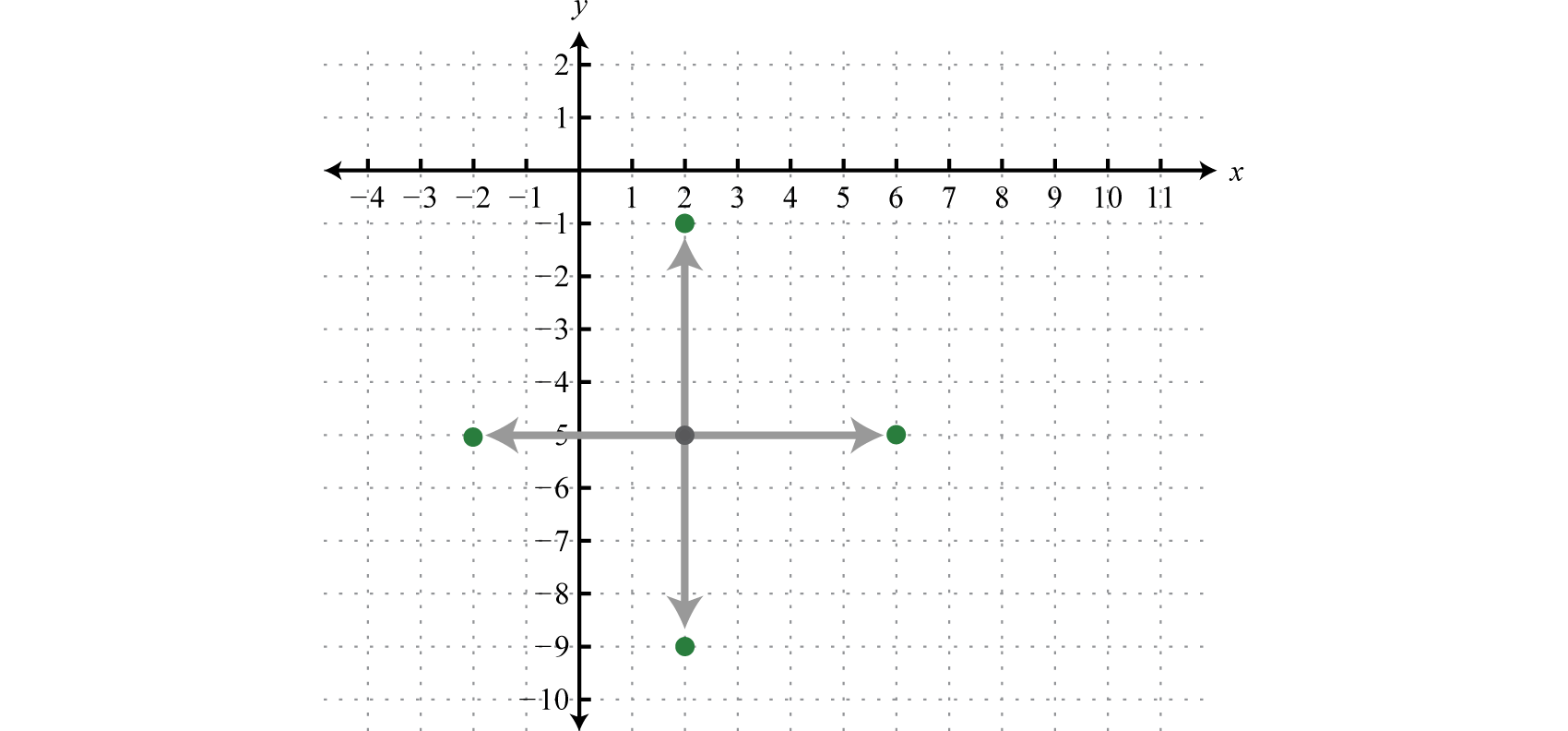
Then draw in the circle through these four points.
Answer:
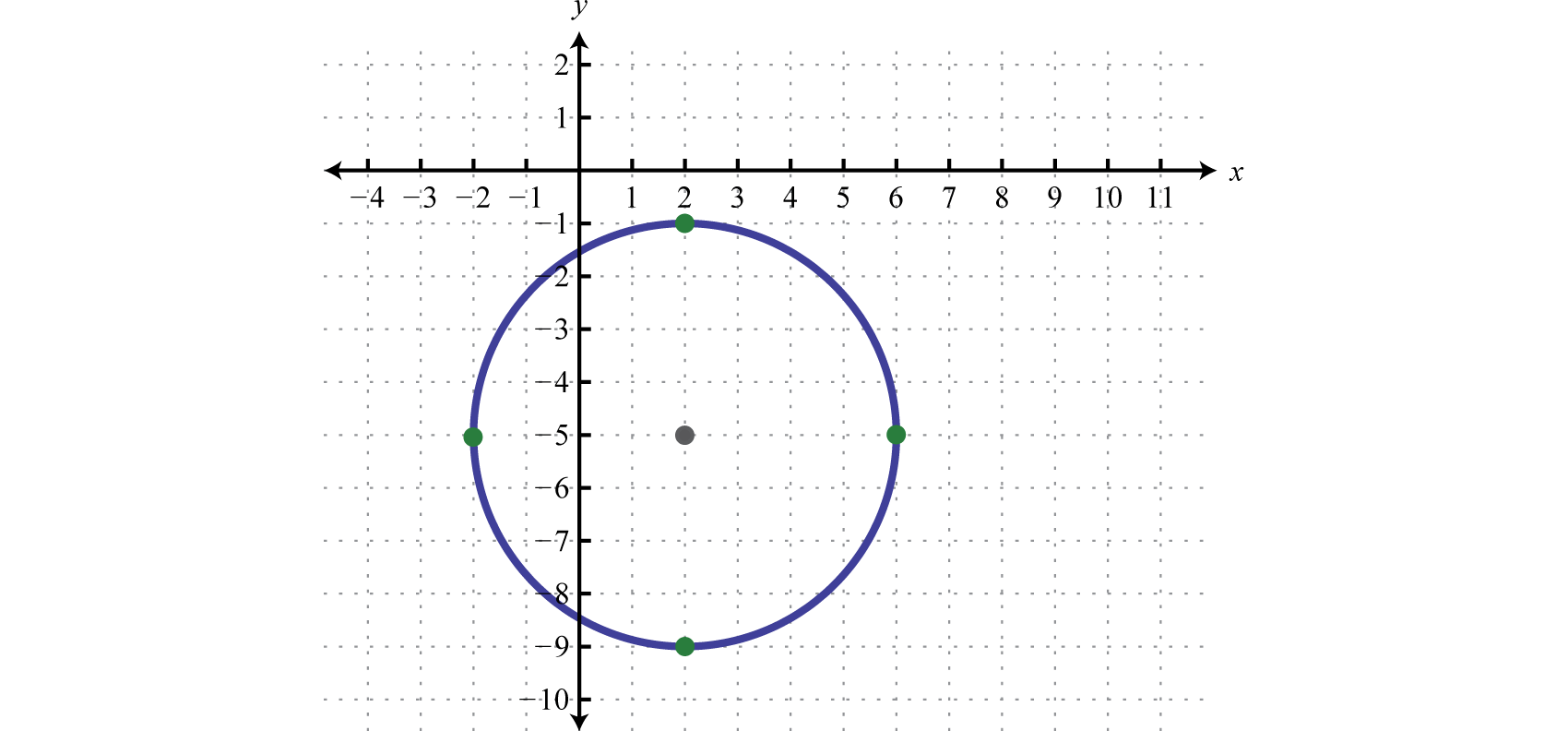
As with any graph, we are interested in finding the \(x\)- and \(y\)-intercepts.
Example \(\PageIndex{2}\):
Find the intercepts: \((x-2)^{2}+(y+5)^{2}=16\).
Solution
To find the \(y\)-intercepts set \(x=0\):
\(\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(\color{Cerulean}{0}\color{black}{-}2)^{2}+(y+5)^{2} &=16 \\ 4+(y+5)^{2} &=16 \end{aligned}\)
For this equation, we can solve by extracting square roots.
\(\begin{aligned}(y+5)^{2} &=12 \\ y+5 &=\pm \sqrt{12} \\ y+5 &=\pm 2 \sqrt{3} \\ y &=-5 \pm 2 \sqrt{3} \end{aligned}\)
Therefore, the \(y\)-intercepts are \((0,-5-2 \sqrt{3})\) and \((0,-5+2 \sqrt{3})\). To find the \(x\)-intercepts set \(y=0\):
\(\begin{aligned}(x-2)^{2}+(y+5)^{2} &=16 \\(x-2)^{2}+(\color{Cerulean}{0}\color{black}{+}5)^{2} &=16 \\(x-2)^{2}+25 &=16 \\(x-2)^{2} &=-9 \\ x-2 &=\pm \sqrt{-9} \\ x &=2 \pm 3 i \end{aligned}\)
And because the solutions are complex we conclude that there are no real \(x\)-intercepts. Note that this does make sense given the graph.
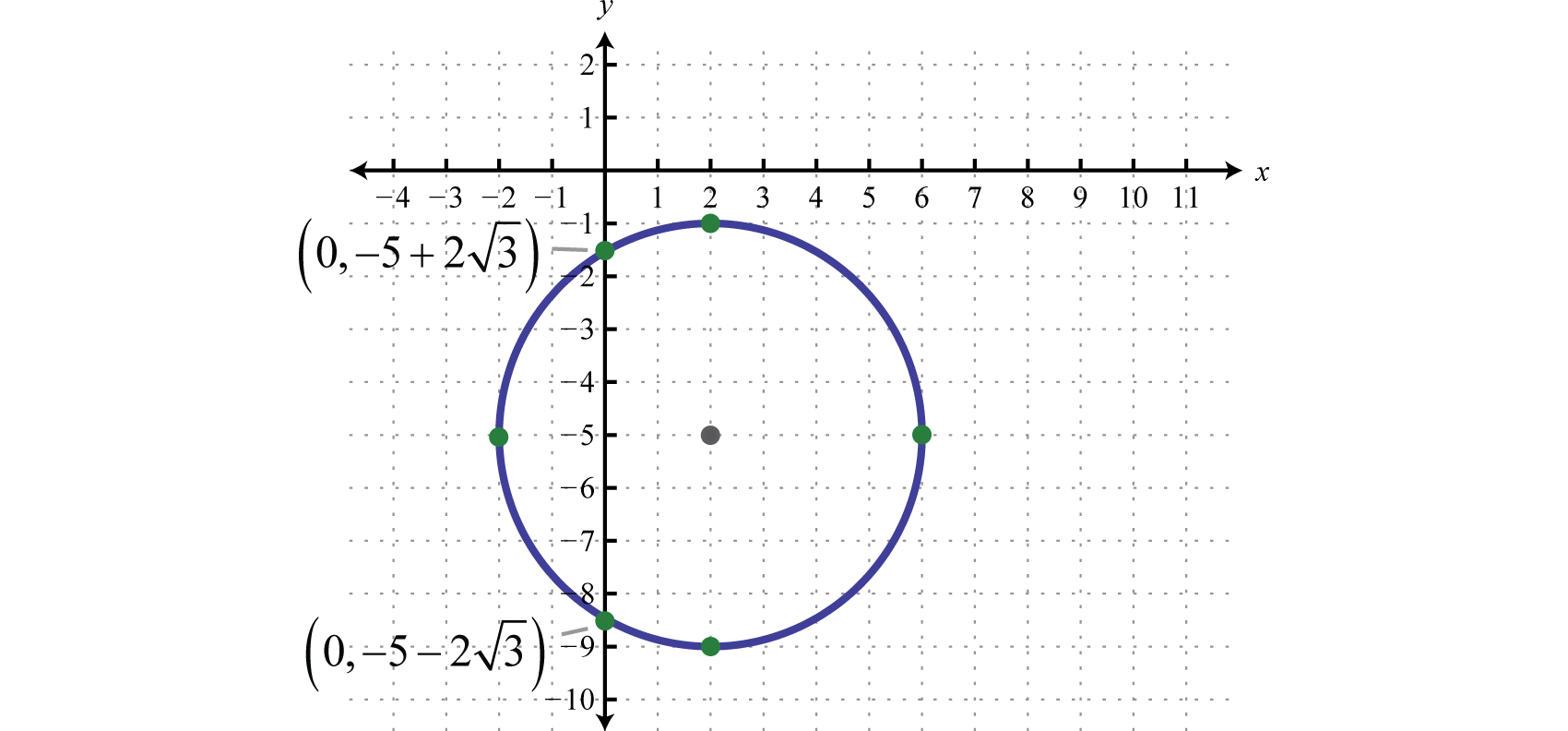
Answer:
\(x\)-intercepts: none; \(y\)-intercepts: \((0,-5-2 \sqrt{3})\) and \((0,-5+2 \sqrt{3})\)
Given the center and radius of a circle, we can find its equation.
Example \(\PageIndex{3}\):
Graph the circle with radius \(r=3\) units centered at \((−1,0)\). Give its equation in standard form and determine the intercepts.
Solution:
Given that the center is \((−1,0)\) and the radius is \(r=3\) we sketch the graph as follows:
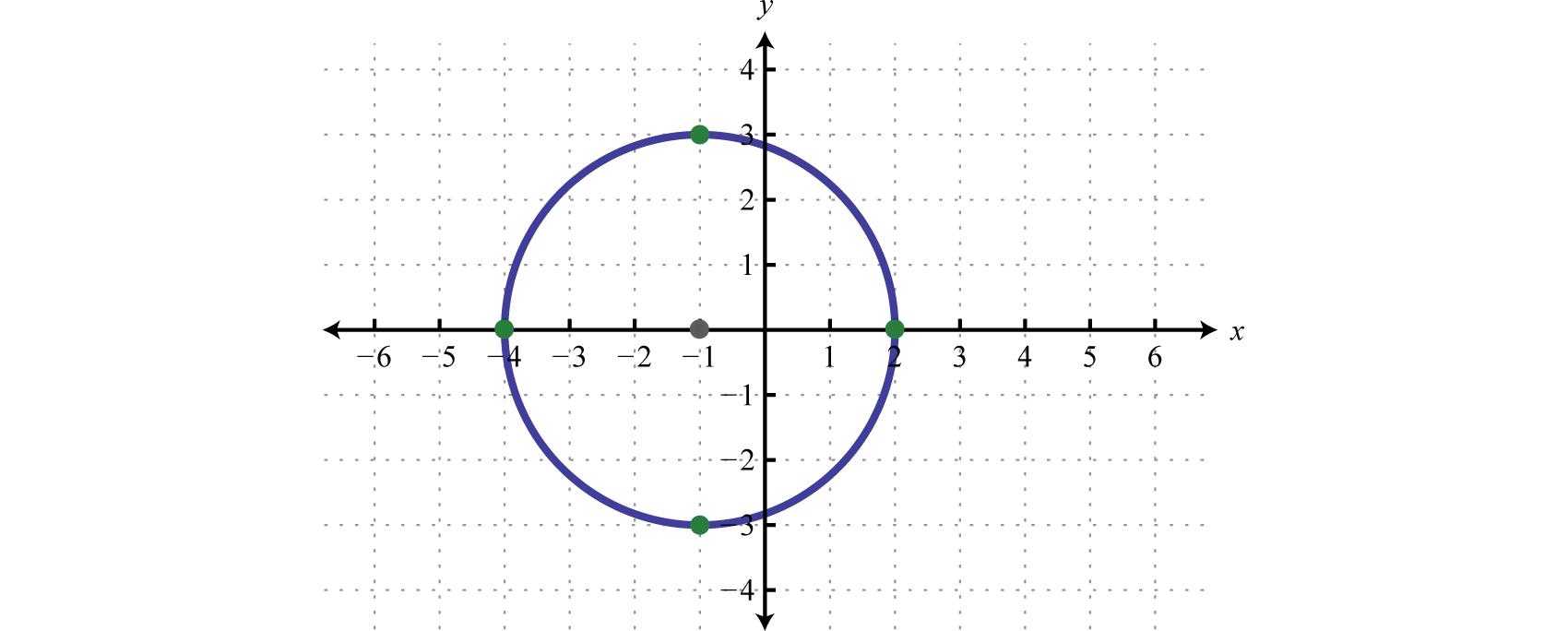
Substitute \(h, k\), and \(r\) to find the equation in standard form. Since \((h,k)=(−1,0)\) and \(r=3\) we have,
\(\begin{aligned} (x-h)^{2}+(y-k)^{2}&=r^{2}\\ [x-(\color{Cerulean}{-1}\color{black}{)}]^{2}+(y-\color{Cerulean}{0}\color{black}{)}^{2}&=\color{Cerulean}{3}\color{black}{^{2}} \\ (x+1)^{2}+y^{2}&=9 \end{aligned}\)
The equation of the circle is \((x+1)^{2}+y^{2}=9\), use this to determine the \(y\)-intercepts.
\(\begin{aligned}(x+1)^{2}+y^{2} &=9 \quad \color{Cerulean} { Set\:x=0\: to\: and\: solve\: for\: y. } \\(\color{Cerulean}{0}\color{black}{+}1)^{2}+y^{2} &=9 \\ 1+y^{2} &=9 \\ y^{2} &=8 \\ y &=\pm \sqrt{8} \\ y &=\pm 2 \sqrt{2} \end{aligned}\)
Therefore, the y-intercepts are \((0,-2 \sqrt{2})\) and \((0,2 \sqrt{2})\). To find the \(x\)-intercepts algebraically, set \(y=0\) and solve for \(x\); this is left for the reader as an exercise.
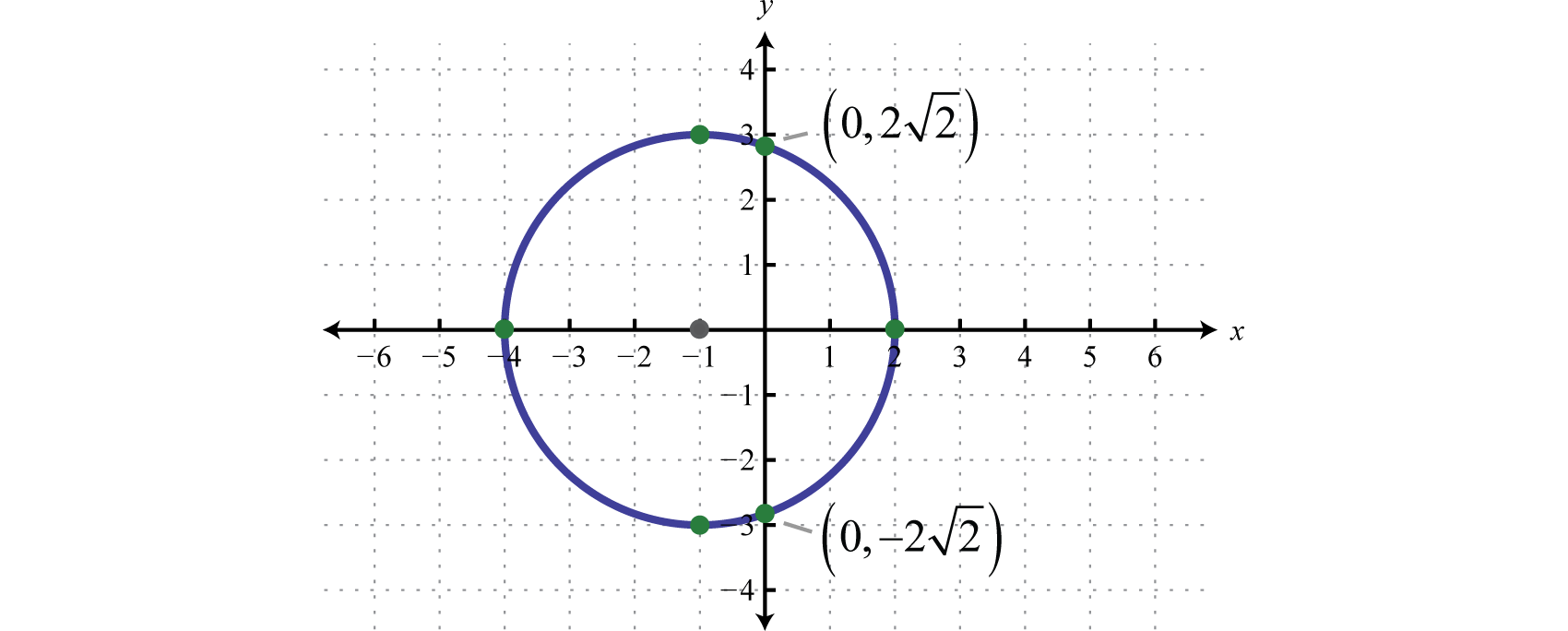
Answer:
Equation: \((x+1)^{2}+y^{2}=9\); \(y\)-intercepts: \((0,-2 \sqrt{2})\) and \((0,2 \sqrt{2})\); \(x\)-intercepts: \((−4,0)\) and \((2,0)\)
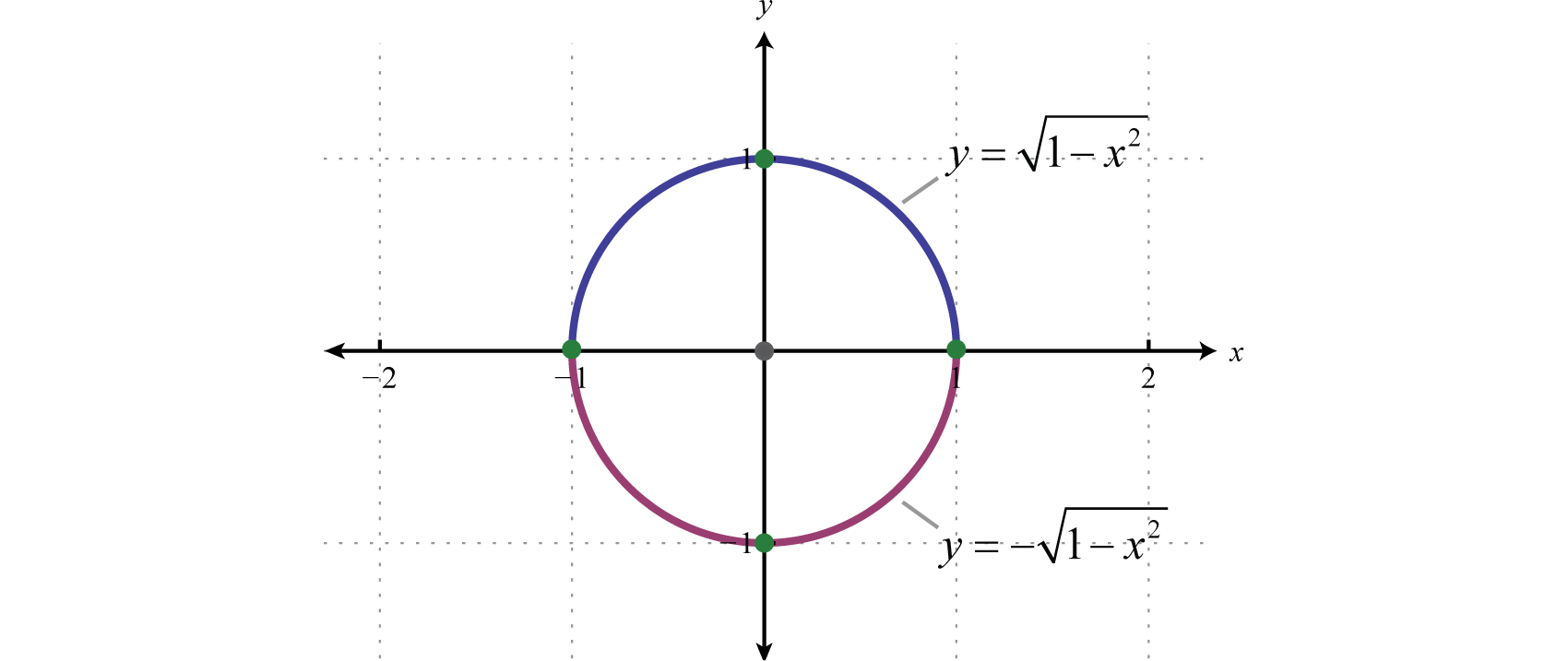
Of particular importance is the unit circle12,
\(x^{2}+y^{2}=1\)
Or,
\((x-0)^{2}+(y-0)^{2}=1^{2}\)
In this form, it should be clear that the center is \((0,0)\) and that the radius is \(1\) unit. Furthermore, if we solve for \(y\) we obtain two functions:
\(\begin{aligned} x^{2}+y^{2} &=1 \\ y^{2} &=1-x^{2} \\ y &=\pm \sqrt{1-x^{2}} \end{aligned}\)
The function defined by \(y=\sqrt{1-x^{2}}\) is the top half of the circle and the function defined by \(y=-\sqrt{1-x^{2}}\) is the bottom half of the unit circle:
Exercise \(\PageIndex{1}\):
Graph and label the intercepts: \(x^{2}+(y+2)^{2}=25\).
Answer:
www.youtube.com/v/KeKt9k6IDCk
The Circle in General Form
We have seen that the graph of a circle is completely determined by the center and radius which can be read from its equation in standard form. However, the equation is not always given in standard form. The equation of a circle in general form13 follows:
\(x^{2}+y^{2}+c x+d y+e=0\)
Here \(c, d\), and \(e\) are real numbers. The steps for graphing a circle given its equation in general form follow.
Example \(\PageIndex{4}\):
Graph: \(x^{2}+y^{2}+6 x-8 y+13=0\).
Solution
Begin by rewriting the equation in standard form.
Step 1: Group the terms with the same variables and move the constant to the right side. In this case, subtract \(13\) on both sides and group the terms involving \(x\) and the terms involving \(y\) as follows.
\(\begin{aligned} x^{2}+y^{2}+6 x-8 y+13 &=0 \\ \left(x^{2}+6 x+\_\_\_\right)+\left(y^{2}-8 y+\_\_\_\right)&=-13 \end{aligned}\)
Step 2: Complete the square for each grouping. The idea is to add the value that completes the square, \(\left(\frac{b}{2}\right)^{2}\), to both sides for both groupings, and then factor. For the terms involving \(x\) use \(\left(\frac{6}{2}\right)^{2}=3^{2}=9\) and for the terms involving \(y\) use \(\left(\frac{-8}{2}\right)^{2}=(-4)^{2}=16\).
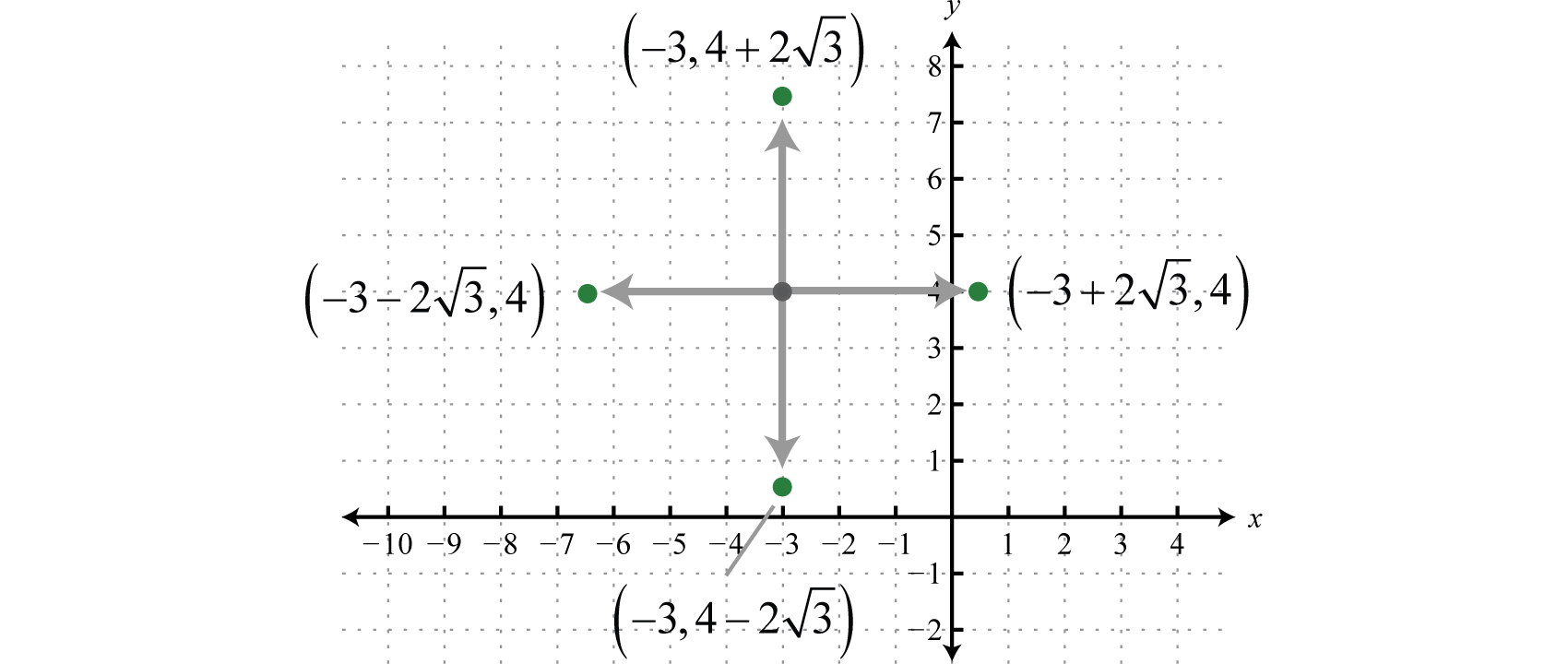
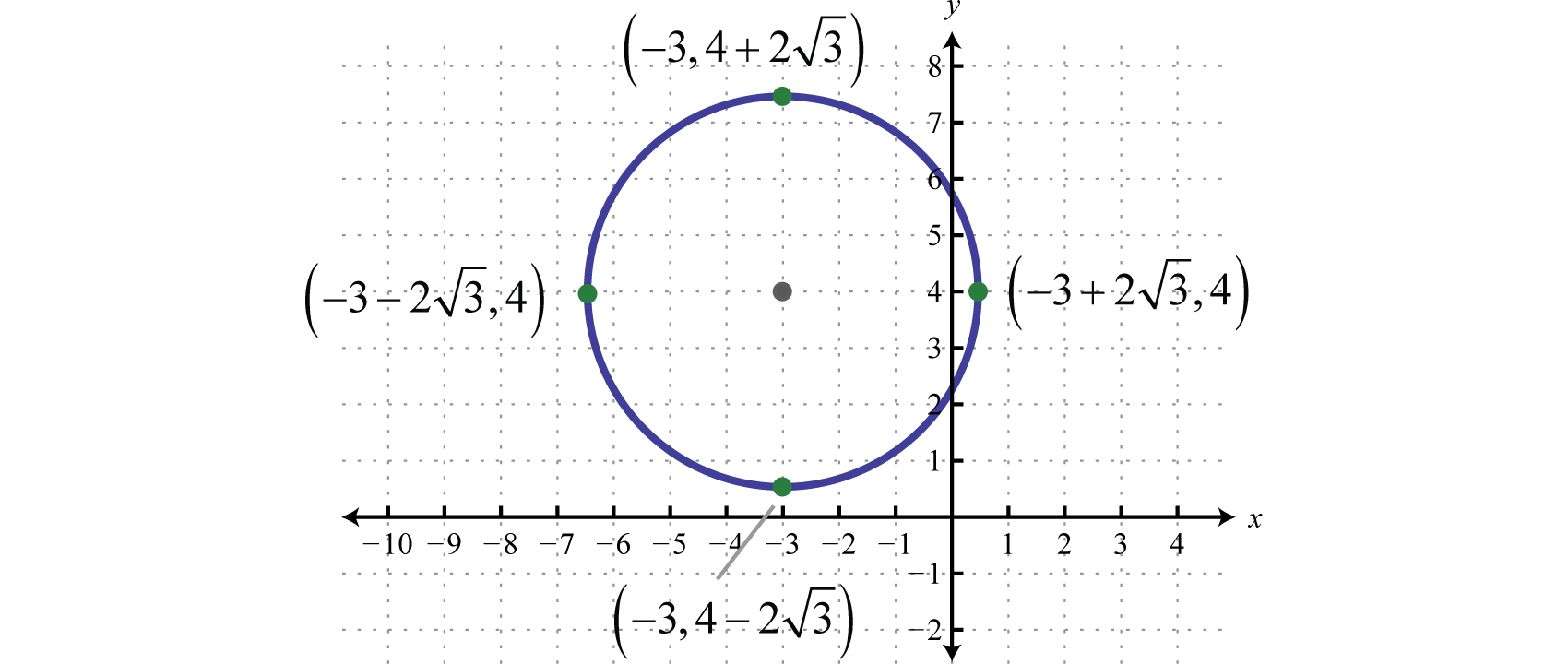
\(\begin{array}{c}{\color{black}{\left(x^{2}+6 x\color{Cerulean}{+9}\right)+}\color{black}{\left(y^{2}-8 y\color{OliveGreen}{+16}\right)=}-13\color{Cerulean}{+9}\color{OliveGreen}{+16}} \\ {(x+3)^{2}+(y-4)^{2}=12}\end{array}\)
Step 3: Determine the center and radius from the equation in standard form. In this case, the center is \((−3,4)\) and the radius \(r=\sqrt{12}=2 \sqrt{3}\).
Step 4: From the center, mark the radius vertically and horizontally and then sketch the circle through these points.
Answer:
Example \(\PageIndex{5}\):
Determine the center and radius: \(4 x^{2}+4 y^{2}-8 x+12 y-3=0\).
Solution
We can obtain the general form by first dividing both sides by \(4\).
\(\frac{4 x^{2}+4 y^{2}-8 x+12 y-3}{4}=\frac{0}{4}\)
\(x^{2}+y^{2}-2 x+3 y-\frac{3}{4}=0\)
Now that we have the general form for a circle, where both terms of degree two have a leading coefficient of \(1\), we can use the steps for rewriting it in standard form. Begin by adding \(\frac{3}{4}\) to both sides and group variables that are the same.
\(\left(x^{2}-2 x+\_\_\_\right)+\left(y^{2}+3 y+\_\_\_\right)=\frac{3}{4}\)
Next complete the square for both groupings. Use \(\left(\frac{-2}{2}\right)^{2}=(-1)^{2}=1\) for the first grouping and \(\left(\frac{3}{2}\right)^{2}=\frac{9}{4}\) for the second grouping.
\(\begin{aligned}\color{black}{\left(x^{2}-2 x\color{Cerulean}{+1}\right)+}\color{black}{\left(y^{2}+3 y\color{OliveGreen}{+\frac{9}{4}}\right)}&=\frac{3}{4}\color{Cerulean}{+1}\color{OliveGreen}{+\frac{9}{4}} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2} &=\frac{16}{4} \\ (x-1)^{2}+\left(y+\frac{3}{2}\right)^{2}&=4\end{aligned}\)
Answer:
Center: \(\left(1,-\frac{3}{2}\right)\); radius: \(r=2\)
In summary, to convert from standard form to general form we multiply, and to convert from general form to standard form we complete the square.

Exercise \(\PageIndex{2}\):
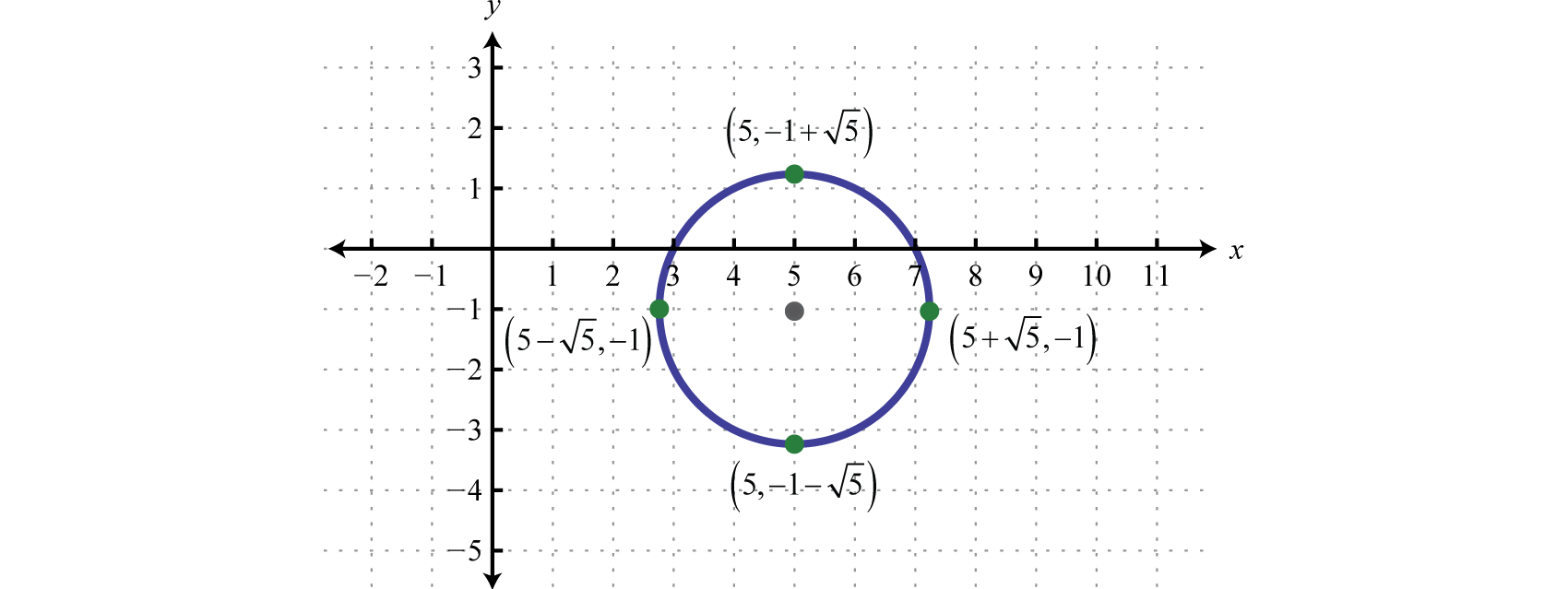
Graph: \(x^{2}+y^{2}-10 x+2 y+21=0\).
Answer:
www.youtube.com/v/Ms8NESnqs6s
Key Takeaways
- The graph of a circle is completely determined by its center and radius.
- Standard form for the equation of a circle is \((x-h)^{2}+(y-k)^{2}=r^{2}\). The center is \((h,k)\) and the radius measures \(r\) units.
- To graph a circle mark points \(r\) units up, down, left, and right from the center. Draw a circle through these four points.
- If the equation of a circle is given in general form \(x^{2}+y^{2}+c x+d y+e=0\), group the terms with the same variables, and complete the square for both groupings. This will result in standard form, from which we can read the circle’s center and radius.
- We recognize the equation of a circle if it is quadratic in both \(x\) and \(y\) where the coefficient of the squared terms are the same.
Exercise \(\PageIndex{3}\)
Determine the center and radius given the equation of a circle in standard form.
- \((x-5)^{2}+(y+4)^{2}=64\)
- \((x+9)^{2}+(y-7)^{2}=121\)
- \(x^{2}+(y+6)^{2}=4\)
- \((x-1)^{2}+y^{2}=1\)
- \((x+1)^{2}+(y+1)^{2}=7\)
- \((x+2)^{2}+(y-7)^{2}=8\)
- Answer
-
1. Center: \((5, −4)\); radius: \(r = 8\)
3. Center: \((0, −6)\); radius: \(r = 2\)
5. Center: \((−1, −1)\); radius: \(r = \sqrt{7}\)
Exercise \(\PageIndex{4}\)
Determine the standard form for the equation of the circle given its center and radius.
- Center \((5, 7)\) with radius \(r = 7\).
- Center \((−2, 8)\) with radius \(r = 5\).
- Center \((6, −11)\) with radius \(r = \sqrt{2}\).
- Center \((−4, −5)\) with radius \(r = \sqrt{6}\).
- Center \((0, −1)\) with radius \(r = 2\sqrt{5}\).
- Center \((0, 0)\) with radius \(r = 3\sqrt{10}\).
- Answer
-
1. \((x-5)^{2}+(y-7)^{2}=49\)
3. \((x-6)^{2}+(y+11)^{2}=2\)
5. \(x^{2}+(y+1)^{2}=20\)
Exercise \(\PageIndex{5}\)
Graph.
- \((x-1)^{2}+(y-2)^{2}=9\)
- \((x+3)^{2}+(y-3)^{2}=25\)
- \((x-2)^{2}+(y+6)^{2}=4\)
- \((x+6)^{2}+(y+4)^{2}=36\)
- \(x^{2}+(y-4)^{2}=1\)
- \((x-3)^{2}+y^{2}=4\)
- \(x^{2}+y^{2}=12\)
- \(x^{2}+y^{2}=8\)
- \((x-7)^{2}+(y-6)^{2}=2\)
- \((x+2)^{2}+(y-5)^{2}=5\)
- \((x+3)^{2}+(y-1)^{2}=18\)
- \((x-3)^{2}+(y-2)^{2}=15\)
- Answer
-
1.
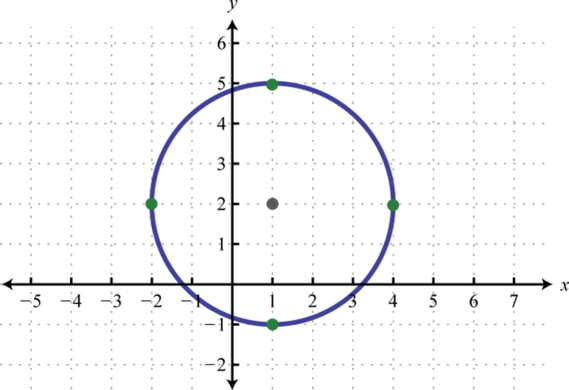
Figure \(\PageIndex{14}\) 3.

Figure \(\PageIndex{15}\) 5.

Figure \(\PageIndex{16}\) 7.

Figure \(\PageIndex{17}\) 9.

Figure \(\PageIndex{18}\) 11.

Figure \(\PageIndex{19}\)
Exercise \(\PageIndex{6}\)
Find the \(x\)- and \(y\)-intercepts.
- \((x-1)^{2}+(y-2)^{2}=9\)
- \((x+5)^{2}+(y-3)^{2}=25\)
- \(x^{2}+(y-4)^{2}=1\)
- \((x-3)^{2}+y^{2}=18\)
- \(x^{2}+y^{2}=50\)
- \(x^{2}+(y+9)^{2}=20\)
- \((x-4)^{2}+(y+5)^{2}=10\)
- \((x+10)^{2}+(y-20)^{2}=400\)
- Answer
-
1. \(x\)-intercepts: \((1 \pm \sqrt{5}, 0)\); \(y\)-intercepts: \((0,2 \pm 2 \sqrt{2})\)
3. \(x\)-intercepts: none; \(y\)-intercepts: \((0, 3), (0, 5)\)
5. \(x\)-intercepts: \((\pm 5 \sqrt{2}, 0)\); \(y\)-intercepts: \((0, \pm 5 \sqrt{2})\)
7. \(x\)-intercepts: none; \(y\)-intercepts: none
Exercise \(\PageIndex{7}\)
Find the equation of the circle.
- Circle with center \((1, −2)\) passing through \((3, −4)\).
- Circle with center \((−4, −1)\) passing through \((0, −3)\).
- Circle whose diameter is defined by \((5, 1)\) and \((−1, 7)\).
- Circle whose diameter is defined by \((−5, 7)\) and \((−1, −5)\).
- Circle with center \((5, −2)\) and area \(9π\) square units.
- Circle with center \((−8, −3)\) and circumference \(12π\) square units.
- Find the area of the circle with equation \((x+12)^{2} \pm(x-5)^{2}=7\).
- Find the circumference of the circle with equation \((x+1)^{2}+(y+5)^{2}=8\).
- Answer
-
1. \((x-1)^{2}+(y+2)^{2}=8\)
3. \((x-2)^{2}+(y-4)^{2}=18\)
5. \((x-5)^{2}+(y+2)^{2}=9\)
7. \(7π\) square units
Exercise \(\PageIndex{8}\)
Rewrite in standard form and graph.
- \(x^{2}+y^{2}+4 x-2 y-4=0\)
- \(x^{2}+y^{2}-10 x+2 y+10=0\)
- \(x^{2}+y^{2}+2 x+12 y+36=0\)
- \(x^{2}+y^{2}-14 x-8 y+40=0\)
- \(x^{2}+y^{2}+6 y+5=0\)
- \(x^{2}+y^{2}-12 x+20=0\)
- \(x^{2}+y^{2}+8 x+12 y+16=0\)
- \(x^{2}+y^{2}-20 x-18 y+172=0\)
- \(4 x^{2}+4 y^{2}-4 x+8 y+1=0\)
- \(9 x^{2}+9 y^{2}+18 x+6 y+1=0\)
- \(x^{2}+y^{2}+4 x+8 y+14=0\)
- \(x^{2}+y^{2}-2 x-4 y-15=0\)
- \(x^{2}+y^{2}-x-2 y+1=0\)
- \(x^{2}+y^{2}-x+y-\frac{1}{2}=0\)
- \(4 x^{2}+4 y^{2}+8 x-12 y+5=0\)
- \(9 x^{2}+9 y^{2}+12 x-36 y+4=0\)
- \(2 x^{2}+2 y^{2}+6 x+10 y+9=0\)
- \(9 x^{2}+9 y^{2}-6 x+12 y+4=0\)
- Answer
-
1. \((x+2)^{2}+(y-1)^{2}=9\);
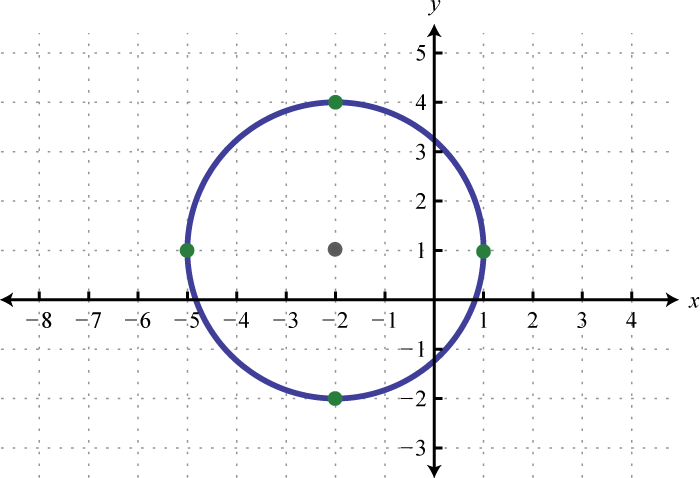
Figure \(\PageIndex{20}\) 3. \((x+1)^{2}+(y+6)^{2}=1\);

Figure \(\PageIndex{21}\) 5. \(x^{2}+(y+3)^{2}=4\);
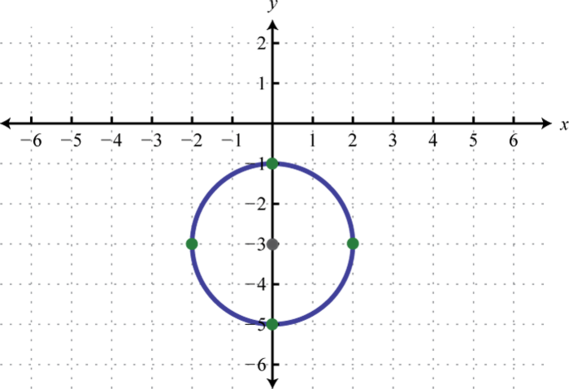
Figure \(\PageIndex{22}\) 7. \((x+4)^{2}+(y+6)^{2}=36\);
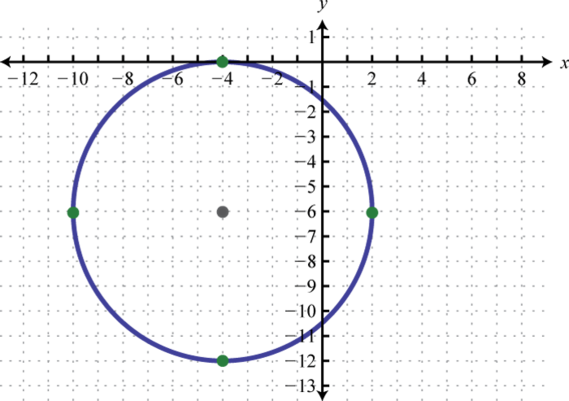
Figure \(\PageIndex{23}\) 9. \(\left(x-\frac{1}{2}\right)^{2}+(y+1)^{2}=1\);
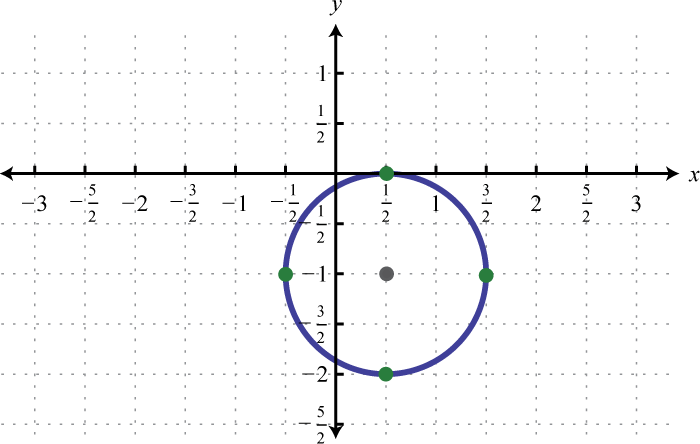
Figure \(\PageIndex{24}\) 11. \((x+2)^{2}+(y-4)^{2}=6\);
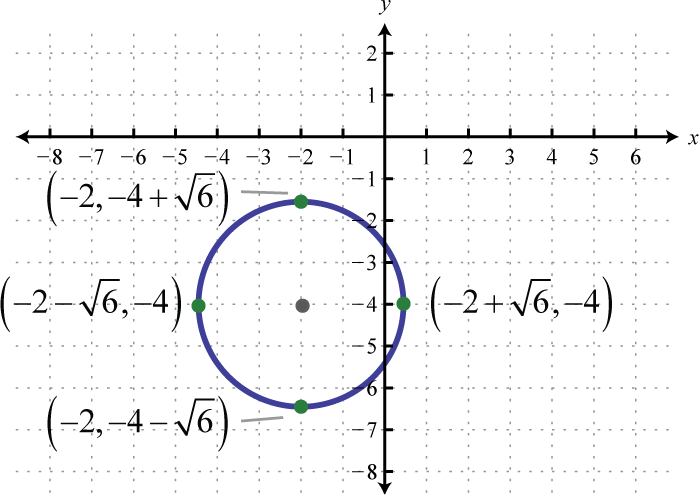
Figure \(\PageIndex{25}\) 13. \(\left(x-\frac{1}{2}\right)^{2}+(y-1)^{2}=\frac{1}{4}\);
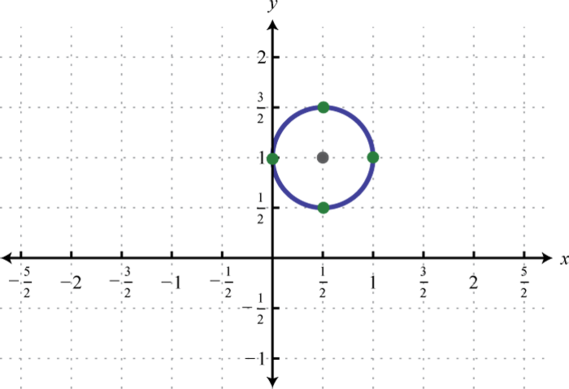
Figure \(\PageIndex{26}\) 15.\((x+1)^{2}+\left(y-\frac{3}{2}\right)^{2}=2\);
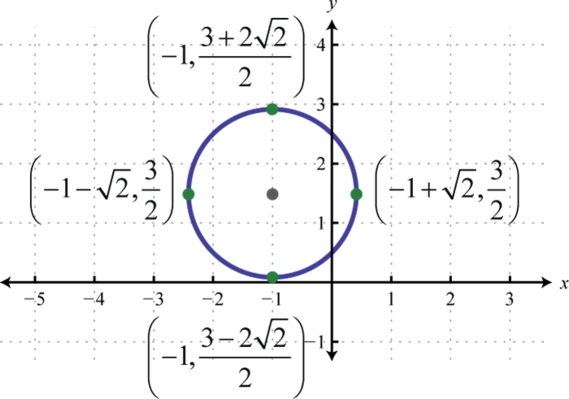
Figure \(\PageIndex{27}\) 17. \(\left(x+\frac{3}{2}\right)^{2}+\left(y+\frac{5}{2}\right)^{2}=4\);
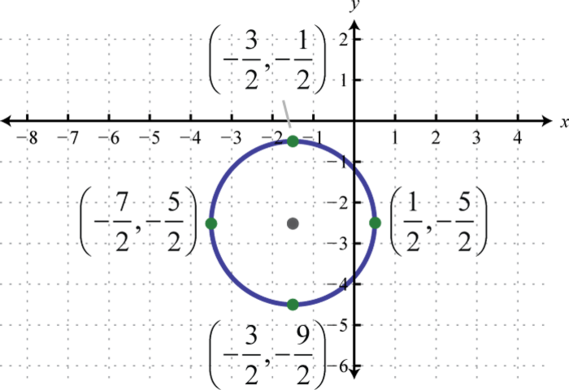
Figure \(\PageIndex{28}\)
Exercise \(\PageIndex{9}\)
Given a circle in general form, determine the intercepts.
- \(x^{2}+y^{2}-5 x+3 y+6=0\)
- \(x^{2}+y^{2}+x-2 y-7=0\)
- \(x^{2}+y^{2}-6 y+2=2\)
- \(x^{2}+y^{2}-6 x-8 y+5=0\)
- \(2 x^{2}+2 y^{2}-3 x-9=0\)
- \(3 x^{2}+3 y^{2}+8 y-16=0\)
- Determine the area of the circle whose equation is \(x^{2}+y^{2}-2 x-6 y-35=0\).
- Determine the area of the circle whose equation is \(4 x^{2}+4 y^{2}-12 x-8 y-59=0\).
- Determine the circumference of a circle whose equation is \(x^{2}+y^{2}-5 x+1=0\).
- Determine the circumference of a circle whose equation is \(x^{2}+y^{2}+5 x-2 y+3=0\).
- Find general form of the equation of a circle centered at \((−3, 5)\) passing through \((1, −2)\).
- Find general form of the equation of a circle centered at \((−2, −3)\) passing through \((−1, 3)\).
- Answer
-
1. \(x\)-intercepts: \((2, 0), (3, 0)\); \(y\)-intercepts: none
3. \(x\)-intercepts: \((0, 0)\); \(y\)-intercepts: \((0, 0), (0, 6)\)
5. \(x\)-intercepts: \((−\frac{3}{2}, 0), (3, 0)\); \(y\)-intercepts: \(\left(0, \pm \frac{3 \sqrt{2}}{2}\right)\)
7. \(45π\) square units
9. \(π\sqrt{21}\) units
11. \(x^{2}+y^{2}+6 x-10 y-31=0\)
Exercise \(\PageIndex{10}\)
Given the graph of a circle, determine its equation in general form.
1.
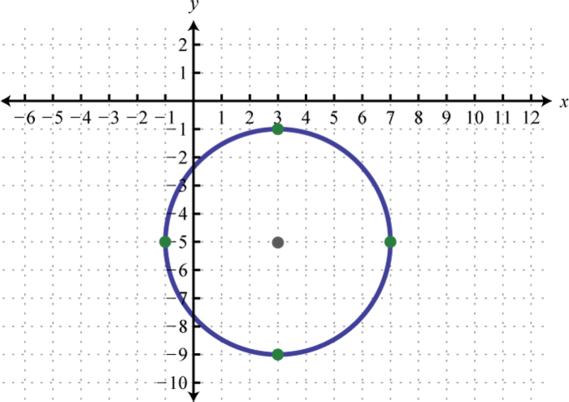
2.

3.
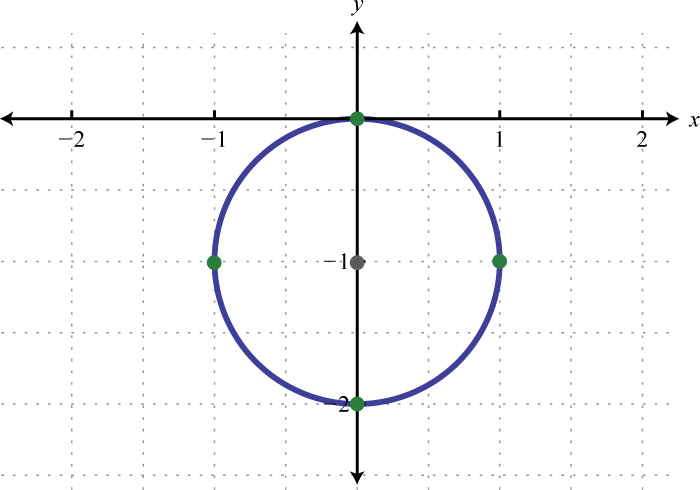
4.

- Answer
-
1. \(x^{2}+y^{2}-6 x+10 y+18=0\)
3. \(x^{2}+y^{2}+2 y=0\)
Exercise \(\PageIndex{11}\)
- Is the center of a circle part of the graph? Explain.
- Make up your own circle, write it in general form, and graph it.
- Explain how we can tell the difference between the equation of a parabola in general form and the equation of a circle in general form. Give an example.
- Do all circles have intercepts? What are the possible numbers of intercepts? Illustrate your explanation with graphs.
- Answer
-
1. Answer may vary
3. Answer may vary
Footnotes
8A circle is the set of points in a plane that lie a fixed distance from a given point, called the center.
9The fixed distance from the center of a circle to any point on the circle.
10The length of a line segment passing through the center of a circle whose endpoints are on the circle.
11The equation of a circle written in the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) where \((h, k)\) is the center and \(r\) is the radius.
12The circle centered at the origin with radius \(1\); its equation is \(x^{2} + y^{2} = 1\).
13The equation of a circle written in the form \(x^{2} + y^{2} + cx + dy + e = 0\).


