13.2: Circles

As we discussed in the previous section, we see a circle is simply a cut from a right circular cone. Let’s discuss the properties of the circle and then graph it.

Definition: Circle

A circle with center \((h, k)\) and radius \(r > 0\) is the set of all points \((x, y)\) in the plane whose distance to \((h, k)\) is \(r\).

Figure 13.2.1

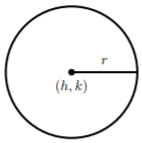
The Standard Equation of a Circle

Let’s take the circle and obtain the standard equation for a circle. We take a point on the circle \((x, y)\) and find the distance from the center to the point. We already know this distance is the radius \(r\), but let’s see algebraically.

Figure 13.2.2

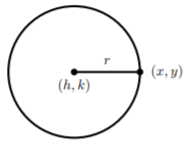
If we apply the distance formula to find the distance between \((h, k)\) and \((x, y)\), we get

\[r=\sqrt{(x-h)^2+(y-k)^2}\nonumber\]

This implies that

\[r^2=(x-h)^2+(y-k)^2\nonumber\]

Hence, by using the distance formula, we obtained the standard equation of a circle.

The Standard Equation of a Circle

The standard equation of a circle with center \((h, k)\) and radius \(r > 0\) is

\[(x-h)^2+(y-k)^2=r^2\nonumber\]

A circle centered at the orogin with radius r is given by

\[x^2+y^2=r^2\nonumber\]

and we can think of \(h\) and \(k\) as horizontal and vertical shifts, respectively, as we did when graphing rational and quadratic functions.

Example 13.2.1

Write the standard equation of the circle with center \((−2, 3)\) and radius \(5\).

Solution

To find the standard equation of the circle with center \((−2, 3)\) and radius \(5\), we can apply the equation above and substitute \(r = 5\), \((h, k) = (−2, 3)\).

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2 \\ (x-\color{blue}{(-2)}\color{black}{)^2}+(y-\color{blue}{3}\color{black}{)}^2&=\color{blue}{5}\color{black}{^2} \\ (x+2)^2+(y-3)^2&=25\end{aligned}\]

Thus, the the standard equation of the circle with center \((−2, 3)\) and radius \(5\) is \((x + 2)^2 + (y − 3)^2 = 25\).

Graph of a Circle from the Standard Equation

Next, we want to graph a circle from the standard equation. Since we can easily identify the center and radius given the standard equation of a circle, we can easily graph the circle.

Example 13.2.2

Graph the circle \((x + 2)^2 + (y − 1)^2 = 4\). Find the center and radius.

Solution

From the standard equation of a circle, we see

\[\begin{aligned} (x-h)^2+(y-k)^2&=r^2 \\ (x+2)^2+(y-1)^2&=4 \\ (x-\color{blue}{(-2)}\color{black}{)}^2+(y-\color{blue}{1}\color{black}{)}^2&=\color{blue}{2}\color{black}{^2}\end{aligned}\]

From looking at the above, we see \(h = −2\), \(k = 1\), and \(r = 2\). This implies we have a circle centered at \((−2, 1)\) with radius \(2\). Let’s graph this information.

First, we plot the center point \((−2, 1)\). Since the distance from the center to any point on the circle is \(2\), then we count two units from the center in each direction. We can connect the points and construct the circle.

Figure 13.2.3

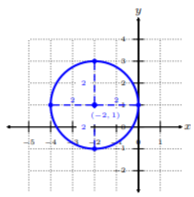
We can see that in order to graph a circle, we need to rewrite, if necessary, the equation of the circle in the standard equation to identify the center and radius. Then we can easily plot the center and count \(r\) units in all four directions to construct the circle.

Rewriting an Equation of a Circle in the Standard Equation Form

What happens when we are given an equation of a circle that isn’t in the form of the standard equation? We can use the method of completing the square to rewrite the equation in the standard equation form.

Recall. To complete the square of a trinomial equation of the form \(x^2 + bx + c = 0\), we can add \(\left(\dfrac{b}{2}\right)^2\) to each side of the equation.

Steps for rewriting an equation of a circle in the standard equation form

Step 1. Group the variable terms together on one side of the equation and position the constant on the opposite side of the equal sign.

Step 2. Complete the square on both variables as needed, i.e., each term should look like \((x − h)^2\) and \((y − k)^2\).

Step 3. If there are coefficients of each factor, then divide each term by the coefficient of the squares.

Example 13.2.3

Find the center and radius of the circle \(x^2 + y^2 − 6x + 8y + 24 = 0\).

Solution

In order to find the center and radius of the circle, we need to rewrite \(x^2 + y^2 − 6x + 8y + 24 = 0\) in the form of the standard equation. Let’s follow the steps to obtain the standard equation form of the given equation of the circle.

Step 1. Group the same variables together on one side of the equation and position the constant on the opposite side of the equal sign.

\[\begin{aligned} x^2+y^2-6x+8y+24&=0 \\ x^2-6x+y^2+8y&=-24\end{aligned}\]

Step 2. Complete the square on both variables as needed, i.e., each term should look like \((x − h)^2\) and \((y − k)^2\).

\[\begin{aligned}x^2-6x+y^2+8y&=-24 \\ x^2-6x\color{blue}{+9}\color{black}{+}y^2+8y\color{blue}{+16}&\color{black}{=}-24\color{blue}{+9+16} \\ (x-3)^2+(y+4)^2&=1\end{aligned}\]

Step 3. Divide both sides by the coefficient of the squares.

Since the coefficients of each factor is 1, then we do not need to reduce out any coefficients.

Notice we obtained the equation \((x−3)^2+(y+4)^2 = 1\). This is the equation \(x^2+y^2−6x+8y+24 = 0\) in its standard equation form. Hence, we can easily obtain the center and radius of the circle. From the standard equation of the circle, we see

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2 \\ (x-3)^2+(y+4)^2&=1 \\ (x-\color{blue}{3}\color{black}{)}^2+(y-\color{blue}{(-4)}\color{black}{)}^2&=\color{blue}{1}\color{black}{^2}\end{aligned}\]

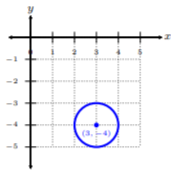
From looking at the above, we see \(h = 3\), \(k = −4\), and \(r = 1\). This implies we have a circle centered at \((3, −4)\) with radius \(1\).

Example 13.2.4

Graph the circle in Example 13.2.3 .

Solution

Since we need to graph the given circle in Example 13.2.3 , we can use the standard equation

\[(x-3)^2+(y+4)^2=1,\nonumber\]

where the circle is centered at \((3, −4)\) with radius \(1\).

First, we plot the center point \((3, −4)\). Since the distance from the center to any point on the circle is 1, then we count one unit from the center in each direction. We can connect the points and construct the circle.

Figure 13.2.4

Example 13.2.5

Write the equation of the circle centered at \((10, 7)\) that passes through \((11, −2)\).

Solution

Since we are given the center of the circle with one point the circle passes, then we can use the standard equation to obtain the radius. Recall, the radius is the distance from the center to a point on the circle.

\[(x-h)^2+(y-k)^2=r^2\nonumber\]

We can plug-n-chug \((h, k) = (10, 7)\) and then \((x, y) = (11, −2)\) to find the radius.

\[\begin{aligned} (x-h)^2+(y-k)^2&=r^2 \\ (11-10)^2+(-2-7)^2&=r^2 \\ 1^2+(-9)^2&=r^2 \\ 1+81&=r^2 \\ \color{red}{82}&\color{black}{=}\color{red}{r^2} \\ \sqrt{82}&=r\end{aligned}\]

Even though the radius isn’t a positive integer, it is still the radius. In fact, if we put the radius in the calculator, we would get \(\sqrt{82}\approx 9.055\). Putting this all together in the standard equation, we get

\[(x-10)^2+(y-7)^2=\color{red}{82}\nonumber\]

Circles Homework

Write the standard equation of the circle and then sketch its graph.

Exercise 13.2.1

Center \((−1, −5)\), radius \(10\)

Exercise 13.2.2

Center \((4, −2)\), radius \(3\)

Exercise 13.2.3

Center \(\left(-3,\dfrac{7}{13}\right)\), radius \(1\)

Rewrite the equation into the standard equation form of a circle. Identify the center and the radius, then sketch a graph. If it the equation is not a circle, state a reason.

Exercise 13.2.4

\(x^2-4x+y^2+10y=-25\)

Exercise 13.2.5

\(-2x^2-36x-2y^2-112=0\)

Exercise 13.2.6

\(x^2+y^2+8x-10y-1=0\)

Exercise 13.2.7

\(x^2+y^2+5x-y-1=0\)

Exercise 13.2.8

\(4x^2+4y^2-24y+36=0\)

Exercise 13.2.9

\(x^2+x+y^2-\dfrac{6}{5}y=1\)

Find the standard equation of the circle which satisfies the given criteria.

Exercise 13.2.10

center \((3, 5)\), passes through \((−1, −2)\)

Exercise 13.2.11

center \((3, 6)\), passes through \((−1, 4)\)

Exercise 13.2.12

endpoints of a diameter: \((3, 6)\) and \((−1, 4)\)

Exercise 13.2.13

endpoints of a diameter: \(\left(\dfrac{1}{2},4\right)\), \(\left(\dfrac{3}{2},-1\right)\)