13.3: Parabolas
- Page ID
- 45125
Recall. The graph of a quadratic function, \(f(x)=ax^2+bx+c\), is a parabola.
As we can see, we either had an upward or downward parabola depending on the leading coefficient, \(a\).
However, in this section, we look at a parabola in terms of its direction. We already discussed the parabola that opens up or down, but, now, let’s look at a parabola that opens left or right:
How do we obtain such parabolas? Let’s start by looking at a basic upwards parabola.
There is a point above the vertex called the focus. The distance from this point to the graph is the same as the distance from a line called the directrix to the same point. In the figure below, the distances \(d_1\) and \(d_2\) are the same, i.e., \(d_1 = d_2\).
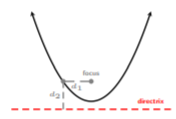
Since the focus and vertex share the same \(x\) coordinate, let’s name the focus point \((h, k + p)\), where \(h\) is the \(x\) coordinate of the vertex and \(k + p\) is the \(y\) coordinate of the focus. If the vertical distance from the vertex to the focus is \(p\), then the directrix is \(k − p\), where \(k\) is the \(y\) coordinate of the vertex.
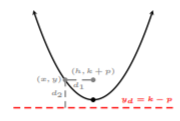
Now, we can find the distance from the focus to any point on the parabola \((x, y)\) by using the distance formula to calculate the distance between points \((x, y)\) to \((h, k + p)\).
Find the distance from a point on a parabola \((x, y)\) to its focus \((0, p)\) with vertex at \((0, 0)\) and directrix at \(y_d = −p\).
Solution
Directly substituting the two points into the distance formula, we get
\[d=\sqrt{(x-0)^2+(y-p)^2}\nonumber\]
Recall, the distance from the focus to any point on the parabola is the same distance from the point to the directrix. Hence, the distance from the point \((x, y)\) to the directrix is \(y−(−p) = y+p\). Let’s substitute this into the distance formula and rewrite the equation in a standard form for a vertical parabola:
\[\begin{aligned} y+p&=\sqrt{x^2+(y-p)^2} \\ (y+p)^2&=x^2+(y-p)^2 \\ y^2+2py+p^2&=x^2+y^2-2yp+p^2 \\ 4yp&=x^2\end{aligned}\]
This the resulting equation is a standard equation of a vertical parabola with vertex at \((0, 0)\).
Generalizing the equation in Example 13.3.1 to any point on a vertical parabola with vertex \((h, k)\), we obtain the standard equation of any vertical parabola with vertex \((h, k)\).
The standard equation of a vertical parabola with vertex \((h, k)\) is
\[(x-h)^2=4p(y-k)\nonumber\]
Continuing, if we apply the same idea to a horizontal parabola, where the directrix is a vertical line and the focus is to the left or right of the vertex, we get
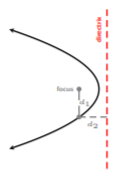
In the figure above, the distances \(d_1\) and \(d_2\) are the same, i.e., \(d_1 = d_2\), as it is with an upward parabola. And so, generalizing an equation for a horizontal parabola with vertex \((h, k)\), we obtain the standard equation of any horizontal parabola with vertex \((h, k)\).
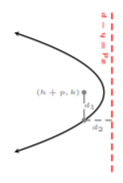
The standard equation of a horizontal parabola with vertex \((h, k)\) is
\[(y-k)^2=4p(x-h)\nonumber\]
Graph a Parabola in Standard Equation Form
In general, a parabola’s direction depends on the location of the directrix and focus. Putting this all together with graphing quadratic functions, we obtain the properties of a parabola.
To graph a parabola, we can use the table to determine the direction and all other properties.
| Equation | Direction | Focus | Directrix | Axis of Symmetry |
|---|---|---|---|---|
| \((x-h)^2=4p(y-k)\) | Upward \((p>0)\) or downward \((p<0)\) | \((h,k+p)\) | \(y=k-p\) | \(x=h\) |
| \((y-k)^2=4p(x-h)\) | Left \((p<0)\) or right \((p>0)\) | \((h+p,k)\) | \(x=h-p\) | \(y=k\) |
Graph the parabola \((x + 1)^2 = −8(y − 3)\). Identify and label the vertex, focus, directrix, and axis of symmetry.
Solution
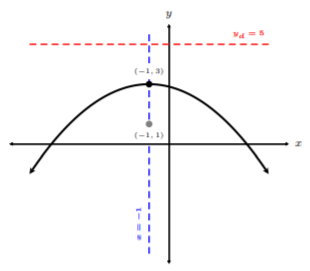
To begin, we can identify the properties, then graph. Right away, we see the vertex is \((−1, 3)\) and the axis of symmetry is \(x = −1\). Since the squared factor contains \(x\), we know this parabola opens upward or downward. Let’s find \(p\) to determine the particular direction.
\[\begin{aligned}(x-h)^2&=\color{blue}{4p}\color{black}{(}y-k) \\ (x+1)^2&=\color{blue}{-8}\color{black}{(}y-3)\end{aligned}\]
We can see from the given equation and standard equation, \(4p = −8\). This implies that \(p = −2\). Since \(p = −2 < 0\), the parabola will open downward. From knowing \(p = −2\), we can find the focus and directrix:
Focus:
\[\begin{array}{r}(h,k+p) \\ (-1,3+(-2)) \\ (-1,1)\end{array}\nonumber\]
The focus point is \((−1, 1)\).
Directrix:
\[\begin{aligned}y&=k-p \\ y&=3-(-2) \\ y&=5\end{aligned}\]
The directrix is the line \(y = 5\). We are now ready to graph the parabola with the vertex at \((−1, 3)\), axis of symmetry \(x = −1\), focus point at \((−1, 1)\), and directrix \(y = 5\).
Rewriting an Equation of a Parabola in the Standard Equation Form
Sometimes we aren’t given a parabola in its standard equation form. Hence, we have to rewrite the equation so the equation of the parabola is in the standard equation. We can do this by completing the square on the term that is squared.
Recall. To complete the square of a trinomial equation of the form \(x^2 + bx + c = 0\), we can add \(\left(\dfrac{b}{2}\right)^2\) to each side of the equation.
Step 1. Group the variable which is squared on one side of the equation and position the nonsquared variable and the constant on the other side.
Step 2. Complete the square, if necessary, and divide by the coefficient of the perfect square, i.e., the squared term should like \((x − h)^2\) or \((y − k)^2\).
Step 3. Factor out the coefficient of the non-squared variable and the constant.
Consider the equation of the parabola \(y^2 + 4y + 8x = 4\). Rewrite this equation in the standard equation form and graph the parabola. Find and label the vertex, focus, directrix, and axis of symmetry.
Solution
In order to find the properties of the parabola, we need to rewrite \(y^2 + 4y + 8x = 4\) in the form of the standard equation. Let’s follow the steps to obtain the standard equation form of the given equation of the parabola.
Step 1. Group the variable which is squared on one side of the equation and position the non-squared variable and the constant on the other side.
We notice the term \(y^2\). Since the \(y\) is the squared term, then we know this parabola opens left or right.
\[\begin{aligned}y^2+4y+8x&=4 \\ y^2+4y&=-8x+4\end{aligned}\]
Step 2. Complete the square, if necessary, and divide by the coefficient of the perfect square.
\[\begin{aligned} y^2+4y&=-8x+4 \\ y^2+4y\color{blue}{+4}&\color{black}{=}-8x+4\color{blue}{+4} \\ y^2+4y+4&=-8x+8 \\ (y+2)^2&=-8x+8\end{aligned}\]
Step 3. Factor out the coefficient of the non-squared variable and the constant.
\[\begin{aligned} (y+2)^2&=-8x+8 \\ (y+2)^2&=-8(x-1)\end{aligned}\]
Hence, the parabola \(y^2 + 4y + 8x = 4\) in its standard equation is \((y + 2)^2 = −8(x−1)\). Next, let’s identify all the properties to graph. We can easily see that the vertex is \((1, −2)\) and the axis of symmetry is \(y = −2\). We need to find \(p\) to obtain the focus and directrix. We can see from the given equation and standard equation, \(4p = −8\). This implies that \(p = −2\). Since \(p = −2 < 0\), the parabola will open to the left. From knowing \(p = −2\), we can find the focus and directrix:
Focus:
\[\begin{array}{r}(h+p,k) \\ (1+(-2),-2) \\ (-1,-2) \end{array}\nonumber\]
The focus point is \((-1,-2)\).
Directrix:
\[\begin{aligned} x&=h-p \\ x&=1-(-2) \\ x&=3\end{aligned}\]
The directrix is the line \(x = 3\). We are now ready to graph the parabola with the vertex at \((1, −2)\), axis of symmetry \(y = −2\), focus point at \((−1, −2)\), and directrix \(x = 3\).
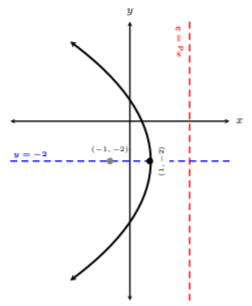
Thus, the graph above is the graph of \((y + 2)^2 = −8(x − 1)\).
Parabolas Homework
Sketch the graph of each parabola. Find the vertex, focus, directrix, and axis of symmetry.
\((x-3)^2=-16y\)
\(\left(x+\dfrac{7}{3}\right)^2=2\left(y+\dfrac{5}{2}\right)\)
\((y-2)^2=-12(x+3)\)
\((y+4)^2=4x\)
\((x-1)^2=4(y+3)\)
\((x+2)^2=-20(y-5)\)
\((y-4)^2=18(x-2)\)
\(\left(y+\dfrac{3}{2}\right)^2=-7\left(x+\dfrac{9}{2}\right)\)
Rewrite the equation of the parabola into its standard equation form and identify the vertex, focus, directrix, and axis of symmetry. Then sketch the graph.
\(x^2+2x-8y+49=0\)
\(3y^2-27y+4x+\dfrac{211}{4}=0\)
\(2y^2+4y+x-8=0\)
\(x^2-10x+12y+1=0\)


