13.4: Introduction to Conics- Answers to the Homework Exercises

Last updated
Save as PDF

Page ID: 45126

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introduction to Conics

$\left(0,\dfrac{1}{2}\right)$; $\sqrt{109}\approx 10.44$

$\left(-\dfrac{1}{2},-\dfrac{3}{2}\right)$; $\sqrt{34}\approx 5.83$

$\left(\dfrac{185}{2},-69\right)$; $41$

circle

ellipse

parabola

parabola

Circles

$(x+1)^2+(y+5)^2=100$
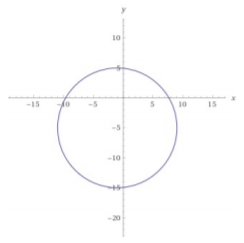
$clipboard_e2daa35634f0d90ea4180c59fb0414183.png$
Figure 13.4.1

$(x+3)^2+\left(y-\dfrac{7}{13}\right)^2=\dfrac{1}{4}$
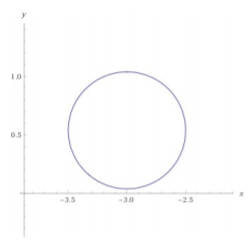
$clipboard_e768f1240e6276acda885c9d9e032c77c.png$
Figure 13.4.2

$(x+9)^2+y^2=25$; center $(-9,0)$, radius $r=5$
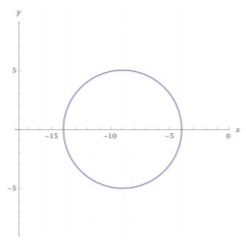
$clipboard_eb22b0537bc1cd95fb115438068d6abf7.png$
Figure 13.4.3

$\left(x+\dfrac{5}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{30}{4}$; center $\left(-\dfrac{5}{2},\dfrac{1}{2}\right)$, radius $r=\dfrac{\sqrt{30}}{2}$
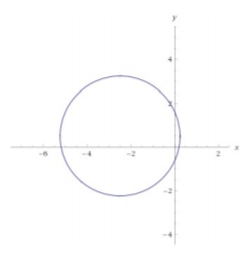
$clipboard_e27e1b5abe53502c73483aabb6de7ac6a.png$
Figure 13.4.4

$\left(x+\dfrac{1}{2}\right)^2+\left(y-\dfrac{3}{5}\right)^2=\dfrac{161}{100}$; center $\left(-\dfrac{1}{2},\dfrac{3}{5}\right)$, radius $r=\dfrac{\sqrt{161}}{10}$
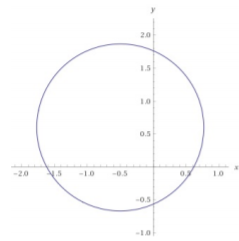
$clipboard_e48ea4b708e6e51e741d3546bacbebf60.png$
Figure 13.4.5

$(x-3)^2+(y-6)^2=20$

$(x-1)^2+\left(y-\dfrac{3}{2}\right)^2=\dfrac{13}{2}$

Parabolas

Vertex $(3,0)$; Focus $(3,-4)$; Directrix $y=4$
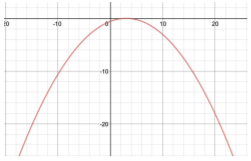
$clipboard_e6548057fdda420a45893ccba380f6787.png$
Figure 13.4.6

Vertex $(-3,2)$; Focus $(-6,2)$; Directrix $x=0$
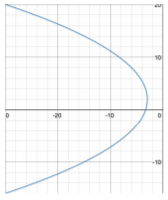
$clipboard_eaa495579a3d2b13cdfab0a89bbaa9500.png$
Figure 13.4.7

Vertex $(1,-3)$; Focus $(1,-2)$; Directrix $y=-4$
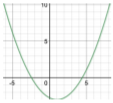
$clipboard_ed327db463912a90f3ec9a28f1898bbb2.png$
Figure 13.4.8

Vertex $(2,4)$; Focus $\left(\dfrac{13}{2},4\right)$; Directrix $x=-\dfrac{5}{2}$
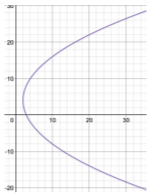
$clipboard_e6f71ae9faee62fe289f7aa215019d4be.png$
Figure 13.4.9

$(x+1)^2=8(y-6)$; Vertex $(-1,6)$; Focus $(-1,8)$; Directrix $y=4$
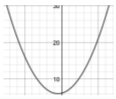
$clipboard_e436d72e3336e0a259b565f0254e84164.png$
Figure 13.4.10

$(y+1)^2=-\dfrac{1}{2}(x-10)$; Vertex $(10,-1)$; Focus $\left(\dfrac{79}{8},-1\right)$; Directrix $x=\dfrac{81}{8}$
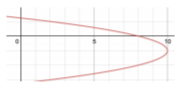
$clipboard_e1616b4c5ffc259dbaa5dbcb832ed3d55.png$
Figure 13.4.11