Skip to main content
Library homepage
 

Text Color

Text Size

 

Margin Size

 

Font Type

Enable Dyslexic Font
Mathematics LibreTexts

8.3: Ellipses

  1. CCBYNCSA
  2. Last updated
    Oct 6, 2021
  3. Save as PDF
  • Anonymous
  • LibreTexts

( \newcommand{\kernel}{\mathrm{null}\,}\)

Learning Objectives

  • Graph an ellipse in standard form.
  • Determine the equation of an ellipse given its graph.
  • Rewrite the equation of an ellipse in standard form.

The Ellipse in Standard Form

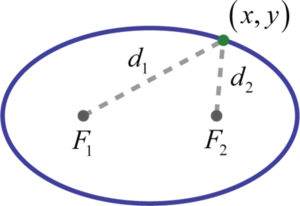
An ellipse14 is the set of points in a plane whose distances from two fixed points, called foci, have a sum that is equal to a positive constant. In other words, if points and are the foci (plural of focus) and is some given positive constant then is a point on the ellipse if as pictured below:

imageedit_2_2910588286.png
Figure

In addition, an ellipse can be formed by the intersection of a cone with an oblique plane that is not parallel to the side of the cone and does not intersect the base of the cone. Points on this oval shape where the distance between them is at a maximum are called vertices15 and define the major axis16. The center of an ellipse is the midpoint between the vertices. The minor axis17 is the line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is at a minimum. The endpoints of the minor axis are called co-vertices18.

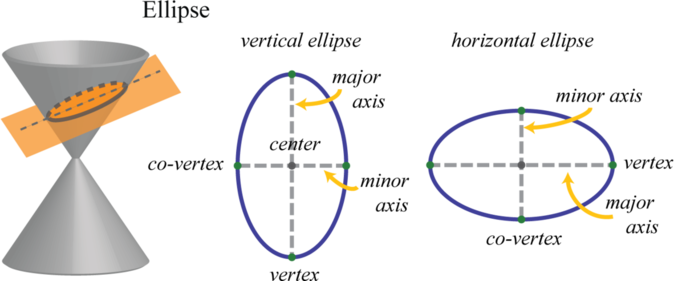
imageedit_42_6771649286.png
Figure

If the major axis of an ellipse is parallel to the -axis in a rectangular coordinate plane, we say that the ellipse is horizontal. If the major axis is parallel to the -axis, we say that the ellipse is vertical. In this section, we are only concerned with sketching these two types of ellipses. However, the ellipse has many real-world applications and further research on this rich subject is encouraged. In a rectangular coordinate plane, where the center of a horizontal ellipse is , we have

imageedit_9_5816222250.png
Figure

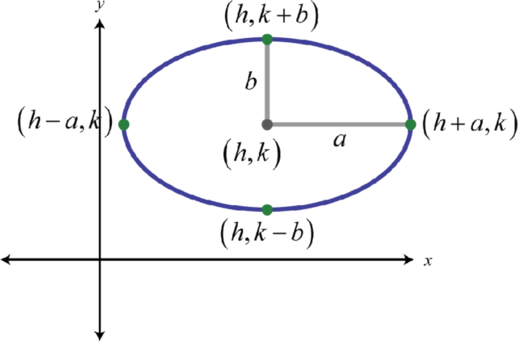
As pictured where , one-half of the length of the major axis, is called the major radius19. And , one-half of the length of the minor axis, is called the minor radius20. The equation of an ellipse in standard form21 follows:

The vertices are and and the orientation depends on and . If , then the ellipse is horizontal as shown above and if , then the ellipse is vertical and becomes the major radius. What do you think happens when ?

Table
Equation Center Orientation
Vertical
Vertical
Vertical
Horizontal

The graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius, all of which can be determined from its equation written in standard from.

Example :

Graph: .

Solution

Written in this form we can see that the center of the ellipse is , , and . From the center mark points 2 units to the left and right and 5 units up and down.

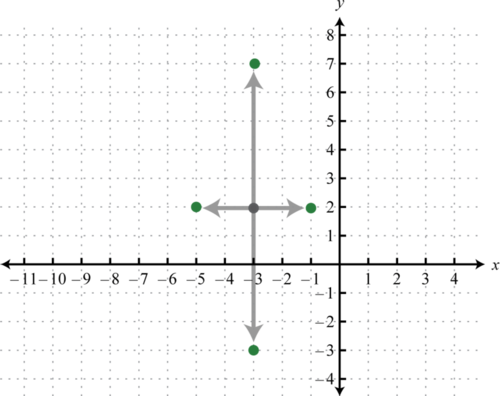
imageedit_46_9665036689.png
Figure

Then draw an ellipse through these four points.

Answer

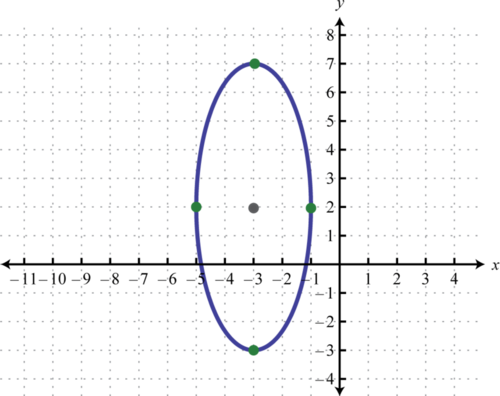
imageedit_17_5171480346.png
Figure

As with any graph, we are interested in finding the - and -intercepts.

Example

Find the intercepts: .

Solution

To find the -intercepts set :

At this point we extract the root by applying the square root property.

Setting and solving for leads to complex solutions, therefore, there are no -intercepts. This is left as an exercise.

Answer:

-intercepts: ; -intercepts: none.

Unlike a circle, standard form for an ellipse requires a on one side of its equation.

Example :

Graph and label the intercepts: .

Solution

To obtain standard form, with on the right side, divide both sides by .

Therefore, the center of the ellipse is , , and . The graph follows:

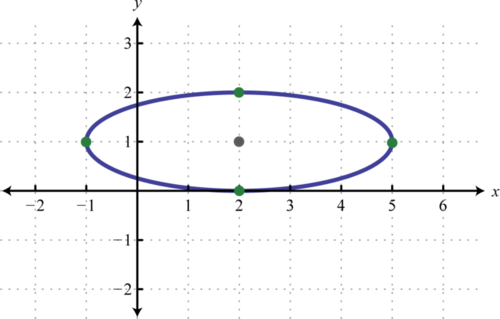
imageedit_21_6941829446.png
Figure

To find the intercepts we can use the standard form :

-intercepts set -intercepts set
Table

Therefore the -intercept is and the -intercepts are and .

Answer:

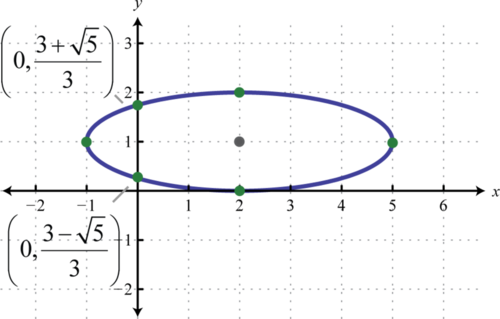
imageedit_25_3510451197.png
Figure

Consider the ellipse centered at the origin,

Given this equation we can write,

In this form, it is clear that the center is , , and . Furthermore, if we solve for we obtain two functions:

The function defined by is the top half of the ellipse and the function defined by is the bottom half.

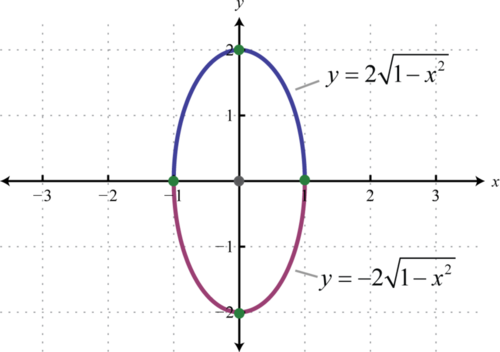
imageedit_29_7484993562.png
Figure

Exercise

Graph: .

Answer
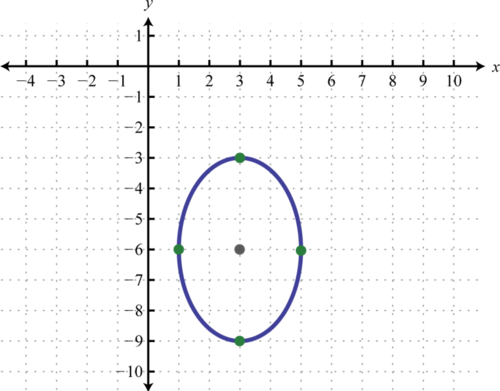
imageedit_54_3427818305.png
Figure

The Ellipse in General Form

We have seen that the graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius; which can be read from its equation in standard form. However, the equation is not always given in standard form. The equation of an ellipse in general form22 follows,

where . The steps for graphing an ellipse given its equation in general form are outlined in the following example.

Example :

Graph .

Solution

Begin by rewriting the equation in standard form.

Step 1: Group the terms with the same variables and move the constant to the right side. Factor so that the leading coefficient of each grouping is .

Step 2: Complete the square for each grouping. In this case, for the terms involving use and for the terms involving use . The factor in front of the grouping affects the value used to balance the equation on the right side:

Because of the distributive property, adding inside of the first grouping is equivalent to adding . Similarly, adding inside of the second grouping is equivalent to adding . Now factor and then divide to obtain on the right side.

Step 3: Determine the center, , and . In this case, the center is , , and .

Step 4: Use a to mark the vertices left and right of the center, use b to mark the vertices up and down from the center, and then sketch the graph. In this case, the vertices along the minor axes are not apparent and should be labeled.

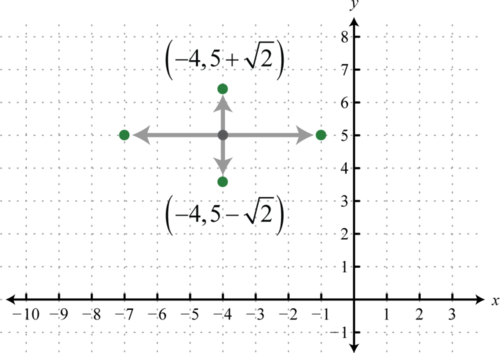
imageedit_33_4965084120.png
Figure

Answer:

imageedit_37_9255639646.png
Figure

Example :

Determine the center of the ellipse as well as the lengths of the major and minor axes: .

Solution

In this example, we only need to complete the square for the terms involving .

Use for the first grouping to be balanced by on the right side.

Here, the center is , , and . Because is larger than , the length of the major axis is and the length of the minor axis is .

Answer

Center: ; major axis: 2 units; minor axis: units.

Exercise

Graph .

Answer
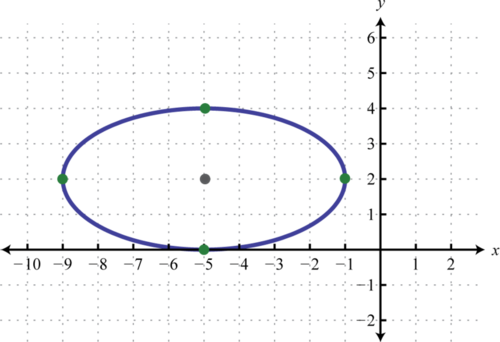
imageedit_50_4103884015.png
Figure

www.youtube.com/v/Mhp7S5H2820

Key Takeaways

  • The graph of an ellipse is completely determined by its center, orientation, major radius, and minor radius.
  • The center, orientation, major radius, and minor radius are apparent if the equation of an ellipse is given in standard form: .
  • To graph an ellipse, mark points units left and right from the center and points units up and down from the center. Draw an ellipse through these points.
  • The orientation of an ellipse is determined by and . If then the ellipse is wider than it is tall and is considered to be a horizontal ellipse. If a<ba<b then the ellipse is taller than it is wide and is considered to be a vertical ellipse.
  • If the equation of an ellipse is given in general form where , group the terms with the same variables, and complete the square for both groupings.
  • We recognize the equation of an ellipse if it is quadratic in both and and the coefficients of each square term have the same sign.

Exercise

Given the equation of an ellipse in standard form, determine its center, orientation, major radius, and minor radius.

Answer

1. Center: ; orientation: vertical; major radius: units; minor radius: units;

3. Center: ; orientation: horizontal; major radius: units; minor radius: unit;

5. Center: ; orientation: horizontal; major radius: units; minor radius: units;

Exercise

Determine the standard form for the equation of an ellipse given the following information.

  1. Center with and .
  2. Center with and .
  3. Center with and .
  4. Center with and .
  5. Center with and .
  6. Center with and .
Answer

1.

3.

5.

Exercise

Graph.

Answer

1.

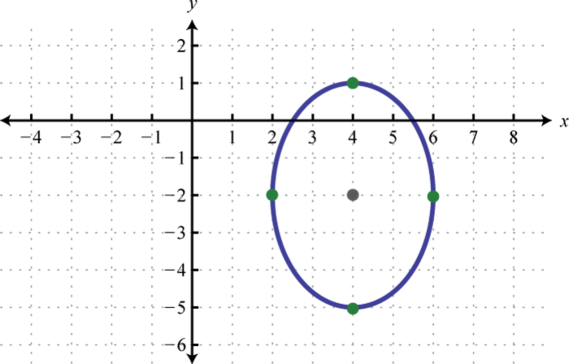
b53958ca303afa5b0c216db50472aebb.png
Figure

3.

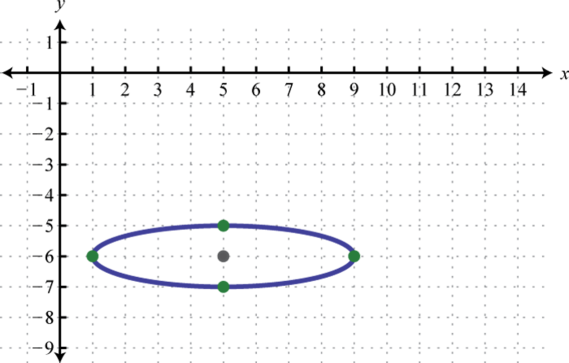
9e9f5466ae3f031b917897e4315b4816.png
Figure

5.

9550eaa6151dedb4804fa71c8162d62b.png
Figure

7.

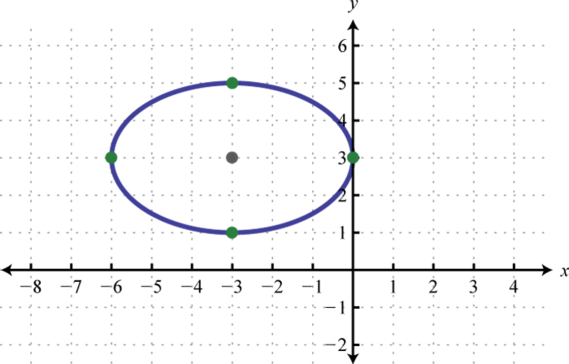
a8dfca7c363ba28d06abed6999e569ec.png
Figure

9.

4c700e9ed1a845edbac9eb60275b3202.png
Figure

11.

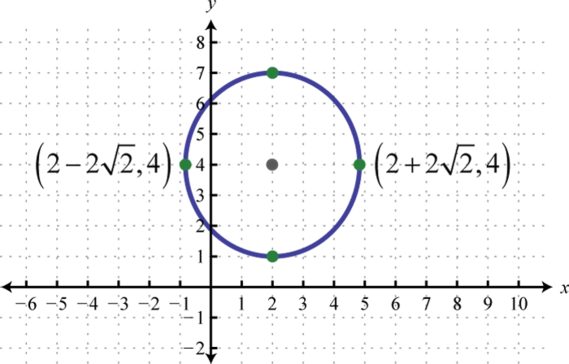
ed88c51ce575a7dc93ed701c40cfd9ea.png
Figure

13.

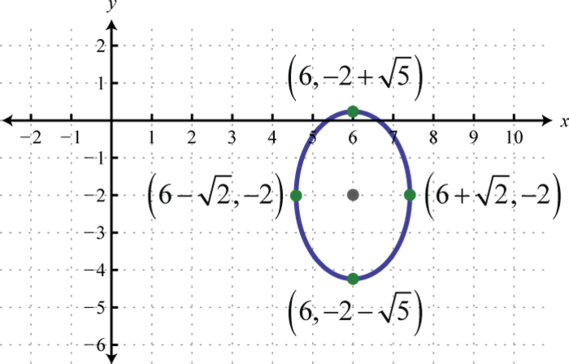
332680ad079811d8813e1bb55d43f296.png
Figure

15.

bd9b328604d51df0b1c3e2f694d572b5.png
Figure

17.

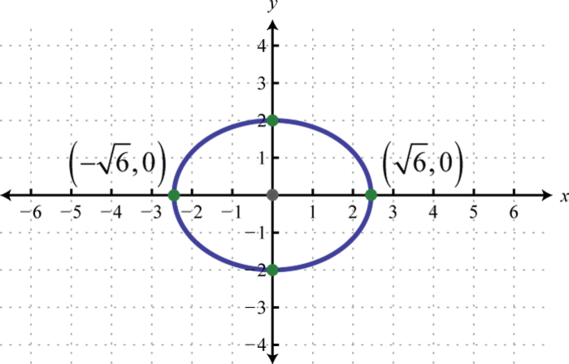
bed8a3eb995e00138c387e98b8da9cc8.png
Figure

Exercise

Find the - and -intercepts.

Answer

1. -intercepts: ;-intercepts: none

3. -intercepts: ;-intercepts:

5. -intercepts: none;-intercepts:

7. -intercepts: ;-intercepts:

Exercise

Find the equation of the ellipse.

  1. Ellipse with vertices and .
  2. Ellipse whose major axis has vertices and and minor axis has vertices and .
  3. Ellipse whose major axis has vertices and and minor axis has a length of units.
  4. Ellipse whose major axis has vertices and and minor axis has a length of units.
Answer

1.

3.

Exercise

Rewrite in standard form and graph.

Answer

1. ;

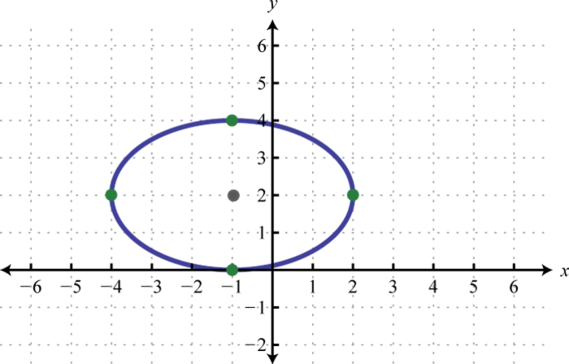
5bd9952171df55c084e928d02b08eb44.png
Figure

3. ;

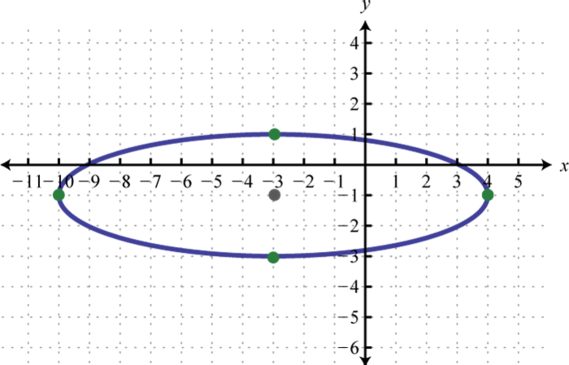
a9cb7f3ac696205a2b2bcb127773e732.png
Figure

5. ;

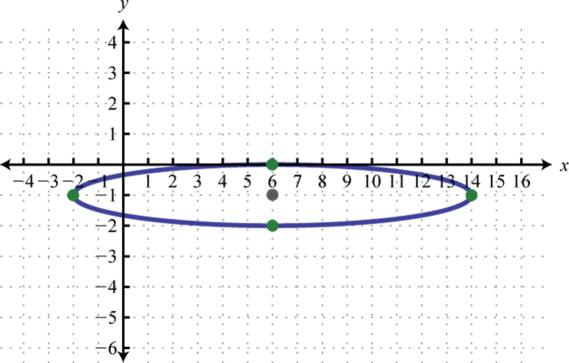
bddde005efa3182e493c27ff31bf1287.png
Figure

7. ;

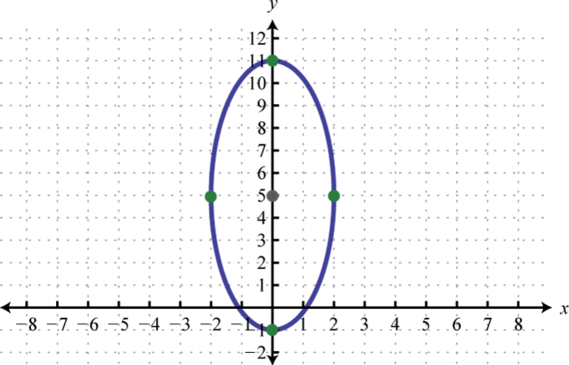
167ea4159775aea700b99fc79ec30dce.png
Figure

9. ;

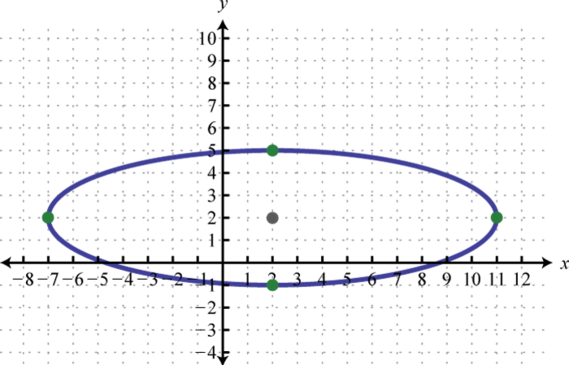
d6bcee76aa5ce3f1a490200e1b772b3b.png
Figure

11. ;

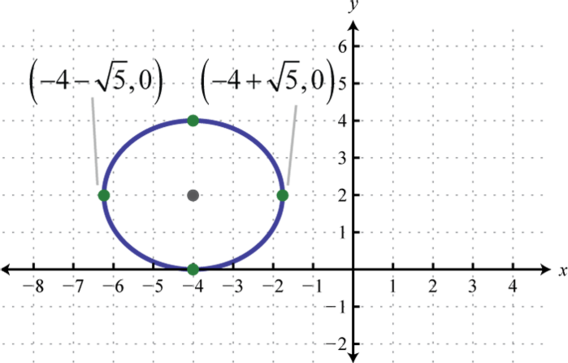
77a4c994e2d4b186bdc90501bb222350.png
Figure

13. ;

e68d7473c5e235db17f8697762822b6a.png
Figure

15. ;

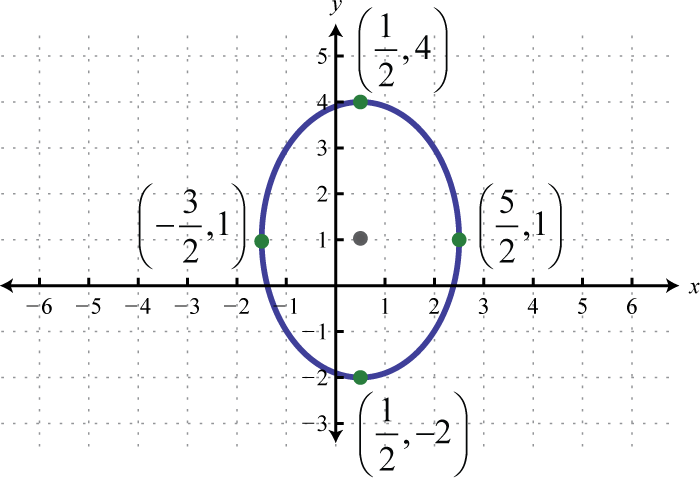
f782675735c2a1f76923e6003805f093.png
Figure

17. ;

24b81e7d0d85d4cc0f50ed345e158e3b.png
Figure

Exercise

Given general form determine the intercepts.

Answer

1. -intercepts: none; -intercepts:

3. -intercepts: ; -intercepts:

5. -intercepts: ; -intercepts: none

Exercise

Determine the area of the ellipse. (The area of an ellipse is given by the formula , where and are the lengths of the major radius and the minor radius.)

Answer

1. square units

3. square units

Exercise

Given the graph of an ellipse, determine its equation in general form.

1.

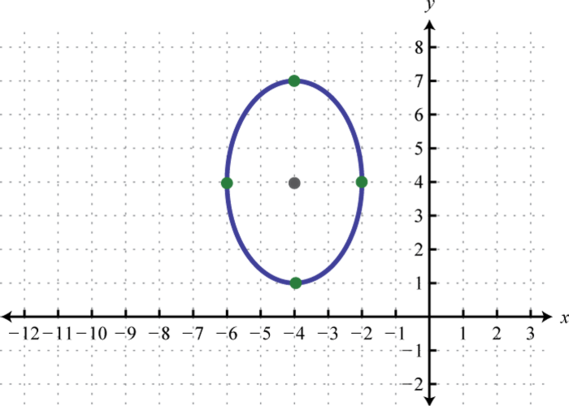
77d9ec6f401101fb60445904c2b9e5cf.png
Figure

2.

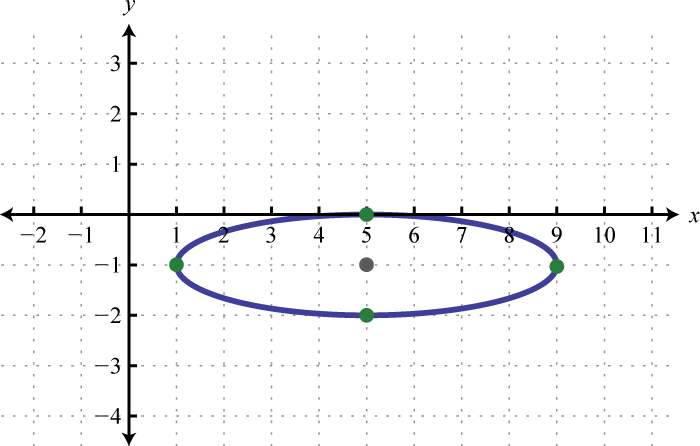
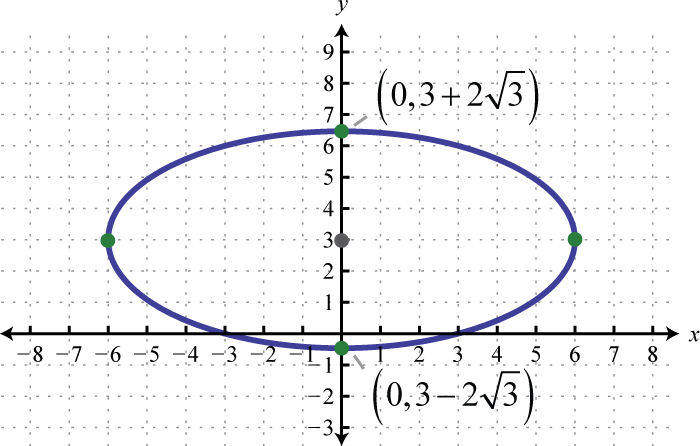
ceaac1c27ebfdacf70c398411757869c.png
Figure

3.

cf3ead1d53975e6c36e7b4995c1f92f3.png
Figure

4.

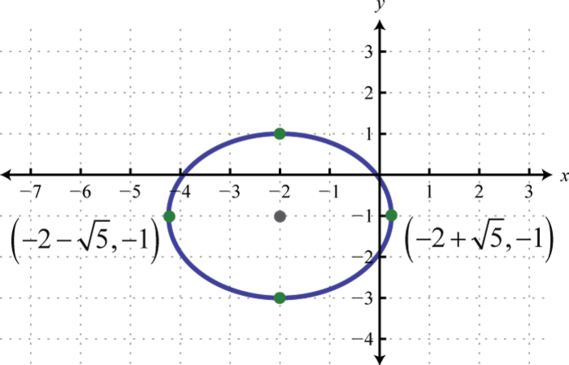
c0a66b6a01cd2a053bab9800d805b634.png
Figure
Answer

1.

3.

Exercise

  1. Explain why a circle can be thought of as a very special ellipse.
  2. Make up your own equation of an ellipse, write it in general form and graph it.
  3. Do all ellipses have intercepts? What are the possible numbers of intercepts for an ellipse? Explain.
  4. Research and discuss real-world examples of ellipses.
Answer

1. Answer may vary

3. Answer may vary

Footnotes

14The set of points in a plane whose distances from two fixed points have a sum that is equal to a positive constant.

15Points on the ellipse that mark the endpoints of the major axis.

16The line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is a maximum.

17The line segment through the center of an ellipse defined by two points on the ellipse where the distance between them is a minimum.

18Points on the ellipse that mark the endpoints of the minor axis.

19One-half of the length of the major axis.

20One-half of the length of the minor axis.

21The equation of an ellipse written in the form .The center is and the larger of and is the major radius and the smaller is the minor radius.

22The equation of an ellipse written in the form where .

This page titled 8.3: Ellipses is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by Anonymous via source content that was edited to the style and standards of the LibreTexts platform.

  1. Back to top
  • Was this article helpful?

Recommended articles

  1. 8.2: The EllipseThe key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other...
  2. 12.1: The EllipseThe key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other...
  3. 8.2: The EllipseThe key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other...
  4. 12.2: The EllipseThe key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other...
  5. 8.2: The EllipseThe key features of the ellipse are its center, vertices, co-vertices, foci, and lengths and positions of the major and minor axes. Just as with other...
  1. Article type
    Section or Page
    Author
    Anonymous
    License
    CC BY-NC-SA
    License Version
    3.0
    OER program or Publisher
    The Publisher Who Must Not Be Named
    Show Page TOC
    no
  2. Tags
    1. ellipses
    2. foci
    3. major axis
    4. minor axis
    5. source@https://2012books.lardbucket.org/books/advanced-algebra/index.html

Support Center

How can we help?