3.8: Linear Inequalities (Two Variables)
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identify and check solutions to linear inequalities with two variables.
- Graph solution sets of linear inequalities with two variables.
Solutions to Linear Inequalities
We know that a linear equation with two variables has infinitely many ordered pair solutions that form a line when graphed. A linear inequality with two variables, on the other hand, has a solution set consisting of a region that defines half of the plane.
| Linear Equation | Linear Inequality |
|---|---|
|
Figure |
Figure |
For the inequality, the line defines one boundary of the region that is shaded. This indicates that any ordered pair that is in the shaded region, including the boundary line, will satisfy the inequality. To see that this is the case, choose a few test points and substitute them into the inequality.
Also, we can see that ordered pairs outside the shaded region do not solve the linear inequality.
The graph of the solution set to a linear inequality is always a region. However, the boundary may not always be included in that set. In the previous example, the line was part of the solution set because of the “or equal to” part of the inclusive inequality
| Non-Inclusive Boundary | Inclusive Boundary |
|---|---|
|
Figure |
Figure |
Consider the point
So far, we have seen examples of inequalities that were “less than.” Now consider the following graphs with the same boundary:
| Greater Than (Above) | Less Than (Below) |
|---|---|
|
Figure |
Figure |
Given the graphs above, what might we expect if we use the origin
Which of the ordered pairs
- Answer
-
Graphing Solutions to Linear Inequalities
Solutions to linear inequalities are a shaded half-plane, bounded by a solid line or a dashed line. This boundary is either included in the solution or not, depending on the given inequality. If we are given a strict inequality, we use a dashed line to indicate that the boundary is not included. If we are given an inclusive inequality, we use a solid line to indicate that it is included. The steps for graphing the solution set for an inequality with two variables are outlined in the following example.
Graph the solution set:
Solution:
Step 1: Graph the boundary line. In this case, graph a dashed line
.png?revision=1)
Figure
Step 2: Test a point not on the boundary. A common test point is the origin
Step 3: Shade the region containing the solutions. Since the test point
Answer:
.png?revision=1)
Figure
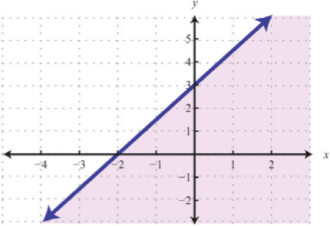
Consider the problem of shading above or below the boundary line when the inequality is in slope-intercept form. If
Graph the solution set:
Solution:
Here the boundary is defined by the line
.png?revision=1)
Figure
Next, test a point; this helps decide which region to shade.
Since the test point is in the solution set, shade the half of the plane that contains it.
Answer:
.png?revision=1)
Figure
In this example, notice that the solution set consists of all the ordered pairs below the boundary line. This may be counterintuitive because of the original
In slope-intercept form, you can see that the region below the boundary line should be shaded. An alternate approach is to first express the boundary in slope-intercept form, graph it, and then shade the appropriate region.
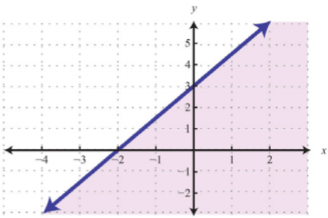
Example
Graph the solution set:
Solution:
First, graph the boundary line
.png?revision=1)
Figure
Now, test a point.
In this case, shade the region that contains the test point.
Answer:
.png?revision=1)
Figure
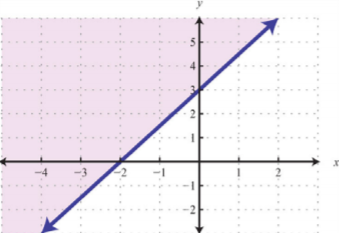
Graph the solution set:
- Answer
-
.png?revision=1)
Figure
Key Takeaways
- Linear inequalities with two variables have infinitely many ordered pair solutions, which can be graphed by shading in the appropriate half of a rectangular coordinate plane.
- To graph the solution set of a linear inequality with two variables, first graph the boundary with a dashed or solid line depending on the inequality. If given a strict inequality, use a dashed line for the boundary. If given an inclusive inequality, use a solid line. Next, choose a test point not on the boundary. If the test point solves the inequality, then shade the region that contains it; otherwise, shade the opposite side.
- When graphing the solution sets of linear inequalities, it is a good practice to test values in and out of the solution set as a check.
Is the ordered pair a solution to the given inequality?
- Answer
-
1. Yes
3. Yes
5. Yes
7. No
9. Yes
Graph the solution set.
- Write an inequality that describes all points in the upper half-plane above the
- Write an inequality that describes all points in the lower half-plane below the
- Write an inequality that describes all points in the half-plane left of the
- Write an inequality that describes all points in the half-plane right of the
- Write an inequality that describes all ordered pairs whose
- Write an inequality that describes all ordered pairs whose
- Answer
-
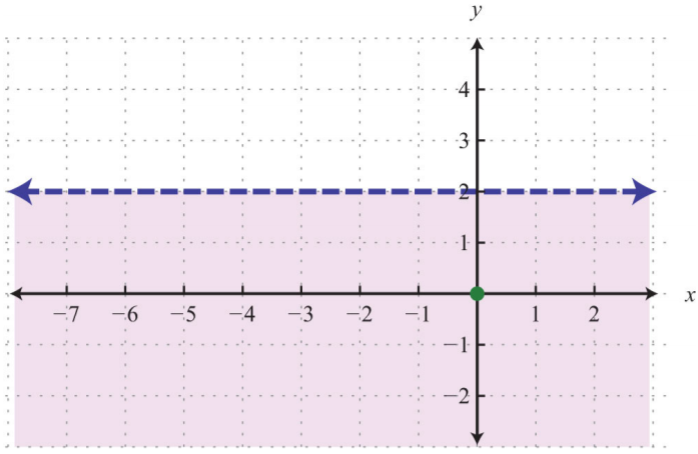
1.
.png?revision=1)
Figure
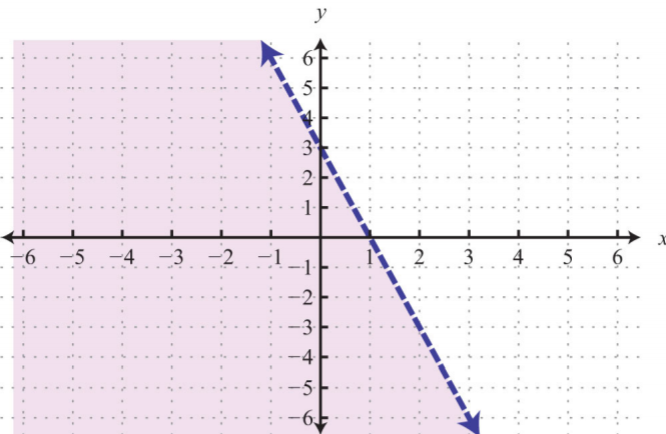
3.
.png?revision=1)
Figure
5.
.png?revision=1)
Figure
7.
.png?revision=1)
Figure
9.
.png?revision=1)
Figure
11.
.png?revision=1)
Figure
13.
.png?revision=1)
Figure
15.
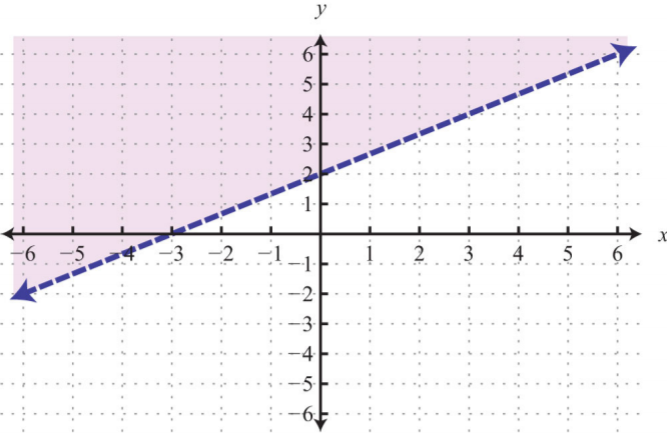.png?revision=1)
Figure
17.
.png?revision=1)
Figure
19.
.png?revision=1)
Figure
21.
.png?revision=1)
Figure
23.
.png?revision=1)
Figure
25.
.png?revision=1)
Figure
27.
.png?revision=1)
Figure
29.
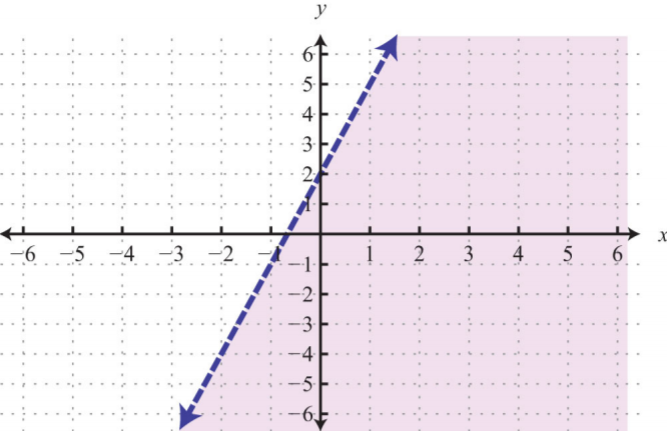.png?revision=1)
Figure
31.
.png?revision=1)
Figure
33.
35.
37.



.png?revision=1)
.png?revision=1)
.png?revision=1)
.png?revision=1)
.png?revision=1)
.png?revision=1)