3.3: Graph Using Intercepts
- Page ID
- 18342
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identify and find \(x\)- and \(y\)-intercepts of a graph.
- Graph a line using \(x\)- and \(y\)-intercepts
Definition of \(x\)- and \(y\)-intercepts
The \(x\)-intercept is the point where the graph of a line intersects the \(x\)-axis.
The \(y\)-intercept is the point where the graph of a line intersects the \(y\)-axis.
These points have the form \((x,0)\) and \((0,y)\), respectively.
.png?revision=1)
Figure \(\PageIndex{1}\)
To find the \(x\)- and \(y\)-intercepts algebraically, use the fact that all \(x\)-intercepts have a \(y\)-value of zero and all \(y\)-intercepts have an \(x\)-value of zero. To find the \(y\)-intercept, set \(x=0\) and determine the corresponding \(y\)-value. Similarly, to find the \(x\)-intercept, set \(y=0\) and determine the corresponding \(x\)-value.
Find the \(x\)- and \(y\)-intercepts:
\(−3x+2y=12\).
Solution:
To find the \(x\)-intercept, set \(y = 0\).
Therefore, the \(x\)-intercept is \((−4, 0)\). To find the \(y\)-intercept, set \(x = 0\).
\(\begin{aligned} -3x+2y&=12 &\color{Cerulean}{To\:find\:the\:y-intercept,} \\ \color{Cerulean}{\downarrow}\qquad &&\color{Cerulean}{set\:x=0.} \\ -3(\color{OliveGreen}{0}\color{black}{)+2y}&=12 \\ 2y&=12\\y&=6 \end{aligned}\)
Hence the \(y\)-intercept is \((0, 6)\). Note that this linear equation is graphed above.
Answer:
\(x\)-intercept: \((−4, 0)\); \(y\)-intercept: \((0, 6)\)
Find the \(x\)- and \(y\)-intercepts:
\(y=−3x+9\)
Solution:
Begin by finding the \(x\)-intercept.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:y=0.} \\ \color{Cerulean}{\downarrow}&& \\ \color{OliveGreen}{0}&=-3x+9&\color{Cerulean}{Solve\:for\:x.} \\ 3x&=9 \\ x&=3 \end{aligned}\)
The \(x\)-intercept is \((3, 0)\). Next, determine the \(y\)-intercept.
\(\begin{aligned} y&=-3x+9 &\color{Cerulean}{Set\:x=0.}\end{aligned}\)
\( \color{Cerulean}{\downarrow}\qquad\qquad\:\:\:\)
\(\begin{aligned} y&=-3(\color{OliveGreen}{0}\color{black}{)+9} & \color{Cerulean}{Solve\:for\:y.} \\ y&=9 \end{aligned}\)
The \(y\)-intercept is \((0, 9)\).
Answer:
\(x\)-intercept: \((3, 0)\); \(y\)-intercept: \((0, 9)\)
Keep in mind that the intercepts are ordered pairs and not numbers. In other words, the \(x\)-intercept is not \(x=2\) but rather \((2, 0)\). In addition, not all graphs necessarily have both intercepts: for example,
.png?revision=1)
Figure \(\PageIndex{2}\)
The horizontal line graphed above has a \(y\)-intercept of \((0, −2)\) and no \(x\)-intercept.
.png?revision=1)
Figure \(\PageIndex{3}\)
The vertical line graphed above has an \(x\)-intercept \((3, 0)\) and no \(y\)-intercept.
Find the \(x\)- and \(y\)-intercepts:
\(4x−y=2\).
- Answer
-
\(x\)-intercept: \((\frac{1}{2}, 0)\); \(y\)-intercept: \((0, −2)\)
Graphing Lines Using Intercepts
Since two points determine a line, we can use the \(x\)- and \(y\)-intercepts to graph linear equations. We have just outlined an easy method for finding intercepts; now we outline the steps for graphing lines using the intercepts.
Graph using intercepts:
\(2x−3y=12\).
Solution:
Step 1: Find the \(x\)- and \(y\)-intercepts.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{To\:find\:the\:x-intercept,\:set\:y=0.}}}&{\underline{\color{Cerulean}{To\:find\:the\:y-intercept,\:set\:x=0.}}}\\{2x-3y=12}&{2x-3y=12}\\{2x-3(\color{OliveGreen}{0}\color{black}{)=12}}&{2(\color{OliveGreen}{0}\color{black}{)-3y=12}}\\{2x=12}&{-3y=12}\\{x=6}&{y=-4}\\{x-intercept:\:(6,0)}&{y-intercept:\:(0,-4)} \end{array}\)
Step 2: Plot the intercepts and draw the line through them. Use a straightedge to create a nice straight line. Add an arrow on either end to indicate that the line continues indefinitely in either direction.
Answer:
.png?revision=1)
Figure \(\PageIndex{4}\)
Graph using intercepts:
\(y=−\frac{1}{5}x+3\).
Solution:
Begin by determining the \(x\)- and \(y\-intercepts.
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-\frac{1}{5}x+3}&{y=-\frac{1}{5}x+3}\\{\color{OliveGreen}{0}\color{black}{=-\frac{1}{5}x+3}}&{y=-\frac{1}{5}(\color{OliveGreen}{0}\color{black}{)+3}}\\{\frac{1}{5}x=3}&{y=3}\\{\color{Cerulean}{5\cdot}\color{black}{\frac{1}{5}x=}\color{Cerulean}{5\cdot}\color{black}{3}}&{y-intercept:\:(0,3)}\\{x=15}&{}\\{x-intercept:\:(15,0)}&{} \end{array}\)
Next, graph the two points and draw a line through them with a straighedge.
Answer:
.png?revision=1)
Figure \(\PageIndex{5}\)
Graph using intercepts:
\(y=−2x\).
Solution:
\(\begin{array}{c|c}{\underline{\color{Cerulean}{x-intercept}}}&{\underline{\color{Cerulean}{y-intercept}}}\\{y=-2x}&{y=-2x}\\{\color{OliveGreen}{0}\color{black}{=-2x}}&{y=-2(\color{OliveGreen}{0}\color{black}{)}}\\{\frac{0}{\color{Cerulean}{-2}}=\frac{-2x}{\color{Cerulean}{-2}}}&{y=0}\\{0=x}&{y-intercept:\:(0,0)}\\{x-intercept:\:(0,0)}&{}\end{array}\)
Here the \(x\)- and \(y\)-intercepts are actually the same point, the origin. We will need at least one more point so that we can graph the line. Choose any value for \(x\) and determine the corresponding value for \(y\).
.png?revision=1)
Figure \(\PageIndex{6}\)
Use the ordered pair solutions \((0, 0), (−1, 2)\), and \((1, −2)\) to graph the line.
Answer:
.png?revision=1)
Figure \(\PageIndex{7}\)
To summarize, any linear equation can be graphed by finding two points and connecting them with a line drawn with a straightedge. Two important and useful points are the \(x\)- and \(y\)-intercepts; find these points by substituting \(y = 0\) and \(x = 0\), respectively. This method for finding intercepts will be used throughout our study of algebra.
Graph using intercepts:
\(3x−5y=15\).
- Answer
-
\(x\)-intercept: \((5, 0)\); \(y\)-intercept: \((0, −3)\)
Finding Intercepts Given the Graph
The \(x\)- and \(y\)-intercepts are important points on any graph. This chapter will focus on the graphs of linear equations. However, at this point, we can use these ideas to determine intercepts of nonlinear graphs. Remember that intercepts are ordered pairs that indicate where the graph intersects the axes.
Find the \(x\)- and \(y\)-intercepts given the following graph:
.png?revision=1)
Figure \(\PageIndex{8}\)
Solution:
We see that the graph intersects the \(x\)-axis in two places. This graph has two \(x\)-intercepts, namely, \((−4, 0)\) and \((2, 0)\). Furthermore, the graph intersects the \(y\)-axis in one place. The only \(y\)-intercept is \((0, −3)\).
Answer:
\(x\)-intercepts: \((−4, 0), (2, 0)\); \(y\)-intercept: \((0, −3)\)
In our study of algebra, we will see that some graphs have many intercepts. Also, we will see that some graphs do not have any.
Given the following graph, find the \(x\)- and \(y\)-intercepts:
.png?revision=1)
Figure \(\PageIndex{9}\)
Solution:
This is a graph of a circle; we can see that it does not intersect either axis. Therefore, this graph does not have any intercepts.
Answer:
None
Key Takeaways
- Since two points determine any line, we can graph lines using the \(x\)- and \(y\)-intercepts.
- To find the \(x\)-intercept, set \(y = 0\) and solve for \(x\).
- To find the \(y\)-intercept, set \(x = 0\) and solve for \(y\).
- This method of finding \(x\)- and \(y\)-intercepts will be used throughout our study of algebra because it works for any equation.
- To graph a line, find the intercepts, if they exist, and draw a straight line through them. Use a straightedge to create the line and include arrows on either end to indicate that the line extends infinitely in either direction.
- Horizontal and vertical lines do not always have both \(x\)- and \(y\)-intercepts.
Given the graph, find the \(x\)- and \(y\)-intercepts.
1.
.png?revision=1)
Figure \(\PageIndex{10}\)
2.
.png?revision=1)
Figure \(\PageIndex{11}\)
3.
.png?revision=1)
Figure \(\PageIndex{12}\)
4.
.png?revision=1)
Figure \(\PageIndex{13}\)
5.
.png?revision=1)
Figure \(\PageIndex{14}\)
6.
.png?revision=1)
Figure \(\PageIndex{15}\)
- Answer
-
1. \(y\)-intercept: \((0, −3)\); \(x\)-intercept: \((4, 0)\)
3. \(y\)-intercept: \((0, −3)\); \(x\)-intercept: none
5. \(y\)-intercept: \((0, 0)\); \(x\)-intercept: \((0, 0)\)
Find the \(x\)- and \(y\)-intercepts.
- \(5x−4y=20 \)
- \(−2x+7y=−28 \)
- \(x−y=3 \)
- \(−x+y=0 \)
- \(3x−4y=1 \)
- \(−2x+5y=3 \)
- \(\frac{1}{4}x−\frac{1}{3}y=1\)
- \(−\frac{2}{5}x+\frac{3}{4}y=2\)
- \(y=6\)
- \(y=−3\)
- \(x=2\)
- \(x=−1\)
- \(y=mx+b \)
- \(ax+by=c\)
- Answer
-
1. \(x\)-intercept: \((4, 0)\); \(y\)-intercept: \((0, −5) \)
3. \(x\)-intercept: \((3, 0)\); \(y\)-intercept: \((0, −3) \)
5. \(x\)-intercept: \((\frac{1}{3}, 0)\); \(y\)-intercept: \((0, −\frac{1}{4})\)
7. \(x\)-intercept: \((4, 0)\); \(y\)-intercept: \((0, −3) \)
9. \(x\)-intercept: none; \(y\)-intercept: \((0, 6) \)
11. \(x\)-intercept: \((2, 0)\); \(y\)-intercept: none
13. \(x\)-intercept: \((−\frac{b}{m}, 0)\); \(y\)-intercept: \((0, b)\)
Find the intercepts and graph them.
- \(3x+4y=12\)
- \(−2x+3y=6\)
- \(5x−2y=10\)
- \(−4x−8y=16\)
- \(−\frac{1}{2}x+\frac{1}{3}y=1\)
- \(\frac{3}{4}x−\frac{1}{2}y=−3\)
- \(2x−\frac{5}{2}y=10\)
- \(2x−\frac{7}{3}y=−14\)
- \(4x−y=−8\)
- \(6x−y=6\)
- \(–x+2y=1\)
- \(3x+4y=6\)
- \(2x+y=−1\)
- \(−2x+6y=3\)
- \(15x+4y=−60\)
- \(−25x+3y=75\)
- \(4x+2y=0\)
- \(3x−y=0\)
- \(−12x+6y=−4\)
- \(3x+12y=−4\)
- \(y=2x+4\)
- \(y=−x+3\)
- \(y=\frac{1}{2}x+1\)
- \(y=\frac{2}{3}x−3\)
- \(y=−\frac{2}{5}x+1\)
- \(y=−\frac{5}{8}x−\frac{5}{4}\)
- \(y=−\frac{7}{8}x−\frac{7}{2}\)
- \(y=−x+\frac{3}{2}\)
- \(y=3\)
- \(y=\frac{3}{2}\)
- \(x=5\)
- \(x=−2\)
- \(y=5x\)
- \(y=−x\)
- Answer
-
1.
.png?revision=1)
Figure \(\PageIndex{16}\)
3.
.png?revision=1)
Figure \(\PageIndex{17}\)
5.
.png?revision=1)
Figure \(\PageIndex{18}\)
7.
.png?revision=1)
Figure \(\PageIndex{19}\)
9.
.png?revision=1)
Figure \(\PageIndex{20}\)
11.
.png?revision=1)
Figure \(\PageIndex{21}\)
13.
.png?revision=1)
Figure \(\PageIndex{22}\)
15.
.png?revision=1)
Figure \(\PageIndex{23}\)
17.
.png?revision=1)
Figure \(\PageIndex{24}\)
19.
.png?revision=1)
Figure \(\PageIndex{25}\)
21.
.png?revision=1)
Figure \(\PageIndex{26}\)
23.
.png?revision=1)
Figure \(\PageIndex{27}\)
25.
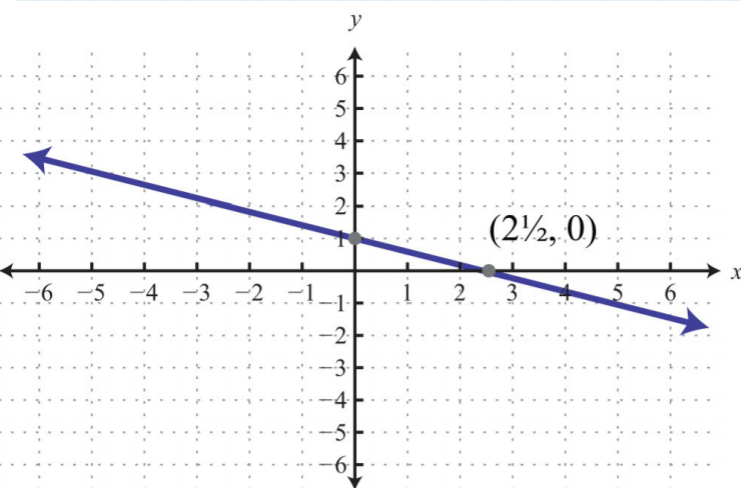.png?revision=1)
Figure \(\PageIndex{28}\)
27.
.png?revision=1)
Figure \(\PageIndex{29}\)
29.
.png?revision=1)
Figure \(\PageIndex{30}\)
31.
.png?revision=1)
Figure \(\PageIndex{31}\)
33.
.png?revision=1)
Figure \(\PageIndex{32}\)
Given the graph find the \(x\)- and \(y\)-intercepts.
1.
.png?revision=1)
Figure \(\PageIndex{33}\)
2.
.png?revision=1)
Figure \(\PageIndex{34}\)
3.
.png?revision=1)
Figure \(\PageIndex{35}\)
4.
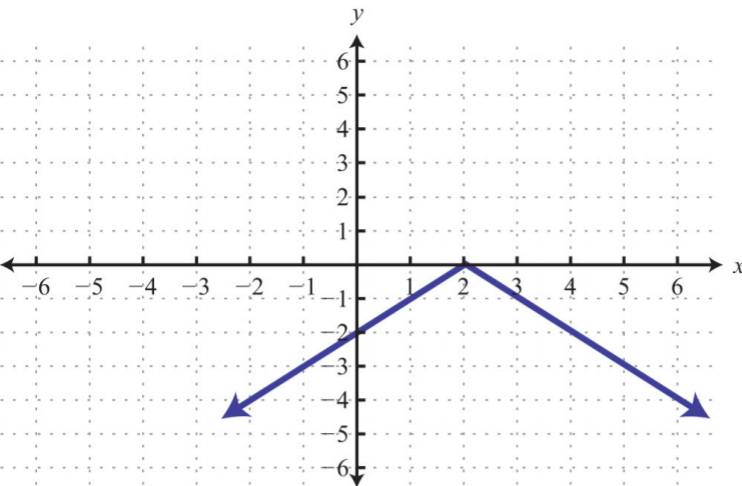.png?revision=1)
Figure \(\PageIndex{36}\)
5.
.png?revision=1)
Figure \(\PageIndex{37}\)
6.
.png?revision=1)
Figure \(\PageIndex{38}\)
7.
.png?revision=1)
Figure \(\PageIndex{39}\)
8.
.png?revision=1)
Figure \(\PageIndex{40}\)
9.
.png?revision=1)
Figure \(\PageIndex{41}\)
10.
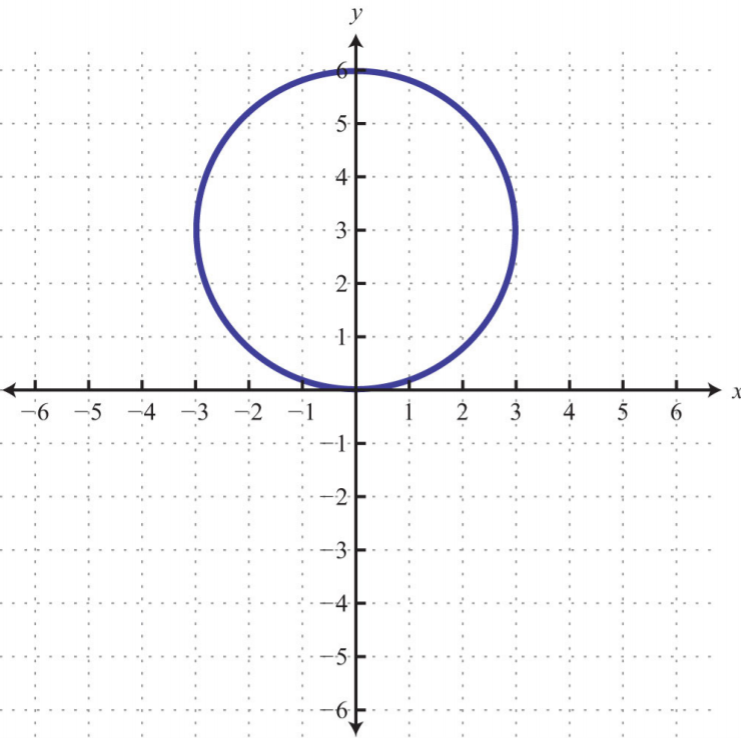.png?revision=1)
Figure \(\PageIndex{42}\)
- Answer
-
1. \(x\)-intercepts: \((−3, 0), (3, 0)\); \(y\)-intercept: \((0, −3)\)
3. \(x\)-intercepts: \((−4, 0), (0, 0)\); \(y\)-intercept: \((0, 0) \)
5. \(x\)-intercepts: \((−2, 0), (2, 0)\); \(y\)-intercept: \((0, −1) \)
7. \(x\)-intercepts: \((−3, 0), (0, 0), (2, 0)\); \(y\)-intercept: \((0, 0) \)
9. \(x\)-intercepts: \((−4, 0), (4, 0)\); \(y\)-intercepts: \((0, −4), (0, 4)\)
- What are the \(x\)-intercepts of the line \(y = 0\)?
- What are the \(y\)-intercepts of the line \(x = 0\)?
- Do all lines have intercepts?
- How many intercepts can a circle have? Draw circles showing all possible numbers of intercepts.
- Research and post the definitions of line segment, ray, and line. Why are the arrows important?
- Answer
-
1. Answers may vary
3. Answers may vary
5. Answers may vary


