3.4: Graph Using the y-Intercept and Slope
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identify and find the slope of a line.
- Graph a line using the slope and
Slope
The steepness of any incline can be measured as the ratio of the vertical change to the horizontal change. For example, a
.png?revision=1)
Figure
In mathematics, we call the incline of a line the slope and use the letter
The rise and the run can be positive or negative. A positive rise corresponds to a vertical change up and a negative rise corresponds to a vertical change down. A positive run denotes a horizontal change to the right and a negative run corresponds to a horizontal change to the left. Given the graph, we can calculate the slope by determining the vertical and horizontal changes between any two points.
Find the slope of the given line:
.png?revision=1)
Figure
Solution:
From the given points on the graph, count
Answer:
Here we have a negative slope, which means that for every
.png?revision=1)
Figure
Reading the graph from left to right, we see that lines with an upward incline have positive slopes and lines with a downward incline have negative slopes.
.png?revision=1)
Figure
If the line is horizontal, then the rise is
The slope of a horizontal line is
The slope of a vertical line is undefined.
Find the slope of the given line:
.png?revision=1)
Figure
- Answer
-
Calculating the slope can be difficult if the graph does not have points with integer coordinates. Therefore, we next develop a formula that allows us to calculate the slope algebraically. Given any two points
.png?revision=1)
Figure
This leads us to the slope formula. Given any two points
Find the slope of the line passing through
Solution:
Given
Answer:
We can graph the line described in the previous example and verify that the slope is
.png?revision=1)
Figure
Certainly the graph is optional; the beauty of the slope formula is that we can obtain the slope, given two points, using only algebra.
Find the slope of the line passing through
Solution:
Answer:
When using the slope formula, take care to be consistent since order does matter. You must subtract the coordinates of the first point from the coordinates of the second point for both the numerator and the denominator in the same order.
Find the slope of the line passing through
Solution:
Answer:
Find the slope of the line passing through
Solution:
Answer:
The slope
Calculate the slope of the line passing through
- Answer
-
When considering the slope as a rate of change it is important to include the correct units.
A Corvette Coupe was purchased new in 1970 for about $
.png?revision=1)
Figure
- Determine the rate at which the car depreciated in value from 1970 to 1985.
- Determine the rate at which the car appreciated in value from 1985 to 2000.
Solution:
Notice that the value depends on the age of the car and that the slope measures the rate in dollars per year.
a. The slope of the line segment depicting the value for the first 15 years is
b. The slope of the line segment depicting the value for the next 15 years is
Answer:
- The value of the car depreciated $
- The value of the car appreciated $
Slope-Intercept Form of a Line
To this point, we have learned how to graph lines by plotting points and by using the
Determine the slope and
Solution:
In this form, the coefficient of
.png?revision=1)
Figure
Answer:
The
It is not always the case that the linear equation is given in slope-intercept form. When it is given in standard form, you have to first solve for
Express
Solution:
Begin by solving for
Answer:
Slope-intercept form:
Once the equation is in slope-intercept form, we immediately have one point to plot, the
slope:
Starting from the point
.png?revision=1)
Figure
It is not necessary to check that the second point, (5, 3), solves the original linear equation. However, we do it here for the sake of completeness.
Marking off the slope in this fashion produces as many ordered pair solutions as we desire. Notice that if we mark off the slope again, from the point
Graph:
Solution:
In this example, we outline the general steps for graphing a line using slope-intercept form.
Step 1: Solve for
Step 2: Identify the
slope:
Step 3: Plot the
.png?revision=1)
Figure
Step 4: Draw the line through the two points with a straightedge.
Answer:
.png?revision=1)
Figure
In this example, we notice that we could get the
We could obtain another point on the line by marking off the equivalent slope down
.png?revision=1)
Figure
Marking off the slope multiple times is not necessarily always going to give us the
Graph and find the
Solution:
The equation is given in slope-intercept form. Therefore, by inspection, we have the
slope:
.png?revision=1)
Figure
We can see that the
Answer:
The
Graph:
Solution:
Begin by solving for
The equation
slope:
Answer:
.png?revision=1)
Figure
Graph
- Answer
-
.png?revision=1)
Figure
Key Takeaways
- Slope measures the steepness of a line as rise over run. A positive rise denotes a vertical change up, and a negative rise denotes a vertical change down. A positive run denotes a horizontal change right, and a negative run denotes a horizontal change left.
- Horizontal lines have a slope of zero, and vertical lines have undefined slopes.
- Given any two points on a line, we can algebraically calculate the slope using the slope formula,
- Any nonvertical line can be written in slope-intercept form,
- If we know the
- We can obtain as many points on the line as we wish by marking off the slope multiple times.
Determine the slope and the
1.
.png?revision=1)
Figure
2.
.png?revision=1)
Figure
3.
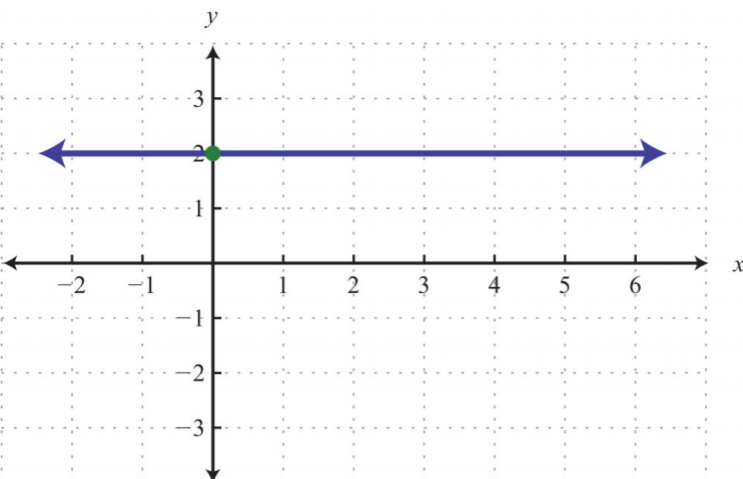.png?revision=1)
Figure
4.
.png?revision=1)
Figure
5.
.png?revision=1)
Figure
6.
.png?revision=1)
Figure
- Answer
-
1.
3.
5.
Determine the slope, given two points.
- A roof drops
- A road drops
- The following graph gives the US population of persons 65 years old and over. At what rate did this population increase from 2000 to 2008?
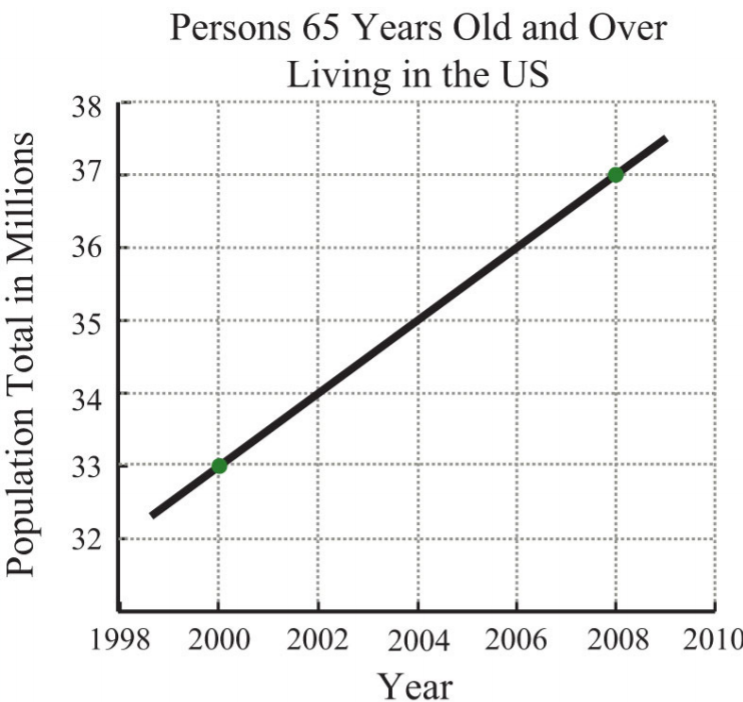.png?revision=1)
Figure
20. The following graph gives total consumer credit outstanding in the United States. At what rate did consumer credit increase from 2002 to 2008?
.png?revision=1)
Figure
21. A commercial van was purchased new for $
22. A commercial-grade copy machine was purchased new for $
23. Find
24. Find
25. Find
26. Find
- Answer
-
1.
3.
5.
7.
9.
11.
13.
15. Undefined
17.
19.
21. $
23.
25.
Express the given linear equation in slope-intercept form and identify the slope and
- Answer
-
1.
3.
5.
7.
Graph the line given the slope and the
- Answer
-
1.
.png?revision=2)
Figure
3.
.png?revision=1)
Figure
5.
.png?revision=1)
Figure
7.
.png?revision=1)
Figure
9.
.png?revision=1)
Figure
Graph using the slope and
- On the same set of axes, graph the three lines, where
- On the same set of axes, graph the three lines, where
- Answer
-
1.
.png?revision=1)
Figure
3.
.png?revision=1)
Figure
5.
.png?revision=1)
Figure
7.
.png?revision=1)
Figure
9.
.png?revision=1)
Figure
11.
.png?revision=1)
Figure
13.
.png?revision=1)
Figure
15.
.png?revision=1)
Figure
17.
.png?revision=1)
Figure
19.
.png?revision=1)
Figure
21.
.png?revision=1)
Figure
23.
.png?revision=1)
Figure
- Name three methods for graphing lines. Discuss the pros and cons of each method.
- Choose a linear equation and graph it three different ways. Scan the work and share it on the discussion board.
- Why do we use the letter m for slope?
- How are equivalent fractions useful when working with slopes?
- Can we graph a line knowing only its slope?
- Research and discuss the alternative notation for slope:
- What strategies for graphing lines should be brought to an exam? Explain
- Answer
-
1. Answers may vary
3. Answers may vary
5. Answers may vary
7. Answers may vary


