3.E: Review Exercises and Sample Exam
- Page ID
- 24126
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Review Exercises
Graph the given set of ordered pairs.
- \(\{(−3, 4), (−4, 0), (0, 3), (2, 4)\}\)
- \(\{(−5, 5), (−3, −1), (0, 0), (3, 2)\}\)
- Graph the points \((−3, 5), (−3, −3),\) and \((3, −3)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Graph the points \((−4, 1), (0, 1), (0, −2),\) and \((−4, −2)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Graph the points \((1, 0), (4, 0), (1, −5),\) and \((4, −5)\) on a rectangular coordinate plane. Connect the points and calculate the perimeter of the shape.
- Graph the points \((−5, 2), (−5, −3), (1, 2),\) and \((1, −3)\) on a rectangular coordinate plane. Connect the points and calculate the perimeter of the shape.
- Answer
-
1.
.png?revision=1)
Figure 3.E.1
3. Area: \(24\) square units
.png?revision=1)
Figure 3.E.2
5. Perimeter: \(16\) units
.png?revision=1)
Figure 3.E.3
Calculate the distance between the given two points.
- \((−1, −2)\) and \((5, 6)\)
- \((2, −5)\) and \((−2, −2)\)
- \((−9, −3)\) and \((−8, 4)\)
- \((−1, 3)\) and \((1, −3)\)
- Answer
-
1. \(10\) units
3. \(5\sqrt{2}\) units
Calculate the midpoint between the given points.
- \((−1, 3)\) and \((5, −7)\)
- \((6, −3)\) and \((−8, −11)\)
- \((7, −2)\) and \((−6, −1)\)
- \((−6, 0)\) and \((0, 0)\)
- Show algebraically that the points \((−1, −1), (1, −3),\) and \((2, 0)\) form an isosceles triangle.
- Show algebraically that the points \((2, −1), (6, 1),\) and \((5, 3)\) form a right triangle.
- Answer
-
1. \((2,-2)\)
3. \((\frac{1}{2},-\frac{3}{2})\)
5. Answers may vary
Determine whether the given point is a solution.
- \(−5x+2y=7\); \((1, −1)\)
- \(6x−5y=4\); \((−1, −2)\)
- \(y=\frac{3}{4}x+1\); \((−\frac{2}{3}, \frac{1}{2})\)
- \(y=−\frac{3}{5}x−2\); \((10, −8)\)
- Answer
-
1. No
3. Yes
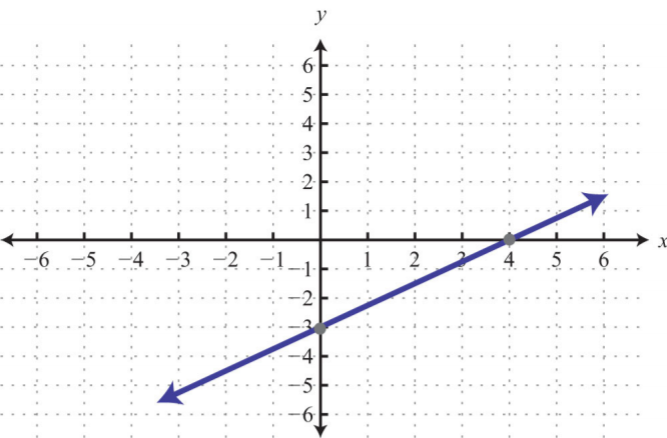
Find at least five ordered pair solutions and graph.
- \(y=−x+2\)
- \(y=2x−3\)
- \(y=\frac{1}{2}x−2\)
- \(y=−\frac{2}{3}x\)
- \(y=3\)
- \(x=−3\)
- \(x−5y=15\)
- \(2x−3y=12\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.4
3.
.png?revision=1)
Figure 3.E.5
5.
.png?revision=1)
Figure 3.E.6
7.
.png?revision=1)
Figure 3.E.7
Given the graph, find the \(x\)- and \(y\)- intercepts.
1.
.png?revision=1)
Figure 3.E.8
2.
.png?revision=1)
Figure 3.E.9
3.
.png?revision=1)
Figure 3.E.10
4.
.png?revision=1)
Figure 3.E.11
- Answer
-
1. \(y\)-intercept: \((0, −2)\); \(x\)-intercept: \((−4, 0)\)
3. \(y\)-intercept: none; \(x\)-intercept: \((5, 0)\)
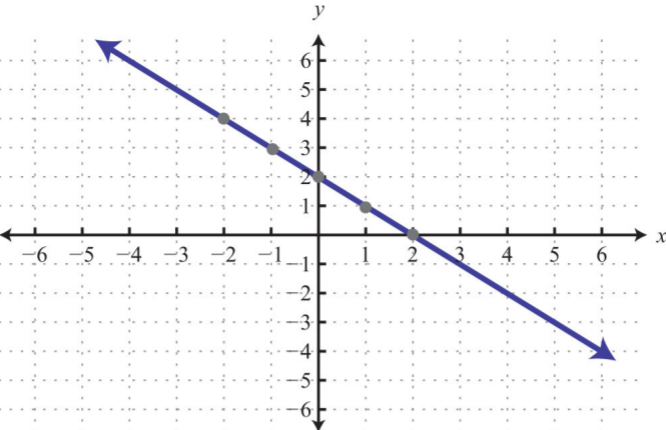
Find the intercepts and graph them.
- \(3x−4y=12\)
- \(2x−y=−4\)
- \(\frac{1}{2}x−\frac{1}{3}y=1\)
- \(−\frac{1}{2}x+\frac{2}{3}y=2\)
- \(y=−\frac{5}{3}x+5\)
- \(y=−3x+4\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.12
3.
.png?revision=1)
Figure 3.E.13
5.
.png?revision=1)
Figure 3.E.14
Given the graph, determine the slope and \(y\)-intercept.
1.
.png?revision=1)
Figure 3.E.15
2.
.png?revision=1)
Figure 3.E.16
- Answer
-
1. \(y\)-intercept: \((0, 1)\); slope: \(−2\)
Determine the slope, given two points.
- \((−3, 8)\) and \((5, −6)\)
- \((0, −5)\) and \((−6, 3)\)
- \((\frac{1}{2}, −\frac{2}{3})\) and \((\frac{1}{4}, −\frac{1}{3})\)
- \((5, −\frac{3}{4})\) and \((2, −\frac{3}{4})\)
- Answer
-
1. \(-\frac{7}{4}\)
3. \(-\frac{4}{3}\)
Express in slope-intercept form and identify the slope and \(y\)-intercept.
- \(12x−4y=8\)
- \(3x−6y=24\)
- \(−\frac{1}{3}x+\frac{3}{4}y=1\)
- \(−5x+3y=0\)
- Answer
-
1. \(y=3x−2\); slope: \(3\); \(y\)-intercept \((0, −2)\)
3. \(y=\frac{4}{9}x+\frac{4}{3}\); slope: \(\frac{4}{9}\); \(y\)-intercept \((0, \frac{4}{3})\)
- \(y=−x+3\)
- \(y=4x−1\)
- \(y=−2x\)
- \(y=−\frac{5}{2}x+3\)
- \(2x−3y=9\)
- \(2x+\frac{3}{2}y=3\)
- \(y=0\)
- \(x−4y=0\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.17
3.
.png?revision=1)
Figure 3.E.18
5.
.png?revision=1)
Figure 3.E.19
7.
.png?revision=1)
Figure 3.E.20
Given the graph, determine the equation of the line.
1.
.png?revision=1)
Figure 3.E.21
2.
.png?revision=1)
Figure 3.E.22
3.
.png?revision=1)
Figure 3.E.23
4.
.png?revision=1)
Figure 3.E.24
- Answer
-
1. \(y=−2x+1\)
3. \(y=−5\)
Find the equation of a line, given the slope and a point on the line.
- \(m = \frac{1}{2}\); \((−4, 8)\)
- \(m = −\frac{1}{5}\); \((−5, −9)\)
- \(m = \frac{2}{3}\); \((1, −2)\)
- \(m = −\frac{3}{4}\); \((2, −3)\)
- Answer
-
1. \(y=\frac{1}{2}x+10\)
3. \(y=\frac{2}{3}x−\frac{8}{3}\)
Find the equation of the line given two points on the line.
- \((−5, −5)\) and \((10, 7)\)
- \((−6, 12)\) and \((3, −3)\)
- \((2, −1)\) and \((−2, 2)\)
- \((\frac{5}{2}, −2)\) and \((−5, \frac{5}{2})\)
- \((7, −6)\) and \((3, −6)\)
- \((10, 1)\) and \((10, −3)\)
- Answer
-
1. \(y=\frac{4}{5}x−1\)
3. \(y=−\frac{3}{4}x+\frac{1}{2}\)
5. \(y=−6\)
Determine if the lines are parallel, perpendicular, or neither.
- \(\left\{\begin{aligned}−3x+7y&=14\\6x−14y&=42\end{aligned}\right.\)
- \(\left\{\begin{aligned}2x+3y&=18\\2x−3y&=36\end{aligned}\right.\)
- \(\left\{\begin{aligned}x+4y&=2\\8x−2y=&−1\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=2\\x&=2\end{aligned}\right.\)
- Answer
-
1. Parallel
3. Perpendicular
Find the equation of the line in slope-intercept form.
- Parallel to \(5x−y=15\) and passing through \((−10, −1)\).
- Parallel to \(x−3y=1\) and passing through \((2, −2)\).
- Perpendicular to \(8x−6y=4\) and passing through \((8, −1)\).
- Perpendicular to \(7x+y=14\) and passing through \((5, 1)\).
- Parallel to \(y=1\) and passing through \((4, −1)\).
- Perpendicular to \(y=1\) and passing through \((4, −1)\).
- Answer
-
1. \(y=5x+49\)
3. \(y=−\frac{3}{4}x+5\)
5. \(y=−1\)
Determine the domain and range and state whether it is a function or not.
1. \(\{(−10, −1), (−5, 2), (5, 2)\}\)
2. \(\{(−12, 4), (−1, −3), (−1, −2)\}\)
3.
.png?revision=1)
Figure 3.E.25
4.
.png?revision=1)
Figure 3.E.26
5.
.png?revision=1)
Figure 3.E.27
6.
.png?revision=1)
Figure 3.E.28
- Answer
-
1. Domain: \(\{−10, −5, 5\}\); range: \(\{−1, 2\}\); function: yes
3. Domain: \(R\); range: \(R\); function: yes
5. Domain: \([−3,∞)\); range: \(R\); function: no
Given the following,
- \(f(x)=9x−4\), find \(f(−1)\).
- \(f(x)=−5x+1\), find \(f(−3)\).
- \(g(x)=\frac{1}{2}x−\frac{1}{3}\), find \(g(−\frac{1}{3})\).
- \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), find \(g(\frac{2}{3})\).
- \(f(x)=9x−4\), find \(x\) when \(f(x)=0\).
- \(f(x)=−5x+1\), find \(x\) when \(f(x)=2\).
- \(g(x)=\frac{1}{2}x−\frac{1}{3}\), find \(x\) when \(g(x)=1\).
- \(g(x)=−\frac{3}{4}x+\frac{1}{3}\), find \(x\) when \(g(x)=−1\).
- Answer
-
1. \(f(−1)=−13\)
3. \(g(−\frac{1}{3})=−\frac{1}{2}\)
5. \(x=\frac{4}{9}\)
7. \(x=\frac{8}{3}\)
Given the graph of a function \(f(x)\), determine the following.
.png?revision=1)
Figure 3.E.29
- \(f(3)\)
- \(x\) when \(f(x)=4\)
- Answer
-
1. \(f(3)=−2\)
Is the ordered pair a solution to the given inequality?
- \(6x−2y≤1\); \((−3, −7)\)
- \(−3x+y>2\); \((0, 2)\)
- \(6x−10y<-1\); \((5,-3)\)
- \(x-\frac{1}{3}y>0\); \((1, 4)\)
- \(y>0\); \((−3, −1)\)
- \(x≤−5\); \((−6, 4)\)
- Answer
-
1. Yes
3. No
5. Yes
Graph the solution set.
- \(y≥−2x+1\)
- \(y<3x−4\)
- \(−x+y≤3\)
- \(\frac{5}{2}x+\frac{1}{2}y≤2\)
- \(3x−5y>0\)
- \(y>0\)
- Answer
-
1.
.png?revision=1)
Figure 3.E.30
3.
.png?revision=1)
Figure 3.E.31
5.
.png?revision=1)
Figure 3.E.32
Sample Exam
- Graph the points \((−4, −2), (−4, 1),\) and \((0, −2)\) on a rectangular coordinate plane. Connect the points and calculate the area of the shape.
- Is \((−2, 4)\) a solution to \(3x−4y=−10\)? Justify your answer.
- Answer
-
1. Area: \(6\) square units
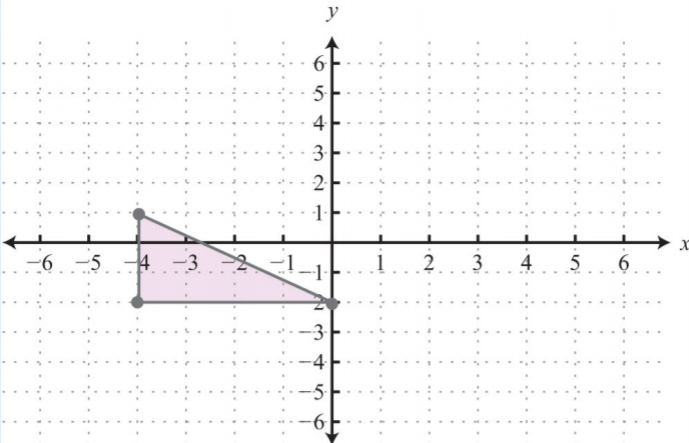.png?revision=1)
Figure 3.E.33
Given the set of \(x\)-values \(\{−2, −1, 0, 1, 2\}\), find the corresponding \(y\)-values and graph the following.
- \(y=x−1\)
- \(y=−x+1\)
- On the same set of axes, graph \(y=4\) and \(x=−3\). Give the point where they intersect.
- Answer
-
1.
.png?revision=1)
Figure 3.E.34
3. Intersection: \((-3,4)\)
.png?revision=1)
Figure 3.E.35
Find the \(x\)- and \(y\)-intercepts and use those points to graph the following.
- \(2x−y=8\)
- \(12x+5y=15\)
- Calculate the slope of the line passing through \((−4, −5)\) and \((−3, 1)\).
- Answer
-
2.
.png?revision=1)
Figure 3.E.36
Determine the slope and \(y\)-intercept. Use them to graph the following.
- \(y=−\frac{3}{2}x+6\)
- \(5x−2y=6\)
- Given \(m=−3\), determine \(m_{⊥}\).
- Are the given lines parallel, perpendicular, or neither? \(\left\{\begin{aligned} -2x+3y&=-12\\4x-6y&=30 \end{aligned}\right.\)
- Determine the slope of the given lines.
- \(y=−2\)
- \(x=\frac{1}{3}\)
- Are these lines parallel, perpendicular, or neither?
- Determine the equation of the line with slope \(m=−\frac{3}{4}\) passing through \((8, 1)\).
- Find the equation to the line passing through \((−2, 3)\) and \((4, 1)\).
- Find the equation of the line parallel to \(5x−y=6\) passing through \((−1, −2)\).
- Find the equation of the line perpendicular to \(−x+2y=4\) passing through \((\frac{1}{2}, 5)\).
- Answer
-
1. Slope: \(−\frac{3}{2}\); \(y\)-intercept: \((0, 6)\)
.png?revision=1)
Figure 3.E.37
3. \(m_{⊥}=\frac{1}{3}\)
5. a. \(0\); b. Undefined; c. Perpendicular
6. \(y=−\frac{3}{4}x+7\)
8. \(y=5x+3\)
Given a linear function \(f(x)=−\frac{4}{5}x+2\), determine the following.
- \(f(10)\)
- \(x\) when \(f(x)=0\)
- Graph the solution set: \(3x−4y>4\).
- Graph the solution set: \(y−2x≥0\).
- A rental car company charges $\(32.00\) plus $\(0.52\) per mile driven. Write an equation that gives the cost of renting the car in terms of the number of miles driven. Use the formula to determine the cost of renting the car and driving it \(46\) miles.
- A car was purchased new for $\(12,000\) and was sold 5 years later for $\(7,000\). Write a linear equation that gives the value of the car in terms of its age in years.
- The area of a rectangle is \(72\) square meters. If the width measures \(4\) meters, then determine the length of the rectangle.
- Answer
-
1. \(f(10)=−6\)
3.
.png?revision=1)
Figure 3.E.38
5. cost\(=0.52x+32\); $\(55.92\)
7. \(18\) meters