2.8: Solve Absolute Value Inequalities
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Solve absolute value equations
- Solve absolute value inequalities with “less than”
- Solve absolute value inequalities with “greater than”
- Solve applications with absolute value
Before you get started, take this readiness quiz.
Solve Absolute Value Equations
As we prepare to solve absolute value equations, we review our definition of absolute value.
The absolute value of a number is its distance from zero on the number line.
The absolute value of a number n is written as
Absolute values are always greater than or equal to zero.
We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:
Figure
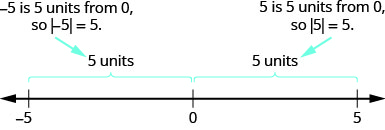
For the equation |x|=5,|x|=5, we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and −5−5 are five units from zero on the number line. They are the solutions to the equation.
The solution can be simplified to a single statement by writing
We can generalize this to the following property for absolute value equations.
For any algebraic expression, u, and any positive real number, a,
Remember that an absolute value cannot be a negative number.
Solve:
- Solution a
-
- Solution b
-
Since an absolute value is always positive, there are no solutions to this equation. - Solution c
-
Both equations tell us that z=0z=0 and so there is only one solution.
Solve:
- Answer a
-
- Answer b
-
no solution
- Answer c
-
0
Solve:
- Answer a
-
- Answer b
-
no solution
- Answer c
-
0
To solve an absolute value equation, we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.
How to Solve Absolute Value Equations
Solve
- Solution
-




Solve:
- Answer
-
Solve:
- Answer
-
The steps for solving an absolute value equation are summarized here.
- Isolate the absolute value expression.
- Write the equivalent equations.
- Solve each equation.
- Check each solution.
Solve
- Solution
-
Isolate the absolute value expression. Write the equivalent equations. Solve each equation. Check:
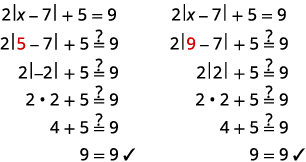
Solve:
- Answer
-
Solve:
- Answer
-
Remember, an absolute value is always positive!
Solve:
- Solution
-
Solve:
- Answer
-
No solution
Solve:
- Answer
-
No solution
Some of our absolute value equations could be of the form
How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, u, and a positive real number, a, if
This tell us that
This leads us to the following property for equations with two absolute values.
For any algebraic expressions, u and v,
When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.
Solve:
- Solution
-
Solve:
- Answer
-
Solve:
- Answer
-
Solve Absolute Value Inequalities with “Less Than”
Let’s look now at what happens when we have an absolute value inequality. Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work. Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation
What about the inequality
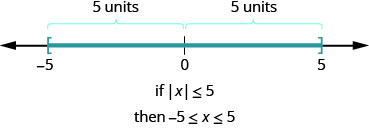
In a more general way, we can see that if
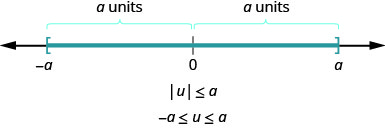
This result is summarized here.
For any algebraic expression, u, and any positive real number, a,
After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.
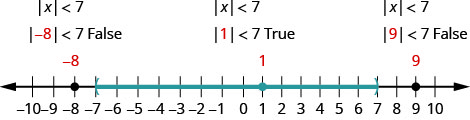
Solve
- Solution
-
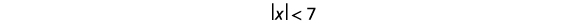
Write the equivalent inequality. 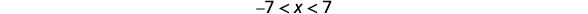
Graph the solution. 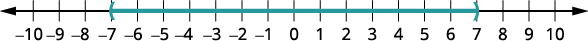
Write the solution using interval notation. 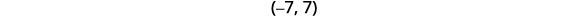
Check:
To verify, check a value in each section of the number line showing the solution. Choose numbers such as −8,−8, 1, and 9.
Graph the solution and write the solution in interval notation:
- Answer
-
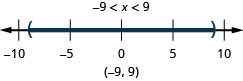
Graph the solution and write the solution in interval notation:
- Answer
-
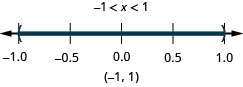
Solve
- Solution
-
Step 1. Isolate the absolute value expression.
It is isolated.Step 2. Write the equivalent compound inequality. Step 3. Solve the compound inequality.
Step 4. Graph the solution. 
Step 5. Write the solution using interval notation. Check:
The check is left to you.
Solve
- Answer
-
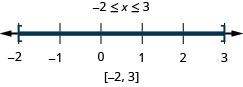
Solve
- Answer
-
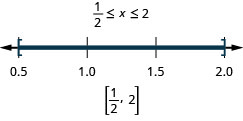
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Absolute Value Inequalities with “Greater Than”
What happens for absolute value inequalities that have “greater than”? Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.
We started with the inequality
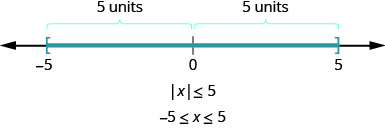
Now we want to look at the inequality
Again both
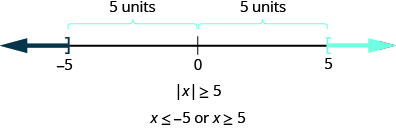
In a more general way, we can see that if
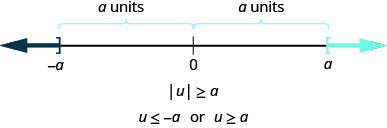
This result is summarized here.
For any algebraic expression, u, and any positive real number, a,
Solve
- Solution
-
Write the equivalent inequality. Graph the solution. 
Write the solution using interval notation. Check: To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6,−6, 0, and 7.
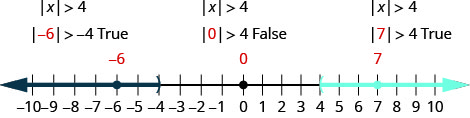
Solve
- Answer
-
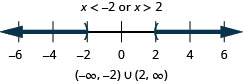
Solve
- Answer
-
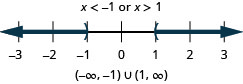
Solve
- Solution
-
Step 1. Isolate the absolute value expression. It is isolated. Step 2. Write the equivalent compound inequality. Step 3. Solve the compound inequality.
Step 4. Graph the solution. 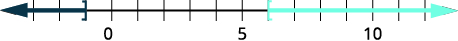
Step 5. Write the solution using interval notation. Check:
The check is left to you.
Solve
- Answer
-
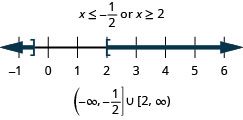
Solve
- Answer
-
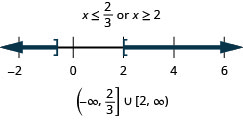
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Applications with Absolute Value
Absolute value inequalities are often used in the manufacturing process. An item must be made with near perfect specifications. Usually there is a certain tolerance of the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.
The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by
- Solution
-
The ideal diameter of a rod needed for a machine is 80 mm. The actual diameter can vary from the ideal diameter by 0.009 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
The diameter of the rod can be between 79.991 and 80.009 mm.
The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
The diameter of the rod can be between 74.95 and 75.05 mm.
Access this online resource for additional instruction and practice with solving linear absolute value equations and inequalities.
- Solving Linear Absolute Value Equations and Inequalities
Key Concepts
- Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as
Absolute values are always greater than or equal to zero. - Absolute Value Equations
For any algebraic expression, u, and any positive real number, a,
Remember that an absolute value cannot be a negative number. - How to Solve Absolute Value Equations
- Isolate the absolute value expression.
- Write the equivalent equations.
- Solve each equation.
- Check each solution.
- Equations with Two Absolute Values
For any algebraic expressions, u and v,
- Absolute Value Inequalities with
For any algebraic expression, u, and any positive real number, a,
- How To Solve Absolute Value Inequalities with
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation
- Absolute Value Inequalities with
For any algebraic expression, u, and any positive real number, a,
- How To Solve Absolute Value Inequalities with
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation


