2.8E: Exercises

Last updated
Save as PDF

Page ID: 30300

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Solve Absolute Value Equations

In the following exercises, solve.

1. a. $|x|=6$ b. $|y|=−3$ c. $|z|=0$

2. a. $ |x|=4$ b. $|y|=−5$ c. $|z|=0$

Answer: a. $x=4,x=−4$ b. no solution c. $z=0$

3. a. $|x|=7$ b. $|y|=−11$ c. $|z|=0$

4. a. $|x|=3$ b. $|y|=−1$ c. $|z|=0$

Answer: a. $x=3,x=−3$ b. no solution c. $z=0$

5. $|2x−3|−4=1$

6. $|4x−1|−3=0$

Answer: $x=1, \,x=−\frac{1}{2}$

7. $|3x−4|+5=7$

8. $|4x+7|+2=5$

Answer: $x=−1, \,x=−\frac{5}{2}$

9. $4|x−1|+2=10$

10. $3|x−4|+2=11$

Answer: $x=7, \,x=1$

11. $3|4x−5|−4=11$

12. $3|x+2|−5=4$

Answer: $x=1, \,x=−5$

13. $−2|x−3|+8=−4$

14. $−3|x−4|+4=−5$

Answer: $x=7, \,x=1$

15. $|34x−3|+7=2$

16. $|35x−2|+5=2$

Answer: no solution

17. $|12x+5|+4=1$

18. $|14x+3|+3=1$

Answer: no solution

19. $|3x−2|=|2x−3|$

20. $|4x+3|=|2x+1|$

Answer: $x=−1, \,x=−\frac{2}{3}$

21. $|6x−5|=|2x+3|$

22. $|6−x|=|3−2x|$

Answer: $x=−3, \,x=3$

Solve Absolute Value Inequalities with “less than”

In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.

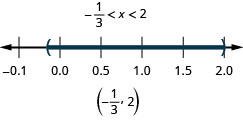
23. $|x|<5$

24. $|x|<1$

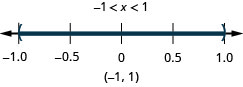
Answer: $The solution is negative 1 is less than x which is less than 1. The number line shows an open circle at negative 1, an open circle at 1, and shading between the circles. The interval notation is negative 1 to 1 within parentheses.$

25. $|x|\leq 8$

26. $|x|\leq 3$

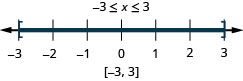
Answer: $The solution is negative 3 is less than or equal to x which is less than or equal to 3. The number line shows a closed circle at negative 3, a closed circle at 3, and shading between the circles. The interval notation is negative 3 to 3 within brackets.$

27. $|3x−3|\leq 6$

28. $|2x−5|\leq 3$

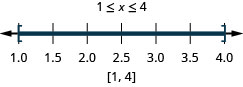
Answer: $The solution is 1 is less than or equal to x which is less than or equal to 4. The number line shows a closed circle at 1, a closed circle at 4, and shading between the circles. The interval notation is 1 to 4 within brackets.$

29. $|2x+3|+5<4$

30. $|3x−7|+3<1$

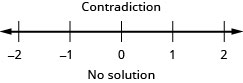
Answer: $The solution is a contradiction. So, there is no solution. As a result, there is no graph or the number line or interval notation.$

31. $|4x−3|<1$

32. $|6x−5|<7$

Answer: $The solution is negative one-third is less than x which is less than 2. The number line shows an open circle at negative one-half, an open circle at 2, and shading between the circles. The interval notation is negative one-third to 2 within parentheses.$

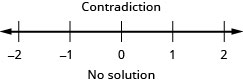
33. $|x−4|\leq −1$

34. $|5x+1|\leq −2$

Answer: $The solution is a contradiction. So, there is no solution. As a result, there is no graph or the number line or interval notation.$

Solve Absolute Value Inequalities with “greater than”

In the following exercises, solve each inequality. Graph the solution and write the solution in interval notation.

35. $|x|>3$

36. $|x|>6$

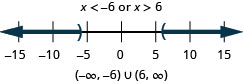
Answer: $The solution is x is less than negative 6 or x is greater than 6. The number line shows an open circle at negative 6 with shading to its left and an open circle at 6 with shading to its right. The interval notation is the union of negative infinity to negative 6 within parentheses and 6 to infinity within parentheses$

37. $|x|\geq 2$

38. $|x|\geq 5$

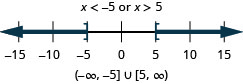
Answer: $The solution is x is less than negative 5 or x is greater than 5. The number line shows an open circle at negative 5 with shading to its left and an open circle at 5 with shading to its right. The interval notation is the union of negative infinity to negative 5 within parentheses and 5 to infinity within parentheses.$

39. $|3x−8|>−1$

40. $|x−5|>−2$

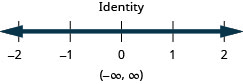
Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

41. $|3x−2|>4$

42. $|2x−1|>5$

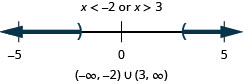
Answer: $The solution is x is less than negative 2 or x is greater than 3. The number line shows an open circle at negative 2 with shading to its left and an open circle at 3 with shading to its right. The interval notation is the union of negative infinity to negative 2 within parentheses and 3 to infinity within parentheses.$

43. $|x+3|\geq 5$

44. $|x−7|\geq 1$

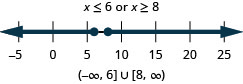
Answer: $The solution is x is less than or equal to 6 or x is greater than or equal to 8. The number line shows a closed circle at 6 with shading to its left and a closed circle at 8 with shading to its right. The interval notation is the union of negative infinity to 6 within parenthesis and a bracket and 8 to infinity within a bracket and a parenthesis.$

45. $3|x|+4\geq 1$

46. $5|x|+6\geq 1$

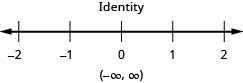
Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

In the following exercises, solve. For each inequality, also graph the solution and write the solution in interval notation.

47. $2|x+6|+4=8$

48. $|3x−4|\geq 2$

Answer: $x=4,x=27$

49. $|6x−5|=|2x+3|$

50. $|4x−3|<5$

Answer: $x=3,x=2$

51. $|2x−5|+2=3$

52. $|3x+1|−3=7$

Answer: $x=3,x=−\frac{11}{3}$

53. $|7x+2|+8<4$

54. $5|2x−1|−3=7$

Answer: $x=\frac{3}{2},x=−\frac{1}{2}$

55. $|x−7|>−3$

56. $|8−x|=|4−3x|$

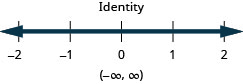
Answer: $The solution is an identity. Its solution on the number line is shaded for all values. The solution in interval notation is negative infinity to infinity within parentheses.$

Solve Applications with Absolute Value

In the following exercises, solve.

57. A chicken farm ideally produces 200,000 eggs per day. But this total can vary by as much as 25,000 eggs. What is the maximum and minimum expected production at the farm?

58. An organic juice bottler ideally produces 215,000 bottle per day. But this total can vary by as much as 7,500 bottles. What is the maximum and minimum expected production at the bottling company?

Answer: The minimum to maximum expected production is 207,500 to 2,225,000 bottles

59. In order to insure compliance with the law, Miguel routinely overshoots the weight of his tortillas by 0.5 gram. He just received a report that told him that he could be losing as much as $100,000 per year using this practice. He now plans to buy new equipment that guarantees the thickness of the tortilla within 0.005 inches. If the ideal thickness of the tortilla is 0.04 inches, what thickness of tortillas will be guaranteed?

60. At Lilly’s Bakery, the ideal weight of a loaf of bread is 24 ounces. By law, the actual weight can vary from the ideal by 1.5 ounces. What range of weight will be acceptable to the inspector without causing the bakery being fined?

Answer: The acceptable weight is 22.5 to 25.5 ounces.

Writing Exercises

61. Write a graphical description of the absolute value of a number

62. In your own words, explain how to solve the absolute value inequality, $|3x−2|\geq 4$.

Answer: Answers will vary.

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$This table has four columns and five rows. The first row is a header and it labels each column, “I can…”, “Confidently,” “With some help,” and “No-I don’t get it!” In row 2, the I can was solve absolute value equations. In row 3, the I can was solve absolute value inequalities with “less than.” In row 4, the I can was solve absolute value inequalities with “greater than.” In row 5, the I can was solve applications with absolute value.$

b. What does this checklist tell you about your mastery of this section? What steps will you take to improve?

Search

Text Color

Text Size

Margin Size

Font Type