1.16: Factoring Trinomials and Mixed Factoring

Factoring Trinomials \(a x^{2}+b x+c\) by the ac-Method

We know that multiplying two binomials by the FOIL method results in a four-term polynomial and in many cases it can be combined into a three-term polynomial. For example:

\[ \begin{align*} (x+3)(2 x+1) &=2 x^{2}+1 x+6 x+3 \\[4pt] &=2 x^{2}+7 x+3 . \end{align*}\]

This indicates that if we want to factor the expression \(2 x^{2}+7 x+3\), we will get a product of two binomials \((x+3)\) and \((2 x+1)\), that is,

\[2 x^{2}+7 x+3=(x+3)(2 x+1). \nonumber\]

In this section, we will learn how to reverse the procedure of FOIL to factor trinomials of the form \(a x^{2}+b x+c \). The procedure is called the ac-Method.

ac-Method to factor \(a x^{2}+b x+c ; a \neq 0\)

• Step 1. Find the product \(a c\), that is the product of the coefficients of the first and last terms.
• Step 2. Find two integers whose product is \(a c\) and whose sum is \(b\). If such an integer pair cannot be found, then the polynomial cannot be factored out.
• Step 3. Use the two integers found in step 2 to rewrite the term \(b x\) as a sum of two terms.
• Step 4. Factor by the grouping method.

For example: Factor \(2 x^{2}+7 x+3\).

Step \(1 \). The product of \(a c\) is \(2 \cdot 3=6\).

Step 2. We look for two numbers whose product is 6 and whose sum is 7 . We can do this by inspection or by writing all pairs of numbers whose product is 6 and calculate the sum for each pair: \(1+6=7,2+3=5\). So 1 and 6 are the numbers we are looking for.

Step 3. We write \(7 x=1 x+6 x\) so

\[2 x^{2}+7 x+3=2 x^{2}+x+6 x+3\nonumber\]

Step 4.

\[\begin{align*}\begin{aligned}
2 x^{2}+x+6 x+3 &=\left(2 x^{2}+x\right)+(6 x+3) ~~ \text{Factor by Grouping} \\
&=x(2 x+1)+3(2 x+1) \\
&=(x+3)(2 x+1)
\end{aligned}\end{align*}\nonumber\]

We can check to see if we factored correctly by distributing our answer. We can use the FOIL method learned previously to check if the factored binomials give us the original trinomial \(2 x^{2}+7 x+3\).

Example \(\PageIndex{1}\)

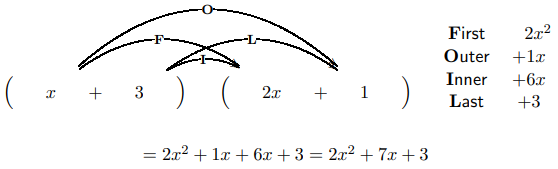
Factor the given polynomial by the ac-Method.

a) \(2 x^{2}+15 x-27\)

• Step 1. The product of \(a c=(2)(-27)=-54\)
• Step 2. Now we need to find two integers whose product is - 54 . We can list all the possibilities:

\[(-1)(54), \quad(-2)(27), \quad(-3)(18), \quad(-6)(9),\nonumber\]

\[(1)(-54), \quad(2)(-27), \quad(3)(-18), \quad(6)(-9)\nonumber\]

and calculate the sum of each pair. Only integers -3 and 18 add up to 15 .

• Step 3. We can rewrite the middle term \(15 x=-3 x+18 x \). So \(2 x^{2}+15 x-\) \(27=2 x^{2}-3 x+18 x-27\)
• Step 4. We factor by grouping.

\[\begin{align*}
2 x^{2}+15 x-27 &=2 x^{2}-3 x+18 x-27 \\
&=\left(2 x^{2}-3 x\right)+(18 x-27) \\
&=x(2 x-3)+9(2 x-3) \\
&=(x+9)(2 x-3)
\end{align*}\nonumber\]

b) \(12 x^{2}-11 x+2:\)

Step 1. The product of \(a c=(12)(2)=24\)

Step 2. We need to find two integers whose product is 24 and whose sum is -11 . We list all pairs of factors of 24:

\[(1)(24), \quad(2)(12), \quad(3)(8), \quad(4)(6)\nonumber\]

\[(-1)(-24), \quad(-2)(-12), \quad(-3)(-8), \quad(-4)(-6)\nonumber\]

The pair -3 and -8 will have a sum -11.

Step 3. We rewrite the middle term \(-11 x=(-3 x)+(-8 x)\).

Step 4. Then we can finish the factoring.

\[\begin{align*}
12 x^{2}-11 x+2 &=12 x^{2}-3 x+(-8 x)+2 \\
&=\left(12 x^{2}-3 x\right)+(-8 x+2) \\
&=3 x(4 x-1)+(-2)(4 x-1) \\
&=(3 x-2)(4 x-1)
\end{align*}\nonumber\]

Note that when we rewrite the middle term, we write it as a sum (even if the second term is negative). This is in order to be able to group without worrying about subtraction. since otherwise the grouping step would look like this:

\[12 x^{2}-3 x-8 x+2=\left(12 x^{2}-3 x\right)-(8 x-2) \nonumber\]

(note the subtraction of 2). Also, note that we factored out (-2) in the second to the last step. This was in order to make sure that \((4 x-1)\) was a common factor.

c) \(3 x^{2}+4 x-2\)

The product of \(a c=(3)(-2)=-6\), and this number factors as:

\[(-1)(6), \quad(-2)(3), \quad(1)(-6), \quad(2)(-3)\nonumber\]

It is clear that none of pairs in the list will give a sum \(4 \). This means that the polynomial \(3 x^{2}+4 x-2\) cannot be factored into two binomials (using integers). We call it a prime polynomial.

Factoring Trinomials \(x^{2}+b x+c\)

In the special case when \(a=1\), the AC-method still works. For example, to factor \(x^{2}-6 x+5\), we first compute \(a c=(1)(5)=5 \). Then we need to find two numbers whose product is 5 and whose sum is \(-6 \). since \((-1)(-5)=5\) and \((-1)+(-5)=-6\), by the grouping method we have:

\[\begin{align*}
x^{2}-6 x+5 &=x^{2}-1 x+(-5 x)+5 \\
&=\left(x^{2}-1 x\right)+(-5 x+5) \\
&=x(x-1)+(-5)(x-1) \\
&=(x-5)(x-1)
\end{align*}\nonumber\]

Now let's observe the result. The result has the form \((x+[-5])(x+[-1])\), and the two numbers in the two boxes are just the two numbers we get to rewrite the coefficient of the middle term \(-6\), that is -1 and \(-5 \).

This example shows that to factor \(x^{2}+b x+c\), the grouping method can be simplified. We can directly write out the factored form of the polynomial once we know the two numbers that multiply to \(a c\) and add to \(b\). In other words, \(x^{2}+b x+c\) is factored as \((x+\square)(x+\square)\), the product of the two numbers in the boxes being \(a c=(1)(c)=c\) and the sum of the two numbers in the boxes being \(b\),

Example 14.2

Factor the given trinomial.

a) \(x^{2}+7 x+10\):

We need to find two numbers whose product is \(a c=c=10\), and whose sum is \(7 \). Number 10 is a product of the following two numbers:

\[(1)(10), \quad(2)(5), \quad(-1)(-10), \quad(-2)(-5)\nonumber\]

The pair 2 and 5 gives a sum \(7\), therefore the trinomial can be factored as:

\[x^{2}+7 x+10=(x+2)(x+5)\nonumber\]

b) \(t^{2}+4 t-12\):

We need to find two numbers whose product is \(a c=c=-12\) whose sum is 4. The number -12 is a product of the following two numbers:

\[(1)(-12), \quad(2)(-6), \quad(3)(-4)\nonumber\]

\[(-1)(12), \quad(-2)(6), \quad(-3)(4).\nonumber\]

The pair -2 and 6 gives a sum \(4\), therefore the trinomial can be factored as:

\[t^{2}+4 t-12=(t+(-2))(t+6)=(t-2)(t+6)\nonumber\]

c) \(x^{2}-3 x-24\):

We need to find two numbers whose product is \(a c=c=-24\) whose sum is -3. The number -24 can be factored as:

\[(1)(-24), \quad(2)(-12), \quad(3)(-8), \quad(4)(-6)\nonumber\]

\[(-1)(24), \quad(-2)(12), \quad(-3)(8), \quad(-4)(6).\nonumber\]

Since none of the pairs in the list adds up to \(-3\), the trinomial cannot be factored as a product of two binomials. This is a prime polynomial.

Mixed Factoring

So far, we have explained the basic techniques of factoring polynomials. Here is the guideline we can follow to select the right method to factor a given polynomial completely.

Guidelines to Factoring a Polynomial Completely

• Step 1. Factor out the GCF from all terms if possible.
• Step 2. Count the number of terms of the polynomial: if the polynomial has two terms, try the formula of difference of two squares; if the polynomial has three terms, try the AC-method; if the polynomial has four terms, try the grouping method.
• Step 3. Check to see if the factors themselves can be factored. If the answer is yes, then factor them completely using the methods in step 2 .

Example 14.3

Factor the given polynomial completely.

a) \(3 x^{2}-12\):

\[\begin{align*}
3 x^{2}-12 &=3\left(x^{2}-4\right) \quad \text { Factor out the GCF 3} \\
&=3(x+2)(x+(-2)) \quad \text { Factor the difference of two squares } x^2-4 \\
&=3(x+2)(x-2)
\end{align*}\nonumber\]

b) \(4 x^{3}-20 x^{2}+24 x\):

\[\begin{align*}
4 x^{3}-20 x^{2}+24 x &=4 x\left(x^{2}-5 x+6\right) \quad \text { Factor out the GCF } 4x \\
&=4 x(x+(-2))(x+(-3)) \quad \text { Factor the trinomial } x^{2}-5 x+6 \\
&=4 x(x-2)(x-3)
\end{align*}\nonumber\]

c) \(-10 z^{2}-4 z+6\):

\[\begin{align*}
-10 z^{2}-4 z+6 &=-2\left(5 z^{2}+2 z-3\right) \quad \text { Factor out the opposite of the GCF } -2 \\
&=-2\left(5 z^{2}-3 z+5 z-3\right) \quad \text { Factor the trinomial } 5 z^{2}+2 z-3 \\
&=-2\left[\left(5 z^{2}-3 z\right)+(5 z-3)\right] \\ &=-2[z(5 z-3)+1(5 z-3)] \\ &=-2(z+1)(5 z-3)
\end{align*}\nonumber\]

d) \(x^{3}-7 x^{2}-4 x+28\)

\[\begin{align*}
x^{3}-7 x^{2}-4 x+28 &=\left(x^{3}-7 x^{2}\right)+(-4 x+28) \quad \text { Factor by grouping } \\
&=x^{2}(x-7)+(-4)(x-7) \\
&=\left(x^{2}-4\right)(x-7) \\ &=(x+2)(x+(-2))(x-7) \quad \text { Factor } x^{2}-4 \\ &=(x+2)(x-2)(x-7)
\end{align*}\nonumber\]

e) \(30 x^{2}+10 x^{4}-280\)

\[\begin{align*}
30 x^{2}+10 x^{4}-280 &=10 x^{4}+30 x^{2}-280 \quad \text { Reorder in decreasing powers of the variable } \\
&=10\left(x^{4}+3 x^{2}-28\right) \quad \text { Factor out the GCF } 10 \\
&=10\left(y^{2}+3 y-28\right) \quad \text { Write } y=x^{2} \text{ to recognize as a quadratic expression} \\ &=10(y+7)(y-4) \\ &=10\left(x^{2}+7\right)\left(x^{2}-4\right) \quad \text { Replace } y \text{ with } x^2 \text{and look to see if anything can be factor out}\\ &= 10\left(x^{2}+7\right)(x+2)(x-2)
\end{align*}\nonumber\]

Exit Problem

Factor completely: \(8 x^{2}-10 x+3\)