1.22: Solving Quadratic Equations by Factoring

As mentioned earlier, solving equations is dependent on the type of equation at hand. You can review solving linear equations in chapter 16. This chapter will deal with solving quadratic equations. These are equations that contain the second power of a variable and nothing higher.

Example 20.1

Examples of quadratic equations:

a) \(x^{2}-3 x-18=0\) is a quadratic equation.

b) \(x^{2}=81\) is a quadratic equation.

c) \(4 x^{2}-36=0\) is a quadratic equation.

d) \(x^{3}-27=0\) is not a quadratic equation, since it includes a third degree variable - we will not discuss solving such equations in this class.

Solving Quadratic Equations

Solving quadratic equations involves three basic steps. We will look at each of these steps as we proceed to solve \(x^{2}=100\).

Step 1. Standard Form

We say that an equation is in standard form if all the terms are collected on one side of the equal sign, and there is only a 0 on the other side. For instance, equations a) and c) in the previous example are quadratic equations in standard form.

If we are working with an equation that is not in standard form, we can easily get it to the desired form by adding or subtracting terms from both sides.

For instance, the equation \(x^{2}=100\) is not in standard form. To get it to standard form, we subtract 100 from both sides of the equation:

\[x^{2}=100\nonumber\]

\[-100 \quad-100\nonumber\]

\[\Longrightarrow x^{2}-100=0\nonumber\]

Note: If the equation at hand is already in standard form, then we skip this step.

Step 2. Factor

Now that all the terms are on one side of the equation, we factor the quadratic expression at hand. It is a good idea to review the factoring techniques introduced in chapters 12, 13 and 14.

\[\begin{align*}
x^{2}-100 &=0 \\
\Longrightarrow x^{2}-(10)^{2} &=0 \\
\Longrightarrow(x-10)(x+10) &=0
\end{align*}\nonumber\]

Step 3. Use the Zero-Product Property

Zero-Product Property

If \(A \cdot B=0\) then \(A=0\) or \(B=0\).

The reason why this property is helpful in solving quadratic equations is because after you have put your equation in standard form and factored, you are exactly in a situation where you can apply the Zero-Product Property.

\[(x-10)(x+10)=0\nonumber\]

translates into:

\[(x-10)=0 \text { or }(x+10)=0\nonumber\]

and now, both of the equations at hand are linear, and solving them is a matter of isolating the variable with some algebraic manipulations. Notice that now you have two linear equations, each will give its own solution. So, your original quadratic equation will have two solutions.

\[x − 10 = 0 \text{ gives }x = 10\nonumber\]

and

\[x + 10 = 0 \text{ gives }x = −10\nonumber\]

So, the solutions of the equation \(x^{2}=100\) are \(x=10\) and \(x=-10\).

Step 4. Check (optional)

It is not mandatory (unless the question specifically asks for it), but it is a good habit to check whether the solutions obtained are correct. To check if our solutions are correct, we need to substitute 10 and -10 into the original equation \(x^{2}=100\).

We easily see that \((10)^{2}=100\) and \((-10)^{2}=100,\) so both solutions work.

Example 20.2

Solve:

a) \(5(x-2)(x+3)=0\)

Notice that this equation is already in standard form and factored. To apply the Zero-Product Property for

\[5(x-2)(x+3)=0\nonumber\]

We first divide both sides of the equation by 5 (or multiply by \(\frac{1}{5}\) ):

\[\frac{5(x-2)(x+3)}{5}=\frac{0}{5}\nonumber\]

This gives

\[(x-2)(x+3)=0\nonumber\]

Now we apply the Zero-Product Property

\[(x-2)=0 \text { or }(x+3)=0\nonumber\]

\[x-2=0 \text{ gives } x=2\nonumber\]

and

\[x + 3 = 0 \text{ gives } x = −3\nonumber\]

So, the solutions of the equation \(5(x-2)(x+3)=0\) are \(x=2\) and \(x=-3\). We can easily check that \(5(x-2)(x+3)\) evaluated at \(x=2\) gives 0 and also at \(x=-3\) gives 0.

b) \((5 x-4)(x-6)=0\)

Notice that this equation is already in standard form and factored, and we can directly apply the Zero-Product Property.

\[(5 x-4)=0 \text { or }(x-6)=0\nonumber\]

\[5 x-4=0 \text{ gives }5x = 4 \text{ and thus }x=\frac{4}{5}\nonumber\]

and

\[x − 6 = 0 \text{ gives } x = 6\nonumber\]

So, the solutions of the equation \((5 x-4)(x-6)=0\) are \(x=\frac{4}{5}\) and \(x=6\).

Example 20.3

Solve the given quadratic equations:

a) \(x^{2}-3 x-18=0\)

This is a quadratic equation in standard form.

\[\begin{array} {ll} \text{Standard Form} & x^{2}-3 x-18=0 \\ \text{Factor} & \Longrightarrow(x-6)(x+3)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-6)=0 \text { or }(x+3)=0 \end{array}\nonumber\]

\[x − 6 = 0 \text{ gives } x = 6\nonumber\]

and

\[x + 3 = 0 \text{ gives } x = −3\nonumber\]

So \(x=6\) or \(x=-3\).

b) \(x^{2}=81\)

This is a quadratic equation not in standard form.

\[\begin{array} {ll} \text{Standard Form} & x^{2}-81=0 \\ \text{Factor} & \Longrightarrow x^{2}-(9)^{2}=0 \\ & \Longrightarrow(x-9)(x+9)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-9)=0 \text { or }(x+9)=0 \end{array}\nonumber\]

\[x − 9 = 0 \text{ gives } x = 9 \nonumber\]

and

\[x + 9 = 0 \text{ gives } x = −9 \nonumber\]

The solutions are \(x=9\) and \(x=-9\).

c) \(3 x^{2}-27=0\)

This is a quadratic equation in standard form.

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}-27=0 \\ \text{Factor} & \Longrightarrow 3 \cdot x^{2}-3 \cdot 9=0 \\ & \Longrightarrow 3\left(x^{2}-9\right)=0 \\ & \Longrightarrow 3\left(x^{2}-3^{2}\right)=0 \\ & \Longrightarrow 3(x-3)(x+3)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-3)=0 \text { or }(x+3)=0 \end{array}\nonumber\]

\[x − 3 = 0 \text{ gives }x = 3 \nonumber\]

and

\[x + 3 = 0 \text{ gives } x = −3 \nonumber\]

The solutions are \(x=3\) and \(x=-3\).

d) \(x^{2}+5 x+4=0\)

\[\begin{array} {ll} \text{Standard Form} & x^{2}+5 x+4=0 \\ \text{Factor} & \Longrightarrow(x+4)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x+4)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x + 4 = 0 \text{ gives } x = −4\nonumber\]

and

\[x + 1 = 0 \text{ gives } x= -1\nonumber\]

So if \(x^{2}+5 x+4=0\) then \(x=-4\) or \(x=-1\).

e) \(x^{2}=7 x\)

\[\begin{array} {ll} \text{Standard Form} & x^{2}-7 x=0 \\ \text{Factor} & \Longrightarrow x \cdot x-7 \cdot x=0 \\ & \Longrightarrow x(x-7)=0 \\ \text{Zero-Product Property} & \Longrightarrow x=0 \text { or }(x-7)=0 \end{array}\nonumber\]

\[x=0 \text{ gives }x=0\nonumber\]

and

\[x-7=0 \text{ gives } x= 7\nonumber\]

The solutions are \(x=0\) and \(x=7\)

f) \(4 x^{2}+20 x=0\)

\[\begin{array} {ll} \text{Standard Form} & 4 x^{2}+20 x=0 \\ \text{Factor} & \Longrightarrow 4 x \cdot x+4 x \cdot 5=0 \\ & \Longrightarrow 4 x(x+5)=0 \\ \text{Zero-Product Property} & \Longrightarrow 4 x=0 \text { or }(x+5)=0 \end{array}\nonumber\]

\[4x = 0 \text{ gives } \frac{4 x}{4}=\frac{0}{4} \text{ thus } x=0\nonumber\]

and

\[x + 5 = 0 \text{ gives } x = −5\nonumber\]

The solutions are \(x=0\) and \(x=-5\).

g) \(4 x^{2}-25=0\)

\[\begin{array} {ll} \text{Standard Form} & 4 x^{2}-25=0 \\ \text{Factor} & \Longrightarrow(2 x)^{2}-(5)^{2}=0 \\ & \Longrightarrow(2 x-5)(2 x+5)=0 \\ \text{Zero-Product Property} & \Longrightarrow(2 x-5)=0 \text { or }(2 x+5)=0 \end{array}\nonumber\]

\[2 x-5=0 \text{ gives } 2 x=5 \text{ thus } x=\frac{5}{2} \nonumber\]

and

\[2 x+5=0 \text{ gives } 2 x=-5 \text{ thus } x=\frac{-5}{2} \nonumber\]

The solutions are \(x=\frac{5}{2}\) or \(x=-\frac{5}{2}\)

h) \(3 x^{2}+7 x+2=0\)

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}+7 x+2=0 \\ \text{Factor} & \Longrightarrow 3 x^{2}+6 x+x+2=0 \\ & \Longrightarrow 3 x \cdot x+3 x \cdot 2+x+2=0 \\ & \Longrightarrow 3 x(x+2)+(x+2)=0 \\ & \Longrightarrow(3 x+1)(x+2)=0 \\ \text{Zero-Product Property} & \Longrightarrow(3 x+1)=0 \text { or }(x+2)=0 \end{array}\nonumber\]

\[3 x+1=0 \text{ gives } 3 x=-1 \text{ thus } x=\frac{-1}{3} \nonumber\]

and

\[x+2=0 \text{ gives } x=-2 \nonumber\]

The solutions are \(x=-\frac{1}{3}\) and \(x=-2\).

i) \(x^{2}=-2 x-1\)

\[\begin{array} {ll} \text{Standard Form} & \Longrightarrow x^{2}+2 x+1=0 \\ \text{Factor} & \Longrightarrow(x+1)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x+1)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x+1=0 \text{ gives } x=-1 \nonumber\]

and

\[x+1=0 \text{ gives } x=-1 \nonumber\]

Since both solutions are the same, we say that we have a double solution \(x=-1\).

j) \(2 x^{2}-32=0\)

\[\begin{array} {ll} \text{Standard Form} & \Longrightarrow 2 x^{2}-32=0 \\ \text{Factor} & \\ \Longrightarrow 2 \cdot x^{2}-2 \cdot 16=0 & \Longrightarrow 2\left(x^{2}-16\right)=0 \\ & \Longrightarrow 2\left(x^{2}-4^{2}\right)=0 \\ & \Longrightarrow 2(x-4)(x+4)=0\\ & \Longrightarrow(x-4)(x+4)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-4)=0 \text { or }(x+4)=0 \end{array}\nonumber\]

\[x-4=0 \text{ gives } x=4 \nonumber\]

and

\[x+4=0 \text{ gives } x=-4 \nonumber\]

The solutions are \(x=4\) and \(x=-4\).

k) \(3 x^{2}-3 x-6=0\)

\[\begin{array} {ll} \text{Standard Form} & 3 x^{2}-3 x-6=0 \\ \text{Factor} & \Longrightarrow 3 \cdot x^{2}-3 \cdot x-3 \cdot 2=0 \\ & \Longrightarrow 3\left(x^{2}-x-2\right)=0 \\ & \Longrightarrow 3(x-2)(x+1)=0 \\ & \Longrightarrow(x-2)(x+1)=0 \\ \text{Zero-Product Property} & \Longrightarrow(x-2)=0 \text { or }(x+1)=0 \end{array}\nonumber\]

\[x-2=0 \text{ gives } x=2 \nonumber\]

and

\[x+1=0 \text{ gives } x=-1 \nonumber\]

The solutions are \(x=2\) and \(x=-1\).

If a rectangle has area 15 square feet and its length is two feet less than its width then what are the dimensions of the rectangle.

Let \(x\) represent the width. Then the length is \(x-2\). The area, on the one hand is 15 square feet, and on the other hand is \(l \times w.\) So

\[15=x(x-2)\nonumber\]

We first distribute to get

\[15=x^{2}-2 x\nonumber\]

Now we put it in standard form by subtracting 15 from both sides:

\[x^{2}-2 x-15=0\nonumber\]

Now we factor so that we can use the Zero-Product Property:

\[(x-5)(x+3)=0\nonumber\]

Then \(x-5=0\) or \(x+3=0,\) which gives that \(x=5\) or \(x=-3 .\) But \(x\) is the width of a rectangle and therefore it can not be negative. The only solution to this problem is \(x=5\) (and \(x-2=3\) ). So the dimensions of the rectangle are 5 feet by 3 feet.

Solving Quadratic Equations Of The Form \(x^2 = A\)

In the special case when a quadratic equation is of the form \(x^{2}=A\), we can resort to a short-cut to solve it. Be aware that this short-cut only works in this special case.

We first note that if \(x^{2}=9\) then, by inspection, the solutions are 3 and -3 We see that in general to solve \(x^{2}=A,\) we see that the solutions are \(x=\sqrt{A}\) and \(x=-\sqrt{A}\).

Notice that if we use the factoring method, the equation \(x^{2}=A\) becomes \(x^{2}-A=0\) in standard form, and the factored form of the equation is \((x-\) \(\sqrt{A})(x+\sqrt{A})=0\) which gives the solutions \(x=\sqrt{A}\) and \(x=-\sqrt{A}\).

Example 20.4

Use the shortcut above to solve the given special quadratic equation:

a) \(x^{2}=100\)

Step 1. \(\sqrt{100}=10\)

Step 2. The solutions are \(x=10\) and \(x=-10\)

b) \(x^{2}=72\)

Step 1. \(\sqrt{72}=6 \sqrt{2}\)

Step 2. The solutions are \(x=6 \sqrt{2}\) and \(x=-6 \sqrt{2}\)

c) \(x^{2}-75=0\)

Step 1. \(\sqrt{75}=5 \sqrt{3}\)

Step 2. The solutions are \(x=5 \sqrt{3}\) and \(x=-5 \sqrt{3}\)

d) The area of a square is 20 square feet. How long is each side?

Let \(x\) be the length of each side. Then \(x^{2}=20 .\) So \(x=\sqrt{20}=2 \sqrt{5} .\) Note that it can not be \(-2 \sqrt{5}\) since \(x\) is a length. Each side is \(2 \sqrt{5}\) ft.

Application to the Pythagorean Theorem

The Pythagorean Theorem relates the lengths of the legs of a right triangle and the hypotenuse.

The Pythagorean Theorem: If \(a\) and \(b\) are the lengths of the legs of the right triangle and \(c\) is the length of the hypotenuse (the side opposite the right angle) as seen in this figure,

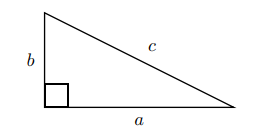
then

\[a^{2}+b^{2}=c^{2}\nonumber\]

Remark 20.5

In the theorem a and b are interchangeable.

Example 20.6

Consider the following right triangle.

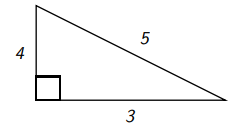
It satisfies the conclusion of the Pythagorean Theorem since \(3^{2}+4^{2}=5^{2}\) (check it).

Remark 20.7

Do not take the proportions of the triangles drawn seriously– what appears to be the shortest leg may not in fact be. These drawings are just cartoons that exhibit a relationship between the legs as they relate to the angles.

If we know any two sides of a right triangle we can find the third using the Pythagorean Theorem. We will look at a few examples.

Example 20.8

Find \(x\) if

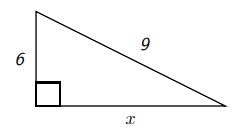
By the Pythagorean Theorem (noting that the length of the hypotenuse is 9 and so 81 belongs on one side of the equality)

\[x^{2}+6^{2}=9^{2} \text{, or equivalently ,} x^{2}+36=81 \nonumber\]

so that

\[x^{2}=81-36 \text{, or equivalently ,} x^{2}=45 \nonumber\]

Now since \(x\) represents a length, it is positive so that

\[x=\sqrt{45}=\sqrt{9 \cdot 5}=3 \sqrt{5}\nonumber\]

Example 20.9

Find \(x\) given the following picture

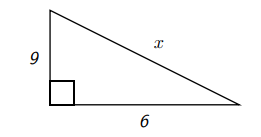
By the Pythagorean Theorem (noting that the length of the hypotenuse is \(x\) and so \(x^{2}\) belongs on one side of the equality)

\[6^{2}+9^{2}=x^{2} \text{, or equivalently ,} 36+81=x^{2} \nonumber\]

so that

\[ x^{2}=117 \nonumber\]

Now since \(x\) represents a length, it is positive so that

\[ x=\sqrt{117}=\sqrt{9 \cdot 13}=3 \sqrt{13} \nonumber\]

Example 20.10

Suppose you must reach a window of a house with a ladder so that the ladder meets the house 7 ft off the ground. Suppose also that the ladder must be 5 ft from the base of the house. How long must the ladder be?

This information leads to the triangle (not drawn to scale):

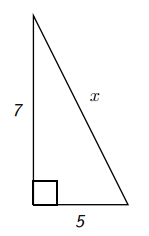
So by the Pythagorean Theorem says

\[ 5^{2}+7^{2}=x^{2} \nonumber\]

so that \(x^{2}=74\). Therefore the ladder must be \(\sqrt{74}\) ft long which is approximately 8.6 ft long.

Exit Problem

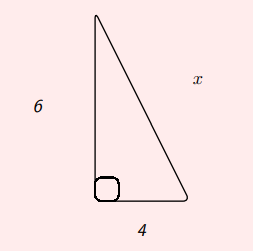1. Solve: \(x^{2}-5 x=6\)
2. Solve: \(16 x^{2}=81\)
3. Solve: \(-24 x=10 x^{2}\)
4. Solve for \(x\) in the given right triangle.