1.23: Linear Inequalities

Last updated
Save as PDF

Page ID: 47196

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In this section we solve linear inequalities.

Consider the inequality $2 x-1>2$. To solve this means to find all values of $x$ that satisfy the inequality (so that when you plug in those values for $x$ you get a true statement). For example, since $2 \cdot 5-1=9>2, x=5$ is a solution and since $2 \cdot 1-1=1 \not>2, x=1$ is not a solution.

We can solve an inequality in much the same way as we solve an equality with one important exception:

Multiplication or division by a negative number reverses the direction of the inequality.

For example $-3 x>9 \Longleftrightarrow \frac{-3 x}{-3}<\frac{9}{-3} \Longleftrightarrow x<-3$. We see that
$x=-10$ satisfies all of these inequalities and $x=3$ satisfies none of them. We can graph the solution on the number line:

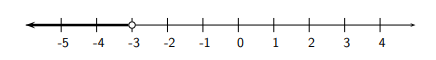
$clipboard_efcf6d3b0ad32a277fc29febc7bb7b300.png$

But $3 x>9 \Longleftrightarrow \frac{3 x}{3}>\frac{9}{3} \Longleftrightarrow x>3$.

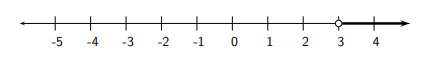
$clipboard_e9e89fc9579852b60b5f6e6178e374fb3.png$

For instance, check that $x=5$ (which is greater than 3 ) satisfies the inequality.

Example 21.1

Solve the given inequality and represent the solution on the number line:

a) $5 x>10 \Longleftrightarrow x>\frac{10}{5} \Longleftrightarrow x>2$

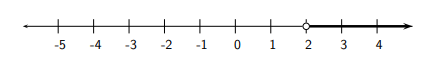
$clipboard_e69bd65626bef756f24bbc854e38b6c09.png$

b) $-10 x \leq-5 \Longleftrightarrow x \geq \frac{-5}{-10} \Longleftrightarrow x \geq \frac{1}{2}$

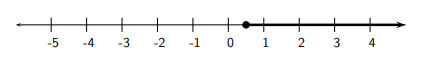
$clipboard_e7ff97fb7d1a502850f6e7b0287250818.png$

c) $-x>-2 \Longleftrightarrow x<\frac{-2}{-1} \Longleftrightarrow x<2$

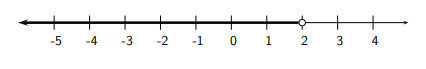
$clipboard_e7f49abafa8b8e3e3af1aedd9c203fd09.png$

d) $2-x \geq 2 x-5 \Longleftrightarrow 7-x \geq 2 x \Longleftrightarrow 7 \geq 3 x \Longleftrightarrow \frac{7}{3} \geq x$ (or $\left.x \leq \frac{7}{3}\right)$

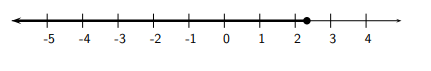
$clipboard_e21cf36535d9db45e14f0bb3ff0501b95.png$

e) $2-3 x \geq-2 x+7 \Longleftrightarrow-5-3 x \geq-2 x \Longleftrightarrow-5 \geq x$ (or $x \leq-5)$

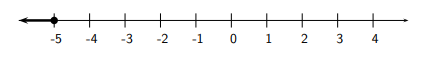
$clipboard_ed53e5a20ed016342e96b6f880306a6dd.png$

f) $3(x-2)+5 \leq 5-2(x+1) \Longleftrightarrow 3 x-6+5 \leq 5-2 x-2 \Longleftrightarrow 3 x-1 \leq 3-2 x \Longleftrightarrow 3 x+2 x \leq 3+1 \Longleftrightarrow 5 x \leq 4 \Longleftrightarrow x \leq \frac{4}{5}$

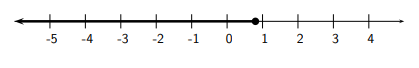
$clipboard_e29e83f963ad9cd4628ed09fdf1862a6b.png$

Note: There is more than one way to do a problem. For example:

$-3 x-2<1 \Longleftrightarrow-3 x<2+1 \Longleftrightarrow-3 x<3 \Longleftrightarrow \frac{-3 x}{-3}>\frac{3}{-3} \Longleftrightarrow x>-1 $

or,

$-3 x-2<1 \Longleftrightarrow-2<1+3 x \Longleftrightarrow-2-1<3 x \Longleftrightarrow-3<3 x \Longleftrightarrow-1<x($ which is the same as $x>-1)$

$clipboard_e4daab39e5a4895d73f78c497943d4913.png$

Exit Problem

Solve the inequality and show the graph of the solution:

\[7 x+4 \leq 2 x-6\nonumber\]