1.5: Multiply and Divide Integers
- Page ID
- 15120
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Multiply integers
- Divide integers
- Simplify expressions with integers
- Evaluate variable expressions with integers
- Translate English phrases to algebraic expressions
- Use integers in applications
A more thorough introduction to the topics covered in this section can be found in the Prealgebra chapter, Integers.
Multiply Integers
Since multiplication is mathematical shorthand for repeated addition, our model can easily be applied to show multiplication of integers. Let’s look at this concrete model to see what patterns we notice. We will use the same examples that we used for addition and subtraction. Here, we will use the model just to help us discover the pattern.
We remember that \(a\cdot b\) means add \(a,\, b\) times. Here, we are using the model just to help us discover the pattern.
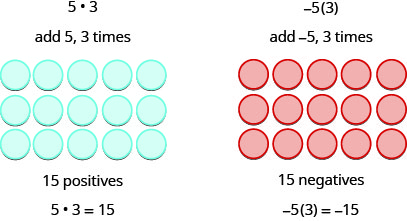
The next two examples are more interesting.
What does it mean to multiply \(5\) by \(−3\)? It means subtract \(5, 3\) times. Looking at subtraction as “taking away,” it means to take away \(5, 3\) times. But there is nothing to take away, so we start by adding neutral pairs on the workspace. Then we take away \(5\) three times.
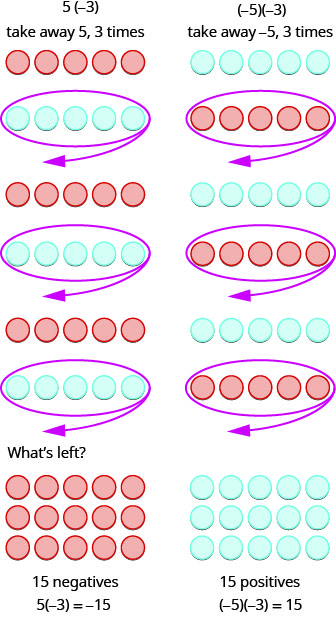
In summary:
\[\begin{array} {ll} {5 \cdot 3 = 15} &{-5(3) = -15} \\ {5(-3) = -15} &{(-5)(-3) = 15} \end{array} \nonumber\]
Notice that for multiplication of two signed numbers, when the:
- signs are the same, the product is positive.
- signs are different, the product is negative.
We’ll put this all together in the chart below.
For multiplication of two signed numbers:
| Same signs | Product | Example |
|---|---|---|
| Two positives | Positive | \(7\cdot 4 = 28\) |
| Two negatives | Positive | \(-8(-6) = 48\) |
| Different signs | Product | Example |
|---|---|---|
| Positive \(\cdot\) negative | Negative | \(7(-9) = -63\) |
| Negative \(\cdot\) positive | Negative | \(-5\cdot 10= -50\) |
Multiply:
- \(-9\cdot 3\)
- \(-2(-5)\)
- \(4(-8)\)
- \(7\cdot 6\)
Solution
- \(-9\cdot 3 = -27 \quad \text{Multiply, noting that the signs are different, so the product is negative.}\)
- \( -2(-5) = 10 \quad \text{Multiply, noting that the signs are same, so the product is positive.}\)
- \( \quad 4(-8) = -32 \quad \text{Multiply, with different signs.} \)
- \( \quad 7\cdot 6 = 42 \quad \text{Multiply, with the same signs.} \)
Multiply:
- \(-6\cdot 8\)
- \(-4(-7)\)
- \(9(-7)\)
- \(5\cdot 12\)
- Answer
-
- \(-48\)
- \(28\)
- \(-63\)
- \(60\)
Multiply:
- \(-8\cdot 7\)
- \(-6(-9)\)
- \(7(-4)\)
- \(3\cdot 13\)
- Answer
-
- \(-56\)
- \(54\)
- \(-28\)
- \(39\)
When we multiply a number by \(1\), the result is the same number. What happens when we multiply a number by \(−1\)? Let’s multiply a positive number and then a negative number by \(−1\) to see what we get.
\[\begin{array} {ll} {\text{Multiply.}} & {\text{Multiply.}} \\ {-1\cdot 4 = -4} & {-1(-3)= 3} \\ {} & {} \\ {\text{Note that } -4\text{ is the opposite of 4.}} & {\text{Note that }3\text{ is the opposite of } -3} \end{array} \nonumber\]
Each time we multiply a number by \(−1\), we get its opposite!
\[−1a=−a \nonumber\]
Multiplying a number by \(−1\) gives its opposite.
Multiply:
- \(-1 \cdot 7\)
- \(-1(-11)\)
Solution
- \[\begin{array} {ll} {} &{-1\cdot 7} \\ {\text{Multiply, noting that the signs are different}} &{-7} \\ {\text{so the product is negative.}} &{-7\text{ is the opposite of 7.}} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &{-1(-11)} \\ {\text{Multiply, noting that the signs are the same}} &{11} \\ {\text{so the product is positive.}} &{11\text{ is the opposite of -11.}} \end{array} \nonumber\]
Multiply:
- \(-1\cdot 9\)
- \(-1\cdot(-17)\)
- Answer
-
- \(-9\)
- \(17\)
Multiply:
- \(-1\cdot 8\)
- \(-1\cdot(-16)\)
- Answer
-
- \(-8\)
- \(16\)
Divide Integers
What about division? Division is the inverse operation of multiplication. So, \(15\div 3=5\) because \(5 \cdot 3 = 15\). In words, this expression says that \(15\) can be divided into three groups of five each because adding five three times gives \(15\). Look at some examples of multiplying integers, to figure out the rules for dividing integers.
\[ \begin{align*} 5 \cdot 3 &= 15 & \text{so} & & 15 \div 3 &= 5 \\
-5 \cdot 3 &= -15 & \text{so} & & -15 \div 3 &= -5 \\
(5)(-3) &= -15 & \text{so} & & -15 \div (-3) &= 5 \\
(-5)(-3) &= 15 & \text{so} & & 15 \div (-3) &= -5 \end{align*} \]
Division follows the same rules as multiplication!
For division of two signed numbers, when the:
- signs are the same, the quotient is positive.
- signs are different, the quotient is negative.
And remember that we can always check the answer of a division problem by multiplying.
For multiplication and division of two signed numbers:
- If the signs are the same, the result is positive.
- If the signs are different, the result is negative.
| Same signs | Result |
|---|---|
| Two positives | Positive |
| Two negatives | Positive |
| If the signs are the same, the result is positive. | |
| Different signs | Result |
|---|---|
| Positive and negative | Negative |
| Negative and positive | Negative |
| If the signs are different, the result is negative. | |
- \(-27\div 3\)
- \(-100\div (-4)\)
Solution
- \[\begin{array} {ll} {} &{-27 \div 3} \\ {\text{Divide, with different signs, the quotient is}} &{-9} \\ {\text{negative.}} &{} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &{-100 \div (-4)} \\ {\text{Divide, with signs that are the same the}} &{25} \\ {\text{ quotient is negative.}} &{} \end{array} \nonumber\]
Divide:
- \(-42\div 6\)
- \(-117\div (-3)\)
- Answer
-
- \(-7\)
- \(39\)
Divide:
- \(-63\div 7\)
- \(-115\div (-5)\)
- Answer
-
- \(-9\)
- \(23\)
Simplify Expressions with Integers
What happens when there are more than two numbers in an expression? The order of operations still applies when negatives are included. Remember My Dear Aunt Sally?
Let’s try some examples. We’ll simplify expressions that use all four operations with integers—addition, subtraction, multiplication, and division. Remember to follow the order of operations.
Simplify:
\(7(-2)+4(-7)-6\)
Solution
\[\begin{array} {ll} {} &{7(-2)+4(-7)-6} \\ {\text{Multiply first.}} &{-14+(-28)-6} \\ {\text{Add.}} &{-42-6} \\{\text{Subtract}} &{-48} \end{array} \nonumber\]
Simplify:
\(8(-3)+5(-7)-4\)
- Answer
-
\(-63\)
Simplify:
\(9(-3)+7(-8)-1\)
- Answer
-
\(-84\)
Simplify:
- \((-2)^{4}\)
- \(-2^{4}\)
Solution
- \[\begin{array} {ll} {} &{(-2)^{4}} \\ {\text{Write in expanded form.}} &{(-2)(-2)(-2)(-2)} \\ {\text{Multiply}} &{4(-2)(-2)} \\{\text{Multiply}} &{-8(-2)} \\{\text{Multiply}} &{16} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &{-2^{4}} \\ {\text{Write in expanded form. We are asked to find the opposite of }2^{4}.} &{-(2\cdot 2\cdot 2 \cdot 2)} \\ {\text{Multiply}} &{-(4\cdot 2\cdot 2)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Multiply}} &{-16} \end{array} \nonumber\]
Notice the difference in parts (1) and (2). In part (1), the exponent means to raise what is in the parentheses, the \((−2)\) to the \(4^{th}\) power. In part (2), the exponent means to raise just the \(2\) to the \(4^{th}\) power and then take the opposite.
Simplify:
- \((-3)^{4}\)
- \(-3^{4}\)
- Answer
-
- \(81\)
- \(-81\)
Simplify:
- \((-7)^{2}\)
- \(-7^{2}\)
- Answer
-
- \(49\)
- \(-49\)
The next example reminds us to simplify inside parentheses first.
Simplify:
\(12-3(9 - 12)\)
Solution
\[\begin{array} {llll} {12-3(9 - 12)} & {}\\ {= 12-3(-3)} & {\text{Subtract in parentheses first.}}\\ {= 12-(-9)} & {\text{Multiply.}}\\ {= 12 + 9} & {\text{Add the opposite.}} \\ {=21} & {}\end{array} \nonumber\]
Simplify:
\(17 - 4(8 - 11)\)
- Answer
-
\(29\)
Simplify:
\(16 - 6(7 - 13)\)
- Answer
-
\(52\)
Simplify:
\(8(-9)\div (-2)^{3}\)
Solution
\[\begin{array} {ll} {} &{8(-9)\div(-2)^{3}} \\ {\text{Exponents first}} &{8(-9)\div(-8)} \\ {\text{Multiply.}} &{-72\div (-8)} \\{\text{Divide}} &{9} \end{array} \nonumber\]
Simplify:
\(12(-9)\div (-3)^{3}\)
- Answer
-
\(4\)
Simplify:
\(18(-4)\div (-2)^{3}\)
- Answer
-
\(9\)
Simplify:
\(-30\div 2 + (-3)(-7)\)
Solution
\[\begin{array} {ll} {} &{-30\div 2 + (-3)(-7)} \\ {\text{Multiply and divide left to right, so divide first.}} &{-15+(-3)(-7)} \\ {\text{Multiply.}} &{-15+ 21} \\{\text{Add}} &{6} \end{array} \nonumber\]
Simplify:
\(-27\div 3 + (-5)(-6)\)
- Answer
-
\(21\)
Simplify:
\(-32\div 4 + (-2)(-7)\)
- Answer
-
\(6\)
Evaluate Variable Expressions with Integers
Remember that to evaluate an expression means to substitute a number for the variable in the expression. Now we can use negative numbers as well as positive numbers.
When \(n=−5\), evaluate:
- \(n+1\)
- \(−n+1\).
Solution
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute }{ \color{red}{-5}}\text{ for } n} &{\color{red}{-5}}+1 \\ {\text{Simplify.}} &{-4} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute }{ \color{red}{-5}}\text{ for } n} &{- {\color{red}{(-5)}} +1} \\ {\text{Simplify.}} &{5+1} \\{\text{Add.}} &{6} \end{array} \nonumber\]
When \(n=−8\), evaluate:
- \(n+2\)
- \(−n+2\).
- Answer
-
- \(-6\)
- \(10\)
When \(y=−9\), evaluate:
- \(y+8\)
- \(−y+8\).
- Answer
-
- \(-1\)
- \(17\)
Evaluate \((x+y)^{2}\) when \(x = -18\) and \(y = 24\).
Solution
\[\begin{array} {ll} {} &{(x+y)^{2}} \\ {\text{Substitute }-18\text{ for }x \text{ and } 24 \text{ for } y} &{(-18 + 24)^{2}} \\ {\text{Add inside parentheses}} &{(6)^{2}} \\{\text{Simplify.}} &{36} \end{array} \nonumber\]
Evaluate \((x+y)^{2}\) when \(x = -15\) and \(y = 29\).
- Answer
-
\(196\)
Evaluate \((x+y)^{3}\) when \(x = -8\) and \(y = 10\).
- Answer
-
\(8\)
Evaluate \(20 -z \) when
- \(z = 12\)
- \(z = -12\)
Solution
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }12\text{ for }z.} &{20 - 12} \\ {\text{Subtract}} &{8} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }-12\text{ for }z.} &{20 - (-12)} \\ {\text{Subtract}} &{32} \end{array} \nonumber\]
Evaluate \(17 - k\) when
- \(k = 19\)
- \(k = -19\)
- Answer
-
- \(-2\)
- \(36\)
Evaluate \(-5 - b\) when
- \(b = 14\)
- \(b = -14\)
- Answer
-
- \(-19\)
- \(9\)
Evaluate:
\(2x^{2} + 3x + 8\) when \(x = 4\).
Solution
Substitute \(4\) for \(x\). Use parentheses to show multiplication.
\[\begin{array} {ll} {} &{2x^{2} + 3x + 8} \\ {\text{Substitute }} &{2(4)^{2} + 3(4) + 8} \\ {\text{Evaluate exponents.}} &{2(16) + 3(4) + 8} \\ {\text{Multiply.}} &{32 + 12 + 8} \\{\text{Add.}} &{52} \end{array} \nonumber\]
Evaluate:
\(3x^{2} - 2x + 6\) when \(x =-3\).
- Answer
-
\(39\)
Evaluate:
\(4x^{2} - x - 5\) when \(x = -2\).
- Answer
-
\(13\)
Translate Phrases to Expressions with Integers
Our earlier work translating English to algebra also applies to phrases that include both positive and negative numbers.
Translate and simplify: the sum of \(8\) and \(−12\), increased by \(3\).
Solution
\[\begin{array} {ll} {} &{\text{the } \textbf{sum} \text{of 8 and -12, increased by 3}} \\ {\text{Translate.}} &{[8 + (-12)] + 3} \\ {\text{Simplify. Be careful not to confuse the}} &{(-4) + 3} \\{\text{brackets with an absolute value sign.}} \\{\text{Add.}} &{-1} \end{array} \nonumber\]
Translate and simplify: the sum of \(9\) and \(−16\), increased by \(4\).
- Answer
-
\((9 + (-16)) + 4 - 3\)
Translate and simplify: the sum of \(-8\) and \(−12\), increased by \(7\).
- Answer
-
\((-8 + (-12)) + 7 - 13\)
When we first introduced the operation symbols, we saw that the expression may be read in several ways. They are listed in the chart below.
| \(a−b\) |
|---|
| \(a\) minus \(b\) the difference of \(a\) and \(b\) \(b\) subtracted from \(a\) \(b\) less than \(a\) |
Be careful to get a and b in the right order!
Translate and then simplify
- the difference of \(13\) and \(−21\)
- subtract \(24\) from \(−19\).
Solution
- \[\begin{array} {ll} {} &{\text{the } \textbf{difference } \text{of 13 and -21}} \\ {\text{Translate.}} &{13 - (-21)} \\ {\text{Simplify.}} &{34} \end{array} \nonumber\]
- \[\begin{array} {ll} {} &\textbf{subtract }24 \textbf{ from }-19 \\ {\text{Translate.}} &{-19 - 24} \\ {\text{Remember, subtract b from a means }a - b} &{} \\{\text{Simplify.}} &{-43} \end{array} \nonumber\]
Translate and simplify
- the difference of \(14\) and \(−23\)
- subtract \(21\) from \(−17\).
- Answer
-
- \(14 - (-23); 37\)
- \(-17 - 21; -38\)
Translate and simplify
- the difference of \(11\) and \(−19\)
- subtract \(18\) from \(−11\).
- Answer
-
- \(11 - (-19); 30\)
- \(-11 - 18; -29\)
Once again, our prior work translating English to algebra transfers to phrases that include both multiplying and dividing integers. Remember that the key word for multiplication is “product” and for division is “quotient.”
Translate to an algebraic expression and simplify if possible: the product of \(−2\) and \(14\).
Solution
\[\begin{array} {ll} {} &{\text{the product of }-2 \text{ and } 14} \\ {\text{Translate.}} &{(-2)(14)} \\{\text{Simplify.}} &{-28} \end{array} \nonumber\]
Translate to an algebraic expression and simplify if possible: the product of \(−5\) and \(12\).
- Answer
-
\(-5(12); -60\)
Translate to an algebraic expression and simplify if possible: the product of \(8\) and \(-13\).
- Answer
-
\(-8(13); -104\)
Translate to an algebraic expression and simplify if possible: the quotient of \(−56\) and \(−7\).
Solution
\[\begin{array} {ll} {} &{\text{the quotient of }-56 \text{ and } -7} \\ {\text{Translate.}} &{-56\div(-7)} \\{\text{Simplify.}} &{8} \end{array}\]
Translate to an algebraic expression and simplify if possible: the quotient of \(−63\) and \(−9\).
- Answer
-
\(-63\div (-9); 7\)
Translate to an algebraic expression and simplify if possible: the quotient of \(−72\) and \(−9\).
- Answer
-
\(-72\div (-9); 8\)
Use Integers in Applications
We’ll outline a plan to solve applications. It’s hard to find something if we don’t know what we’re looking for or what to call it! So when we solve an application, we first need to determine what the problem is asking us to find. Then we’ll write a phrase that gives the information to find it. We’ll translate the phrase into an expression and then simplify the expression to get the answer. Finally, we summarize the answer in a sentence to make sure it makes sense.
How to Apply a Strategy to Solve Applications with Integers
The temperature in Urbana, Illinois one morning was \(11\) degrees. By mid-afternoon, the temperature had dropped to \(−9\) degrees. What was the difference of the morning and afternoon temperatures?
Solution
| Step 1. Read the problem. Make sure all the words and ideas are understood. | |
| Step 2. Identify what we are asked to find. | the difference of the morning and afternoon temperatures |
| Step 3. Write a phrase that gives the information to find it. | the difference of \(11\) and \(-9\) |
| Step 4. Translate the phrase to an expression. | \(11 - (-9)\) |
| Step 5. Simplify the expression. | \(20\) |
| Step 6. Write a complete sentence that answers the question. | The difference in temperatures was 20 degrees. |
The temperature in Anchorage, Alaska one morning was \(15\) degrees. By mid-afternoon the temperature had dropped to \(30\) degrees below zero. What was the difference in the morning and afternoon temperatures?
- Answer
-
The difference in temperatures was \(45\) degrees.
The temperature in Denver was \(−6\) degrees at lunchtime. By sunset the temperature had dropped to \(−15\) degrees. What was the difference in the lunchtime and sunset temperatures?
- Answer
-
The difference in temperatures was \(9\) degrees.
- Read the problem. Make sure all the words and ideas are understood
- Identify what we are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.
The Mustangs football team received three penalties in the third quarter. Each penalty gave them a loss of fifteen yards. What is the number of yards lost?
Solution
| Step 1. Read the problem. Make sure all the words and ideas are understood. | |
| Step 2. Identify what we are asked to find. | the number of yards lost |
| Step 3. Write a phrase that gives the information to find it. | three times a \(15\)-yard penalty |
| Step 4. Translate the phrase to an expression. | \(3(-15)\) |
| Step 5. Simplify the expression. | \(-45\) |
| Step 6. Write a complete sentence that answers the question. | The team lost \(45\) yards. |
The Bears played poorly and had seven penalties in the game. Each penalty resulted in a loss of \(15\) yards. What is the number of yards lost due to penalties?
- Answer
-
The Bears lost \(105\) yards.
Bill uses the ATM on campus because it is convenient. However, each time he uses it he is charged a $2 fee. Last month he used the ATM eight times. How much was his total fee for using the ATM?
- Answer
-
A $16 fee was deducted from his checking account.
Key Concepts
- Multiplication and Division of Two Signed Numbers
- Same signs—Product is positive
- Different signs—Product is negative
- Strategy for Applications
- Identify what you are asked to find.
- Write a phrase that gives the information to find it.
- Translate the phrase to an expression.
- Simplify the expression.
- Answer the question with a complete sentence.


